闪存控制器中BCH编解码器设计和验证

殷 民， 易 波

(中国科学技术大学 微电子与固体电子实验室，安徽 合肥230001)

0 引言

随着生产工艺的进步和诸如智能手机平板电脑、SSD等消费电子市场对高密度非易失性存储的需求，MLC代替 SLC成为闪存市场的主流趋势。与此同时，MLC伴随的多比特随机错误，对系统的数据可靠性提出新的挑战，例如美光(Micron)的MT29F32G08CBABA系列要求每 540 Byte有 12 bit的纠错能力。SLC中常用的 SEC-DEC编解码已经不再适用，新一代的闪存控制器需要使用纠错能力更强大的BCH编解码。

BCH码取自Bose、Ray-Chaudhuri与 Hocquenghem的缩写，是编码理论尤其是纠错码中研究得比较多的一种编码方法，它的代数结构优美，硬件实现简单，广泛应用于通信行业和信息存储。BCH的解码过程通常分为伴随子计算、关键方程求解、钱搜索验根这3个部分，在众多关键方程求解算法中，简化伯利坎普-梅西算法最为有效。

虽然很多文献中分别实现了闪存控制的BCH编解码，不过这些大多不适合当前闪存控制器，主要原因是，纠错能力太低,不符合闪存芯片的要求。例如文献[1-4]分别实现 4 bit/512 Byte、8 bit/512 Byte、2 bit/21 bit、4 bit/223 bit的纠错能力，远远低于美光系列每540 Byte/12 bit纠错要求。另外，关键方程算法实现主要是欧几里德方法，或是最初的 iBM，无论是从面积还是译码延迟考虑，这些算法并不是最优的算法。本设计中还对码长作了灵活的配置，提供几种可选的码率，只需要在钱搜索中做简单地修改。码长灵活配置是由于软件算法实现的时候，希望把某些关键数据存储在闪存的剩余空间，这些关键数据也希望和普通的数据一样受到ECC的保护，而这些数据长度较短，不同于主要数据部分。具体实现时只需要在钱搜索中做相应的修改。

本设计实现8 bit并行编解码，每1 024 Byte能纠正32 bit的随机错误，冗余位56 Byte，可以应用于美光MT29F32G08CBABA等系列。

1 并行编码器

并行编解码虽然提高硬件复杂度，但能够降低系统工作频率，提高数据带宽。8 bit的并行编解码非常适合闪存应用。作为循环码，BCH(n, k)的码字由生成多项式决定，并且可以写成系统模式，也就是说，码字是通过原始消息和冗余效验位级联组成。BCH的码字u(x)是由生成多项式决定的：

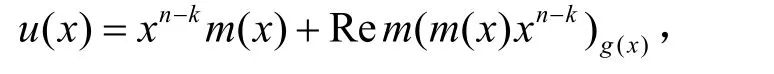
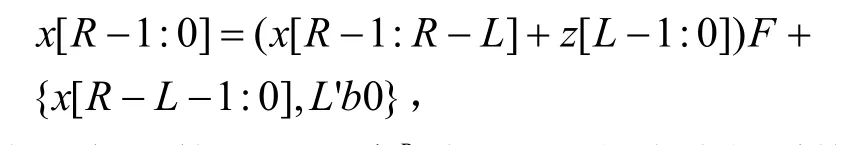
反馈矩阵F第i行是xi+R除以 g(x)的余式的系数，也就是说，高比特的系数移位后，超过 g(x)次数，对低比特产生影响。电路实现如图1所示。

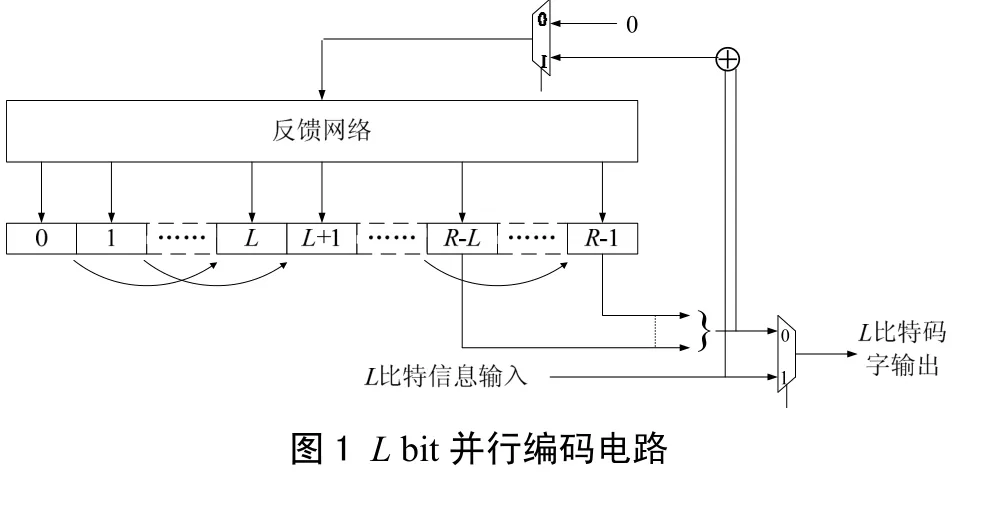
2 并行伴随子生成电路

BCH译码的第一步是计算接收向量的伴随子，伴随子的计算和编码过程非常相似。对接收向量r(x)，有：

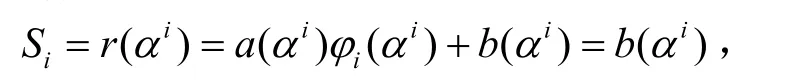
式中，φi(x)是以αi为根的最小多项式，这样，求伴随子的过程就转为求余式b(x)，然后再代入αi，得到伴随子。该做法好处是，在伽罗华域 GF(2M)中，αi, αj(i=j 2l)的最小多项式相同，对应余式b(x)也就相同，这样可以复用求余式 b(x)部分逻辑。将编码过程中生成多项式g(x)换成φi(x)，并注意到输入是从左边进入反馈移位寄存器的，就得到伴随子生成电路，图2是一个φi(x)的求余过程和相应伴随子计算电路。

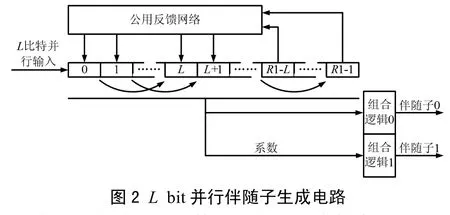
此外，伴随子的计算电路也可以直接实现

S=rαi(n-1)+rαi(n-2)+ ···+rαi+r，

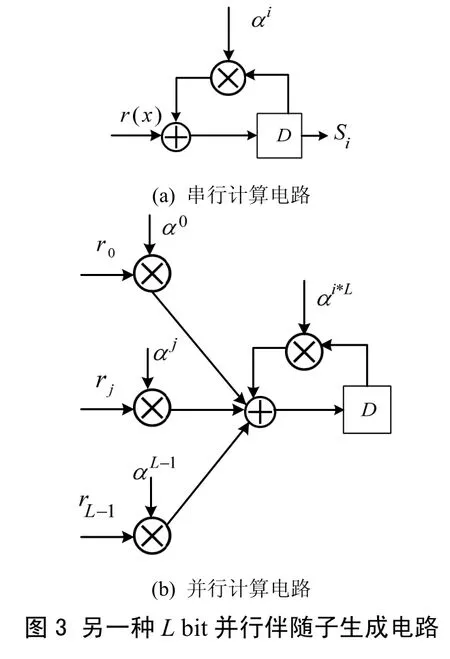
in-1n-210这样不难得到串行伴随子计算电路和并行的伴随子计算电路如图3所示。图3(a)是串行的伴随子计算电路，图3(b)是并行的伴随子计算电路。

3 关键方程

关键方程S( x)Λ(x)=Ω(x)modx2t解法很多，主要算法比较如表1所示。

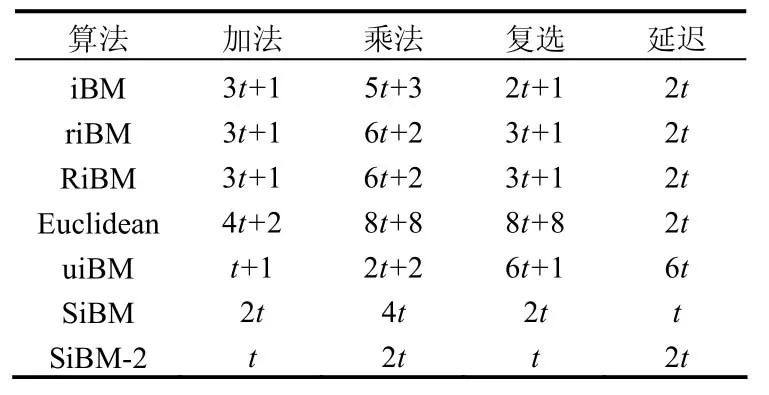
表1 主要算法比较

文献[5]中SiBM算法是文献[6]中RiBM算法在2进制 BCH码上的优化，优化包括两个方面，一是奇次迭代差异为零,可以忽略奇次迭代,二是没有必要计算错误多项式Ω(x)的系数。SiBM-2是采用Folding结构，分时复用逻辑，所以它的逻辑几乎是SiBM算法的一半，但译码的延迟变为两倍。在这里的设计中，更关注译码的延迟对系统性能的改善，而不是面积上的考虑，所以采用SiBM算法。算法伪码如下所示：

Initialization:

在该算法中，涉及到伽罗华域 GF(2M)乘法运算。乘法器可以通过线性反馈移位寄存器实现，作为时序逻辑，虽然面积最优，不过会增加M个时钟延迟，也可以通过组合逻辑实现。在这里的设计中，采用文献[7]中的乘法器设计，该设计将有限域上乘法运算分为普通乘法运算网络和反馈网络，并在面积和延迟上权衡，延迟数量级O(lb(M))。

在SIBM算法电路实现上，首先是定义最小处理单元，它是用来计算下次迭代的θ, δ值。最小处理单元实现和SIBM算法实现电路如图4所示。

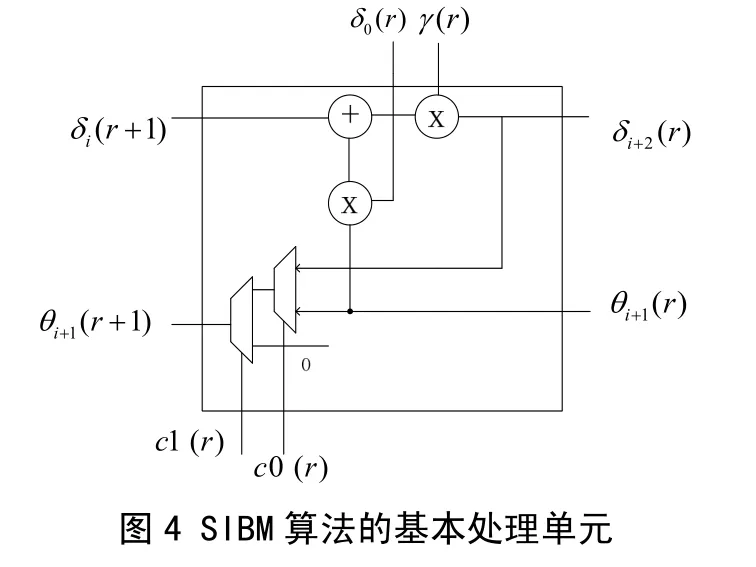
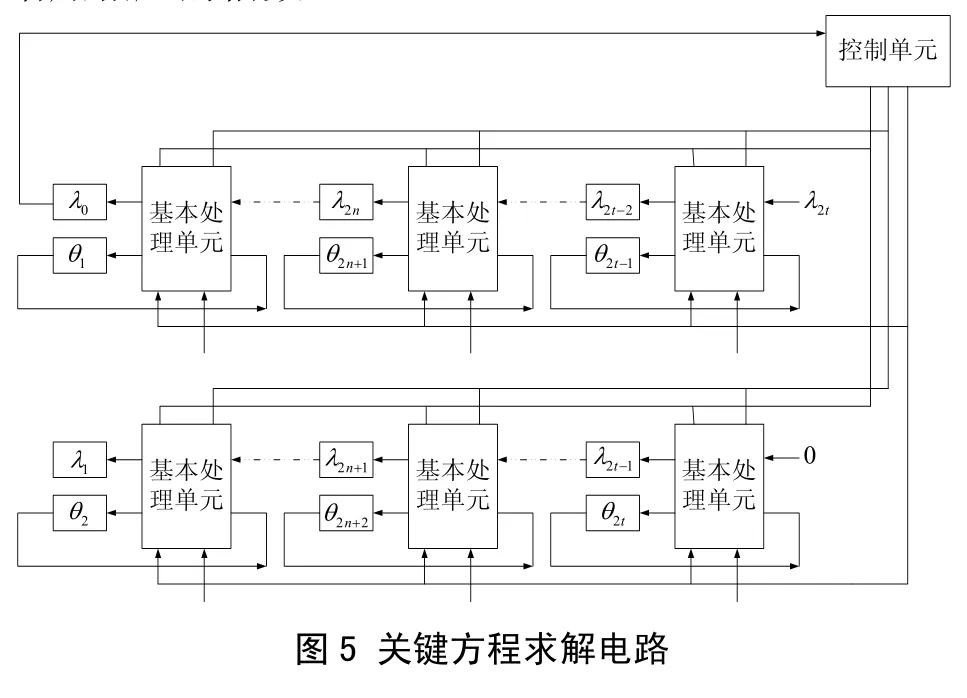
图5是SIBM算法的直接实现。此外，文献[5]还讨论了2-FOLDING和T-FOLDING的实现形式，面积分别减少2、T倍，但会增加译码的延迟时间也会增加相应的倍数。

4 并行钱搜索电路

钱搜索是从高位开始验根，如果λ( αi)==0，表明 i位置为错误位置，需要将该比特求反。由于在闪存控制器中，数据都是Byte为单位存储，是缩短的BCH(n, k)码，验根不是从2M-1开始，而是从n开始，所以要用λ˜i=(α^((2M-1-n) i ))·λi代替λi，代入钱搜索中，如图6所示。对不同的码率n,相应λ˜i/λi=α^((2M-1-n) i )的会不同，为实现多码率，可以根据码率，选择相应的乘法系数，根据乘法系数得到该码率对应的λ˜i，再代入钱搜索电路。

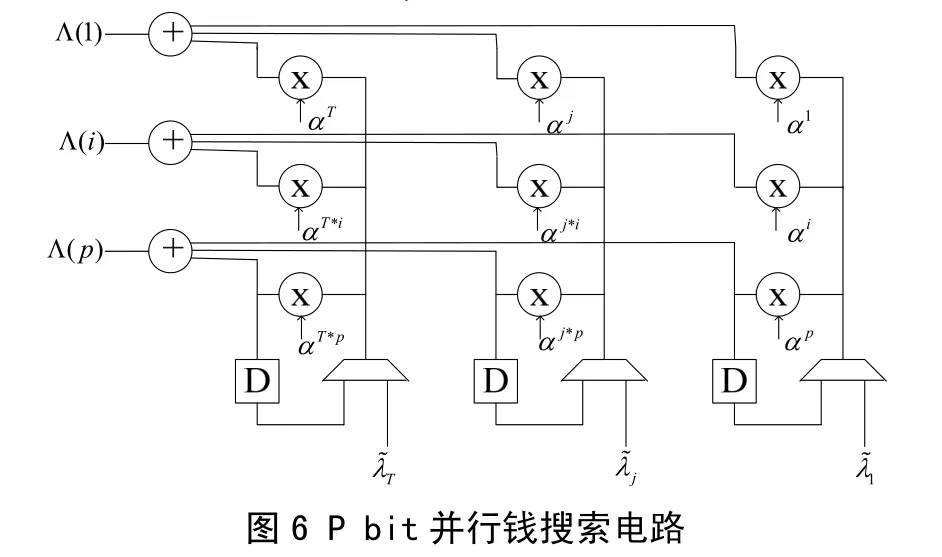
在钱搜索中， 由于乘法器都是固定系数的，可以进行面积优化，文献[8]给出优化的算法，然而，面积的优化将会增加乘法器的延迟，使其从O(lb(M))增加为O(M)。时序分析表明，图6中从λi输入，经过乘法器转化为λi，通过选通器再经过一个乘法器，和另外的32个λi相异或输出，这是个关键路径，可以通过Pipeline的操作，改善时序。

5 仿真综合

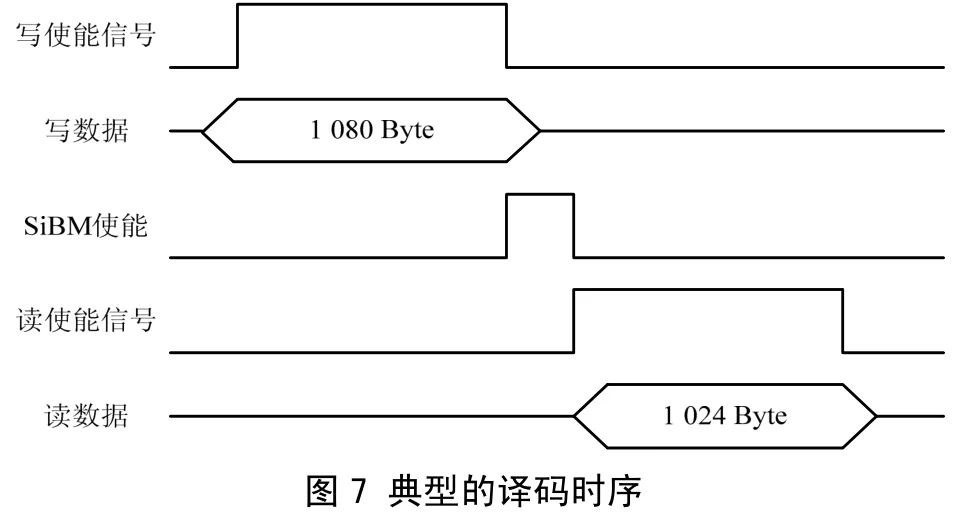
这里是使用System Verilog搭建验证环境，将编解码器对接，并利用约束随机，在信道上产生不多于32 bit的随机错误，生成不同的激励，并判断解码器能否正确的纠正错误。实际仿真证明文中的设计能够每1 024 Byte信息量纠正不超过 32 bit的随机错误。典型的VCS的仿真时序图如图7所示(由于波形太大，只列出示意图)。首先，读取闪存中信息，写入解码器中，共需1 080个时钟周期，信息位使用1 024个时钟周期，冗余校验位使用56个时钟周期；其次利用 SiBM求解关键方程，共需32个时钟周期；最后，从解码器中读取纠正后信息，共需 1 024个周期。此外，BCH解码器可以和 CRC校验级联，用于发现错误多于32 bit的情况。

这里使用TSMC 90 nm工艺库综合，在输入延迟70%、输出 30%的约束下，提出的设计可以工作在200 MHz，面积0.445 mm2，典型的功耗7.8 mW。

6 结语

文中结合实际的项目经验，阐述BCH编解码设计中的设计思想和一些重要的细节。提出的设计相对于其他的设计，主要特点有：首先，提出的设计采用并行的编解码，在相同的系统频率下，可提高译码带宽；其次，在关键方程求解电路中，采用SiBM算法，极大地减小编码器面积；最后，在钱搜索前加入乘法逻辑，可以容易地实现多码率。该BCH编解码器已经成功地应用闪存控制器中，其强大的纠错能力，满足目前市场上主流FLASH的可靠性需求。并在此感谢记忆科技苏州研究院 IC部门同事给予的技术上支持。

[1] 李璐,周海燕. 一种含BCH编解码器的控制器的SLC/MLC NAND FLASH控制器的 VLSI设计[J]. 现代电子技术,2009, 32(07): 167-170.

[2] 王杰,沈海斌. NAND Flash 控制器的 BCH编/译码器设计[J]. 计算机工程, 2010, 16(36): 222-225.

[3] 宁楠,宋文妙. 一种基于FPGA的纠错编码器的设计和实现[J]. 通信技术, 2008, 41(08): 95-97.

[4] 张彦,李署坚，崔金.一种 BCH码编译码器的设计与实现[J].通信技术,2010, 43(12): 24-25.

[5] LIU W, JUNRYE R, SUNG W Y. Low Power High throughput BCH Error Correction VLSI Design for Multi level Cell NAND FI ASH Memorie[C]//IEEE. Signal Processing Systems Design and Implementation.Canada: IEEE Signal Processing Society, 2006:303-308.

[6] SARWATE D V, SHANBHAG N R. High-speed Architectures for Reed-Solomon Decoders[J]. IEEE Trans. on Very Large Scale Integration,2001, 9(05): 641-655.

[7] REYHANI-MASOLEH A, HASAN M A. Low Complexity Bit Parallel Architectures for Polynomial Basis Multiplication over GF(2)[J]. IEEE Trans. on Computers,2004, 53(08): 945-959.

[8] PAAR C. Optimized Arithmetic for Reed-Solomon Encoders[C]//IEEE.1997 IEEE InternationaSymposium on Information Theory.Germany: IEEE,1997:250.