半刚接钢框架－钢板剪力墙结构滞回性能的有限元分析

孙国华，顾 强，何若全，方有珍

（苏州科技学院 江苏省结构工程重点实验室，江苏 苏州215011）

1994年美国Northridge地震、1995年日本阪神地震均暴露出传统梁柱抗弯节点因转动能力不足而产生的脆性裂缝，导致了震后的大规模修复。随后工程界对此展开了大量的研究工作，并提出了一系列解决措施，主要分3个方面：1）对原有传统节点构造进行简单的局部改进，如移除焊接衬板，或对焊接衬板和柱翼缘实施补焊等。2）对梁端局部截面进行削弱处理，确保塑性铰出现在梁的削弱部位，如“狗骨式”节点作法。3）直接加强节点以保证“强节点弱构件”，如在连接处梁翼缘加盖板或梁腋。采用第1种措施改进后的传统节点仍达不到塑性转动能力的要求。“狗骨式”节点、焊接盖板节点、焊接梁腋节点塑性转动能力虽然满足要求，但施工复杂、造价提高［1］。

钢板剪力墙结构（Steel Plate Shear Wall，简称SPSW）由钢框架及钢剪力墙板构成［2－10］，周边的钢框架主要承担竖向荷载和绝大部分倾覆力矩，剪力墙板承担绝大部分水平荷载，提供较大的抗侧刚度，但已有试验研究发现刚接节点仍易发生断裂破坏。将半刚性连接引入至钢板剪力墙结构中，既可避开结构对刚性节点转动能力的要求，避免了节点的脆性断裂，又降低了节点造价，方便施工。为了探讨半刚接钢板剪力墙结构的抗震性能，本文结合文献［11］所做的3层薄钢板剪力墙结构的低周往复加载试验，基于等效拉杆模型［12－15］对半刚接钢板剪力墙结构的滞回性能进行了分析，重点考察了半刚性连接、框架强弱相关因素对钢板剪力墙结构抗震性能的影响。

1 有限元模型的验证与分析

1.1 有限元模型的建立

采用等效拉杆模型模拟钢板剪力墙的滞回性能，钢框架梁、柱采用纤维模型模拟，内填墙拉杆采用只拉不压的纤维模型模拟，恢复力模型见图1。

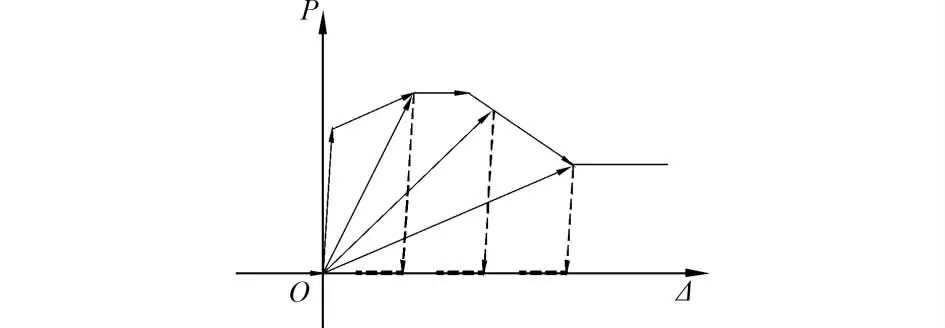
图1 拉杆恢复力模型

选用文献［11］的SPSW－2作为分析的S－BASE试件，试件3层1跨，层高800mm，跨度1 115mm，内填墙板厚度1.1mm。内填钢板fy＝261.7 MPa，fu＝339.9MPa，弹性模量1.91×105MPa；框架柱fy＝278.8MPa，fu＝433.7MPa，弹性模量1.94×105MPa；框架中梁fy＝291.6MPa，fu＝440.5MPa，弹性模量1.96×105MPa；框架顶梁fy＝263.7MPa，fu＝421MPa，弹性模量1.965×105MPa。框架中梁、顶梁、柱截面分别为H150×100×6×9、H300×200×8×12及 H200×200×8×12。双向拉杆有限元模型见图2，其中等效拉杆两端铰接于周边钢框架。

图2 有限元模型

1.2 试验验证

图3给出了S－BASE结构在水平荷载作用下有限元模拟的滞回及骨架曲线同试验结果的对比。其中图3中的试验曲线为文献［11］中SPSW－2的试验结果。

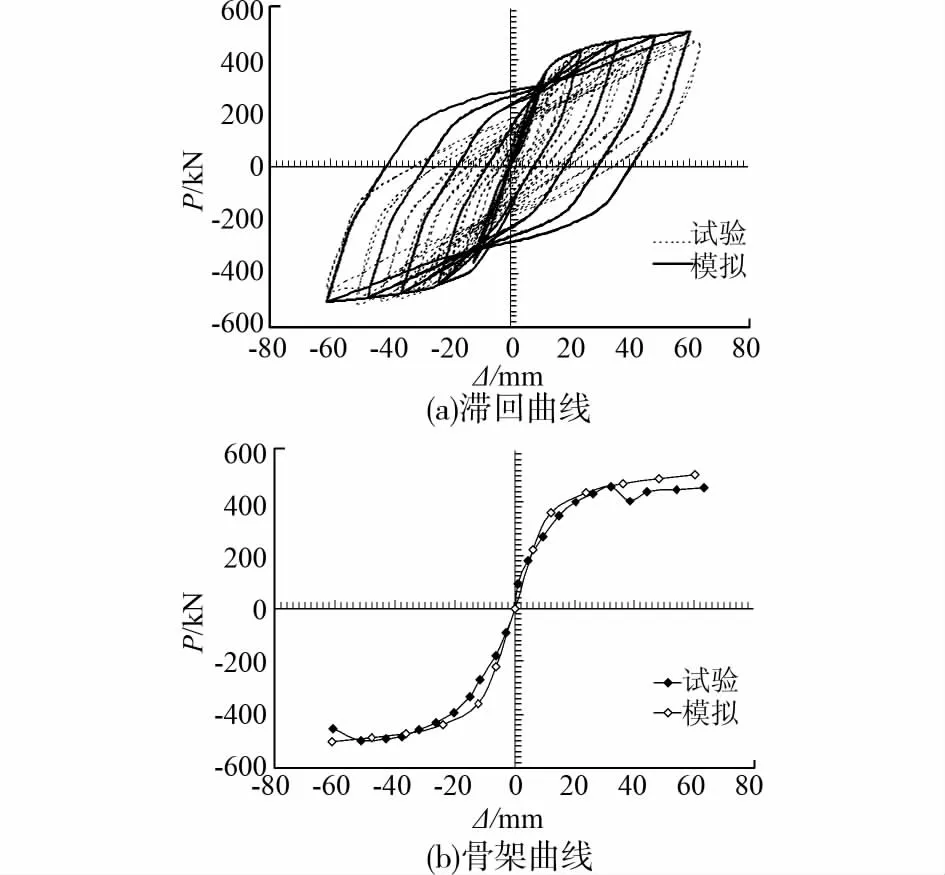
图3 S－BASE试件 P－Δ曲线

由图3可知，模拟的滞回曲线较试验结果略为饱满，模拟曲线中部存在明显的捏缩现象。模拟曲线可以反映加载刚度的衰减，但未能反映卸载刚度的衰减。从整体趋势上模拟的骨架曲线同试验吻合良好，可采用等效双向拉杆模型模拟薄SPSW结构的滞回性能。

1.3 S-BASE试件的滞回性能分析

钢板剪力墙结构由钢框架同内填剪力墙板构成，为了细致地分析S－BASE试件滞回曲线的特点，本文分别给出将梁端、底层柱根部设为铰接的SPSW滞回曲线（用于反映剪力墙板的贡献），以及周边刚接钢框架的滞回曲线（用于反映钢框架的贡献），详见图4。

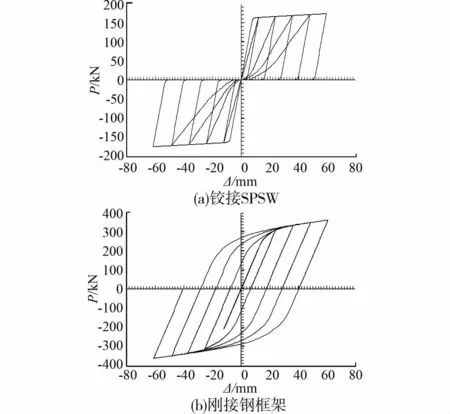
图4 剪力墙板及钢框架P－Δ曲线

由图4可知，钢框架结构的滞回曲线呈饱满的梭形特征，而铰接SPSW结构的滞回曲线呈现严重的捏缩效应。这进一步反映了由钢框架同内填钢板组合而成的SPSW结构滞回曲线具有双重特点，当周边钢框架较强时，滞回曲线由框架滞回特征决定，形状趋于饱满；当内填剪力墙板较强时，滞回曲线由剪力墙板特征决定，形状趋于捏缩。

本文还提取了以S－BASE为基础的刚接SPSW、铰接SPSW、刚接钢框架3种模型的单向骨架曲线，用于定量分析各部分水平剪力的相对比例，来界定SPSW结构钢框架的强弱。

图5给出了3种模型的骨架曲线，图6描述了基于3种模型分析的钢框架及剪力墙板水平剪力的分担比例。

由图5可以看出，在同一顶点位移时刻的铰接SPSW和刚接钢框架结构水平剪力之和大于同时刻的刚接SPSW结构。在顶点位移比2%时刻，超过6.2%。

为了进一步反映钢板剪力墙结构中各部分的贡献，图6给出了两部分所承担的水平剪力与刚接SPSW的比值。由于S－BASE试件周边钢框架设计的相对较强，其水平承载力主要由钢框架提供，内填剪力墙板在初期承担约40%的水平剪力，周边钢框架承担约60%，后期略呈增大趋势。

图5 强框架 钢板剪力墙结构能力曲线

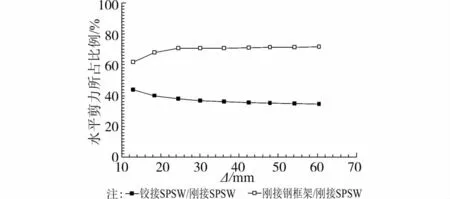
图6 S－BASE试件各部分基底剪力分担比例

下文细致地分析了周边钢框架在强、弱两种情况下，半刚性连接对SPSW结构滞回性能的影响。

2 半刚性连接对强框架SPSW结构滞回性能影响

2.1 强框架SPSW试件设计

以上文分析的S－BASE试件为基础，首先设计5个强框架半刚接SPSW试件。其中，半刚性连接的初始转动刚度按文献［1］所建议的公式（1）确定；节点连接的抗弯承载力分别取相应钢梁塑性抗弯承载力（MPb）的0.00、0.25、0.50、0.75、1.00倍，对应的试件编号分别为 S－SPSW－0.00、S－SPSW－0.25、SSPSW－0.50、S－SPSW－0.75、S－SPSW－1.00。

式中：E为钢材弹性模量；Ib为钢梁的截面惯性矩；Lb为钢梁的几何长度；Ko为梁柱连接的初始转动刚度。

根据本文S－BASE试件的几何参数和实测的力学参数，中部钢梁的初始转动刚度取为2.41×104kN·m／rad，顶部钢梁的初始转动刚度取为2.7×105kN·m／rad；中部钢梁、顶部钢梁实测的塑性抗弯承载力分别为44.6kN·m和222.4kN·m。采用三线性随动强化塑性模型模拟半刚性连接在循环荷载作用下的滞回性能，强屈比（Mu／My）取1.3，并考虑钢材的包辛格效应，恢复力模型见图7。

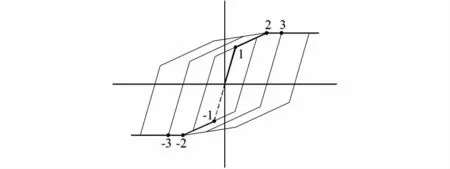
图7 梁柱半刚性连接恢复力模型

2.2 滞回曲线

图8给出了S－SPSW系列试件的滞回曲线。

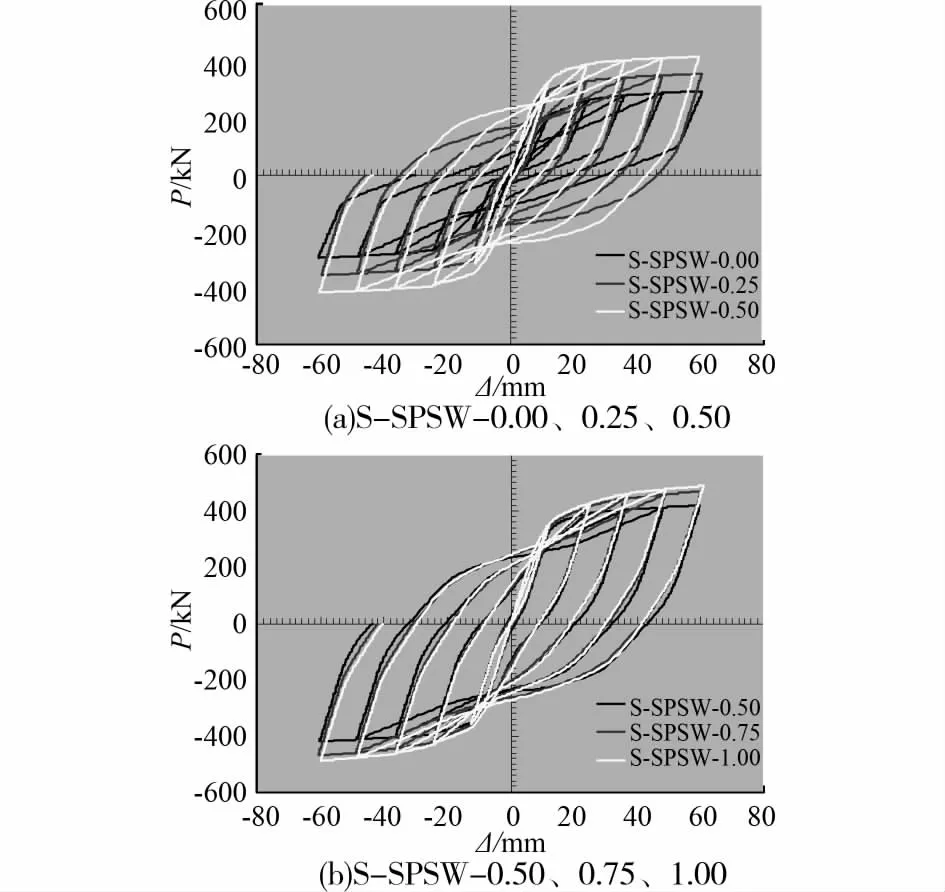
图8 S－SPSW系列试件滞回曲线

由图8可知，随着节点抗弯承载力的增加，SSPSW结构的滞回曲线趋于饱满。这主要因为节点抗弯承载力的增加致使钢框架的承载能力增强，钢框架在SPSW结构中所占比重增加，结构呈现出饱满的滞回特征。特别是当梁柱连接为铰接时，该结构仅反映钢柱与剪力墙板的共同特征，滞回曲线严重捏缩。当节点抗弯承载力等于钢梁抗弯承载力时，强框架SPSW结构滞回曲线饱满，其饱满程度与钢框架同剪力墙板的相对比重相关。

2.3 承载力分析

图9给出了S－SPSW系列试件的骨架曲线。

由图9可知，随着节点抗弯承载力的增加，SSPSW结构水平承载力增大，但增加幅度逐渐减小。在顶点位移比2%时刻，节点抗弯承载力由铰接增至刚接，S－SPSW 水平承载力由288.4kN增至477.1kN，增幅达65.5%。节点的抗弯承载力显著影响S－SPSW结构的水平承载力，主要基于两方面原因。1）节点抗弯承载力直接影响钢框架自身的承载能力；2）节点抗弯承载力的增加，导致钢框架承载力能力的增强，使得钢框架对内填剪力墙板约束能力增强，各板带变形协调一致、充分发挥作用，增加了S－SPSW结构的水平承载力。同时，钢框架是构成S－SPSW结构水平承载力的主要部分，因此节点抗弯承载力是影响强框架SPSW结构水平承载力的主要因素。

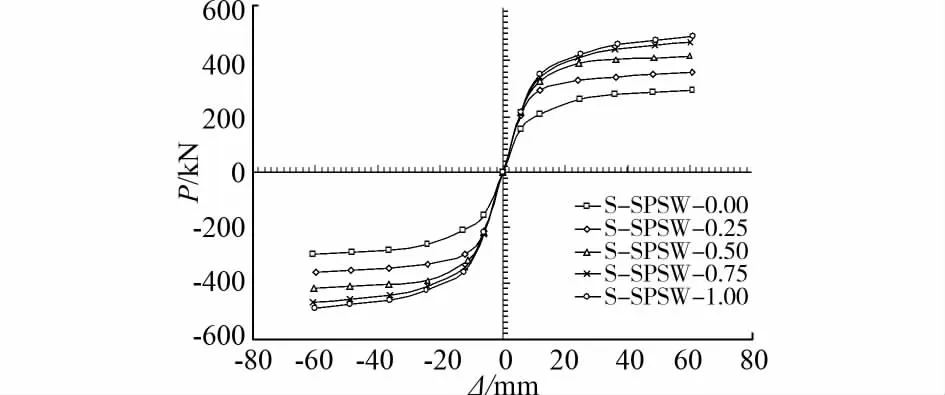
图9 S－SPSW系列试件荷载位移骨架曲线

2.4 抗侧刚度分析

图10 给出了S－SPSW系列试件的抗侧刚度退化曲线。

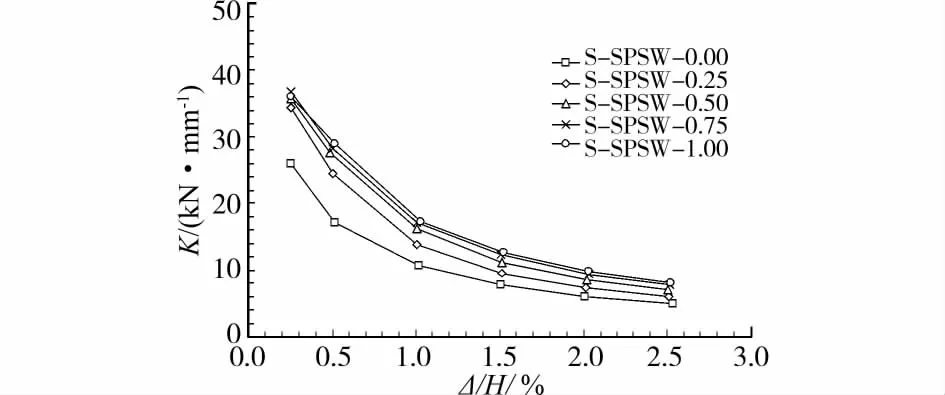
图10 S－SPSW系列试件刚度退化曲线

由图10可知，节点抗弯承载力对S－SPSW结构的抗侧刚度影响较大。节点抗弯承载力越低，钢框架自身的抗侧刚度越低，同时，对内填墙板的约束能力也越低，导致S－SPSW结构的抗侧刚度较低。

2.5 耗能能力影响分析

图11给出了在达到相同顶点位移时刻SSPSW系列试件的滞回耗能。

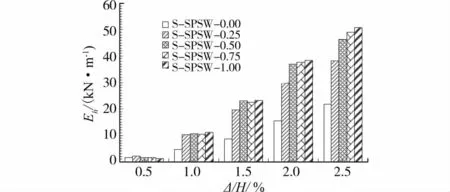
图11 S－SPSW系列试件能量耗散

由图11可知，节点抗弯承载力对SPSW结构的滞回耗能有一定影响。当梁柱连接为铰接时，结构的总体耗能主要由内填钢板提供，耗能能力有限。随着梁柱连接抗弯承载力的增大，钢框架参与耗能比重增大，导致结构整体滞回耗能显著增大。

结构的耗能能力还可以采用等效粘滞阻尼比ζeq来评价，见式（2）。

式中：S（ABC＋ADC）为试件经历一个加载循环所耗散的能量；S（OBE＋ODF）为试件在同级荷载作用下达到最大承载力时所对应的三角形能量，如图12所示。

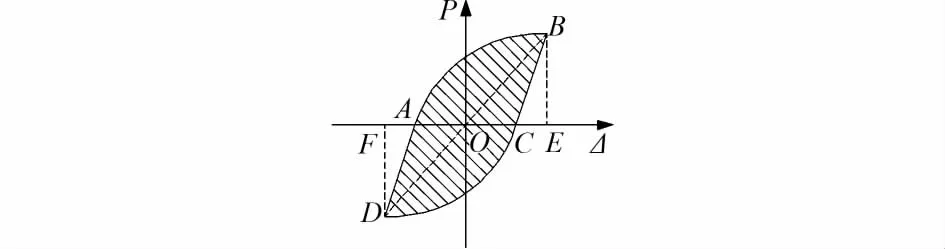
图12 P－Δ滞回曲线

图13 给出了S－SPSW系列试件等效粘滞阻尼比随着水平荷载增加的变化规律。

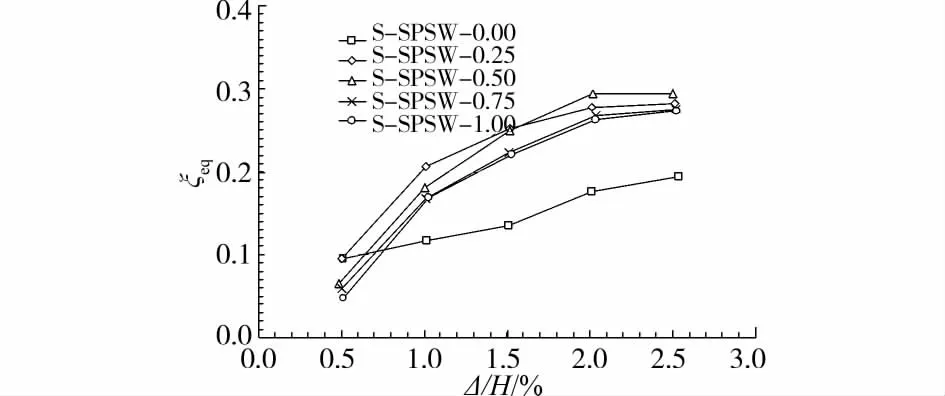
图13 S－SPSW系列试件等效粘滞阻尼比

由图13可知，铰接S－SPSW结构的等效粘滞阻尼比最小，在顶点位移比2%时，为0.18，滞回耗能能力最弱。随着节点抗弯承载力的增大，钢框架参与比重增加，S－SPSW结构的滞回曲线趋于饱满，耗能能力增大，在顶点位移比2%时，最大可达0.29。

3 半刚性连接对弱框架SPSW结构滞回性能影响

3.1 弱框架SPSW试件设计

在BASE试件的基础上，将钢柱截面改为H150×150×6×9，同时将内填钢板厚度调整至1.6mm，设计了弱框架的 W－BASE试件。以 W－BASE试件为基础，通过改变梁柱连接的抗弯承载力，构造了5个弱框架SPSW试件。中部、顶部钢梁的初始转动刚度及梁柱连接的抗弯承载力均与S－SPSW系列试件相同，与节点连接抗弯承载力0.00MPb、0.25MPb、0.50MPb、0.75MPb、1.00MPb倍相对应的试件编号为W－SPSW－0.00、W－SPSW－0.25、W－SPSW－0.50、WSPSW－0.75、W－SPSW－1.00。梁柱连接仍然采用与S－SPSW系列试件相同的恢复力模型。

图14给出了以 W－BASE为基础的刚接SPSW、铰接SPSW、弱刚接钢框架3种模型的骨架曲线。图15描述了基于3种模型分析的弱钢框架及剪力墙板水平剪力的分担比例。

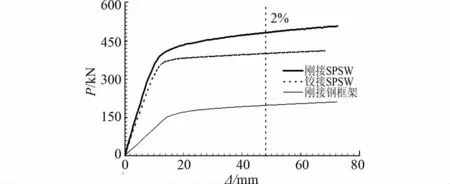
图14 弱框架 钢板剪力墙结构能力曲线

由图14可以看出，在同一顶点位移时刻的铰接SPSW和刚接钢框架结构水平剪力之和大于同时刻的刚接SPSW结构。在顶点位移比2%时刻，刚接SPSW的水平承载力为483.0kN，铰接SPSW为399.8kN，弱刚接钢框架为197.5kN，两者之和超过刚接SPSW结构水平承载力的23.7%。这说明当周边钢框架较为柔弱时，钢框架对内填剪力墙板的协调作用有限，内填剪力墙板未能充分发挥作用。

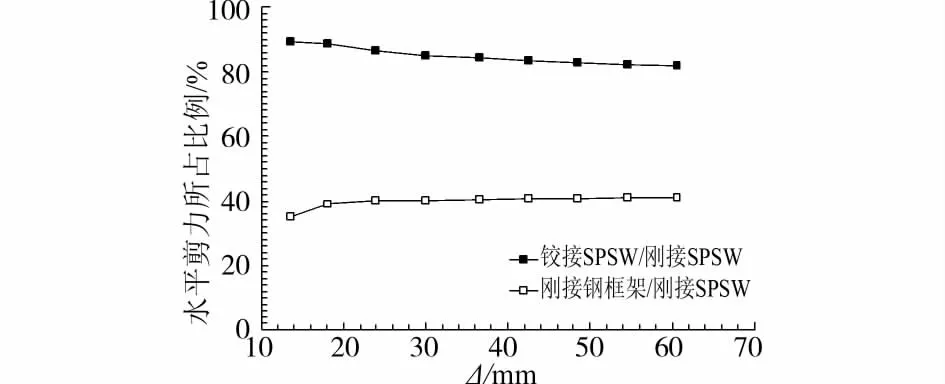
图15 W－BASE试件各部分基底剪力分担比例

图15 定量描述了两部分所承担的水平剪力与刚接SPSW的比值。由于W－BASE试件周边钢框架设计的相对较弱，其水平承载力主要由内填剪力墙板提供，在加载初期内填剪力墙板承担约85%的水平剪力，后期略呈降低趋势。

3.2 滞回曲线

图16给出了W－SPSW系列试件的滞回曲线。

由图16可以看出，当周边弱框架 W－SPSW试件的滞回曲线较强框架S－SPSW试件捏缩严重，加载后期曲线呈明显的反“S”型。这主要由于 WSPSW结构的滞回特征以内填剪力墙板为主。随着节点抗弯承载力的降低，W－SPSW结构的滞回曲线捏缩趋于严重。当周边钢框架过于柔弱时，内填剪力墙板不能充分发挥作用，会导致框架柱提早破坏。

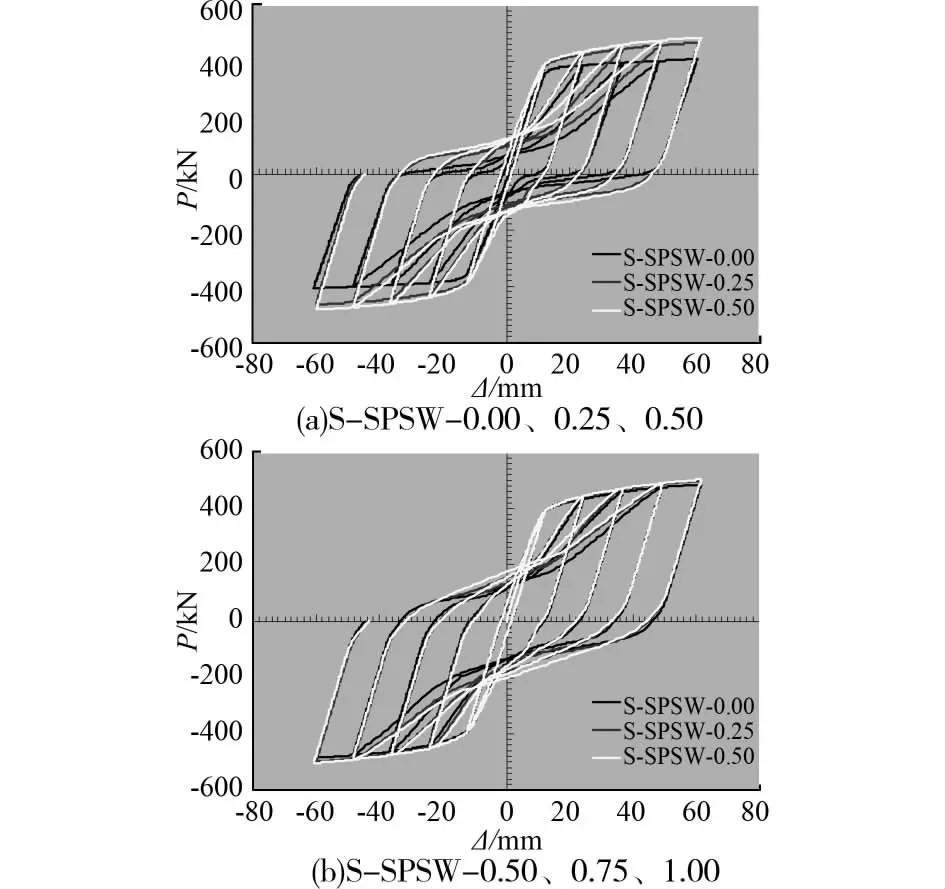
图16 W－SPSW系列试件滞回曲线

3.3 承载力分析

图17 给出了W－SPSW系列试件的骨架曲线。

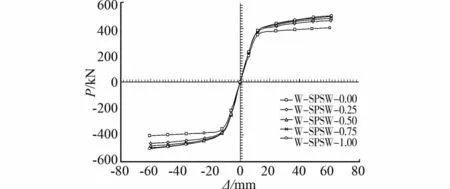
图17 W－SPSW系列试件荷载位移骨架曲线

由图17可知，节点抗弯承载力对弱框架 WSPSW系列试件的最大水平承载力影响程度小于强框架S－SPSW试件。这主要因弱框架对SPSW结构的水平承载力影响较小，而节点抗弯承载力的改变对弱框架承载能力影响程度有限所致。

3.4 抗侧刚度分析

图18给出了W－SPSW系列试件的刚度退化曲线。

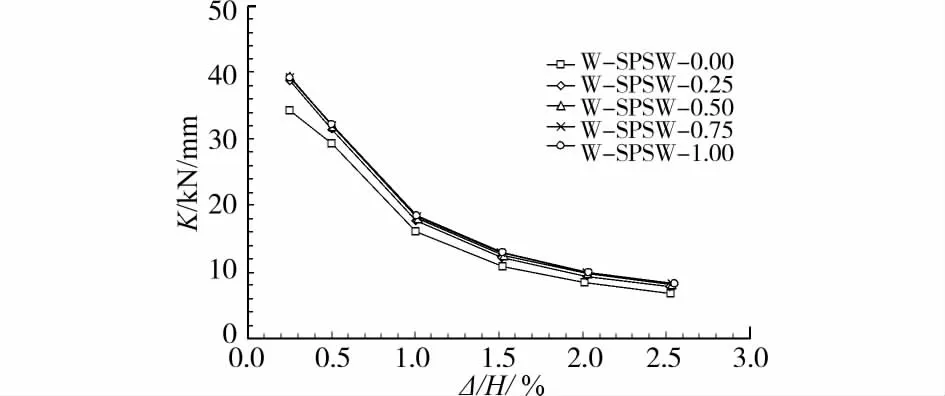
图18 W－SPSW系列试件刚度退化曲线

从图18可以看出，除铰接钢框架 W－SPSW试件的抗侧刚度略小外，节点抗弯承载力对SPSW结构的抗侧刚度影响较小。加载后期，该系列试件的抗侧刚度退化规律和基本一致。

3.5 耗能能力影响分析

图19－20给出了W－SPSW系列试件的能量耗散及等效粘滞阻尼比的对比。

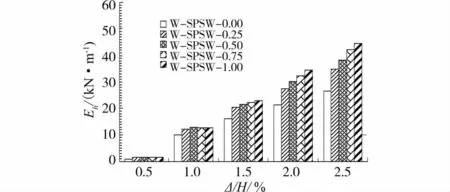
图19 W－SPSW系列试件能量耗散

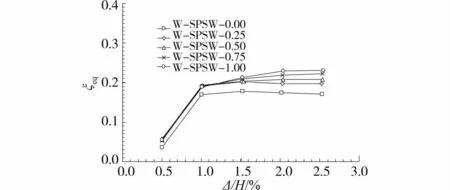
图20 W－SPSW系列试件等效粘滞阻尼比

从图19可以看出，随着节点抗弯承载力的增大，SPSW结构的滞回耗能呈增加趋势。图20表明采用弱框架导致SPSW结构滞回耗能能力降低，其中铰接SPSW结构仍然反映的是内填剪力墙板的耗能能力，因此，节点抗弯承载力及周边钢框架对其影响不大，在顶点位移比2%时为0.17，同铰接强框架SPSW试件的等效粘滞阻尼比基本相同。其它试件的等效粘滞阻尼比在顶点位移比2%时刻，大约为0.2，小于周边强框架的SPSW结构的耗能能力。

4 结 论

本文基于等效拉杆模型对文献［11］中SPSW－2试验试件进行了模拟，在验证了模拟结果合理、可靠的基础上，系统分析了半刚性连接、框架的强弱对钢板剪力墙结构滞回性能的影响。

1）钢板剪力墙结构的滞回性能具有双重特征，当周边钢框架较强时，其滞回曲线较为饱满，滞回特征趋于钢框架结构；当周边钢框架较弱时，其滞回曲线较为捏缩，滞回特征趋于内填剪力墙板。

2）梁柱连接的抗弯承载力对SPSW结构的滞回特征有显著影响，无论周边采用强框架的SPSW结构还是弱框架的SPSW结构，均随着节点抗弯承载力的增加，滞回曲线趋于饱满，耗能能力增强。

3）随着节点抗弯承载力的增加，钢框架自身的承载能力增大，同时对内填剪力墙板的约束效应增强，SPSW结构的水平承载力呈增大趋势；但对强框架SPSW结构影响程度较大，而对弱框架SPSW结构的影响程度相对较小。

4）节点抗弯承载力对强框架SPSW结构的抗侧刚度影响较大，而对弱框架SPSW结构的抗侧刚度影响相对较小。

［1］孙国华.半刚接钢框架内填RC墙结构滞回性能研究［D］.北京：北京工业大学，2010.

［2］Berman J，Bruneau M.Experimental investigation of light－gauge steel plate shear walls.ASCE Journal of Structural Engineering，2005，131（2）：259－267.

［3］Chen S J，Chyuan J.Cyclic behavior of low yield point steel shear wall［J］.Thin－walled Structures，2006，44：730－738.

［4］Hong G P，Jae H K，Sang W J，et el.Framed steel plate wall behavior under cyclic lateral loading ［J］.ASCE Journal of Structural Engineering，2007，133（3）：378－388.

［5］Bing Q，Michel B，Chih H L，et al.Testing of Full－Scale Two－Story Steel Plate Shear Wall withReduced Beam Section Connections and Composite Floors［J］.ASCE Journal of Structural Engineering，2008，134（3）：364－373.

［6］Mehdi H K， Kharrazia， Helmut G L，et al.Implementation of M－PFI method in design of steel plate walls ［J］.Journal of Constructional Steel Research，2008，64：465－479.

［7］Alinia M M，Habashi H R，Khorram A.Nonlinearity in the postbuckling behaviour of thin steel shear panels［J］.Thin－walled Structures，2009，47：412－420.

［8］Anjan K B，Robert G，et al.Seismic analysis of steel plate shear walls considering strain rate and P－delta effects［J］.Journal of Constructional Steel Research，2009，65：1149－1159.

［9］陈国栋，郭彦林，范珍，等.钢板剪力墙低周反复荷载试验研究［J］.建筑结构学报，2004，25（1）：71－78.CHEN Guodong，GUO Yanlin，FAN Zhen，et al.Cyclic test of steel plate shear wall［J］.Journal of Building Structures，2004，25（1）：71－7.

［10］蔡克铨，林盈成，林志翰.钢板剪力墙抗震行为与设计［J］.建筑钢结构进展，2007，9（5）：19－25.CAI Kequan LIN Yingcheng，LIN zhihan.Seismic responses and design of steel plate shear wall［J］.Progress in Steel Building Structures，2007，9（5）：19－25.

［11］邵建华.抗弯钢框架－钢板剪力墙的结构影响系数与位移放大系数研究［D］.南京：河海大学，2008.

［12］Driver R G，Kulak G L，Elwi A E，et al.FE and simplified models of steel plate shear wall［J］.ASCE Journal of structural engineering，1998，124（2）：121－130.

［13］Berman J，Bruneau M.Plastic analysis and design of steel plate shear wall［J］.ASCE Journal of structural engineering，2003，129（11）：1448－1456.

［14］邵建华，顾强，申永康.多层多跨钢板剪力墙水平极限承载力分析［J］.重庆建筑大学学报，2008，30（2）：71－74.SHAO Jianhua， GU Qiang， SHEN Yongkang.Horizontal ultimate bearing capacity analysis of multistory multi－span steel plate shear walls system ［J］.Journal of Chongqing Jianzhu University，2008，30（2）：71－74.

［15］曹春华，郝际平，王迎春，等.钢板剪力墙简化模型研究［J］.建筑钢结构进展，2009，11（1）：28－32.CAO Chunhua，HAO Jiping，WANG Yingchun，et al.Study of steel plate shear walls using the simplified model［J］.Progress in Steel Building Structures，2009，11（1）：28－32.