混凝土空心砌块砌体抗震抗剪强度

吕伟荣，施楚贤，刘锡军，胡张齐

（1.清华大学 土木工程系，北京100084；2.湖南科技大学 土木工程学院，湖南 湘潭411201；3.湖南大学 土木工程学院，长沙410082）

随着竖向压应力σy的增加，混凝土空心砌块砌体的剪切破坏依次表现为剪摩、剪压和斜压3类破坏形态［1－5］，如图1所示，而与之对应的分别是库仑、主拉应力和主压应力理论［1，6－12］，如图2所示。但是，中国现行《砌体结构设计规范》［13］（简称砌体规范）和《建筑抗震设计规范》［14］（简称抗震规范）对混凝土空心砌块砌体的静力和抗震抗剪强度采用了各自不同形式的库仑理论公式，两者不仅在计算方法上不统一，而且在可靠度的取值上也与相对成熟的烧结普通砖砌体相差较大。具体表现在以下几个方面：

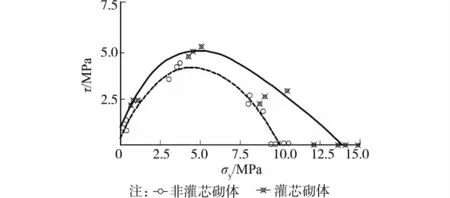
图1 混凝土砌块砌体剪压相关试验曲线［2］

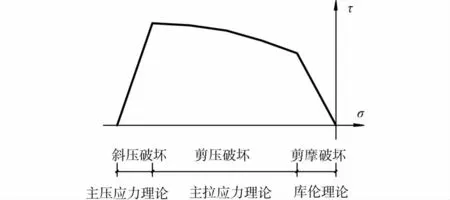
图2 砌体的剪压相关理论［3］

1）正如图1、2所示，单一的库伦理论公式仅适用于其对应的剪摩破坏，而对于另两类破坏形态，特别是具有明显下降段的斜压破坏，则拟合较差，甚至偏于不安全［1］。

2）如图3所示，尽管现行抗震规范较2001版规范在混凝土空心砌块砌体的抗震抗剪强度计算上进行了调整，但当σ0／fv大于16时，按水平段取值仍不具备下降段，与实际明显不符，不能满足日益增长的高层配筋砌体结构设计［15－16］的要求。

3）以 MU10、M7.5的烧结普通砖砌体和MU10、Mb7.5的混凝土砌块砌体为例（取永久荷载分项系数γG＝1.2），如图3所示，对于国内试验数据相对较多，运用也较为成熟的烧结普通砖砌体，其静力抗剪强度曲线①普遍高于抗震抗剪强度曲线③；而对实验数据相对较少的混凝土空心砌块砌体，其静力抗剪强度曲线②普遍低于抗震抗剪强度曲线④。两本规范对于这两类砌体结构在抗剪强度计算上表现出来的不同规律，值得商榷。

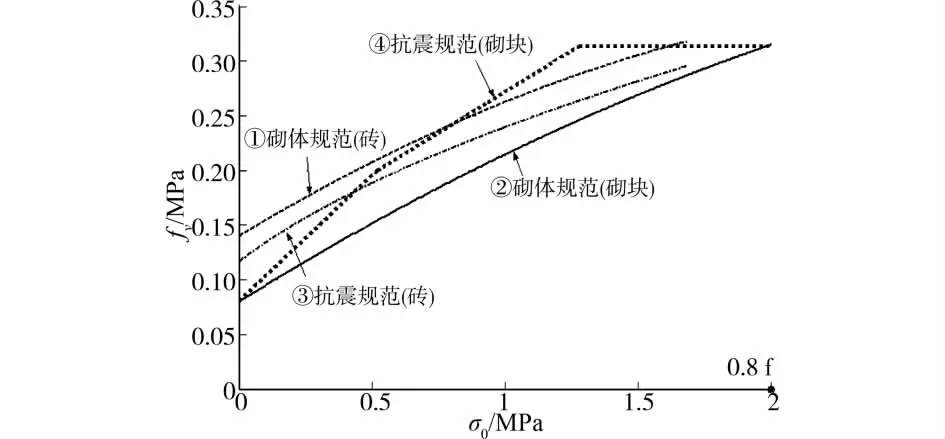
图3 现行砌体规范和抗震规范中砌体的抗剪强度比较

综上所述，现行抗震规范采用库伦理论公式计算混凝土空心砌块砌体的抗震抗剪强度不仅不全面，而且其可靠度也值得质疑。针对以上问题，李晓文［17］、骆万康［18］、蔡勇［8，12］、梁建国［19］等中国学者均对此进行了系统地研究，并提出了各自的计算公式，但均无法实现对剪摩、剪压和斜压三类破坏形态的全面模拟。

为此，本文作者于2008年提出了砌体剪压破坏区理。该理论认为，既然在多数的砌体剪压试验中剪摩与剪压破坏或剪压与斜压破坏共同出现，不妨将砌体的三类剪压复合破坏分为剪摩 剪压破坏区和剪压 斜压破坏区，通过引入权函数，推导出相应的砌体静力与动力抗剪强度简化公式［11］：

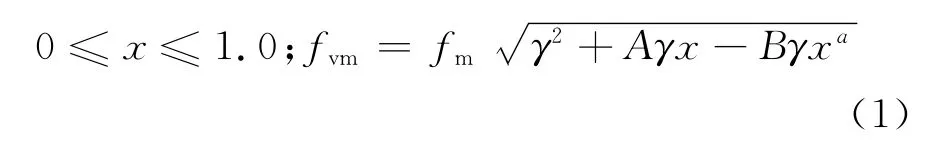
其中A、B及a需根据试验结果确定。在文［11］中，尽管也曾提出了混凝土空心砌块砌体的抗震抗剪强度公式，但该公式中A、B及a等参数的确定仅仅是在其静力抗剪强度公式的基础上，简单的对其曲线峰值折减15%得到，缺乏试验支持。

因此，本文将基于砌体剪压破坏区理论，引入近年来收集到的中国58片混凝土砌块砌体墙的剪压试验结果［19］，在保证可靠度的基础上，运用曲线拟合方法，确定式（1）的3个参数，提出了剪压复合作用下混凝土砌块砌体抗震抗剪强度设计值全曲线公式，解决了现行砌体和抗震规范中存在不合理和不安全的问题。

1 剪压复合作用下混凝土空心砌块砌体的抗剪强度全曲线

砌体剪压破坏区理论简化公式（1）具有下降段，能较全面的模拟砌体剪压破坏全曲线。为此，本文根据图1曲线中相关数学特征，可对公式（1）中的参数A、B及a确定如下：

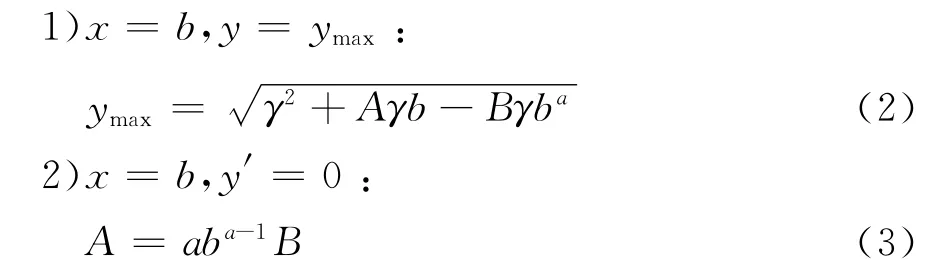
根据中国现有的58片不同高宽比、不同试件尺寸、不同加载方式的混凝土空心砌块砌体结构试验结果［19］，如图4所示，同时参考相关文献研究成果，对剪压复合作用下混凝土空心砌块砌体抗剪强度曲线的关键参数取值如下：

1）曲线峰值点坐标（b，ymax）的取值

如图5所示，对于坐标系统为x＝σy／fm、y＝fvm／fm的混凝土空心砌块砌体的剪压相关曲线而言，相关文献中横坐标b的取值各不相同：重庆建筑大学骆万康教授（1999年）对于普通粘土砖动力剪切试验回归曲线峰值点取为0.502；湖南大学刘桂秋教授（2000年）对于砌体结构统一取为0.67［10］；而对于混凝土而言，其剪压相关曲线峰值坐标为0.60。综合以上取值，并考虑到动力试验的取值相对偏低，本文建议取为0.55。

而对于曲线峰值纵坐标ymax，则根据文［19］试验回归结果确定为0.20。

2）参数γ＝fv0，m／fm的取值

在每次混凝土砌块砌体抗剪试验中，γ值均不相同，存在较大的变异性，本文从试验结果推导如下：

a）由文［19］的试验数据分布情况（详见图4）可知，峰值数据点的最大横坐标可近似取为8，即：σy，m／fv0，m＝8；

b）对于坐标系统为x＝σy／fm、y＝fvm／fm的混凝土空心砌块砌体的剪压相关曲线而言，其峰值横坐标b＝0.55，应与图4峰值点相对应，经坐标换算后可推导出：γ＝fv0，m／fm＝b／8＝0.07。

将曲线峰值点坐标（0.55，0.20）及γ＝0.07代入（2）～（4）式，可求解得：a＝2.81，A＝1.40，B＝1.47，代入式（1）即可得到剪压复合作用下混凝土空心砌块砌体的抗震抗剪强度平均值公式：

如图4所示，文［19］的试验值与式（6）计算值比值的平均值为1.27，变异系数为0.245，两者吻合较好，且式（6）的计算值偏于安全。

同时，与文［19］的公式相比，式（6）的改进在于：1）具有下降段，能全面的反映剪压复合作用下混凝土空心砌块砌体的剪摩、剪压及斜压3个破坏阶段；2）解决了文［19］的计算取值偏于保守的取值，即当σy，m／fv0，m＞5，文［19］取值为水平直线。同时，当σy，m／fv0，m＞13.1，文［19］的计算取值由于缺乏下降段而导致不安全，无法适用于高层配筋砌块砌体结构。

图4 剪压复合作用下混凝土空心砌块砌体抗剪强度

2 混凝土空心砌块砌体抗震抗剪强度设计值公式

2.1 γ的取值

与试验平均值公式取值不同，现行砌体规范中已明确给出了fv0和f的取值，根据砌体规范表3.2.2所列的混凝土砌块砌体类型，可计算出γ的范围在（0.015～0.050）之间，平均值为0.026，如表1所示，故近似取γ＝0.03。

表1 规范中不同组合下混凝土空心砌块砌体γ的计算值

2.2 抗震抗剪强度设计公式的确定

根据可靠度理论，砌体的强度设计设计值f与强度平均值fm的关系为：

式中，γf为砌体结构的材料性能分项系数，一般情况下，宜按施工控制等级为B级考虑，取1.6［13］；σf为砌体强度的变异系数，计算抗剪强度时一般取0.2［1］。

将γf＝1.6，σf＝0.2代入式（7），可得：f＝0.42fm。考虑到设计公式也应满足剪压复合条件下混凝土空心砌块砌体结构的破坏特点，即满足式（2）～（4），故处理如下：

1）曲线起点下调，即fv0根据砌体规范表3.2.2所规定近似取值，即fv0＝0.03f。

2）曲线峰值点根据式（5）的计算结果取f＝0.42fm，即ymax＝0.20×0.42，b值仍为0.55。

3）同求解（2）～（4）的过程，解方程确定相关参数。

由上述条件求解得：a＝2.92；A＝0.38，B＝0.41，代入式（1）即可得到剪压复合作用下混凝土砌块砌体的抗震抗剪强度设计公式：

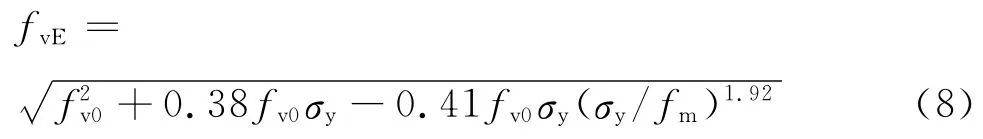
如图5所示，本文提出的混凝土空心砌块砌体抗震抗剪强度设计公式（8）与试验平均值公式（5）相比，不仅具有可靠度保障，而且具有与试验曲线及理论分析相同的特征。为方便工程应用，本文对表1中的各种混凝土砌块砌体组合按式（8）的计算结果与现行规范中所采取的公式计算结果进行了对比，部分结果如下图6所示。

图5 混凝土空心砌块砌体抗剪强度公式比较

图6 现行砌体规范中各种类型的混凝土砌块砌体抗剪强度曲线对比

图6的计算结果表明：1）本文提出的混凝土空心砌块砌体抗震抗剪强度公式（8）普遍低于现行规范规定的混凝土砌块砌体静力抗剪强度计算值，不仅提高了其抗震可靠度，而且较好的统一、协调了烧结普通砖砌体和混凝土砌块砌体的抗震与静力抗剪强度设计值之间的变化关系。2）不同类型的混凝土砌块砌体按式（8）计算的抗震抗剪强度均在σy＝f时趋于0，较好地实现了对砌体剪压相关曲线中3个破坏形态的模拟，避免了现行规范中抗剪强度单调递增的不合理和不安全。

3 结论

1）在砌体剪压复合破坏区理论基础上，根据中国已有的58片灌芯砌块砌体墙片试验结果，推导出混凝土砌块砌体的剪压相关性试验值曲线公式（5）。与传统砌块砌体剪压相关曲线相比，该曲线不仅光滑连续，而且具有下降段。

2）通过对式（5）曲线顶点按f＝0.42fm进行折减以及起点、终点的相关处理后，本文推导出具有一定可靠度保证的混凝土空心砌块砌体抗震抗剪强度设计值公式（8）。如图5所示，经式（8）的计算得到的凝土空心砌块砌体抗震抗剪强度设计值不仅低于现行抗震规定的抗震抗剪强度，而且也普遍低于现行规范砌体规定的静力抗剪强度，这表明式（8）不仅满足设计可靠度要求，而且较好的统一、协调了烧结普通砖砌体和混凝土砌块砌体的抗震与静力抗剪强度设计值之间的变化关系。

3）如图6所示，本文提出的混凝土空心砌块砌体抗震抗剪强度设计公式（8）不仅具有下降段，且对于不同类型的砌块砌体组合基本上均在主压应力σy＝f时趋于0，较好地实现了对砌体剪压相关曲线中各种破坏形态的模拟，能直接运用于高层砌体结构设计，避免了现行规范中抗剪强度单调递增的不合理和不安全。

［1］施楚贤.砌体结构理论与设计：2版［M］.北京：中国建筑工业出版社，2003.

［2］Ahmad A，Hamid and Robert G，Drysdale.Concrete masonry under combined shear and compression along the mortar joint［J］.ACI Journal，1980，77（5）：314－320.

［3］Riddington J R，Ghazali M Z.Hypothesis for shear failure in masonry joints［C］.Proc.Instn Civ.Engrs，part2，1990（3）：89－102.

［4］Graubner C A，Kranzler T.Shear design of unreinforced masonry panels ［C］.In：10th Canadian Masonry Symposium.Banff，Alberta，2005，on CD－ROM.

［5］Shieh－Beygi B，Pietruszczak S.Numerical Analysis of Structural Masonry：Mesoscale Approach［J］.Computers and Structures，2008，86：1958－1973.

［6］Andreaus U.Failure criteria for masonry panels under in－plane loading［J］.Journal of Structure Engineering，1996（122）：37－46.

［7］Mann W，Mǖller H.Failure of shear－stressed masonryan enlarged theory，tests and application to shear walls［C］／／Proc.，British Ceramic Soc.，1982（30）：223－235.

［8］蔡勇，施楚贤，马超林，等.砌体在剪－压作用下抗剪强度研究［J］.建筑结构学报，2004，25（5）：118－123.CAI Yong，SHI Chuxian，MA Chaolin，et al.Study of the masonry shear strength under shear－compression action［J］.Journal of Building Structures，2004，25（5）：118－123.

［9］洪峰，王绍博.砌体结构抗震抗剪强度分析［J］.地震工程与工程振动，2000，20（3）：28－33.HONG Feng，WANG Shaobo.Analysis of earthquake shear strength of masonry structures［J］.Earthquake Engineering and Engineering Vibration，2000，20（3）：28－33.

［10］刘桂秋，施楚贤.平面受力砌体的破坏准则［C］／／2000年全国砌体建筑结构学术交流会议论文集.北京：中国建筑工业出版社，2000：19－24.

［11］吕伟荣，施楚贤，刘桂秋.剪压复合作用下砌体的静力与抗震抗剪强度［J］.工程力学，2008，25（4）：158－164.LU Weirong，SHI Chuxian，LIU Guiqiu.Static and seismic shear strength of masonry under shear－compression loading［J］.Engineering Mechanics，2008，25（4）：158－164.

［12］蔡勇.砌体在剪 压复合作用下抗震抗剪强度分析［J］.建筑结构，2011，41（2）：74－77.CAI Yong.Analysis on aseismic shear strength of masonry under shear－compression composite action［J］.Building Structure，2011，41（2）：74－77.

［13］中华人民共和国建设部.GB 50003－2001砌体结构设计规范［S］.北京：中国建筑工业出版社，2001.

［14］中华人民共和国建设部.GB 50011－2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.

［15］金伟良，岳增国，高连玉.《砌体结构设计规范》的回顾与进展［J］.建筑结构学报，2010，31（6）：22－28.JIN Weiliang，YUE Zengguo，GAO Lianyu.State－ofthe－art development on ‘Code for design of masonry structures’［J］.Journal of Building Structures，2010，31（6）：22－28.

［16］施楚贤.对砌体结构类型的分析与抗震设计建议［J］.建筑结构，2010，40（1）：74－76.SHI Chuxian.Analysis for dividing types of masonry structures and seismic design recommendations ［J］.Building Structure，2010，40（1）：74－76.

［17］李晓文，王庆霖.无筋墙体抗剪计算［C］／／2000年全国砌体建筑结构学术交流会议论文集.北京：中国建筑工业出版社，2000：59－65.

［18］骆万康，李锡军.砖砌体剪压复合受力动、静力特性与抗剪强度公式［J］.重庆建筑大学学报，2000，22（4）：13－19.LUO Wankang，LI Xijun.A study on the response of brick masonry structure under dynamic and static shearcompression loading and suggested shearing equation［J］.Journal of Chongqing Jianzhu University，2000，22（4）：13－19.

［19］梁建国，方亮.混凝土空心砌块砌体抗震抗剪强度研究［J］.建筑结构，2009，39（1）：45－47.LIANG Jianguo，FANG Liang.Seismic shear strength of concrete hollow block masonry ［J］.Building Structure，2009，39（1）：45－47.