土水特征曲线参数的概率统计及敏感性分析

谭晓慧，李 丹，沈梦芬，侯晓亮，胡 娜

（合肥工业大学 资源与环境工程学院，合肥230009）

土水特征曲线（Soil－water characteristic curve，简称SWCC）表征非饱和土的基质吸力与含水率（如重力含水率、体积含水率）或饱和度之间关系，它包含了土体在任一吸力时孔隙中含有的水量及孔径分布信息，由土水特征曲线可以得到非饱和土的抗剪强度、渗透系数、体积变化等性质［1－5］。由于土水特征曲线的重要性，很多学者对之进行了研究，并提出了大量有关土水特征曲线的数学模型［6－7］。文［1，6－7］通过研究，指出 Frenlund－Xing模型（简称 FX模型）［10］及van Genutchen模型（简称 VG 模型）［11］效果较好，它们适用的吸力范围广，拟合参数的物理意义明确。采用数学模型来表示SWCC的优点在于：模型的参数可以量化描述曲线的形状，可用于土体的分类，可方便地用于估计其它土性参数。在涉及到非饱和土的岩土工程数值分析中，非饱和土的性质非常重要，数值分析的结果是否正确在很大程度上依赖于SWCC参数等输入数据的可靠性。在进行可靠度分析时，还需要提供参数的均值、均方差、分布类型等信息。因此，对SWCC模型参数进行概率统计分析是十分重要的。

Sillers等［7］通过对二百多组数据的数理统计，对8种土的多种SWCC模型及其修正型式求得了模型参数的均值、均方差及中值，并指出在大多数情况下，这些拟合参数的变异性都较大。Puppala等［8］采用FX模型研究了2种膨胀土的SWCC特征，并采用线性回归分析的方法求解了模型参数与基本土性参数间的关系。Phoon等［9］以VG模型为基础，指出可采用对数正态随机矢量来表示SWCC的2个拟合参数a及n。

由于FX模型及VG模型的拟合效果较好［1，6－7］，笔者以这2类模型及其修正型式为基础，研究SWCC参数的拟合方法，分析不同土类的SWCC参数的概率分布特征，并进行参数的敏感性分析。

1 土水特征曲线模型及拟合方法

1.1 SWCC模型

SWCC可以通过某种数学模型来表示，即：采用某种特定型式的函数来表示试验所得的基质吸力与含水率的关系。笔者以FX模型和VG模型为基础进行研究。根据具体表达式的不同，这2类模型又分别分为3种型式，具体如下。

1.1.1 FX模型 文［10］通过对土体孔径分布曲线的研究，用统计分析理论推导出非饱和土体积含水率与基质吸力之间的对数函数型式的土水特征曲线，其归一化表达式如下（FX1模型）：

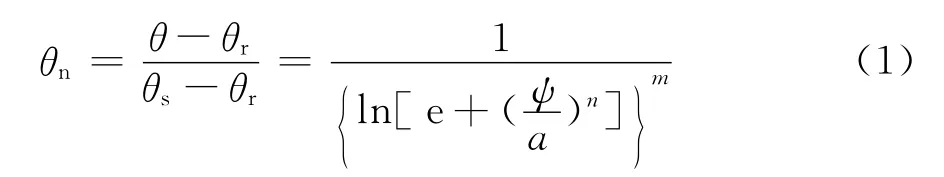
式中：ψ为基质吸力；θ为与基质吸力ψ相对应的体积含水率，其取值范围为［θr，θs］，θr和θs分别为残余含水率和饱和含水率；θn为归一化的体积含水率（有效饱和度）；a、n、m为拟合参数（a是与进气值有关的吸力值，对应于曲线的拐点；n是与孔径分布有关的参数，对应于曲线的斜率；m是与曲线拐点处的不对称性有关的参数）；e为自然对数的底。

若在曲线拟合时视残余含水率为零，则上式变为（FX2模型）：

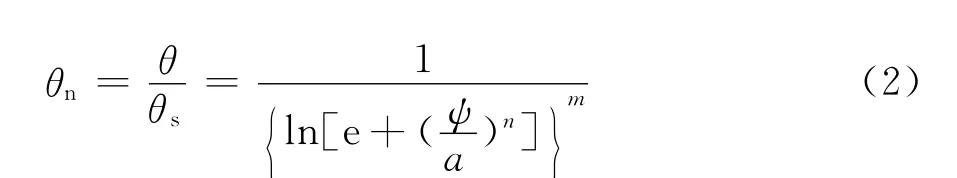
当土体的体积含水率小于残余含水率时，上述模型常高估了含水率的数值。此时，可采用下述方法进行修正（FX3模型）：

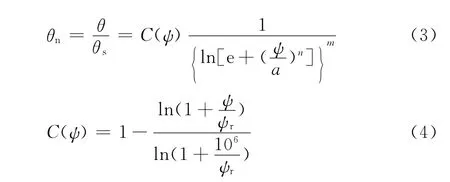
式中：C（ψ）为修正函数，ψr为与残余含水率θr对应的基质吸力，一般取ψr＝3 000kPa［7］。

1.1.2 VG模型 文［11］通过对土水特征曲线的研究，得出非饱和土体积含水率与基质吸力之间的幂函数形式的土水特征曲线，其归一化表达式如下（VG1模型）：

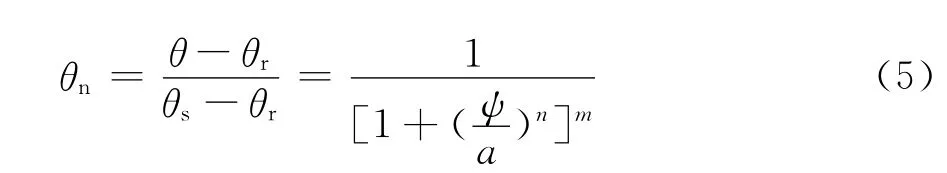
与Fredlund－Xing模型类似，van Genutchen模型亦可写成如下2种型式［7］：

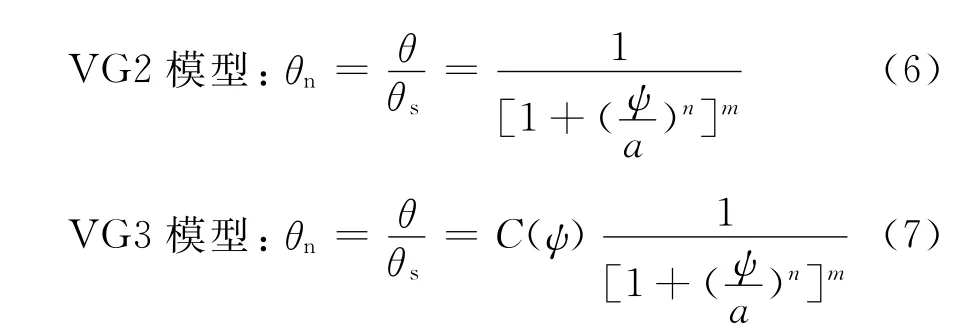
1.2 SWCC拟合方法

对于任一组基质吸力－体积含水率试验数据，为获得上述各种SWCC模型的拟合参数，笔者分别采用科学编程语言MATLAB中的非线性回归拟合函数Nlinfit、最小二乘法拟合函数Lsqcurvefit及最优化求最小值函数Fminsearch来进行SWCC参数的求解。

方法1：Nlinfit是Matlab统计工具箱中的非线性回归函数，它采用Levenberg－Marquardt算法来进行非线性回归。它需要的输入值是：待拟合的数据、非线性曲线函数及拟合参数的初值。

方法2：Lsqcurvefit是Matlab优化工具箱中的函数，它采用最小二乘法来求解非线性函数的参数。它需要的输入值除了待拟合的数据、非线性曲线函数及拟合参数的初值以外，还可以限定所需求解参数的范围。

方法3：Fminsearch属于 Matlab的基本函数，它采用不需求导数的优化方法来求解无约束多变量函数的最小值。它需要的输入变量是目标函数及参数的初值。笔者定义目标函数值为体积含水率的拟合值与实测值之差的平方和。因此，用这种方法求解参数的实质也是最小二乘法。

2 土水特征曲线的拟合

为了研究各种不同土的SWCC形状及特性，分析SWCC模型、拟合方法等因素对参数拟合结果的影响，对大量的基质吸力－体积含水率数据进行了参数拟合及统计分析。

2.1 数据来源

2.1.1 UNSODA数据库中的黏土和砂土

UNSODA是由美国农业部盐度实验室开发的有关非饱和土性质的数据库，全称为非饱和土水力数据库（UNsaturated SOil hydraulic DAtabase）［9］。该数据库包含世界各地约790个土样的试验数据，并含有土的分类、试验方法、粒径分布、密度、饱和体积含水率、土样所处环境的温度及降雨量等内容。由于篇幅所限，分别选取该数据库中实验室试验条件下的黏土（clay）与砂土（sand）为研究对象进行曲线拟合。其中，黏土与砂土所包含的基质吸力－体积含水率的数据分别为23组及117组。

2.1.2 广西膨胀土及合肥膨胀土

UNSODA数据库中的数据主要是国外土样的试验结果。为了研究中国土体的SWCC曲线特征，经过查阅文献，得到了广西膨胀土的9组基质吸力－体积含水率数据［12－13］。

上述UNSODA中的数据及广西膨胀土的数据都是由文献中的资料收集而得的，其各组土样的具体取样地点、试验方法及试验条件都不相同。为了研究同一种土、同一种试验方法下SWCC的统计规律，以合肥市某工地的膨胀土为例，采用渗析法试验进行了6组重复试验，得到了6组相同试验条件下的基质吸力－体积含水率数据。

2.2 SWCC参数拟合结果

2.2.1 影响因素分析

1）拟合方法对SWCC参数的影响

分别采用3种拟合方法及FX1、FX2、FX3、VG1、VG2、VG3这6种模型对 UNSODA黏土、UNSODA砂土、广西膨胀土、合肥膨胀土进行SWCC参数拟合。大量数据的拟合结果表明：对于同一种SWCC模型，采用不同的拟合方法均能得到很好的拟合效果，但它们所得到的拟合参数不完全相同，某些参数值甚至相差较大。例如，表1是对UNSODA中第2361＃黏土采用FX2模型进行拟合的结果，各种拟合方法的拟合参数初值相同。表1中R2是决定系数，其表达式为：

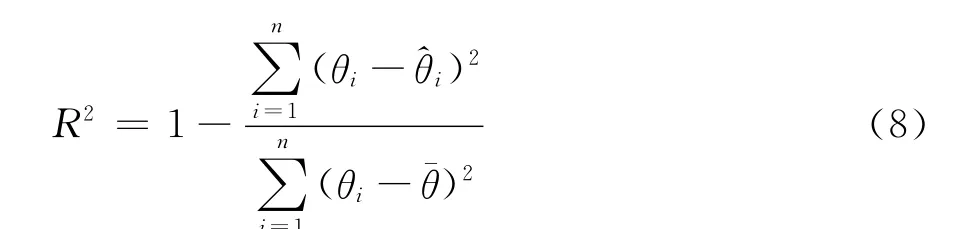
式中：θi及分别为第i个数据的实测值及预测值，为n个数据的平均值。

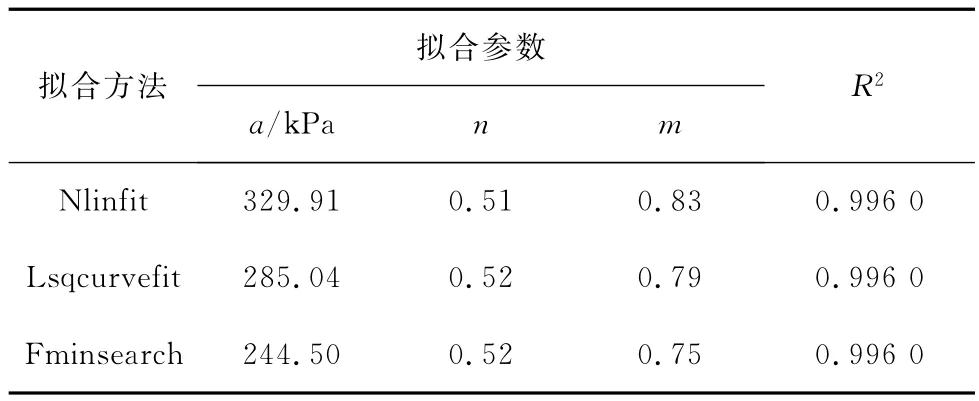
表1 UNSODA中2361＃黏土的SWCC拟合参数值（FX2）

由表1可见，3种拟合方法所得的拟合参数有一定差别，尤其是a值相差较大。但是，各种拟合方法的决定系数都大于0.99，这表明这3种拟合方法的效果都很好。图1为各种拟合方法所得的SWCC拟合曲线，可见，这3种拟合方法所得的SWCC拟合曲线几乎相同。因此，对于同一组吸力－体积含水率数据及同一种曲线拟合模型，采用不同的拟合方法可以得到不同的拟合参数值，但是它们都能较好地拟合原有数据。

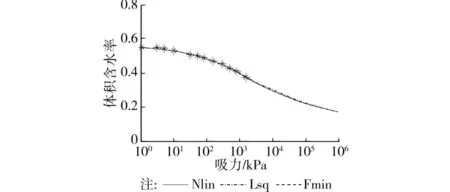
图1 UNSODA中第2361＃黏土的SWCC（FX2）

2）拟合模型对SWCC参数的影响

大量数据的拟合结果表明：拟合方法一定时，各种拟合模型所得的SWCC曲线参数亦有一定差异。图2是对UNSODA中第2361＃黏土采用Nlinfit进行拟合的结果。由图2（a）可知：FX1、FX2与FX3的差别主要在于高吸力部分。对于低吸力部分，它们的SWCC拟合曲线十分接近。由图2（b）可知，对于VG系列模型亦有此规律。

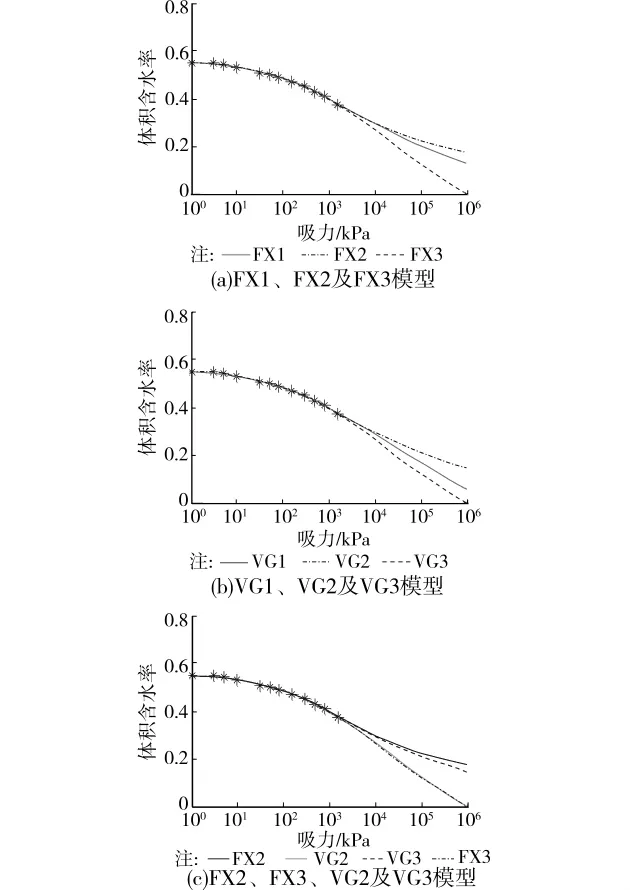
图2 UNSODA中第2361＃黏土的SWCC（Nlinfit）

图2（c）将FX2、FX3、VG2及 VG3的拟合曲线置于同一图形。尽管这4种模型的拟合参数有所不同，但由图2（c）可见，在低吸力部分，这4种模型的SWCC却十分接近；在高吸力部分，FX2与VG2的SWCC接近，FX3与VG3的SWCC几乎相同。

由于FX1及VG1都是4参数模型（参数：a、n、m、θr），而其它4个模型都是3参数模型（参数：a、n、m），因此，对于相同数目的试验数据点，FX1及VG1对应的拟合效果相对较差，有时会出现残余含水率为负的不合理现象。后续分析只对FX2、FX3、VG2及VG3模型进行研究。

2.2.2 SWCC参数的统计分析 为了研究SWCC曲线拟合参数的概率分布特征，基于上述研究，分别对采用FX2、FX3、VG2、VG3模型及3种拟合方法得到的参数a、n、m进行统计分析，求解UNSODA黏土、UNSODA砂土、广西膨胀土及合肥膨胀土的SWCC拟合参数的均值、均方差、变异系数、分布类型及参数间的相关系数。在进行参数的统计分析时，根据3倍均方差的原则进行异常数据的剔除。统计结果表明：UNSODA黏土及砂土的SWCC拟合参数满足对数正态分布；广西膨胀土及合肥膨胀土由于参与统计的数据组数偏少，未对其统计参数的概率分布类型。4种土的SWCC拟合参数均值统计结果见图3。

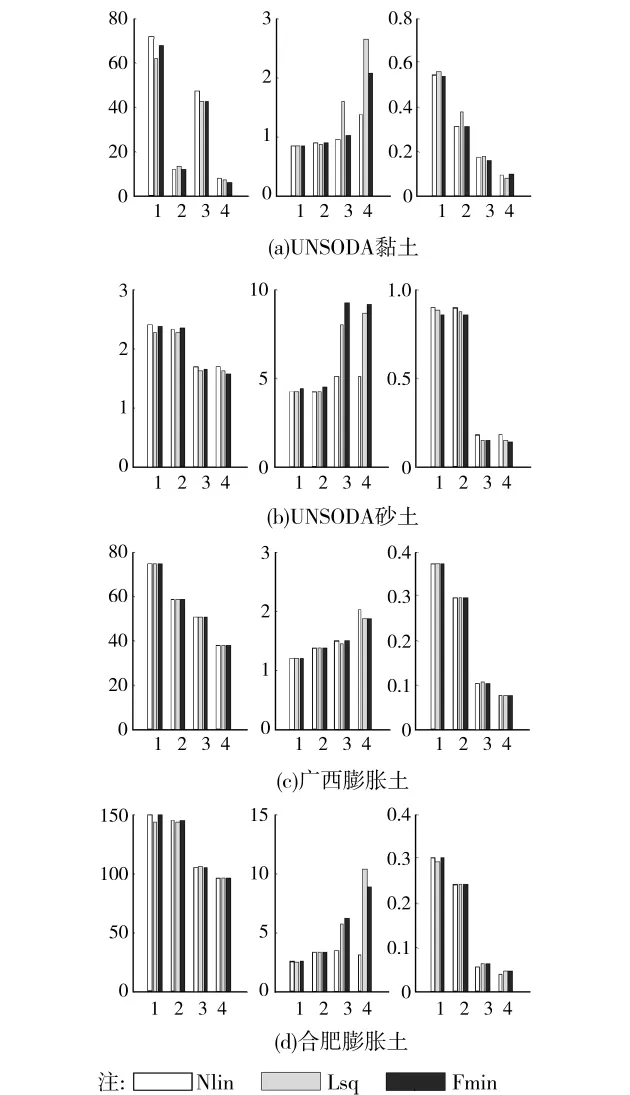
图3 SWCC拟合参数的均值

图3中，左、中、右图形分别代表参数a、n、m的统计结果；横坐标的数字1～4分别代表FX2、FX3、VG2及VG3模型；纵坐标代表参数a、n、m的均值，a的单位是kPa。

由图3可知：对于同一种土，SWCC拟合方法及拟合模型不同时，拟合参数值不同。但是，从统计意义上看，参数a、n、m的均值受拟合方法的影响不大，而受拟合模型的影响较大，即：拟合模型相同但拟合方法不同时，参数a、n、m的均值有一定变化，但相对变化量较小；拟合方法相同但拟合模型不同时，参数a、n、m的均值有较大变化。

对参数a、n、m的均方差及变异系数进行数理统计，亦可得出上述规律。为简化起见，文中只列出拟合方法2及模型FX2、VG2对应的拟合参数均值及变异系数，见表2～5。

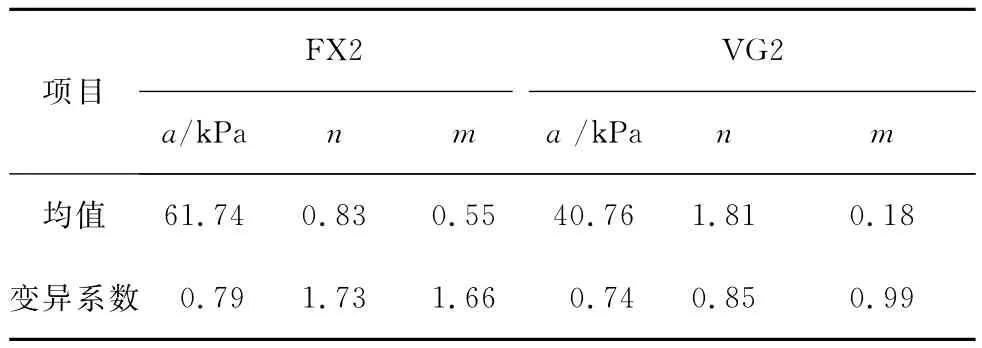
表2 UNSODA黏土的拟合参数（Lsqcurvefit）

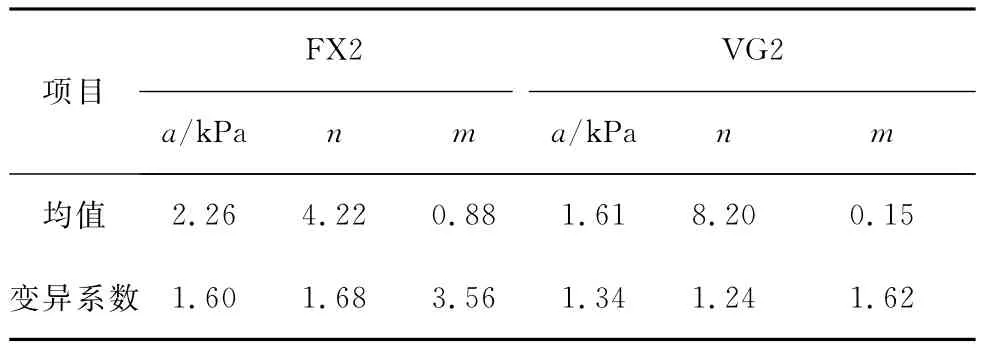
表3 UNSODA砂土的拟合参数（Lsqcurvefit）

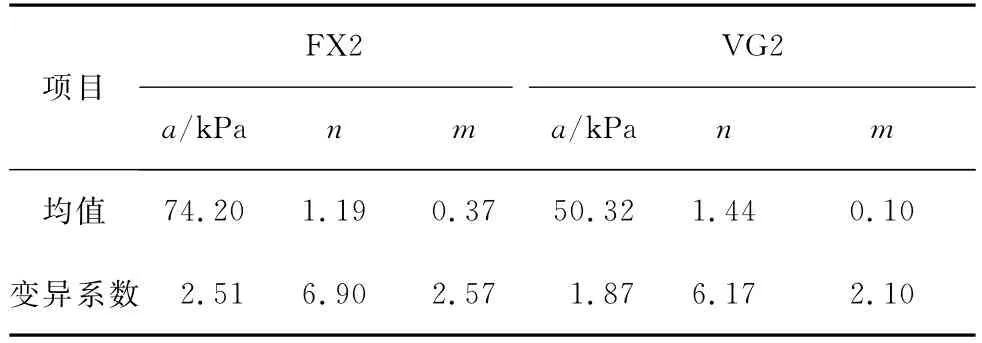
表4 广西膨胀土的拟合参数（Lsqcurvefit）

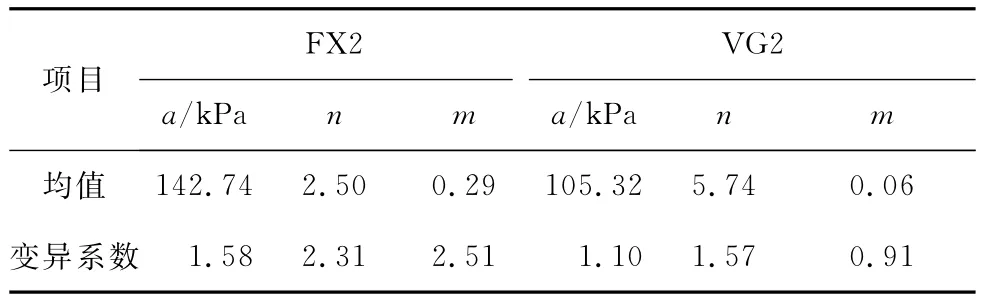
表5 合肥膨胀土的拟合参数（Lsqcurvefit）

以上述4种土的SWCC拟合均值为参数，可以绘制各种土的SWCC拟合曲线。例如，FX2模型的SWCC曲线如图4所示。由该图知：UNSODA黏土、广西膨胀土及合肥膨胀土的SWCC曲线形状较为一致，因为它们同属于黏土；相对于UNSODA砂土而言，它们的曲线相对平缓，曲线拐点不明显；而UNSODA砂土的SWCC曲线之斜率相对较大，曲线拐点相对较为明显。这种现象可结合表6进行解释。表6是对表2～5中FX2模型进行汇总得到的，它将UNSODA黏土、广西膨胀土及合肥膨胀土汇总为黏土，并统计了其拟合参数均值及变异系数的变化范围。由表6可见，对于均值而言，黏土的a值远大于砂土的a值，但黏土的n及m值却分别小于砂土的相应值；但对于变异系数而言，黏土与砂土的变异系数大小无明显区别。对表2～5中VG2模型进行统计，亦可同到类似的结论。

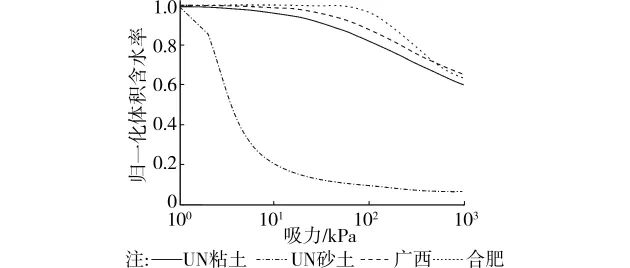
图4 SWCC拟合曲线（FX2模型，Lsqcurvefit）

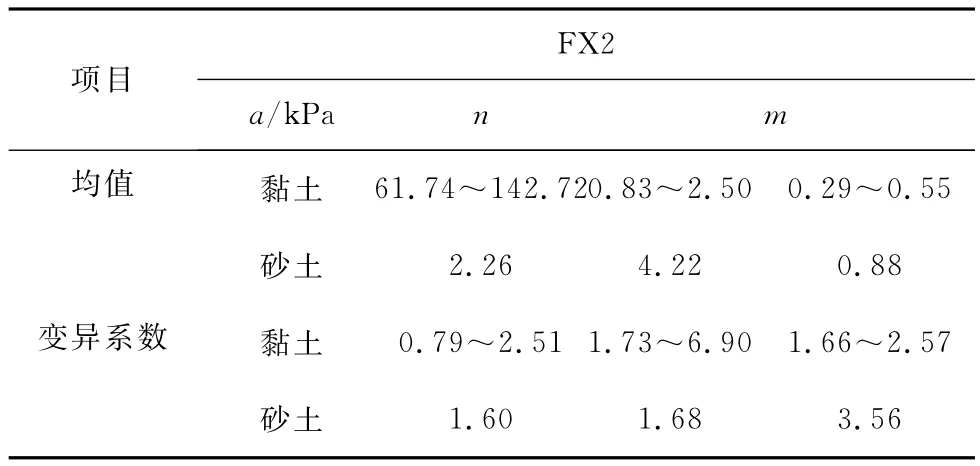
表6 黏土及砂土拟合参数对比分析（Lsqcurvefit）

2.2.3 SWCC参数的敏感性分析

为研究SWCC参数a、n、m对体积含水率θ的影响程度，判断各参数的相对影响，需要进行参数的敏感性分析。

参数的敏感性可以用因变量对自变量的导数来表示。在进行敏感性分析时，SWCC拟合参数为基本变量，饱和体积含水率为定值。为消除饱和体积含水率的影响，此处以归一化的体积含水率θn为研究对象进行参数的敏感性分析。

对于FX2模型，由式（1）可以推导出θn对3个拟合参数的导数公式如下：

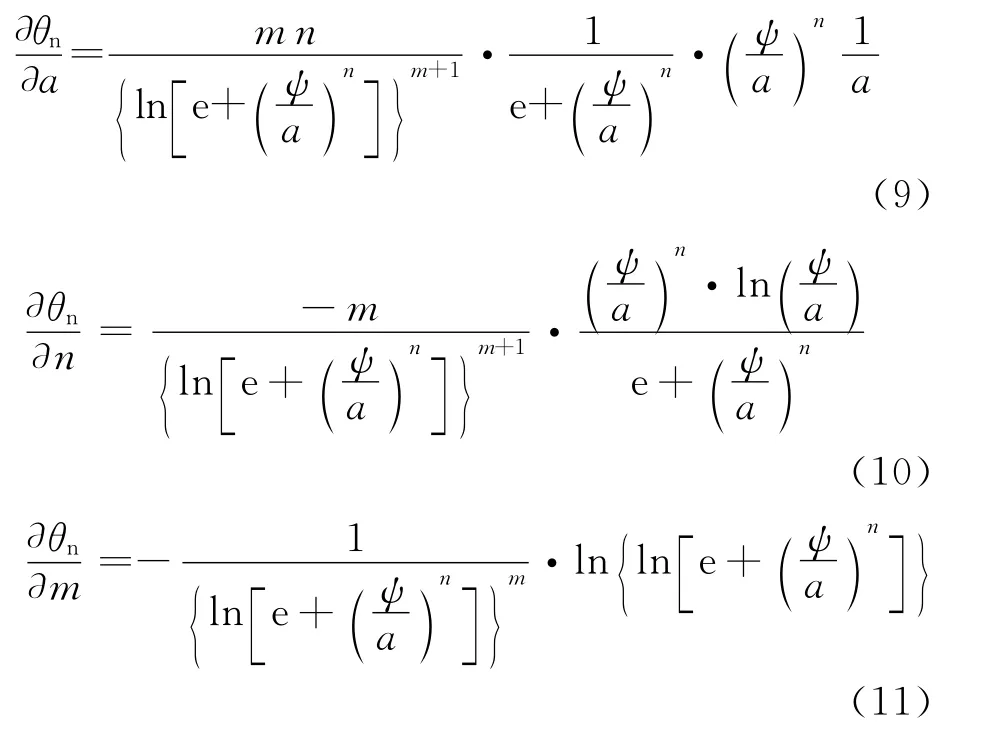
对于VG2模型，由式（5）可求得θn对3个拟合参数的导数公式为：

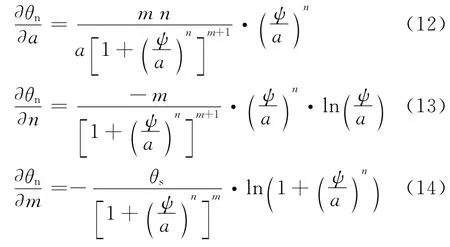
对于FX3及VG3模型，只需将式（9）～（14）分别乘以修正函数C（ψ），即可得到其对应的导数求解公式。

为了消除变量单位的影响，文［14］定义了无量纲化的敏感因子。对于系统特性P（X），X＝（X1，X2，…，Xn），敏感性因子的计算公式为：

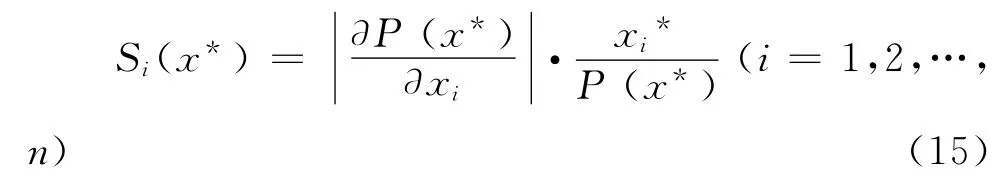
式中：x＊＝ （x1，x2，…，xn）＊为变量X的基准值。

当变量间具有相关性时，文［15］定义了可靠指标对参数均值的相对敏感性计算公式。借鉴这种方法，定义体积含水率对各参数的相对敏感性为：

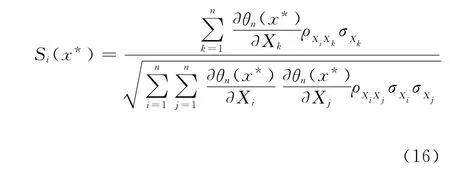
以FX2模型及UNSODA黏土为例，归一化体积含水率θn对3个变量的相对敏感性见图5。其中，图5（a）是假设变量间不相关时的敏感性曲线，图5（b）是根据参数a、n、m的统计结果（参数a与n、a与m、n与m间的相关系数分别为（0.36、0.48、0.33）计算而得的敏感性曲线，它考虑了参数间的相关性。由图5可见，对于UNSODA黏土，在工程常见的吸力范围内，θn对参数a的敏感性很小，对参数n、m的变化较为敏感；随着吸力的增加，θn对参数n的敏感性逐渐减小，敏感性数值由正转负；θn对参数m的敏感性数值为负值，其绝对值在60kPa左右达到最大值；参数间的相关性对参数a的敏感性有较大影响，但对参数n及m的敏感性影响不大。

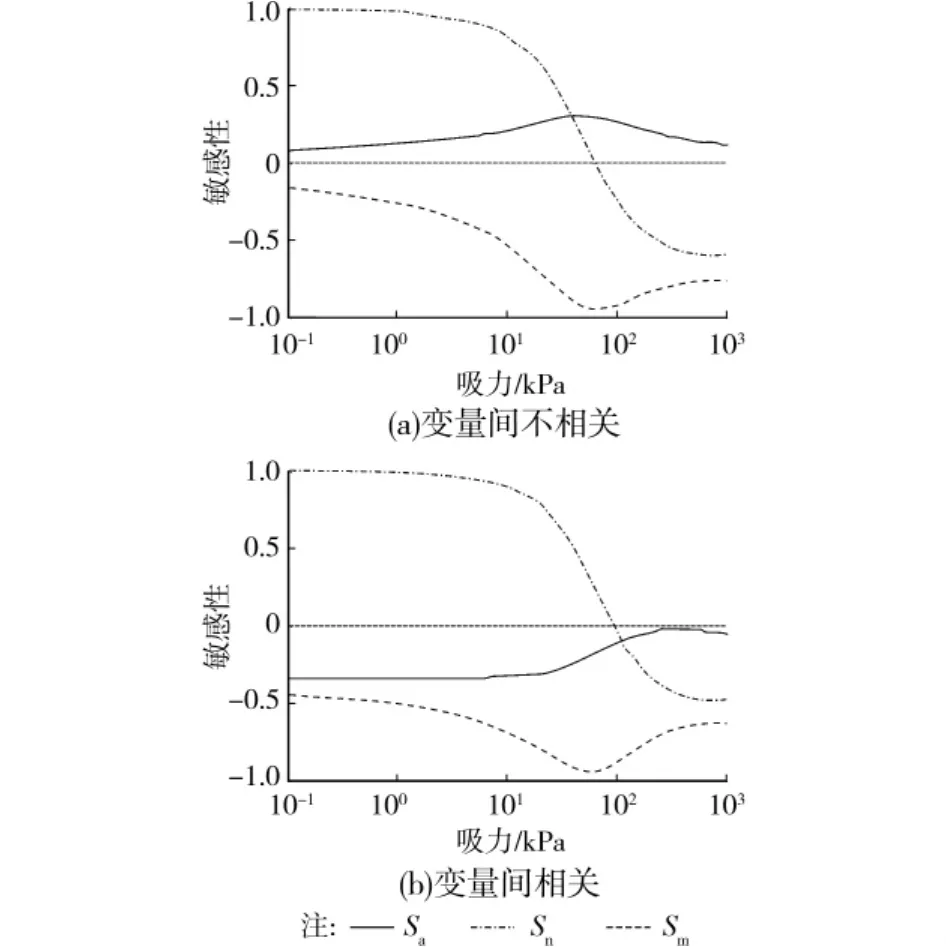
图5 归一化体积含水率对SWCC参数的敏感性（UNSODA黏土）

3 结 论

以Fredlund－Xing模型的3种型式（FX1、FX2、FX3）及van Genuchten模型的3种型式（VG1、VG2、VG3）为SWCC曲线的拟合模型，以科学计算语言 Matlab中的3种函数（Nlinfit、Lsqcurvefit、Fminsearch）为拟合方法，对UNSODA数据库中的黏土与砂土、广西膨胀土及合肥膨胀土的大量基质吸力－体积含水率数据进行了曲线拟合，得到了这4类土的拟合参数均值、均方差、变异系数、分布类型及参数间的相关系数；求得了这4种土的典型SWCC曲线；提出了归一化体积含水率对SWCC曲线参数的相对敏感性计算公式，进行了参数的敏感性分析。这些研究成果为非饱和土工程的可靠度分析提供了必要的研究基础。

计算结果表明：

1）拟合方法对SWCC拟合参数有一定影响，不同的拟合方法可以得到不同的拟合结果；但从统计意义而言，大量拟合参数的均值、均方差及变异系数受拟合方法的影响不明显。

2）拟合模型对SWCC拟合参数影响较大，采用不同的拟合模型可以得到不同的拟合参数。对于相同数目的数据点，FX2、FX3、VG2、VG3的拟合效果优于FX1及VG1；FX2、FX3、VG2与VG3在低吸力部分的SWCC曲线一致；在高吸力部分，FX2与VG2的SWCC接近，FX3与VG3的SWCC接近。

3）UNSODA黏土、广西膨胀土及合肥膨胀土同属于黏土，其SWCC曲线形状较为一致，它们的a值一般较大，n值相对较小，曲线拐点不明显，曲线中部的斜率较小。UNSODA砂土的a值较小，n值较大，曲线拐点较为明显，曲线的斜率相对较大。

4）敏感性分析结果表明：参数a对归一化体积含水率θn的影响程度较小，θn对参数a的变化不敏感，而对参数n及m的变化则较为敏感。

［1］周葆春，孔令伟，陈伟，等.荆门膨胀土土－水特征曲线特征参数分析与非饱和抗剪强度预测［J］.岩石力学与工程学报，2010，29（5）：1052－1059.ZHOU Baochun，KONG Lingwei，CHEN Wei，et al.Analysis of characteristic parameters of soil－water characteristic curve（SWCC）and unsatureated shear strength prediction of Jinmen expansive soil ［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29（5）：1052－1059.

［2］Miao L C，Houston S L，Cui Y，et al.Relationship between soil structure and mechanical behavior for an expansive unsaturated clay［J］.Canadian Geotechnical Journal，2007，44：126－137.

［3］Nuth M，Laloui L.Advances in modelling hysteretic water retention curve in deformable soils ［J］.Computers and Geotechnics，2008，35（6）：835－844.

［4］Pedroso D M，Williams D J.A novel approach for modelling soil－water characteristic curves with hysteresis［J］.Computers and Geotechnics，2010，37（3）：374－380.

［5］林鸿州，于玉贞，李广信，等.土水特征曲线在滑坡预测中的应用性探讨［J］.岩石力学与工程学报，2009，28（12）：2569－2576.LIN Hungchou，YU Yuzhen，LI Guangxin，et al.On application of soil－water characteristic curves to landslide forecast ［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（12）：2569－2576.

［6］Nam S，Gutierrez M，Diplas P，et al.Comparison of testing techniques and models for establishing the SWCC of riverbank soils ［J］.Engineering Geology，2009，110（1／2）：1－10.

［7］Sillers W S，Fredlund D G，Zakerzadeh N.Mathematical attributes of some soil－water characteristic curve models［J］.Geotechnical and Geological Engineering，2001，19：243－283.

［8］Puppala A J，Punthutaecha K，Vanapalli S K.Soilwater characteristic curves of stabilized expansive soils［J］.Journal of Geotechnical and Geoenvironmental Engineering，2006，132（6）：736－751.

［9］Phoon K K.Santoso A，Quek S T.Probabilistic analysis of soil－water characteristic curves［J］.Journal of Geotechnical and Geoenvironmental Engineering，2010，136（3）：445－455.

［10］Fredlund D G，Xing A.Equations for the soil－water characteristic curve ［J］.Canadian Geotechnical Journal，1994，31：521－532.

［11］van Genuchten M T.A closed form equation predicting the hydraulic conductivity of unsaturated soils［J］.Soil Science Society of America Journal，1980，44：892－898.

［12］孔令伟，李雄威，郭爱国，等.脱湿速率影响下的膨胀土工程性状与持水特征初探 ［J］.岩土工程学报，2009，31（3）：335－340.KONG Lingwei，LI Xiongwei，GUO Aiguo，et al.Preliminary study on engineering behaviors and water retention characteristics of expansive soil under influence of drying rate ［J］.Chinese Journal of Geotechnical Engineering，2009，31（3）：335－340.

［13］谭波，郑健龙，余文成.降雨条件下膨胀土路堑边坡渗流分析［J］.中外公路，2009，29（2）：28－32.TAN Bo，ZHENG Jianlong，YU Wencheng.Seepage analysis of expansive soil cutting slope subjected to rainfall infiltration［J］.Journal of China and Foreign Highway，2009，29（2）：28－32.

［14］朱维申，何满潮.复杂条件下围岩稳定性与岩体动态施工力学［M］.北京：科学出版社，1995，128－144.

［15］谭晓慧，王建国，刘新荣，等.边坡稳定的有限元可靠度计算及敏感性分析［J］.岩石力学与工程学报，2007，26（1）：115－122.TAN Xiaohui，WANG Jianguo，LIU Xinrong，et al.Finite element reliability computation and sensitivity analysis of slope stability［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（1）：115－122.