巨型钢框架复合支撑体系拉索直径确定方法

唐柏鉴，顾 盛，刘和平

（1.江苏科技大学 土木工程系，江苏 镇江212003；2.重庆华发建筑工程有限公司，重庆401120）

1 巨型钢框架预应力复合支撑体系

为缓解巨型桁架节点受力集中、提高巨型框架的抗侧刚度，作者提出了巨型钢框架预应力复合支撑体系［1－2］（ZL200720045216.5 及 ZL200710131100.8）。刚性八字支撑与倒八字柔性拉索组合形成刚柔兼济的复合支撑系统，既参与抗侧，同时将巨型梁竖向荷载以轴力形式通过巨型柱传递至基础，如图1所示。

拉索直径的确定是预应力钢结构的关键问题之一［3－9］。巨型钢框架预应力复合支撑体系属于巨型结构与预应力钢结构的综合应用，子结构可悬挂可座承，起减振耗能作用［10］。分别从力学平衡角度和变形协调角度，建立该体系拉索直径的确定方法。

图1 巨型钢框架预应力复合支撑体系

2 机理分析

2.1 水平荷载引起复合支撑内力不平衡

以单大层结构为例，通过水平荷载下结构脱离体平衡方程分析，剖析复合支撑内力不平衡的原因。本文中若无特殊说明，则八字支撑内力及内力增量均以压为正，拉索内力及内力增量均以拉为正。

2.1.1 水平集中力引起的复合支撑内力不平衡

水平及重力下的结构如图2、3所示。上半部分由巨型八字支撑及巨型钢框架共同抵抗水平集中荷载，下半部分由拉索及巨型钢框架共同抵抗水平集中荷载。

图2 反对称水平集中荷载作用图

图3 W作用下结构变形增量图

水平集中荷载下脱离体横向受力分析如图4（a）（AC段剖切）、图4（b）（CE段剖切）所示。

图4 水平集中荷载下脱离体受力分析

图4中，NW表示在水平集中荷载W作用下八字支撑的内力增量，PW表示在集中水平荷载W作用下拉索的内力增量，QWU表示水平集中荷载W作用下巨型柱上半段剪力增量，QWD表示水平集中荷载W作用下巨型柱下半段剪力增量。

八字支撑中的剪力相对于轴力可忽略不计，因此在脱离体中未画出。

由水平集中荷载下脱离体横向受力分析，列出水平方向力学平衡方程：

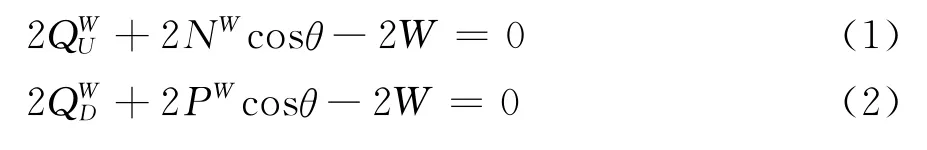
八字支撑与拉索都属于斜向抗侧力构件，在抗侧能力上相对于钢框架是强者，两个强者各自分担的水平荷载在同一量级。实际工程中，八字支撑的截面积大于拉索的截面积，因此八字支撑的内力增量NW大于拉索的内力增量PW。

即水平集中力作用下，八字支撑的内力增量大于拉索内力增量，两个增量的差值与拉索截面积的相对大小相关。

2.1.2 水平均布荷载引起的复合支撑内力不平衡水平均布荷载下的结构如图5、6所示。

图5 反对称水平均布荷载作用图

图6 f作用下结构变形增量图

1）上半部分

反对称水平均布荷载下，下半部分水平均布荷载对结构上半部分的影响可忽略不计，将结构下半部分简化为弹簧支座（图7），取结构上半部分进行受力分析。

水平均布荷载下上半柱的简化力学模型如图8所示。

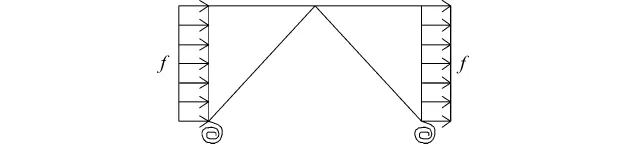
图7 上半部结构受力图

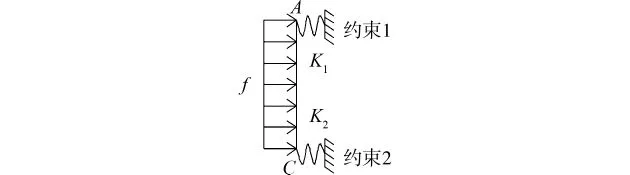
图8 上半柱简化力学模型

对上半柱简化力学模型进行受力分析，可得上半柱的剪力增量图（图9（a））。

图9 上半部水平均布荷载下脱离体受力分析

将结构上半部分在A、B、C3处截开，对脱离体进行横向受力分析（图9（b）、（c）、（d）），并列出水平方向力学平衡方程：

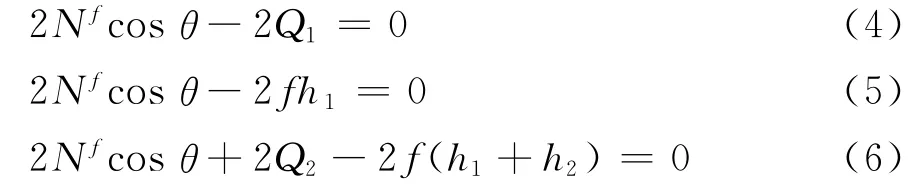
2）下半部分

反对称水平均布荷载下，结构下半部分受到CE段水平均布荷载作用以及由结构上半部分传来的内力作用（图10）。

图10 下半部结构受力图

水平均布荷载下下半柱的简化力学模型如图11所示。由于结构上半部分的内力FV对巨型柱CE段的剪力增量及拉索内力增量影响很小，因此在简化力学模型中未画出。

对图11（b）所示简化力学模型进行受力分析，可得下半柱在FH及M作用下的剪力增量图（图12（b）），剪力增量Q5主要是由FH引起的。

对图11（c）所示简化力学模型进行受力分析，可得下半柱在CE段水平均布荷载f作用下的剪力增量图（图12（c）），C点的剪力增量为Q6，E点的剪力增量为Q7。

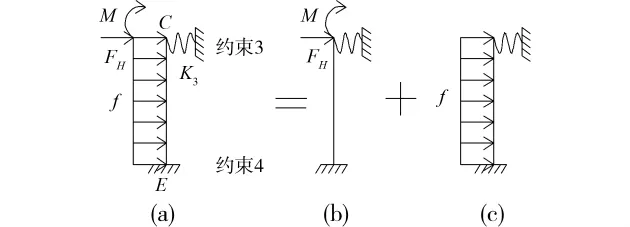
图11 下半柱简化力学模型

为控制结构下半部分的侧移，拉索截面积不能过小，要求拉索的抗侧能力是钢框架的数倍。因此通常情况下：

叠加图12（b）与图12（c）得结构在水平均布荷载下的下半柱剪力增量图（图12（a）、图13（a））。

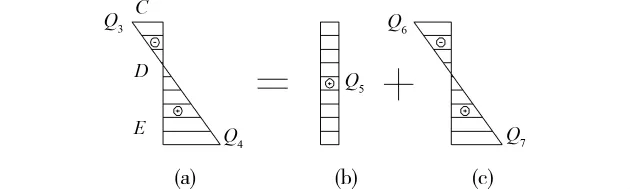
图12 下半柱剪力增量叠加

图13 下半部水平均布荷载下脱离体受力分析

将结构下半部分在C、D、E3处截开，结合下半柱剪力增量图（图13（a）），对脱离体进行横向受力分析（图13b，c，d），并列出水平方向力学平衡方程：

将式（9）减去式（5），得：

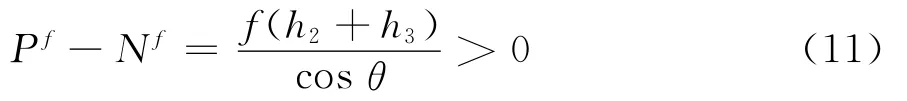
在反对称水平均布荷载下，拉索的内力增量大于八字支撑的内力增量，两个增量的差值与拉索截面积的相对大小相关。

2.2 复合支撑内力差值调平

在水平集中荷载作用下八字支撑的内力增量大于拉索的内力增量，左侧复合支撑的内力差值与右侧反对称；在水平均布荷载下拉索的内力增量大于八字支撑的内力增量，左侧复合支撑的内力差值与右侧亦为反对称。若采用对拉索施加预拉力进行调节，由预拉力产生的内力差值是左右对称的，因此当左侧复合支撑内力平衡时，右侧复合支撑的内力差值扩大为原来的两倍。所以，由反对称水平荷载引起的左右反对称的内力差值只能通过另一组左右反对称的差值来调平，即由反对称荷载引起的复合支撑之间的内力差值只能通过反对称手段来调平。

从上述推导过程可知，由水平集中荷载引起的复合支撑内力差值及由水平均布荷载引起的复合支撑内力差值均可通过改变拉索截面积来调节其大小，且上述两个差值反号，因此采用调节拉索截面积的方法可实现复合支撑内力平衡。换言之，拉索截面积的大小由反对称水平荷载决定。

对于n大层结构，顶部第n大层仅受到水平均布荷载作用，因此，顶部第n大层在水平均布荷载作用下拉索的内力增量大于八字支撑的内力增量，且无法调平，只能尽可能取用较小截面的拉索，以尽可能降低复合支撑内力差值。而下部各大层，除了受到作用在本大层的水平均布荷载作用外，还受到相邻上部大层根部传来的水平集中荷载作用，因此下部各大层具有调平的条件。

3 拉索直径确定方法

任意多大层结构体系，在竖向荷载的基础上施加水平均布荷载f，假设各大层水平均布荷载相等。因此除顶大层仅承受水平均布荷载外，其余各大层同时受有本大层的水平均布荷载和来自于上部结构的水平集中力。依据上述机理分析，可以通过调节各大层拉索截面积，实现水平荷载下复合支撑内力平衡。

将第i大层拉索的初始截面积记为Ai，其增量记为ΔAi。

顶部大层由于仅受到作用在本大层的水平均布荷载作用，只能通过调节拉索截面积An来减小复合支撑内力差值，而无法达到内力平衡。在调平方程中需要给定一个合适的差值Zn，根据大量数值分析经验［11］，可取Zn为：

其中h为巨型层高度，θ为复合支撑与水平线夹角。

若要复合支撑内力平衡则需满足：

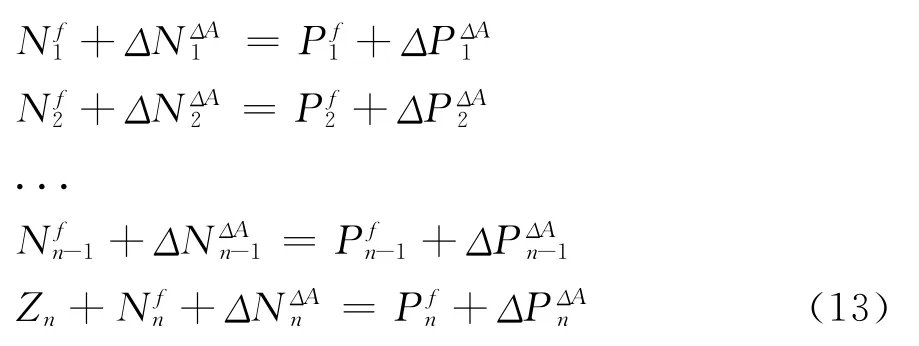
上述方程中Nfi和Pfi是指在水平荷载f作用下第i大层复合支撑的内力增量。ΔNΔAi和ΔPΔAi则表示拉索截面积变化引起的第i大层复合支撑内力增量。

其中，所有大层的拉索截面积同时变化，其引起的复合支撑的内力变化，可近似等于各大层拉索截面积单独变化，引起的复合支撑的内力变化之和。即：

因此，式（13）可改写为：

为了方便求解调平方程，将ΔPΔAii记为Xi。用αij表示第i层拉索截面积增加ΔAi时（i层拉索内力增量的变化量为Xi），第j层八字支撑内力增量的变化量比例系数；用βij表示第i层拉索截面积增加ΔAi时（i层拉索最终内力增量的变化量为Xi），第j层拉索内力增量的变化量比例系数。将αij、βij定义为影响系数。

则上述方程组改写为：

利用方程组（17）可解出第i层拉索内力增量的变化量为Xi。在既定水平荷载下，第i层拉索内力增量Pi与拉索截面积Ai成非线性关系。因此需要通过插值求得调平所需的ΔAi，使得第i层拉索截面积增量为ΔAi时，第i层拉索内力增量的改变量为Xi。

由于方程（14）、（15）做了近似处理，因此经过一次计算所得的ΔAi只是接近于真实值。按ΔAi改变原拉索截面积后，在水平均布荷载f下各大层复合支撑仍存在内力差值，但内力差值比未调节前明显减小。在上一次计算结果的基础上进行迭代计算，将拉索截面积按上一次的计算结果进行修正后再用影响系数法继续计算。前后2次计算中的影响系数在数值上存在较小的差别，因此影响系数也需重新计算。经验表明，迭代2～3次后内力差值就已满足工程要求。

本文将上述方法命名为影响系数迭代调平法。

4 数值算例

巨型钢框架复合支撑体系SAP2000计算模型如图1所示，平面尺寸36m×36m，总高216m，共54层，层高4m。结构四角为6m见方的格构式巨型柱，每个巨型柱由四根箱形截面柱，通过柱间人字形支撑相连而成。在第9层、18层、27层、36层、45层和54层各设置四根巨型梁与巨型柱相连，每个巨型梁为一个楼层高，由四根工字形弦杆与竖向、斜向支撑组合而成。每个巨型梁下，设置4层高的巨型八字支撑，巨型八字支撑也是由4根工字形弦杆与支撑腹杆组合而成。同时在巨型八字支撑与下一层巨型梁之间设置预应力拉索。主要构件尺寸如表1所示，初始分析时各层拉索截面积相同。

梁柱杆件采用空间柱单元模拟，楼板单元采用四节点板壳单元模拟。预应力拉索由索单元模拟，由于拉索不受弯、不受扭，惯性矩修正系数为1%，采用负温度模拟拉索的预拉力。考虑几何大变形［12］。

主结构各层恒载6.0kN／m2，活载2.5kN／m2，子结构各层恒载4.5kN／m2，活载2.5kN／m2，将子结构简化成均布荷载作用在巨型梁上。在竖向荷载下通过调节拉索预拉力将复合支撑的内力调平（图14），然后施加自左向右的水平均布荷载，设定3种级别：f1＝6kN／m2，f2＝9.2kN／m2，f3＝12kN／m2。

底大层至顶大层的拉索分别记为c1至c6；八字支撑分别记为b1至b6。

表1 数值模型的截面尺寸

如图14可见，施加水平荷载f2后，复合支撑内力不再平衡。对于右侧复合支撑，第1至第3大层的拉索内力增量明显小于八字支撑内力增量，第4大层的拉索内力增量与八字支撑内力增量基本相等，第5大层的拉索内力增量大于八字支撑内力增量。左侧支撑可同理分析。

采用影响系数迭代法对拉索直径进行调节，首次计算中的影响系数如图15所示。

影响系数在拉索截面积增大处设定为1，其余各处的影响系数均为负且是小量。离拉索截面积增大处越远，影响系数的绝对值就越小。

以图15（d）为例。增大A4使c4的内力增量增大；增大A4相当于第4大层K型节点处对上部结构的约束增强，使上部钢框架的相对抗侧刚度略有增大，由复合支撑所分担的水平荷载略有减小，因此上部结构中复合支撑的内力增量略有减小，离c4越远复合支撑内力增量的变化量越小；增大A4使第4大层根部传递给第3大层的集中弯矩减小，因此下部各大层的复合支撑内力增量略有减小，离c4越远复合支撑内力增量的变化量越小。其他可同理分析。

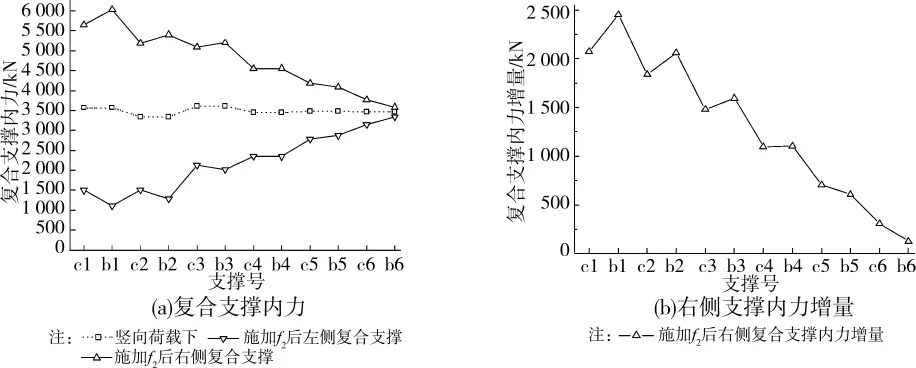
图14 施加水平荷载后复合支撑内力

图15 影响系数曲线

经3次迭代计算后，各大层拉索直径如表2所示，此时水平荷载f2作用下复合支撑内力实现了平衡（图16）。改变水平荷载的大小，在水平荷载f1及f3下，复合支撑仍然保持内力平衡（图16），只是内力大小随外荷载大小发生了变化。

表2 复合支撑内力平衡时的拉索直径

图16 水平均布荷载下复合支撑内力调平

调平后，每大层的左右复合支撑形成2个对称的内力平台，其对称轴为竖向荷载下复合支撑内力平衡时的内力基准线（图16（a）），左侧复合支撑的内力平台在对称轴下方，右侧复合支撑的内力平台在对称轴上方。右侧复合支撑的内力增量平台从上至下逐层升高（图16（b）），这说明水平荷载从上至下具有累积效应。左侧支撑反之。

5 结 论

通过对水平荷载下巨型钢框架复合支撑体系的受力机理分析，研究了水平荷载作用下，复合支撑内力不平衡的原因和拉索直径的决定因素，建立了拉索直径的确定方法，并通过数值算例验证。主要结论如下：

1）水平荷载下，由于巨型结构每大层的上、下半段抗侧刚度不同，进而巨型柱上、下段剪力不同，导致复合支撑内力不平衡。

2）反对称荷载下的复合支撑内力不平衡，只能采用反对称手段调平，即通过调节拉索直径，实现反对称水平荷载下的复合支撑内力平衡。

3）拉索直径由反对称水平荷载决定，以在竖向荷载的基础上施加水平荷载，复合支撑内力平衡为准则。

4）建立的影响系数迭代调平方法确定拉索直径，具有良好的精度和可操作性。

［1］唐柏鉴，阮含婷.附加阻尼装置的悬挂式巨型钢框架支撑体系模态分析［J］.江苏科技大学学报，2008，22（4）：18－23.TANG Baijian，RUAN Hanting.Modal analysis of mega－frame－brace－suspended structure with damper［J］.Journal of Jiangsu University of Science and Technology，2008，22（4）：18－23.

［2］唐柏鉴，阮含婷.巨型钢框架预应力复合支撑体系性能初探［J］.广西大学学报，2010，35（4）：574－581.TANG Baijian，RUAN Hanting.Analysis on performance of mega steel frame and prestressed composite brace structure［J］.Journal of Guangxi University，2010，35（4）：574－581.

［3］Chan S L，Shu G P，Lyu Z T.Stability analysis and parametric study of pre－stressed stayed columns ［J］.Engineering Structures，2002，24：115－124.

［4］Kang W J，Chen Z H，Lam H F，et al.Analysis and design of the general and outmost－ring stiffened suspendome structures［J］.Engineering Structures，2003，25（13）：1685－1695.

［5］Yuan X F，Chen L M，Dong S L.Prestress design of cable domes with new forms［J］.International Journal of Solids and Structures，2007，44：2773－2782.

［6］Wang Z H，Yuan X F，Dong S L.Simple approach for force finding analysis of circular Geiger domes with consideration of self－weight ［J］.Journal of Constructional Steel Research，2010，66：317－322.

［7］Cao Q S，Zhang Z H.A simplified strategy for force finding analysis of suspendomes ［J］.Engineering Structures，2010，32（1）：306－318.

［8］任俊超，张其林，童丽萍.预张力值对郑州会展中心斜拉结构的稳定性能影响分析［J］.工业建筑，2008，38（5）：100－103.REN Junchao，ZHANG Qilin，TONG Liping.Influence of pre－tension on stability performance of spatial stay structure for Zhengzhou Conference and Exhibition Center ［J］.Industrial Construction，2008，38（5）：100－103.

［9］Xue W C，Liu S.Design optimization and experimental study on beam string structures ［J］.Journal of Constructional Steel Research，2009，65：70－80.

［10］唐柏鉴，王治均.大跨网格屋盖结构竖向 MTMD减震控制的参数分析［J］.工程力学，2009，26（5）：130－136.TANG Baijian，WANG Zhijun.Parametric analysis of vertical MTMD in long－span lattice roof structures［J］.Engineering Mechanics，26（5）：130－136.

［11］顾盛.新型竖向预应力钢结构体系拉索截面积及预拉力确定理论［D］.江苏科技大学，2012.

［12］唐柏鉴，朱晶晶.撑杆式预应力钢压杆最佳初始预拉力完备理论解［J］.工程力学，2011，28（9）：143－148.TANG Baijian，ZHU Jingjing.Perfect theoretical equation of optimum initial prestress of stayed steel column［J］.Engineering Mechanics，2011，28（9）：143－148.