钢筋高应变低周疲劳寿命的统计分析
盛光敏,薛昊飞,吕煜坤
(重庆大学 材料科学与工程学院,重庆400044)
目前,全球已处于地震活跃期。由于地震对建筑物有巨大的破坏作用,因此对建筑材料的性能要求越来越高[1-2]。目前广泛采用的钢筋混凝土结构由具有一定延性的钢筋和完全脆性的混凝土组成,其中钢筋起到加强的作用[3]。在地震过程中,钢筋所承受的是高应变交变载荷,其失效形式以高应变低周疲劳为主[4],所以高应变低周疲劳性能是钢筋的主要抗震性能指标。
疲劳寿命具有较大的分散性,因此采用合理的数据统计处理方法来提供可靠的疲劳失效数据是疲劳研究领域的热点之一。多年来学者们处理疲劳实验数据的方法很多,对不同应力水平下的高周疲劳实验数据,通常采用升降法、S-N曲线法、Duezt数理处理等[5]数理统计方法处理疲劳性能数据;对滚动接触疲劳试验下所得到的疲劳数据,通常采用威布尔双参数分布[6]方法;对不同应力或低应变水平下的低周疲劳实验数据,通常运用灰度预测模型、有限元分析进行仿真[7-8]。但是对于抗震钢筋高应变水平下的低周疲劳的实验数据处理,目前还没有研究报道,因此本文对这一方面进行了对比研究,运用不同的统计方法处理数据,使评价钢筋的高应变低周疲劳性能更科学、更合理,为地震设防区建筑结构的设计提供依据。
1 试验方法
由于采用轧后淬火、自回火的方法生产钢筋,投资少、成本低、经济效益良好,世界很多国家都在普遍采用[9-10]。中国轧后淬火、自回火钢筋也投入生产应用有20余年的历史[11],所以本试验选用轧后淬火、自回火的HRB400QST,其化学成分如表1所示。

表1 钢筋化学成分 wt%
考虑到轧后淬火、自回火工艺会使钢筋表层形成马氏体,心部形成铁素体和珠光体[11],将其加工成标准的低周疲劳试样时表层的马氏体组织会被磨削掉。这时试样就不具备原始的力学性能。因此实验时,全部试样均未经过任何机械加工处理,且规格全为Φ16mm,如图1所示。

图1 低周疲劳试样示意图(表面未加工)
疲劳试验的设备是Instron Model1342液压伺服材料试验机。在大气环境室温下,采用恒定总应变控制,利用标注为12.5mm的轴向引伸计(如图2)控制总应变范围Δεt,在4个应变幅下进行,分别为±0.5%、±1%、±1.5%、±2%,通过模拟 数字转换器,用计算机自动采集响应数据。其中循环波型为正弦波,加载频率为0.1-0.4Hz,应变循环比Rε=-1。
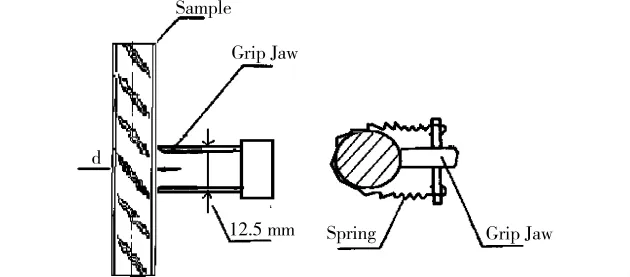
图2 轴向引伸设置
2 低周疲劳寿命测试结果
试验为完全失效试验,样本数量为每组6个,所得数据如表2。
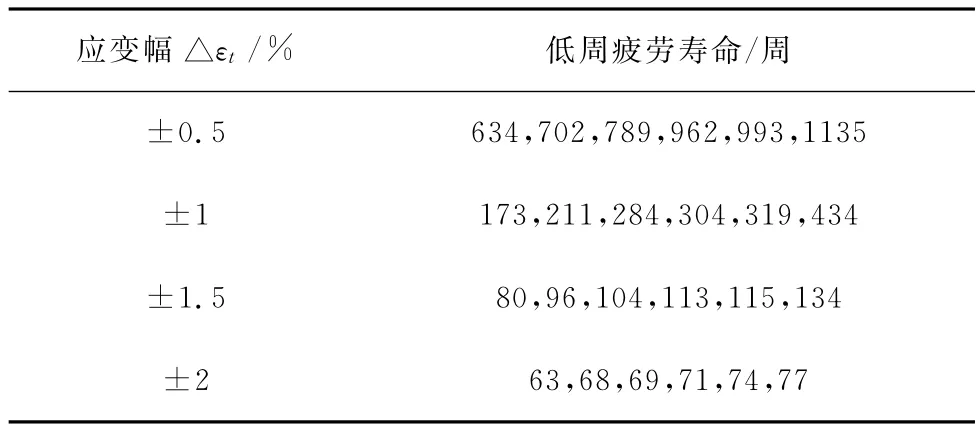
表2 疲劳试验的结果
从表2中可以看出,由于试验过程中存在着诸多不确定性因素,如材料成分不均匀、试样表面状况的差异等,试样的疲劳寿命分散性较大。因此采用了多种常用的的统计方法分别对疲劳数据进行了分析计算。
3 低周疲劳寿命的统计处理
3.1 双参数威布尔分布
威布尔分布是随机分布函数之一,广泛应用于各种寿命试验的数据处理[12-13],因此假设疲劳实验数据符合双参数威布尔分布。
双参威布尔分布函数为:
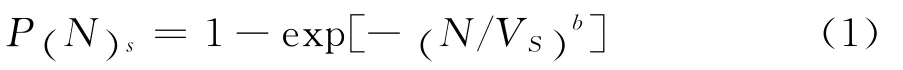
其对数形式:
聚类分析的结果能够反应高频关键词间的亲疏关系,揭示当期研究热点[7]。从图3聚类分析的部分结果可以看出,当前创客教育的主要研究内容如下。
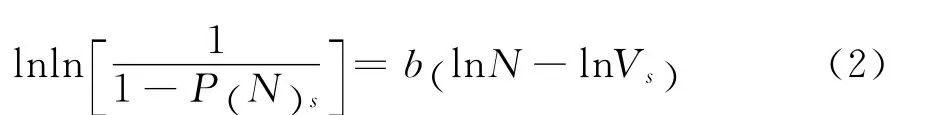
式(1)和(2)中:P(NS)是在某一试验应变水平下,试样寿命小于N的概率;N表示试样寿命(周次);b表示威布尔分布的斜率参数,代表数据的分散度,其值越大数据分散性越小;VS表示威布尔分布的特征寿命(失效率为63.2%时的疲劳寿命);1-P(NS)为试样大于寿命N,即不失效的概率,定义为置信度。
采用最大似然方法或最佳线性不变估计方法确定b和VS。本实验是完全失效试验,对试验所得的6个疲劳寿命从小到大排列(N1<N2<N3<……<Ni)。
1)最大似然方法关于b和VS的计算公式为:

其中需要对斜率参数b修正偏差,修偏系数g可查国家标准GB 10622-89中表得之:b=g·。由(3)计算b和VS结果见表3。
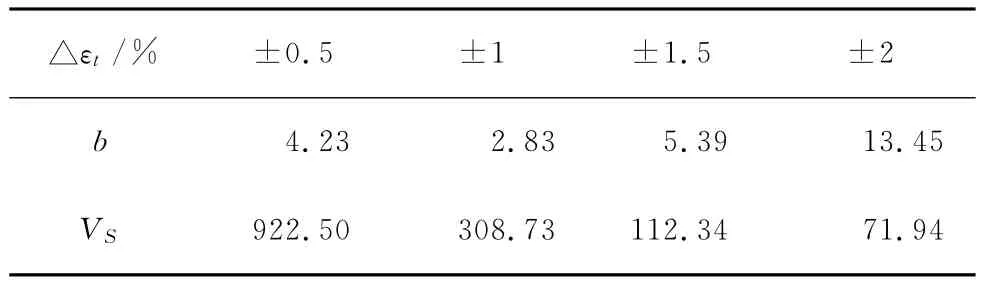
表3 不同应变下b和VS的值
将表3的结果代入式(1)得出的不同置信度下疲劳寿命如图3所示:
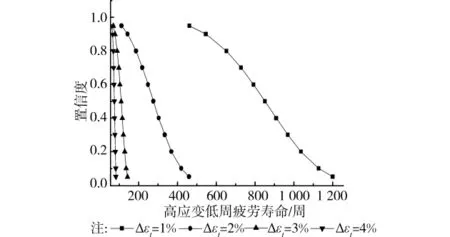
图3 疲劳寿命 置信度关系曲线(最大似然法)
2)最佳线性不变估计关于b和VS的计算公式为:

式(4)中CI和DI为最佳线性不变估计系数,可查国家标准GB 10622-89表得之。由(4)计算b和VS结果见表4。

表4 不同应变下b和VS的值

图4 疲劳寿命 置信度关系曲线(最佳线性法)
3.2 正态分布与对数正态分布
试验疲劳寿命的样本为Ni,正态分布的概率密度函数为:
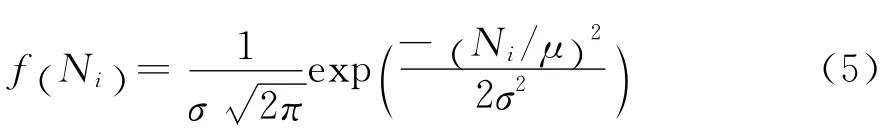
依参数估计中点估计或最大似然法均可知期望

式(6)中P(NS)为置信度。根据不同概率所得的疲劳寿命N存在置信上线和下线,依前文所述置信度的定义,取不失效概率时的寿命,所以疲劳寿命为置信下线。
1)根据正态分布求得期望和方差(如表5),代入式(6)可得不同置信度下的疲劳寿命如图5所示。

表5 不同应变下μ和σ2的值

图5 疲劳寿命 置信度关系曲线(正态分布法)
2)利用对数正态分布计算公式得出的疲劳寿命
对数正态分布是随机变量的对数服从正态分布,所以试验将所得原始数据取对数后进行处理,求得期望和方差(如表6),代入式(6)可得不同置信度下的试样寿命如图6所示。

表6 不同应变下μ和σ2的值

图6 疲劳寿命 置信度关系曲线(对数正态法)
3.3 t分布
由于在实际工作中,往往σ是未知的,这时用t分布来统计计算。
t分布的密度函数如下:
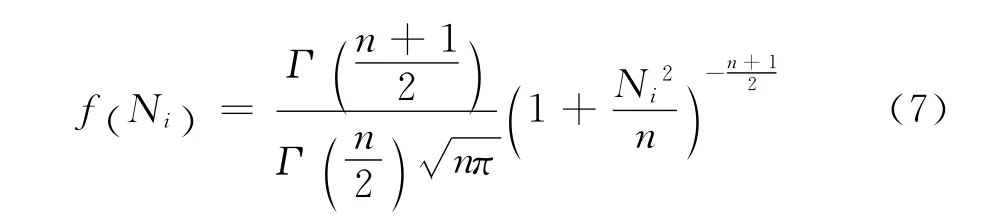
则分布函数为:
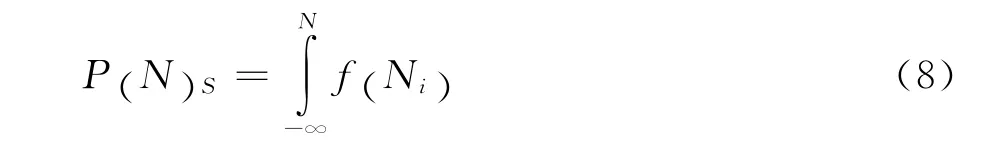
(7)中:n为自由度
假设试验的疲劳数据为t分布,由于试验的样本为6个,所以自由度为5,用软件算出分布的双侧分位数,标准差、抽样平均误差及允许误差(见表7),与正态分布相似取置信下线,则可得到不同置信度下的试样寿命如图7所示:

表7 不同应变下各参数的值
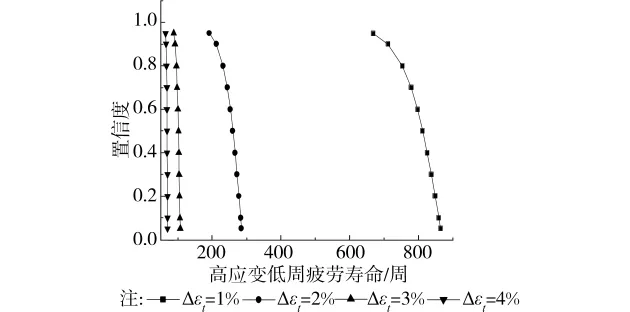
图7 疲劳寿命 置信度关系曲线(t分布法)
3.4 统计结果及分析
不同统计方法得出的置信度为95%下的疲劳寿命N95见表8。
大量的疲劳试验结果表明,材料的塑性应变与疲劳寿命(S N)曲线在双对数坐标中具有大致相同的形式,钢材的双对数S N曲线在某一区间内接近于直线[14-16],由于试验为高应变,且应变取对数,所以弹性应变部分忽略不计,因此本文对应变和统计的疲劳寿命分别取对数后线性拟合。由于单独用QST钢筋不能很好的对比分析,所以本文对超细晶钢筋FG和微合金化钢筋V Fe的低周疲劳寿命也分别做了统计处理。各个拟合曲线的相关系数如表9所示,从中可知,t分布的相关系数R2最大,拟合结果相对最好,正态分布的结果相对最差。

表8 不同统计方法的疲劳寿命N95
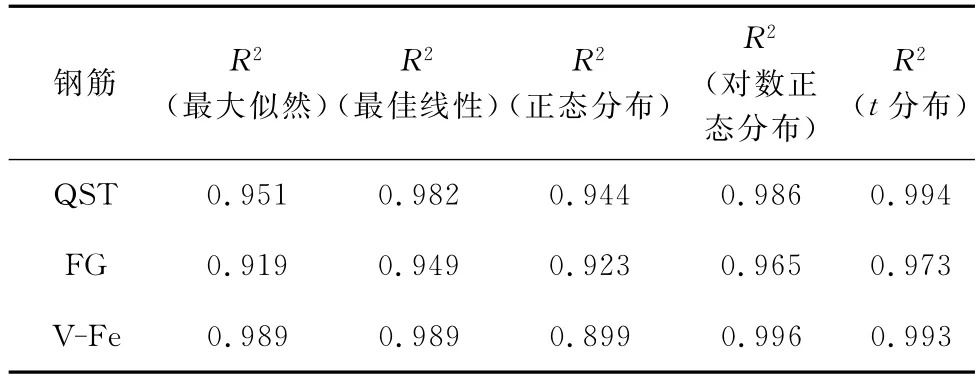
表9 线性拟合的相关系数R2
4 结 论
利用威布尔最大似然、威布尔最佳线性估计、正态分布、对数正态分布和t分布方法,对HRB400抗震钢筋疲劳寿命的原始试验数据进行了处理,可知威布尔最大似然方法和正态分布方法算出的疲劳寿命较为接近,在所有统计方法中威布尔最大似然方法得出的疲劳寿命均较小,因此最为安全,而从最终的应变—疲劳寿命的双对数线性拟合可知t分布求得疲劳寿命最为准确、可靠,正态分布求得疲劳寿命最不准确。所以对钢筋的安全性能要求较高时,用威布尔最大似然方法估算疲劳寿命较好,欲准确得知钢筋的疲劳寿命用t分布方法计算为宜。
[1]郭湛,完卫国,孙维,等.功能性建筑用钢筋的研究现状及发展趋势[J].安徽冶金科技职业学院学报,2010,20(1):3-6.GUO Zhan,WAN Weiguo,SUN Wei,et al.Status and trend of functional steel bar used in constructure[J].Journal of Anhui Vocatonal College of Metallurgy and Technology,2010,20(1):3-6.
[2]黄伟,张丽,王平,等.建筑用钢筋的应用发展研究 [J].建筑技术,2010,41(3):242-245.HUANG Wei,ZHANG Li,WANG Ping,et al.Research on application and development of steel bars used in constructure [J].Architecture Technology 2010,41(3):242-245.
[3]Sheng G M,Gong S H.Investigation of low cycle fatigue behaviors of building [J].Natural Disasters,1997,10(1):51-55.
[4]于孟山,盛光敏,詹苏宇.抗震钢筋研究现状[J].材料导报,2010,24(15):454-458.YU Mengshan,SHENG Guangmin,ZHAN Suyu.Overview of researches on anti-seismic reinforcing bars[J].Materials Review,2010,24(15):454-458.
[5]何才.疲劳试验数据处理及P S N曲线的作用[J].汽车工艺与材料,2007,(4).HE Cai,Fatigue test dada treatment and PS N curve function[J].Automobile Technology & Material,2007,(4).
[6]Zhang X C,Xuan F Z.Stress-dependent fatigue mechanisms of CrC-NiCr coatings in rolling contact[J].Fatigue & Fracture of Engineering Materials &Structures,2011,34(6):438-447.
[7]王旭亮,聂宏.基于灰色系统GM(1,1)模型的疲劳寿命预测方法[J].南京航空航天大学学报,2008,40(6):845-848.WANG Xuliang,NIE Hong.Prediction method for fatigue life based on grey model GM(1,1)[J].Journal of Nanjing University of Aeronautics & Astronautics,2008,40(6):845-848.
[8]Jonathan F,Luiz C W,Ken M.Low cycle fatigue simulation and fatigue life prediction of multilayer coated surfaces[J].Wear,2010,269(9):639-646.
[9]Apostolopoulos C A.Mechanical behavior of corroded reinforcing steel bars S500stempcore under low cycle fatigue[J].Construcion Building Mater,2007,21:1447-1456.
[10]Walter S,Giovanni B,Barbara M,et al.Dual-phase steel re-bars for high-ductile r.c.structures,Part 2:Rotational capacity of beams [J].Engineering Structures,2007,29(12):3333-3341.
[11]杨才福.高强度建筑钢筋的最新技术进展[J].钢铁,2010,45(11):1-11.YANG Caifu.Recent developments of high strength rebars for building[J].Iron and St eel,2010,45(11):1-11.
[12]Sivapragash M,Lakshminarayanan P R,Karthikeyan R,et al.Hanumantha.Fatigue life prediction of ZE41Amagnesium alloy using weibull distribution[J].Materials & Design,2008,29(8):1549-1553.
[13]Raif S,Irfan A.Statistical analysis of bending fatigue life data using Weibull distribution in glass-fiber reinforced polyester composites [J].Materials &Design,2008,29(6):1170-1181.
[14]Chandran K S R,Chang P,Cashman G T.Competing failure modes and complex SN curves in fatigue of structural materials [J].International Journal of Fatigue,2010,32(3):482-491.
[15]Hanaki S,Yamashita M,Uchida H,et al.On stochastic evaluation of SN data based on fatigue strength distribution [J].International Journal of Fatigue,2010,32(3):605-609.
[16]Zhao Y X,Yang B,Feng M F,et al.Probabilistic fatigue S-N curves including the super-long life regime of a railway axle steel[J].International Journal of Fatigue,2009,31(10):1550-1558.

