用细观单元等效化方法模拟混凝土细观破坏
杜修力,金 浏
(北京工业大学 城市与工程安全减灾教育部重点实验室,北京100124)
混凝土是典型的非均匀材料,其复杂的破坏机理及宏观力学特性是研究者一直关注的问题。混凝土类非均质材料的破坏过程实际上就是微裂纹萌生、扩展、贯通,直到最后宏观裂纹产生导致混凝土失稳破裂的过程。
对于非均匀混凝土材料问题,学术界进行了长期的探索,在近30年来已取得了很大的进展,提出了很多研究混凝土损伤断裂过程的细观力学模型[1]。Wang等[2-3]提出了随机骨料模型,采用 非线性有限元技术,研究了混凝土试件的损伤断裂全过程;Schlangen等[4]采用简单格构模型研究了混凝土等脆性材料的典型破坏机理;Mohamed等[5]提出了混凝土破坏机制研究的微观结构模型,考虑混凝土细观组分力学性质的随机性,引入断裂能概念,采用弥散裂纹模型描述单元受拉行为,对混凝土试件的破坏机理进行了研究;唐春安等[6]借助统计学及数值模拟方法,建立了混凝土损伤断裂研究的随机力学特性模型;Lopez等[7]采用“零厚度”界面单元法对混凝土试件在单轴拉伸下的断裂破坏过程进行模拟,获得的宏观力学特性与试验结果吻合良好;杜修力等[8]提出了高计算效率的细观单元等效化模型,对混凝土材料的力学性能进行研究,数值结果与试验结果吻合良好。这些研究工作,大多采用连续介质力学与不可逆热力学理论,导出相应的连续损伤力学本构方程和演化方程,进而研究混凝土断裂破坏机理及宏观力学性能。
笔者拟将细观单元等效化模型在连续介质力学领域的应用延伸或扩展到非连续介质力学范畴,从而更便于宏观地认识混凝土材料内部裂纹的扩展演化过程。基于该理念,笔者首先简要阐述细观单元等效化模型及扩展有限元法的基本原理;其次,对细观单元的等效力学性能作理论推导并进行数值验证;最后采用扩展有限元法来研究混凝土材料的细观断裂破坏过程及其宏观力学性能。
1 基本思想及原理
1.1 细观单元等效化模型简介
细观单元等效化模型,从描述混凝土材料的细观尺度入手,认为混凝土材料的宏观非线性及尺度效应根源于其内部细观组成的非均质性,细观组成的非均匀性导致宏观力学行为的非线性。为反映混凝土材料非均匀性的本质特征,文献[9]基于概率统计学理论,提出以细观单元材料力学特性(弹性模量)的变异系数作为材料非均匀性量度的指标,并给出了混凝土材料的特征单元尺度。采用特征单元尺度对混凝土细观随机骨料模型划分网格后,得到的等效力学模型能准确地表征混凝土材料的非均匀特性。简单的讲,采用“材料特征单元尺度”来剖分有限元试件网格后获得的等效力学系统,足以能够准确获得混凝土材料的宏观力学性能。
如图1所示的混凝土材料细观单元等效化模型,首先在混凝土细观随机骨料模型的基础上,采用“材料特征单元尺度”来剖分有限元网格并投影到已建立的随机骨料模型上,得到的各细观单元等效力学特性采用复合材料力学等效化方法来确定。非均质混凝土材料力学体系最终等效成单元内均匀且各向同性、单元间性质各异的非线性力学模型。细观单元等效化模型,本质上是以材料分布的不均匀性来体现整个试件的宏观非线性。

图1 细观单元等效化模型
1.2 扩展有限元(X-FEM)法
Belytschko等[10-12]基于单位分解(PUM)[13-14]概念,利用有限元法的形函数作为一组单位分解函数,并将非连续函数引入定义在覆盖(节点影响域)上的位移模式中,即

式中:I为离散域中所有节点的集合,J为影响域被非连续界面穿过的节点的集合,Ni(x)和Nj(x)分别为节点i、j影响域上的形函数,函数 H(x)为Heaviside函数,ui和uj均为常规的连续位移模式的系数,dj为非连续位移模式的系数。引入了非连续位移模式,使得扩展有限元在对不连续位移场描述时不再依赖单元边界,也不需要对网格进行重剖分,可以用来求解函数不连续(如裂纹)[15]、导数不连续(如夹杂、移动相边界)[16]、函数切向分量不连续(如剪切带、流固耦合)和概貌加强等问题。文献[15]证明了扩展有限元在非均匀混凝土材料细观破坏过程及宏观力学性能研究中的可行性,但其计算效率低下问题也将限制其在三维力学计算模型中的更多应用。
2 细观单元等效力学性质
2.1 细观单元等效力学性能
采用细观单元等效化思想来分析混凝土材料细观断裂破坏及研究宏观力学特性时,需要对细观单元的力学性质进行等效化分析。在细观尺度上,可以认为混凝土是由骨料、砂浆及界面组成的三相复合材料。采用特征单元尺度剖分混凝土随机骨料模型后获得的细观单元内骨料、砂浆及界面相组成的某空间分布,如图2(a)所示,将其进行力学等效化后形成的均匀各向同性的单元如图2(b)所示。与图2(a)宏观力学特性相等效的图2(b)的力学性质如何?下面,理论推导分析细观单元的等效体力学性质。
图2(a)中混凝土细观各相材料(骨料、砂浆及界面)采用如图3(a)、(b)、(c)所示的本构关系,即:细观组分在达到峰值应力前,应力 应变关系是线弹性的;达到强度后,采用线性应力 裂缝宽度关系来表征混凝土材料的软化行为。ft为极限抗拉强度;Gf为断裂能;W为张开位移;WS为极限张开位移。

图2 混凝土细观单元及其等效体

图3 混凝土细观组分本构关系
假定等效体图2(b)的本构行为与各组分本构关系形式类似,如图3(d)所示。那么在对混凝土细观单元力学特性进行等效化时,需要获得的力学参数有等效弹性模量Eeq,等效泊松比υeq,等效断裂强度feqt及单元等效断裂能Geqf。对这些参数的等效化分析,采用如下处理。
1)等效体弹性模量Eeq及υeq
采用Vogit并联模型[17]对弹模及泊松比进行等效化处理,得:
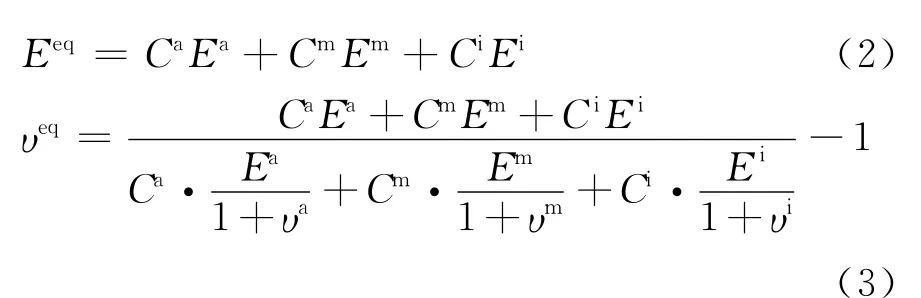
式中:上标“eq”表示细观等效体,上标“a”、“m”及“i”分别表示骨料、砂浆及界面,C为体积分数。
2)等效断裂强度feqt
当细观等效体达到其断裂强度feqt时,认为在等效体内产生的内能(应变能)是其细观组成(骨料、砂浆及界面)的总和,等效体内储存的应变能Ωeq为:

即:
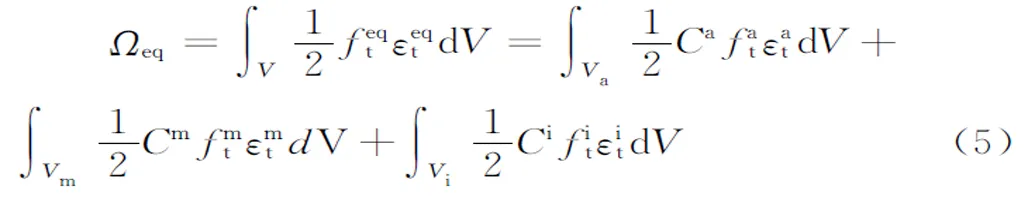
对于细观单元等效体,知:

式中Ωa、Ωm及Ωi分别为骨料、砂浆及界面分别达到其抗拉强度时所存储的应变能。
将式(6)代入式(5),得:
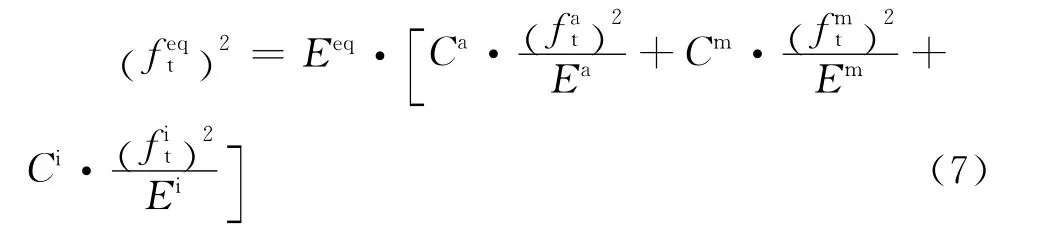
3)断裂能Geqf
这里假定细观等效体的断裂能Geqf与其细观组分的断裂能关系如下:

2.2 细观单元等效力学特性验证
为验证2.1节所提出的等效化方法的准确性,对细观单元的等效力学特性进行验证。
选择5组细观单元网格中骨料及砂浆的随机分布情况,如图4(a)~(e)所示,将其作为不同的随机样本来进行数值验证,5组样本中骨料所占据的体积分数均取为30%。采用扩展有限元方法对其进行数值分析(以单轴拉伸行为为例),5组样本得到了5组不同的宏观应力-应变关系曲线,如图5所示。获得的宏观应力-应变关系曲线与笔者力学等效化理论方法(图5中“粗线”所示)吻合非常好,从而验证了笔者等效化力学方法的准确性。笔者进行了大量的随机样本数值试验,均发现得到的结果与2.1节提出的等效力学特性相吻合,由于篇幅所限,这里不做多述。
3 算例分析
3.1 二维混凝土单轴拉伸破坏过程

图4 典型样本及等效体
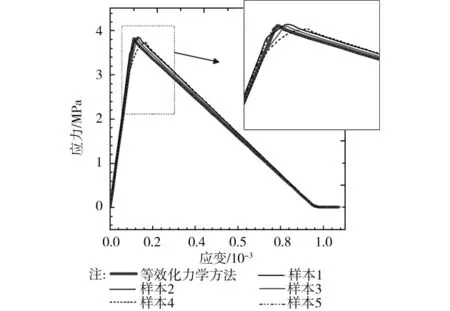
图5 等效化方法与数值结果对比
图6(a)为混凝土试件的细观随机骨料模型,试件尺寸为150mm×150mm,其细观组分采用图3所示的本构模型,其力学参数如表1所示。图6(b)为采用混凝土材料特征单元尺度对图6(a)进行网格划分后,采用前面所述方法对细观单元进行等效化而获得的细观单元等效化模型,不同的单元拥有不用的颜色,表示不同的力学特性(如弹模、泊松比、强度及断裂能等)。混凝土试件底面竖向固定约束,侧面为自由面,顶面为载荷输入面,这里采用位移加载控制,如图6(b)所示。将最大主应力准则作为混凝土细观单元的断裂准则。
基于细观单元等效化模型思想理念,采用扩展有限元数值方法,对单轴拉伸行为下混凝土随机骨料模型的两组样本试件的断裂破坏过程进行数值研究,得到2组样本及其对应细观单元等效化分析方法的裂纹扩展路径,并获得其对应的混凝土宏观应力 应变关系曲线,如图7所示。
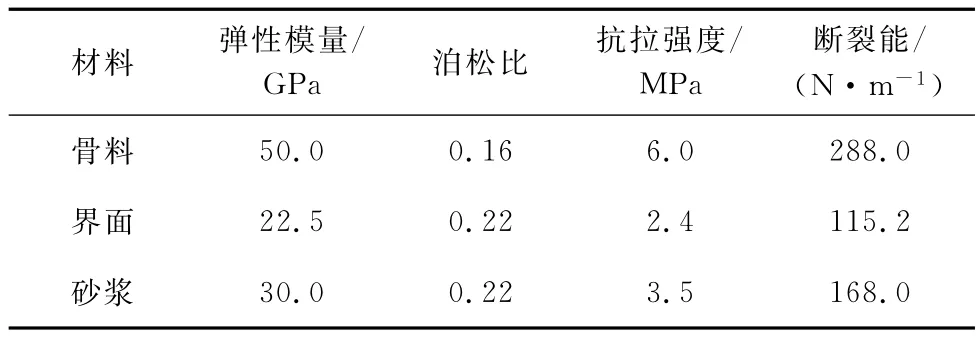
表1 混凝土各组分力学性质
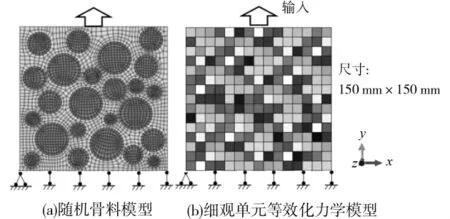
图6 混凝土细观有限元模型

图7 混凝土试件2组样本裂纹路径及宏观p ε关系
从图7中可以看出:1)采用笔者提出的细观单元等效化模型,能很好地模拟混凝土试件的裂纹扩展过程及裂纹模式,与采用细观随机骨料模型所得到的最终裂纹路径基本相同;2)相对于细观随机骨料模型(2个样本的单元数分别为3 826和3 625)而言,采用细观单元等效化模型,在使用很少的网格单元下(该算例模型为225个单元)便可以较为准确的获得混凝土材料的宏观力学性能,获得的混凝土材料的宏观弹模及强度等均与随机骨料模型结果吻合良好,仅下降段曲线略有区别。
3.2 三维混凝土单轴拉伸破坏过程
细观单元等效化模型的高效性使得三维混凝土细观裂纹扩展过程及宏观力学性能的研究成为可能。采用Monte Carlo法建立如图8(a)所示的二级配混凝土三维随机骨料模型,并得到与之力学性能相对应的三维细观单元等效化模型,图8(b)所示,模型尺寸为150mm×150mm×150mm。细观单元等效化模型中,各细观单元的尺寸为10mm×10mm×10mm,共3 375个单元,各细观单元采用图3(d)所示的本构关系来表征其力学行为。
对混凝土2组样本试件进行分析研究,获得其宏观应力 应变关系曲线如图9所示,分别得到混凝土单轴抗拉强度为3.45、3.38MPa。

图8 细观混凝土有限元计算模型

图9 混凝土材料单轴拉伸宏观p ε关系曲线
图10 为混凝土一组随机样本试件在单轴拉伸条件下的最大主应力变化云图及试件的裂纹扩展演化过程。材料的不均匀分布导致混凝土内部应力分布的不均匀,最终导致混凝土材料的非线性。裂纹扩展状态A、B、C、D、E、F下,混凝土宏观力学性能对应于图9中应力 应变关系曲线的几个状态点。
从图10中可以看出,在外荷载作用下,混凝土试件首先在内部薄弱的区域产生应力集中,进而达到细观单元的抗拉强度而产生断裂;随着外载增大,裂纹面不断扩展演化,较大的区域产生宏观裂纹面,当其达到C状态时,混凝土宏观平均应力达到最大值,继而试件整体刚度突降,裂纹面不断扩展演化,经历D、E状态而直至最终的完全断裂,即F状态,混凝土试件应力全部释放。混凝土试件内应变能、内能及断裂耗散能与宏观应变的关系曲线如图11所示。混凝土应变能随外载荷的增大呈现先增大后减小直至为零的趋势;体系的断裂耗散能在试件达到一定的宏观应变时突然产生,并逐渐增大直至达到一恒定值。

图10 裂纹带扩展演化过程
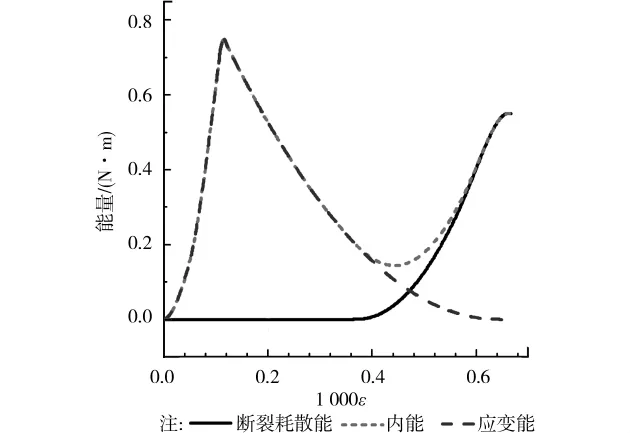
图11 混凝土细观结构体系能量与应变ε的关系
图12 为2组不同随机样本(骨料空间分布形式不同)的细观单元等效化模型,在单轴拉伸条件下的最终裂纹模式图。2个裂纹带的不同,说明了骨料空间分布的不同,影响混凝土材料的裂纹扩展路径,这从图9的宏观应力 应变关系曲线下降段的区别也可以得到体现。
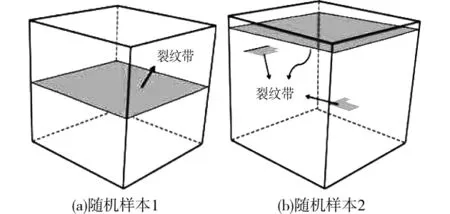
图12 两不同样本最终裂纹带
这些研究结果表明,采用笔者提出的细观单元等效化方法来研究混凝土细观断裂破坏过程,在较低计算量的情况下便可以获得较为准确的计算结果,这解决了其它细观力学模型(如随机骨料模型,随机力学特性模型等)计算效率低下的“瓶颈”问题,使得从细观层次上研究更为复杂的大体积混凝土材料及混凝土构件的破坏机理及力学性能成为可能。
4 结语
从非连续介质力学角度出发,在细观单元等效化力学模型的基础上,采用扩展有限元方法来研究混凝土材料的细观裂纹扩展过程。推导了细观单元的等效力学特性,并进行了数值验证;最后对单轴拉伸条件下湿筛混凝土的二维及三维试件进行了数值分析,研究其裂纹扩展过程及宏观力学性能,获得与细观随机骨料模型相吻合的结果,验证了细观单元等效化力学模型的准确性和高效性。实现了细观单元等效化力学方法在非连续介质力学领域的应用,从而更清晰地模拟了混凝土在外荷载作用下的断裂破坏过程。
[1]杜修力,金浏.混凝土静态力学性能的细观力学方法述评[J].力学进展,2011,41(4):411-426.DU Xiuli,JIN Liu.A review on meso-mechanical method for studying the static-mechanical properties of concrete[J].Advances in Mechanics,2011,41(4):411-426.
[2]Wang Z M,Kwan A K H,Chan H C.Mesoscopic study of concrete I:generation of random aggregate structure and finite element mesh[J].Computers and Structures,1999,70(5):533-544.
[3]Kwan A K H,Wang Z M,Chan H C.Mesoscopic study of concrete II:nonlinear finite element analysis[J].Computers and Structures,1999,70(5):545-556.
[4]Schlangen E,Garboczi E J.Fracture simulations of concrete using lattice model computational aspects[J].Engineering Fracture Mechanics,1997,57(2/3):319-332.
[5]Mohamed A R,Hansen W.Micromechanical modeling of crack-aggregate interaction in concrete materials[J].Cement and Concrete Composites,1999,21(5/6):349-359.
[6]唐春安,朱万成.混凝土损伤与断裂 数值试验[M].北京:科学出版社,2003.
[7]Lopez C M,Carlo I,Aguado A.Meso-structural study of concrete fracture using interface elements I:numerical model and tensile behavior[J].Materials and Structures,2008,41(3):583-599.
[8]杜修力,金浏.混凝土材料宏观力学特性分析的细观单元等效化模型[J].计算力学学报,2012,29(5):654-661.DU Xiuli,JIN Liu.Meso-element equivalent model for macro-scopic mechanical properties analysis of concrete materials [J].Chinese Journal of Computational Mechanics,2012,29(5):654-661.
[9]杜修力,金浏.混凝土材料细观单元弹模非均匀统计特性研究[J].工程力学,2012,29(10):106-115.DU Xiuli,JIN Liu.Research on the heterogeneous clouds[J].Computer Methods in Applied Mechanics and Engineering,1996,139:237-262.
[15]黄景琦,金浏,杜修力.界面特性及骨料分布对混凝土破坏模式的影响[J].土木建筑与环境工程,2011,33(S2):38-41.HUANG Jingqi,JIN Liu,DU Xiuli.The impact of interface characteristic and aggregate distribution on failure modes of concrete [J].Journal of Civil,Architecture and Environmental Engineering,2011,33(S2):38-41.
[16]应宗权,杜成斌,王友元.颗粒增强复合材料的扩展有限元模拟方法[J].水利学报,2011,42(2):198-203.YING Zongquan,DU Chengbin,WANG Youyuan.Numerical simulation of particle reinforced composite using extended finite element method[J].Journal of Hydraulic Engineering,2011,42(2):198-203.
[17]Voigt W.Uber die Beziehung zwischen den beiden Elastizitätskonstanten isotroper Körper[J].Wied Ann,1889,274(12):573-587.statistical properties of elastic modulus of concrete meso-scale element[J].Engineering Mechanics,2012,29(10):106-115.
[10]Belytschko T,Black T.Elastic crack growth in finite element with minimal remeshing [J].International Journal for Numerical Methods in Engineering,1999,45(5):610-620.
[11]Moes N,Dolbow J,Belytschko T.A finite element method for crack growth without remeshing [J].International Journal for Numerical Methods in Engineering,1999,46(1):131-150.
[12]Daux C,Dolbow J,Sukumar N,et al.Arbitrary branched and intersecting cracks with the extended finite element method [J].International Journal for Numerical Methods in Engineering,2000,48(12):1741-1760.
[13]Melenk J M,Babuka I.The partition of unity finite element method:basic theory and applications [J].Computer Methods in Applied Mechanics and Engineering,1996,139:289-314.
[14]Duarte C A,Oden J T.An H-P adaptive method using

