地震作用下钢框架混凝土核心筒组合结构体系的抗震性能

巩玉发，尹兆岩，王琦琳

（辽宁工程技术大学 辽宁省阜新，123000）

钢框架 混凝土组合结构是外框架采用钢结构，内筒采用混凝土剪力墙结构，形成钢框架－混凝土内筒体系。这种结构形式将混凝土核心筒和与之铰（刚）接的钢结构框架联合使用，由具有较大侧向刚度的混凝土核心筒或剪力墙承受大部分水平荷载，而具有较高材料强度的钢结构主要承受竖向荷载，两种材料的巧妙组合能满足建筑使用功能上的灵活性要求，避免了单一结构体系带来的弊端［1］。在结构受力方面，可减轻结构自重，提高竖向承载力和抗风抗震能力，增强了结构的延性，使结构高度不断突破钢筋混凝土结构的极限，同时可加快施工速度，降低结构成本，提高建筑面积使用率［2］。与钢结构相比，可以减小用钢量，增大刚度，增加稳定性和整体性，提高结构的抗火性和耐久性等［3］。

本文设计了一个钢框架 混凝土核心筒组合结构体系模型，对其进行地震作用下的地震响应分析和稳定性分析。为了更好地认识地震作用下钢框架 混凝土核心筒组合结构体系的抗震性能，本文还设计了一个与该结构相近的纯钢框架结构体系模型，将两个模型进行对比分析。

1 结构模型

1.1 模型的平面图及截面尺寸汇总

本文采用的模型A为一栋25层办公楼（定义为模型A），总高100m，层高4m，Ⅱ类场地，抗震设防烈度为8度，抗震等级为Ⅰ级，设计使用年限为100年。平面尺寸为48m×28m，柱距为8m，边跨为8m，中跨为10m，高宽比为3.85。钢材料选Q235钢，弹性模量为2.06×1011N／m2，泊松比为0.3，密度为7 850kg／m3。核心筒的混凝土强度等级为C40，弹性模量为3.25×1010N／m2，泊松比为0.2，密度为2 500kg／m3。楼板和墙体的混凝土强度等级为C30，弹性模量为3.00×1010N／m2，泊松比为0.2，密度为2 500kg／m3。

模型B的平面布置和结构尺寸与A完全相同，只是该结构为纯钢框架结构，其中心内部由钢框架梁代替了混凝土核心筒体。

2个模型的平面图如图1所示，模型A的平面图如图1（a）所示，模型B的平面图如图1（b）所示，模型A和模型B的截面尺寸如表1。

表1 模型的构件截面尺寸 mm

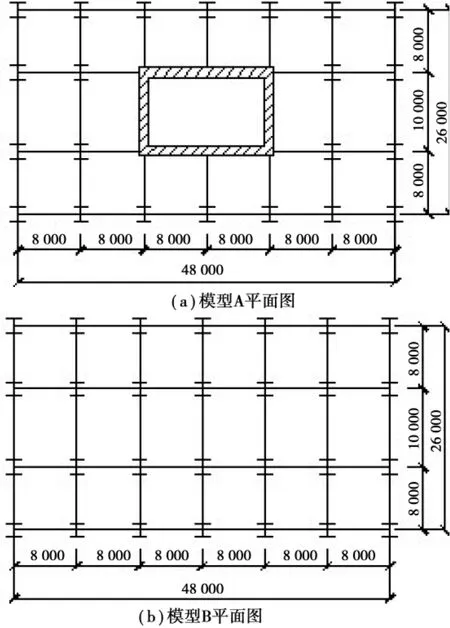
图1

1.2 工程数值模拟分析

以ANSYS有限元程序做为通用平台，通过选择合理的单元类型、设置单元实常数、定义材料属性，建立数值模拟分析模型。

模型A：

1）单元类型：梁单元类型采用“BEAM188”三维有限应变梁单元，筒体楼板及外墙单元类型采用“SHELL181”四节点三维壳单元。

2）单元实常数：定义框架柱截面实常数为1，尺寸为0.30 m×0.50m；外环梁截面实常数为2，尺寸为0.15m×0.30 m；内框架梁截面实常数为3，尺寸为0.10m×0.30m；定义楼板及墙体实常数为2，厚度为0.20m；筒体实常数为3，厚度为0.40m。

3）材料属性：钢材料选Q235钢，弹性模量为2.06N／m2，泊松比为0.3，密度为7 850kg／m3。核心筒的混凝土强度等级为C40，弹性模量为3.25×1010N／m2，泊松比为0.2，密度为2 500kg／m3。楼板和墙体的混凝土强度等级为C30，弹性模量为3.00×1010N／m2，泊松比为0.2，密度为2 500kg／m3。

有限元模型如图2。

图2 模型A有限元模型

模型B：

1）单元类型：梁单元类型采用“BEAM188”三维有限应变梁单元，楼板及外墙单元类型采用“SHELL181”四节点三维壳单元。

2）单元实常数：定义框架柱截面实常数为1，尺寸为0.30 m×0.50m；外环梁截面实常数为2，尺寸为0.15m×0.30 m；内框架梁截面实常数为3，尺寸为0.10m×0.30m；定义楼板及墙体实常数为2，厚度为0.20m。

3）材料属性：钢材料选Q235钢，弹性模量为2.06×1011N／m2，泊松比为0.3，密度为7 850kg／m3。楼板和墙体的混凝土强度等级为C30，弹性模量为3.00×1010N／m2，泊松比为0.2，密度为2 500kg／m3。

有限元模型如图3。

图3 模型B有限元模型

2 结构的模态分析

2.1 结构模态分析的自振周期和自振频率

结构的地震反应不仅取决于地震动力特性，结构自身固有特性也存在一定影响。结构自身固有特性是结构在无阻尼情况下得到的结构自由振动频率和相应的振型。结构在地震荷载作用下，各构件的最大内力、位移和变形都与结构自身的固有振动频率和相应的振型相关，因此各项动力分析的前提和基础就是求出结构的自振频率和振型。模态分析一般用于确定结构的振动特性，即确定结构的固有频率和振型，也是谐响应分析、瞬态分析及谱分析等其它动力学分析的起点［4］。因此首先要进行模态分析。

表2 模型A前6阶自振周期和自振频率

表3 模型B前6阶自振周期和自振频率

通过ANSYS软件进行模态分析选取前6阶自振周期和自振频率，使我们了解了该模型结构振动的基本振型对应的频率，这些基本自振频率可以给我们一个准则，即在实际中可以避开这些基本自振频率，以防止共振。

自振周期和自振频率也可以用来衡量结构稳定性的好坏，结构的自振周期越小，自振频率越大表示结构的稳定性就越好。本文通过模态分析所得出的表2和表3数据，对比模型A和模型B的自振周期和自振频率可知，模型A的自振周期小于模型B的自振周期，模型A的自振频率大于模型B的自振频率，则说明模型A结构的稳定性比模型B结构的稳定性好。

2.2 结构模态分析的振型分析

进行结构的模态分析，还需要拟定几个振型来确定结构的变形趋势，而结构的前几阶振型起主要作用，因此在计算式主要提取前几阶的振型来分析。模型A前3阶的振型如图4。

图4 模型A前三阶振型图

从振型图4可以看出模型A的第1振型为Y方向整体平动，对应频率为1.222 8Hz，周期为0.818 0s对应的最大位移为0.293mm；第二振型为X方向整体平动，对应频率为1.790 6Hz，周期为0.558 5s，对应的最大位移为0.282mm。由此得出第1主振型Y方向的最大位移大于第2主振型X方向的最大位移，则Y方向为短轴方向，X方向为长轴方向，沿长轴方向布置的梁柱多于沿短轴方向布置的梁柱，使Y方向的刚度较X方向的小，因此结构的振动控制方向为Y方向。第3振型为绕Z轴方向的扭转振型，对应频率为2.734 2Hz，周期为0.365 7s，符合《高层建筑混凝土结构技术规程》［5］中前两阶振型不能为以扭转振型为主的规定。此外结构以平动为主的第1自振周期T1＝0.818 0s，以扭转为主的第1自振周期T3＝0.365 7s，其比值T3／T1＝0.45，低于《高层建筑混凝土结构技术规程》中规定的值0.85，说明该结构设计符合规范要求。

3 选取地震波进行地震响应计算分析

目前有关地震波的选择主要有下列2种方法，一是直接利用典型的强震记，二是采用人工地震波，按照拟建场地的地基和建筑物状况，按概率方法人工地产生一种随机的地震波。本文中考虑的强震记录，根据场地条件和烈度要求，选择了适合Ⅱ类场地的EL－Centro波。输入的地震波对建筑物的作用方向为沿X坐标轴方向、Y坐标轴方向。定义楼层1层、10层、25层节点在X、Y方向的位移共6个变量。地震波的持续时间取5s，时间间隔为0.1s。

由模型A的3层节点在X、Y方向的瞬态位移响应曲线看出，钢框架 混凝土核心筒组合结构在其下部楼层，核心筒体的位移较小，它拉着框架按照弯曲型变形，上部楼层则相反，核心筒体位移越来越大，有外扩的趋势，而框架则有内收的趋势，框架拉核心筒按照剪切型曲线变形。

图5 3层节点瞬态位移响应曲线（X方向）

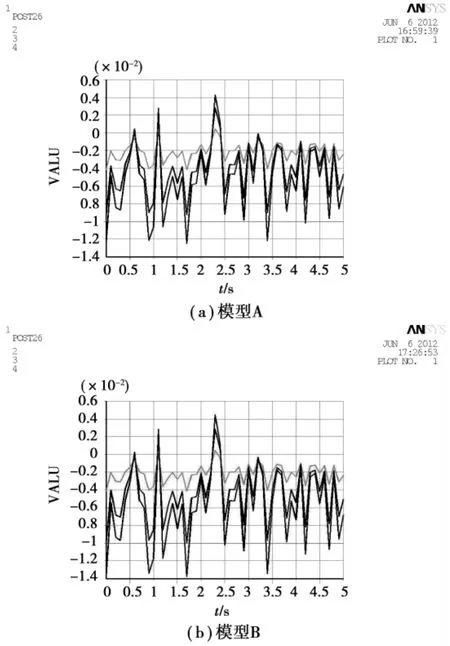
图6 3层节点瞬态位移响应曲线（Y方向）

再由图5和图6可以看出，在同一地震波作用下，模型A没有模型B的总位移曲线变化剧烈，模型B的偏移位移大于模型A的偏移位移，说明模型A结构更加安全和完善。

4 结构的稳定性分析

稳定分析又叫屈曲分析，所谓稳定性在工程结构上指结构或构件受力后保持原有稳定平衡状态的能力。临界荷载Fcr是指使压杆直线形式的平衡，开始由稳定转变为不稳定的轴向压力值。而临界荷载系数（荷载安全系数）均是对应于某种工况或荷载组合的。本文对2种模型的所有楼板分别施加每单位面积均为1kN／m2的均布荷载，如图7。

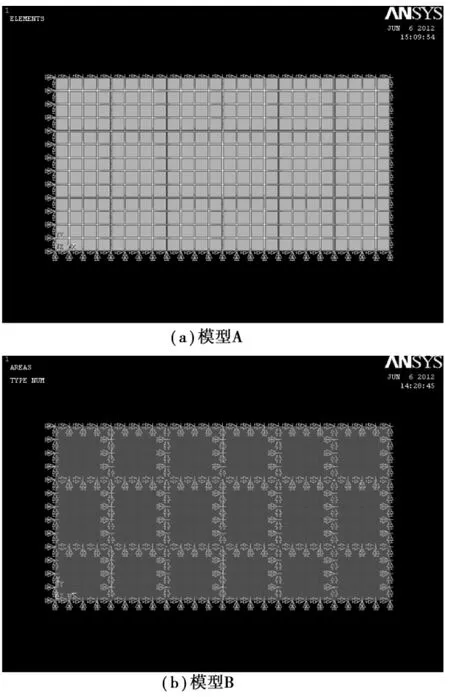
图7 楼板施加均布荷载计算简图

通过ANSYS软件对2种模型进行计算得出2种模型的临界荷载系数nst分别为84.909，78.985。再由理论公式Fcr＝F·nst得出临界荷载值（其中F包括所有结构的重力与所有楼板均布力之和）分别为：

模型 A：Fcr＝3.28×107kN

模型B：Fcr＝3.12×107kN

由上式可知模型A的临界荷载值大于模型B的临界荷载值，则模型A的结构稳定性大于模型B的结构稳定性，这就说明模型B结构体系比模型A结构体系容易发生破坏。而由于模型A的结构体系由于临界荷载较大，不但减小了位移的变化，而且使框架柱抵抗倾覆力矩的性能得以提高，进而说明模型A结构体系的抗震性能比模型B结构体系的抗震性能更加优越。

5 结 论

本文通过对两个模型进行模态分析并输入适合Ⅱ类场地的EL Centro波，对钢框架－混凝土组合结构体系（模型A）和纯钢框架结构体系（模型B）进行了地震作用下的抗震性能分析和结构稳定性分析，分析结果表明：

1）模态分析计算出的自振频率可以给我们一个准则，即在实际中可以避开这些基本自振频率，以防止共振。

2）由于第1主振型Y方向的最大位移大于第2主振型X方向的最大位移，则Y轴方向为短轴方向，X轴方向为长轴方向，即结构的振动控制方向为Y方向。

3）钢框架 混凝土核心筒组合结构在其下部楼层，核心筒体的位移较小，它拉着框架按照弯曲型变形，上部楼层则相反，核心筒体位移越来越大，有外扩的趋势，而框架则有内收的趋势，它拉着核心筒按照剪切型曲线变形。

4）纯钢结构体系位移时程曲线变化剧烈，其偏移位移大于钢框架 混凝土核心筒组合结构体系的偏移位移，这说明钢框架 混凝土核心筒组合结构更加安全和完善。

5）钢框架 混凝土核心筒组合结构体系的稳定性好于纯钢结构体系的稳定性，且由于钢框架 混凝土核心筒组合结构体系临界荷载较大，不但减小了位移的变化，而且使框架柱抵抗倾覆力矩的性能得以提高，进而说明钢框架 混凝土核心筒组合结构体系的抗震性能比纯钢结构体系的抗震性能更加优越。

［1］Michael D.Conceptsof composite construction－mutatis mutandis［C］.Composite Construction－Conventional and Innovative，Innsbruck，Austria，1997：19－28.

［2］李勇，孙立杰.高层建筑结构特点、现状及发展趋势［J］.黑龙江科技信息，2010.

［3］徐培福，傅学怡，王翠坤，等.复杂高层建筑结构设计［M］.北京：中国建筑工业出版社，2005：392－399.

［4］王金龙.ANSYS12.0土木工程应用实例解析［M］.北京：机械工业出版社，2010.

［5］JGJ3—2010高层建筑混凝土结构技术规程.北京：中国建筑工业出版社，2011.