快速傅里叶变换的硬件实现

兰海洋，林晓焕

（西安工程大学 电子信息学院，陕西 西安 710048）

0 引言

19世纪20年代，法国工程师傅里叶（Fourier）指出：任意一个周期函数都可以分解为无穷多个不同频率正弦信号的和，这即是傅里叶级数[1]，求解傅里叶系数的过程就是傅里叶变换。傅里叶变换的应用非常广泛，主要的领域有：物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等[2]。快速傅里叶变换（FFT）是离散傅里叶变换（DFT）的一种快速算法。一般采用 ROM 的方法来实现FFT，其速度不能满足实时性的要求[3]，这里采用移位存储器的方法来存储旋转因子，大大地提高了FFT的运算速度。

1 算法原理

设长度为N的有限序列x(n)的DFT为：

设序列x(n)的长度N(N=2M,M为任意整数)按N的奇偶性把x(n)分解为两个N/2点的子序列：

则x(n)的N点DFT为：

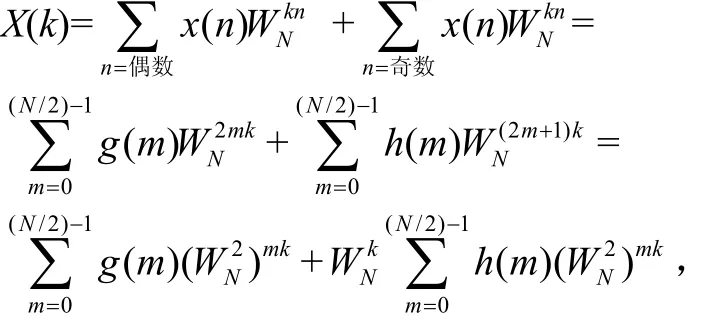
由于

所以

式中，G(k)和H(k)分别为 g(m)和 h(m)的 N/2点 DFT，表达式如下：

由于G(k)和H(k)均以N/2为周期，考虑到对称性，有,X(k)就可表达式为：

这样就将N点的DFT分解为两个N/2点的DFT以及上面两式的运算，使DFT运算量减少，将每个N/2点的DFT分解为两个N/4点的DFT，由于N是2 的正整数次幂，还可以继续分下去，直到分解为2点的DFT为止，这种运算可用图1的流图表示，称为蝶形运算符。当N=8时[5]，整个信号的流图如图2所示。

图1 蝶形运算符

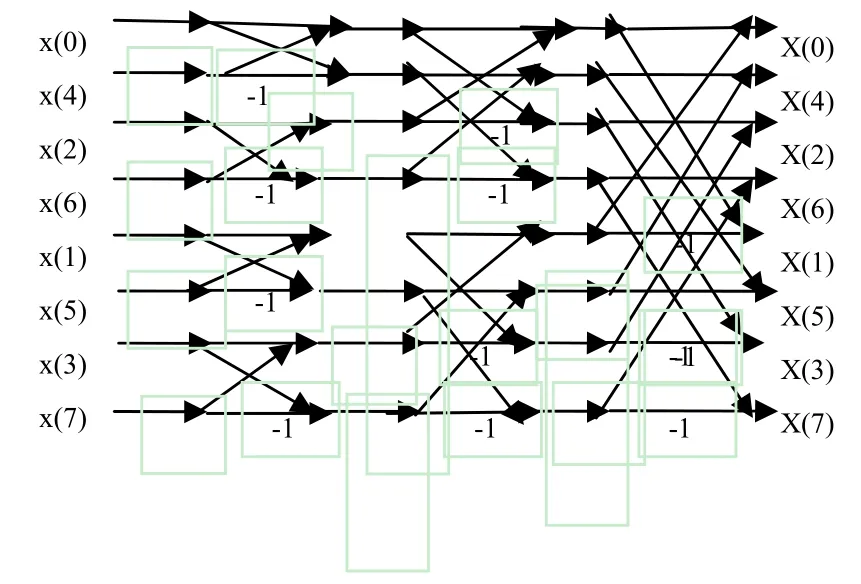
图2 8点FFT蝶形运算示意

2 电路过程原理

2.1 FFT的总体设计

FFT设计主要由以下部分组成：蝶形运算单元，地址产生单元，功能切换单元，存储单元，浮点单元和时序控制元。各模块功能如下：

蝶形运算单元采用DIT方式完成FFT的蝶形运算，双口RAM1和 RAM2作为存储器，从RAM1中读出数据存入RAM2中，或从RAM2中读出数据存入RAM1中。ROM作为预置旋转因子的存储单元，功能切换单元用来完成RAM1与RAM2间数据读写功能的切换；地址产生单元用于产生 RAM 的读、写地址和 ROM 的读地址；浮点单元用于记录蝶算单元输出数据的位信息并完成蝶算单元输入数据的截位；时序控制单元：产生各模块的使能信号、控制信号，使整个流程正常有序的工作。

2.2 蝶形单元的设计

由以上分析可知，蝶形运算单元是FFT算法最核心的的部分。因此要实现FFT算法电路，首先是设计蝶形运算单元，然后利用蝶形模块及其他几个模块的配合实现FFT。

由图1可知，蝶形模块的输出为A+BC和A-BC。这里涉及加法、减法、和乘法的相互运算，即蝶形运算单元的电路主要由加法器、减法器和乘法器构成[5]。

1）N为加法器。多为加法器的构成有两种方式：串行进位和并行进位。串行进位方式是将全加器级联构成多为加法器。并行进位加法设有并行进位产生逻辑，运算速度快；并行进位加法器通常比串行级联加法器占用的资源多。随着位数的增加相同位数的并行加法器与串行加法器的资源占用快速增大。蝶形运算模块中采用并行进位的实现方式[6]。

2）N位乘法器。N位乘法器的运算方法和手工算法一样，是由N位加法器构成的以时序逻辑方式设计的N×N位乘法器方案，其原理是：若被乘数某位为 1，则乘数左移几位，若为 0则不进行运算，然后逐次相加，直至被乘数的最高位[7-8]。

3）N位减法器。其设计方法和原理和加法器相同。

以输入信号为8为二进制数来实现FFT设计，具体说明如何利用Verilog HDL语言完成蝶形运算单元的设计与实现。图3为蝶形运算单元的核心电路图，蝶形运算的实现由乘法器、加法器和减法器和控制输出使能模块相互运算完成的。

图3 蝶形运算单元的核心电路

其中X1_r，X1_im，X2_r，X2_im分别为X1，X2的实部与虚部，c,d分别代表复数的实部与虚部；y1_r,y2_r,y1_im,y2_im分别代表输出y1,y2的实部与虚部，他们分辨对应于A+BC和A-BC的实部与虚部。图4为蝶形运算单元模块。

图4 蝶形运算单元模块

3 实验结果

在XILinxA公司的FPGA上进行验证，目标芯片采用Virtex系列的XCV300，编写软件为ISE 10.1。

Virtex是Xilinx FPGA中的高端产品，内部有丰富的资源，包括RAM，乘法器，IOB，可编程互联线，数字时钟管理器 DCM 和可编程逻辑阵列CLB，这一系列产品不断的升级和更新，性能也越来越卓越。 FFT的仿真图如图5所示。由波形图5中可以看出，当Start为低电平时，FFT开始运算，给输入端顺序送入8个数据，计算结束后，数据从输出端顺序输出。大大提高了运算速度。

图5 FFT运算仿真波形

4 结语

文中采用Verilog语言实现FFT算法，利用ISE进行仿真，在分析快速傅里叶变换（FFT）算法的基础上[9-10]，采用移位存储器存储算子的方法，提高了运算速度，满足了实时性的要求。采用FPGA实现高速数字信号处理的算法具有可行性和优越性，由于FPGA的并行性特点使得算法的实现速度具有很大的提升，因此越来越得到电子工程师们的青睐，但由于文中采用256点基2FFT算法，使数据和性能方面存在缺陷，可以采用1024点FFT提高性能和数据精度。

[1] 王远模,赵宏钟.用FPGA实现浮点FFT处理器的研究[J].国防科技大学学报，2004，26(06):61-64.

[2] 李加元,成立.系统芯片设计的可复用护技术[J].半导体技术，2006，32(0l):15-19.

[3] 刘欢,谢志远.分裂基 FFT算法讨论与改进[J].通信技术，2008，41(03):124-128.

[4] 刘韬,楼兴华.FPGA数字电子系统与开发实例导航[M].北京:人民邮电出版社，2005.

[5] 韩颖,王旭,吴嗣亮.FPGA实现高速FFT处理器的设计[J].电讯技术，2003(02):74-78.

[6] 刘韬,楼兴华.FPGA数字电子系统与开发实例导航[M].北京:人民邮电出版社，2005.

[7] 袁俊全,孙敏琪,曹瑞.Verilog HDL数字系统设计及其应用[M].西安:西安电子科技大学出版社，2002.

[8] 李怀金,王大鸣.数字匹配滤波捕获方法研究与 FPGA实现[J].通信技术，2007,40(05):41-43.

[9] 姚兴波,杨永侠.FFT算法在 OFDM中的应用研究与设计[J]. 信息安全与通信保密,2011(03):58-60.

[10] 李勇,李雀.OFDM系统中多导频的FFT信道估计算法[J].信息安全与通信保密,2008(03):30-33.