水听器混合阵列MUSIC方位估计研究*
赵 锋 奚文骏 袁 钢
(1.海军航空军械修理所 上海 200436)(2.海军航空工程学院兵器科学与技术系 烟台 264001)
1 引言
矢量水听器较之传统的声压水听器,获取了更多的声场信息,这些丰富的声场信息为矢量阵的信号处理带来了更多的选择,也引起了国内外大量学者的关注[1~5]。在应用中,矢量水听器阵列存在一些问题,主要有两点:首先是矢量水听器阵列与声压水听器阵列相比通道数增加了三倍(二维矢量水听器阵列)或四倍(三维矢量水听器阵列),由于大孔径阵列可以增强阵列的方位分辨率和精度,因此通过增加矢量水听器阵元扩展阵列长度必将增加硬件开销、研制费用,信号处理器的复杂度亦有明显增加。其次,矢量水听器阵列对不相关的流噪声和传感器自噪声非常敏感。在阵列中混合配置声压水听器与矢量水听器,是一种解决该问题的有效途径。
本文利用多重信号分类法(MUSIC)[6~7],对五种水听器混合阵列进行研究,分析在不同信噪比、目标相对运动时对方位估计的影响。
2 输出模型
设K个窄带平面波信号入射到由M个水听器与矢量水听器组成的混合阵列上,第i个空间信号的二维空间到达角为Θi=(φi,θi),当第m个阵元为矢量水听器时,输出为
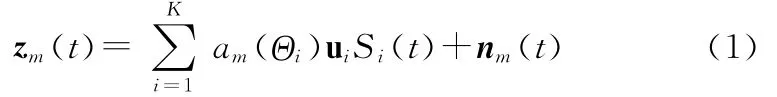
am(Θi)是阵元m对于第i个空间信号的声压响应系数,Si(t)是第i个信号,nm(t)是第m个阵元的声压和振速通道接收到的噪声。
当第m个阵元为水听器时,输出为
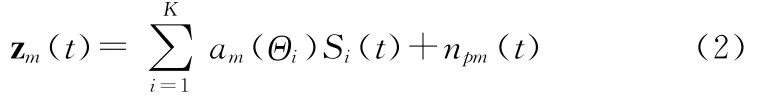
则将该阵列的输出为
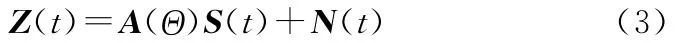
式中N(t)是噪声矢量。
A=[h1,…,hm,…,hM],当第m个阵元为矢量水听器时hm=am(Θi)⊗ui,(⊗表示直积),为水听器时,hm=am(Θi)。
3 阵列的MUSIC算法
设矢量阵接收到的信号和噪声是不相关的,水听器混合阵列的协方差矩阵R,则
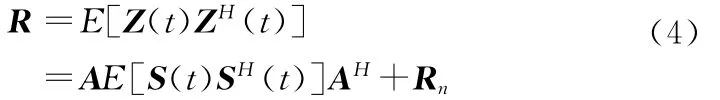
式中Rn=E[N(t)NH(t)]。
根据子空间分解理论,如果信号源的个数少于阵列阵元个数,那么阵列数据的信号分量位于阵列协方差矩阵R的一个低秩空间上。因此对R进行特征分解,并将其特征向量按照特征值得大小降序排列得到
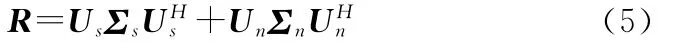
利用信号子空间Us和噪声子空间Un正交特性,可以得到水听器混合阵列的MUSIC空间谱
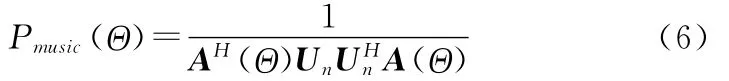
4 混合阵列方位估计
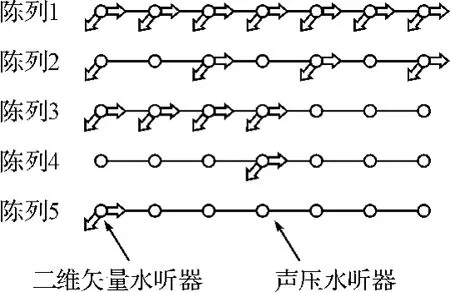
图1 矢量水听器混合阵列配置
考虑一个7元半波长间隔均匀矢量水听器混合线列阵,该五种阵列配置方式如图1所示。为方便,本文只对由二维矢量水听器与声压水听器组成混合阵列进行研究,仿真中只对水平方位角进行方位估计[8~9]。
假设三个非相关复正弦波信号分别从150°、30°与120°方向入射到该线列阵,背景噪声为与信号不相关的高斯白噪声,方位估计使用的数据快拍为200[10]。
4.1 不同信噪比情况下的目标方位估计
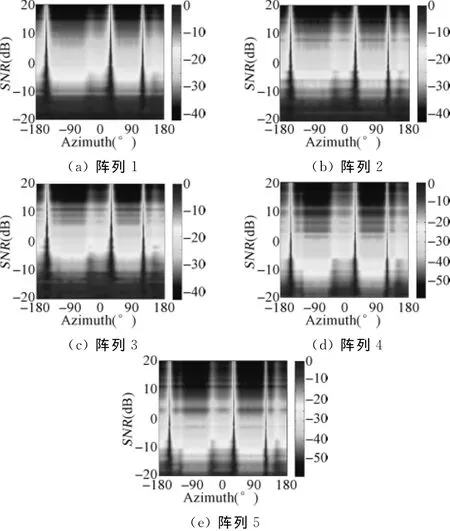
图2 不同信噪比时的MUSIC方位估计
由图2可知:(1)阵列1、2、3在SNR<-15dB时,分辨效果急剧变差。在其它时,分辨效果相差不大。阵列1波束形成效果最好。
2)阵列5比阵列4、5由于有明显的对称波形出现,而且当信噪比足够大时,波束宽度很小,因此这两个阵列比阵列1、2、3相差较大,但相互之间效果相差不大。
4.2 一个目标相对运动时的目标方位估计
信噪比SNR=-5dB,信源1自-150°向位于120°的信源3运动,运动时间为136s,当信源1和3相遇后,共同运动了64s,信源2、3保持静止,方位估计时使用的数据快拍为200。
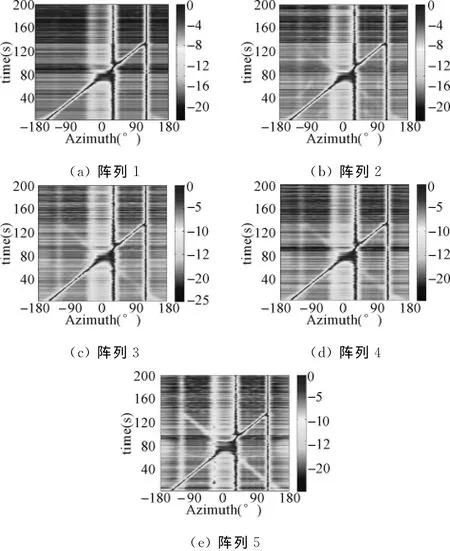
图3 一个目标相对运动时的MUSIC方位估计
由图3可知:
1)阵列1、2、3跟踪目标依次下降,其中阵列1能力最强;阵列2由于间隔配置矢量水听器,因此抑制左右舷模糊效果比阵列3强。
2)阵列4比阵列5抑制左右舷模糊要强许多。
5 结语
对于混合水听器阵列:
1)在有相同数目的矢量水听器的情况下,间隔配置比集中配置要好。
2)在不能确定目标方位的情况下,在中间配置一个矢量水听器比在一端配置要合理的多。
在阵列中,将矢量水听器与声压水听器混合配置不仅可以降低通道数,而且矢量水听器数目的减少,降低了不相关的流噪声和传感器自噪声的影响。因此,研究水听器混合阵列有非常大的工程应用价值。
[1]A.Nehorai,E.Paldi.Acoustic vector-sensor array processing[J].IEEE Transactions on Signal Processing,1994,42:2481-2491.
[2]惠俊英,刘宏,余华兵,等.声压振速联合信息处理及其物理基础初探[J].声学学报,2000,25(4):303-307.
[3]孙贵青,李启虎.声矢量传感器信号处理[J].声学学报,2004,29(6):491-498.
[4]D'Spain G L,et al.Initial analysis of the data from the vertical DIRAR array[C]//IEEE Oceanic 1992Proceedings,1992:346-351.
[5]M.Hawkes,A.Nehorai.Acoustic vector-sensor beamforming and Capon direction estimation[J].IEEE Transactions on Signal Processing,1998,46:269-272.
[6]K T Wong,M D Zoltowski.Self-Initiating MUSIC-Based Di-rection Finding in Underwater Acoustic Particle Velocity-Field Beamspace[J].IEEE J.of Oceanic Engineering,2000,25(2):659~672.
[7]张揽月,杨德森.基于MUSIC算法的矢量水听器阵源方位估计[J].哈尔滨工程大学学报,2004,25(1):30-33.
[8]顾晓东,邱志明,袁志勇.基于改进MUSIC算法的矢量水听器阵列波达方向估计[J].武汉理工大学学报(交通科学与工程版),2009(3):62-64.
[9]周浩,顾晓东,蒋兴舟.矢量水听器阵列MUSIC估计算法研究[J].武汉理工大学学报(交通科学与工程版),2006(4):58-60.
[10]陈晟,程彬彬,赵俊渭.基于改进的MUSIC算法的矢量水听器阵列波达方向估计[J].电声技术,2005(9):132-133.

