一种速率陀螺启动过程的时变增益补偿控制技术＊

雷江涛 张秦南 王立文

（1.西安市76号信箱 西安 710075）（2.西安精密机械研究所 西安 710075）

1 引言

本文控制系统采用继电元件，属于非线性控制系统，可以利用描述函数法进行控制参数设备和稳定性分析［1］，是一种自振荡自适应系统，在控制对象参数和测量元件增益变化时，通过改变自振荡的频率和幅度，可以使得控制系统对输入的传递函数基本保持不变。国外战术导弹也成功地采用了自振荡自适应技术［2～5］，与本文控制系统的工作机理一样，但这类系统适应参数变化的范围较小［6～10］。文中采用的速率陀螺为液浮式机械框架陀螺，由于马达转子存在惯性等原因，初始上电后有一定的启动过程，对水下航行器控制品质有较大影响，甚至会影响系统的稳定性。文献［11］提出机械陀螺的启动特性具有较好的重复性时，可以在实验室通过测试建立启动特性模型，然后在产品中进行补偿以消除启动特性对陀螺性能的影响。借鉴文献［6］的研究思路，在实验室里利用转台建立了速率陀螺的启动特性模型。

为了改善控制品质，有两种方法可供选择，其一是按时间分段进行补偿，如前2s减小控制增益，后2s维持原设计增益，此种方法简单易行，适用于模拟电路构建的控制系统；其二是对陀螺启动过程按时间连续进行补偿或采用时变增益控制技术已实现其稳定控制，此种方法控制效果与陀螺提前启动的相当，适用于数字控制系统。其中，第二种控制方法对陀螺启动时间离散具有较强的适应能力，可显著改善水下航行器控制品质。该方法可用于供电后陀螺有较长启动过程的水下航行器控制系统。

2 速率陀螺启动特性模型和补偿方法

经过测试陀螺启动特性模型为

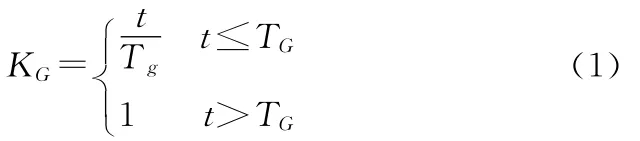
式中：t为从供电时刻开始的时间，s；Tg为速率陀螺启动时间，s；KG为速率陀螺的归一化增益。

启动特性的补偿模型为

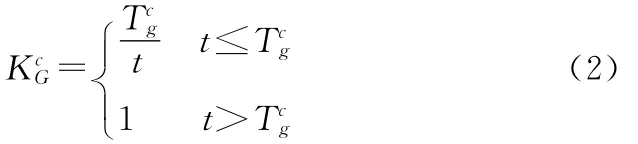
速率陀螺增益补偿后的归一化增益为

式中：Kc为速率陀螺增益补偿后的归一化增益。

当补偿时间等于、小于和大于陀螺启动时间依次称为完全补偿、欠补偿和过补偿。

与陀螺输出平衡的控制信号的时变增益控制系数为

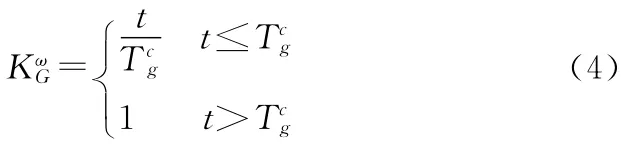
3 控制对象特性分析

3.1 基本控制原理简介

控制对象稳态时处于自振状态，其基本原理是利用振荡进行线性化，当输入信号的有效频带远远小于系统的自振频率时，可以利用等效传递函数近似研究系统的动态过程。经过推导［5］和半实物仿真验证，控制对象的等效传递函数仅与反馈回路的传递函数有关。考虑陀螺启动过程补偿的控制对象的控制方程为

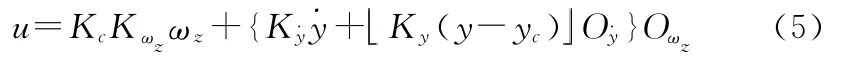
式中：Q˙y为深度微分的限幅值；Oωz为速率的限幅值。

由于限幅器作用，控制系统工作于速率控制、定深度微分控制和定深控制三种工作方式。

3.2 速率控制特性分析

速率控制的等效传递函数为

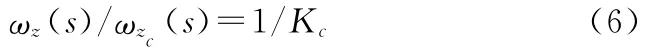
由式（3）可知，与完全补偿相比，欠补偿相当与指令被放大；过补偿相当与指令被缩小。

3.3 定深度微分控制特性分析

定深度微分控制的等效传递函数为

式中：Ty＝KωzKc／VK˙y。

欠补偿相当于时间常数减小，而过补偿相当于时间常数增大。

3.4 定深控制特性分析

定深控制的等效传递函数为

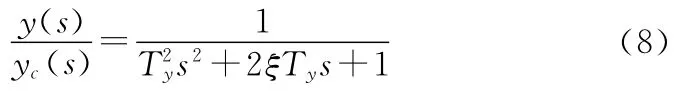
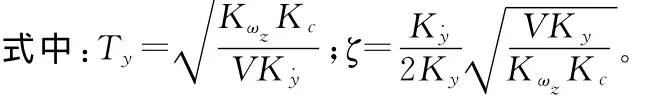
欠补偿相当于时间常数减小、阻尼增大，而过补偿相当于时间常数增大、阻尼减小。

4 仿真计算结果及分析

如图1所示为供电后陀螺提前启动（处于启动好状态）与陀螺启动过程完全补偿情况下的动态曲线对比。

如图2所示为陀螺启动过程完全补偿和时变增益控制下的动态曲线对比。

分析以上结果可知：

如果能对启动过程进行完全补偿，则控制效果与供电后陀螺处于启动好状态的控制效果一样；

当陀螺启动时间大于补偿值，补偿为欠补偿，由于陀螺起着阻尼作用，水下航行器角速率变化快；当陀螺启动时间小于补偿值，补偿为过补偿，由于陀螺起着阻尼作用，水下航行器角速率变化慢。

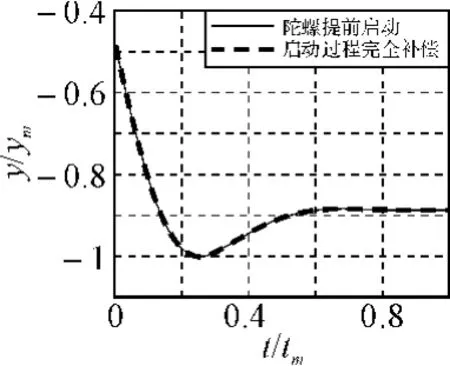
图1 陀螺提前启动与陀螺启动过程完全补偿情况下的动态曲线对比

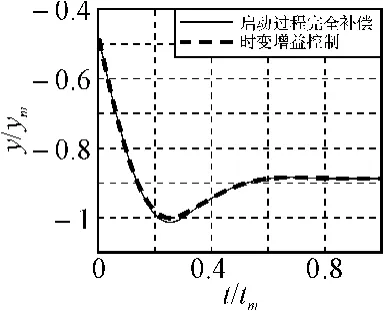
图2 陀螺启动过程完全补偿和时变增益控制下的动态曲线对比

通过大量数学仿真和半实物仿真，针对陀螺启动过程采用增益补偿或时变增益控制技术，加强了速率信号的阻尼作用，可以明显改善水下航行器的控制品质，使得控制系统在各种工况下是稳定的，而且同样工况下数学仿真与半实物仿真吻合，说明数学仿真结果真实可信。以上控制技术经实航验证是可行的。

5 结语

在对陀螺启动特性研究的基础上，采用对陀螺启动特性进行补偿或采用时变增益控制技术，可以明显改善控制品质，实现稳定控制。分析及实验结果表明，对启动过程进行完全补偿，则控制效果与陀螺提前启动好的控制效果一样，由于陀螺起着阻尼作用，与完全补偿相比欠补偿时水下航行器角速率变化快，而过补偿时水下航行器角速率变化慢。

本文提供的方法已经用于有陀螺启动过程而且上电后陀螺才启动的水下航行器稳定控制，在工程上简单、实用。

［1］胡寿松.自动控制原理［M］.第四版.北京：科学出版社，2001，2.

［2］杨军，杨晨，段朝阳，等.现代导弹制导控制系统设计［M］.北京：航空工业出版社，2005，7.

［3］杨军.导弹控制系统设计原理［M］.西安：西北工业大学出版社，1997，12.

［4］钱学森.工程控制论［M］.上海：上海交通大学出版社，2007，1.

［5］陈佳实.导弹控制和控制系统的分析与设计［M］.北京：宇航出版社，1993.

［6］李建辰.水下航行器定位技术［M］.北京：国防工业出版社，2009，9.

［7］国林娜.IMU温度补偿技术研究［C］／／中国惯性技术学会第四次学术年会论文集，1999，11.

［8］徐海刚.惯导双位置对准精度分析［J］.弹箭与制导学报，2009，29（4）.

［9］徐丽娜，邓正隆.陀螺仪启动漂移特性的神经网络建模研究［J］.中国惯性技术学报，1999（1）.

［10］李云.惯性器件快速启动技术研究［C］／／鱼雷控制技术学术研讨会论文集，2006，6.

［11］关国枢.水下航行器非线性控制系统的等效传递函数［J］.信息与控制，1982（1）.