非对称一致性风险测度及其应用

张一安 实 徐照宇

(哈尔滨工业大学，黑龙江 哈尔滨 150001)

合理有效地测度资产风险具有重要的理论与实践意义。在Artzner等人提出的一致性风险测度公理体系中，风险测度应满足单调性、正齐次性、平移不变性以及次可加性等条件。一致性风险测度被提出后，得到了广泛认可，许多学者也相继从不同角度对一致性风险测度展开了各种拓展性研究。Follmer等人放宽了一致性风险测度中的次可加性要求，提出了凸风险测度。Piera用平移递减性和规模递减性代替了一致性风险测度中的平移不变性和正齐次性条件，进一步提出了弱一致性风险测度，相对于一致性风险测度，弱一致性风险测度在理论假设上相对宽松。Rockafellar等人提出了一般离差风险测度，并指出既定形式的一致性风险测度在一定条件下都有与之对应的一般离差风险测度形式。张昇平等人在Artzner和Rockafellar等人研究的基础上，讨论了更多的风险测度属性，提出了类一致性风险测度。

上述研究从不同角度丰富和深化了风险测度的相关理论，但对于投资者来说，现有风险测度公理体系仍存在如下不足:(1)并未充分反映出投资者的风险态度。在现有的风险测度公理体系下，分散化的投资策略要优于非分散化的投资策略。然而Statman等人的研究却表明现实世界中的投资活动并不完全是分散化的，大量投资者采取的投资策略并没有达到理论上应有的分散化程度。(2)只考虑单一的目标收益参考点。Shefrin等人指出投资者实际构建的资产组合是具有层次性的，分配在各层的资产都与不同的目标收益参考点和风险态度相联系。现有风险测度公理体系只考虑存在单一目标收益参考点的情形，难以完整地反映投资者的多层次风险态度。

为了弥补上述不足，本文提出一种新的风险测度——非对称一致性风险测度，这一风险测度在多参考点的情形下考虑了投资者对收益双向波动的不同风险态度，实现了对现有风险测度公理体系的补充与完善。本文进一步给出了一类非对称一致性风险测度的函数形式，构建了相应的投资组合优化模型，最后通过实证研究说明新的风险测度在实践中的可行性与合理性。

一、非对称一致性风险测度的提出

记τi为投资者的第i个目标收益参考点，其中i=1，2，…，M，而所有参考点组成的参考点向量则记为 T=(τ1，τ2，…，τM)。对于单独的 τi来说，资产 X 的风险为 ρ(X，τi)，记(X，τi)=ρ(min(X，τi)，τi)，表示小于 τi的 X 分布所带来的风险，ρ+(X，τi)= ρ(max(X，τi)，τi)则表示大于τi的X分布所带来的风险。对于所有的参考点来说，资产X的总体风险是ρ(X，τi)的函数，记为 ρ(X，T)=G(ρ(X，τi)，…，ρ(X，τM))。此外，记ρ-(X，T)=G(ρ-(X，τ1)，…，ρ-(X，τM))，ρ+(X，T)=G(ρ+(X，τ1)，…，ρ+(X，τM))，分别对应于只考虑 ρ-(X，τi)和ρ+(X，τi)时的总体风险。

定义1 若风险测度ρ满足如下的条件(M)、(ZR)、(TR)、(LCV)、(LCC)和(IC)，则称ρ为非对称一致性风险测度。

(M)单调性(Monotonicity):ρ(X，T)≤ρ(Y，T)，∀X≥Y;ρ(X，τi)≤ρ(X，τi+ δ)，∀δ≥0;ρ(X，T)≤ρ(X，T+ Δ)，Δ =(δ1，δ2，…，δM)，δi≥0，i=1，2，…，M

(ZR)零风险性(Zero Risk):ρ(δ，δ)=0，δ∈R

(TR)平移递减性(Translation Reduction):ρ(X+ δ，T)≤ρ(X，T)+ ρ(δ，0)，∀δ≥0

(LCV)局部凸性(Local Convexity):ρ-(λX+(1- λ)Y，T)≤λρ-(X，T)+(1- λ)ρ-(Y，T)，0≤λ≤1

(LCC)局部凹性(Local Concavity):ρ+(λX+(1- λ)Y，T)≥λρ+(X，T)+(1- λ)ρ+(Y，T)，0≤λ≤1

(IC)不灭性(Incorruptibility):ρ(X+ δ，τi+δ)= ρ(X，τi)，δ∈R

上述条件的经济意义如下:

(M)单调性:一方面，在投资目标收益相同的情况下，若一项资产X优于另一项资产Y，即前者随机回报的各分量大于或等于后者随机回报对应的分量，则前者的风险不大于后者。另一方面，同一资产对于不同的目标收益来说，其风险大小也有所不同，较高目标收益实现难度较大，因此其对应的风险也较大。

(ZR)零风险性:如果资产具有与目标收益参考点相等的确定性收益，那么其风险为0。

(TR)平移递减性:结合单调性和零风险性，对于∀δ≥0，有 ρ(δ，0)≤ρ(δ，δ)=0，于是 ρ(X+δ，T)≤ρ(X，T)+ ρ(δ，0)≤ρ(X，T)+ ρ(δ，δ)=ρ(X，T)，这样平移递减性就意味着在现有的资产中加入具有确定性非负收益的资产δ后，所形成的新资产(组合)的风险将不会增加。

(LCV)局部凸性:对于收益低于参考点的分布所对应的风险来说，其在资产组合中的总体水平不大于其在各项资产中的分量之和，也就是说这一部分风险可以通过分散化投资得以降低。

(LCC)局部凹性:对于收益高于参考点的分布所对应的风险来说，其在资产组合中的总体水平不小于其在各项资产中的分量之和，也就是说这一部分风险可以通过集中化投资得以降低。

(IC)不灭性:如果目标收益和资产收益发生同向等量变化，那么资产的风险将不发生变化。另一种解释是资产的风险不能通过投资其他无相关性资产得以消灭。

二、一类非对称一致性风险测度的函数形式

首先，用如下的式(1)测度资产X相对于单参考点τi的风险:

其中ci(x)定义如下:

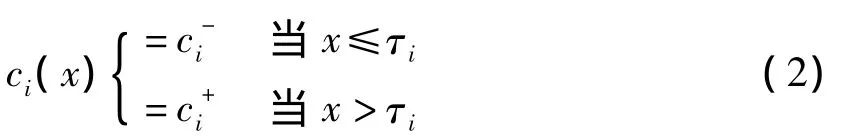
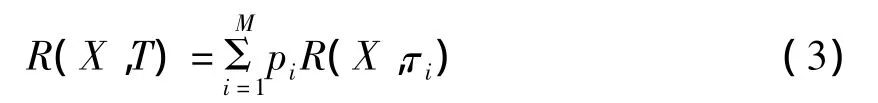
其中pi可以理解为R(X，τi)在总风险中所占的比重，由投资者的主观风险态度所决定。容易证明，式(3)所对应的风险测度是非对称一致性风险测度。

三、非对称一致性风险测度在投资组合优化中的应用

1.投资组合优化模型的建立

采用式(3)测度风险时，以投资总体风险最小化为目标的投资组合优化问题如下:

其中 CVaR*α和 μ*均为给定的数值。约束(5)中的条件在风险价值CVaRα(X，0)是常见的一致性风险测度，其含义为:在置信水平α下，若资产X的最大损失为 VaRα(X，0)，则 CVaRa(X，0)表示损失超过VaRα(X，0)时的平均值。问题P1采用CVaRα(X，0)对极端损失进行控制，主要是为了满足监管当局和清算机构等行为主体的相关要求。约束(6)则对应于投资者的最低期望收益要求。

在实际问题中，对于X的S个离散样本x1，x2，…，xS，可以通过来近似计算 R(X，τi)，此时pici(xk)(xk-τi)。当X由N种资产构成时，记其中第n种资产所占比重为用来控制该种资产持有量。若第n种资产收益的第k个样本为，问题P1的优化目标变为，而约束(6)则变为此外，根据Rockafellar等人的研究，CVaRα(X，0)可以通过如下的问题P2求出:

这样，问题P1就变为如下形式:

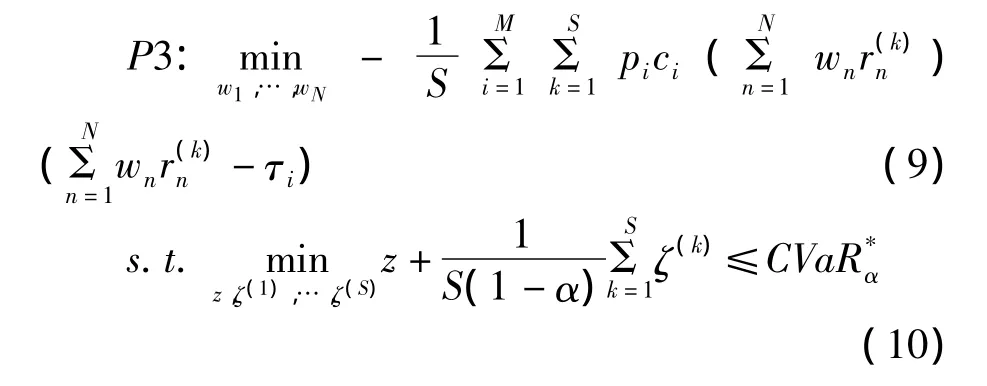
2.实证分析

本文选择不同地区、不同种类(股票、债券和贵金属)的10种资产构建投资组合，采用1992年3月31日至2009年9月30日的香港恒生指数、深证综合指数、上证综合指数、费城金银指数、美国30年期国债指数、道琼斯工业平均指数、纳斯达克综合指数、德国DAX指数、巴黎CAC指数以及新加坡海峡时报指数的月收益率作为10种资产投资收益的历史数据，数据来源于锐思金融研究数据库(www.resset.cn)。根据上述数据的基本情况，有N=10，S=211，同时设定两个参考点，即M=2。利用Matlab7.8.0软件在不同的参数设定下对问题P3进行求解，以考察各参数变化对最优投资组合的影响，计算结果见图1。

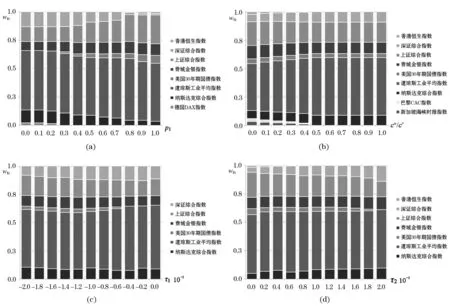
图1 不同参数设定下的最优投资组合

对计算结果的进一步分析如下:

1)p1减小时，最优投资组合的分散化程度随之降低，反之，当p2减小(p1增大)时，投资组合的分散化程度应该随之增加，上述计算结果恰好反映了这一情形，是符合实际情况的。

2)根据计算结果，当投资者更加偏好获取超额收益，即c+/c-增大时，最优投资组合的分散化程度也随之降低，这与实际情况是相符的。

3)相对集中化的投资有利于较高目标收益的实现，因此当τ1和τ2增大时，最优投资组合的集中化程度增加，即分散化程度降低，这一情形也在计算结果中得到了反映。

综上，在多参考点的情形下，计算结果如实地体现了以下因素对最优投资组合的影响:投资者对不同参考点对应风险所持的风险态度、对参考点以上收益波动的偏好程度、参考点的设定。

四、结论

在已有的风险测度公理体系下，投资者对目标参考点以上收益波动的风险态度不能得到合理反映，并且单一参考点的设置也不能与投资者的多层次风险态度相对应。为了弥补这些不足，本文提出非对称一致性风险测度，这一风险测度在多参考点的情形下通过局部凹性和局部凸性分别描述了投资者对收益双向波动的不同风险态度，与此同时已有风险测度公理体系中的平移不变性、零风险性等条件也被弱化，使其更符合实际情况。虽然本文从投资者的角度定义了新的风险测度，但进一步的分析表明其应用并不局限于投资者，在一定条件下也适用于监管当局等其他行为主体。

此外，本文还给出一类非对称一致性风险测度的函数形式，并以其为基础构建了投资组合优化模型，同时结合具体数据进行实证研究。投资者的多层次风险态度、对参考点以上收益波动的偏好程度、参考点的设定等因素对最优投资组合的影响在计算结果中都得到如实反映，这表明本文提出风险测度和构建的投资组合优化模型在实践中是合理可行的。

［1］ Artzner P，Delbaen F，Eber J M，Heath D.Coherent measures of risk［J］.Mathematical Finance，1999，9(3):203-228.

［2］ Hans Follmer，Alexander Schied.Convex Measures of Risk and Trading Constraints［J］.Finance and Stochastics，2002，4(6):429-447.

［3］ Piera Mazzoleni.Risk Measures and Return Performance:A Critical Approach［J］.European Journal of Operational Research，2004，2(155):268-275.

［4］ R.Tyrrell Rockafellar，Stan Uryasev，Michael Zabarankin.Generalized Deviations in Risk Analysis［J］.Finance and Stochastics，2006，1(10):51-74.

［5］ 张昇平，吴冲锋.权益人视角下基于期权定价理论的类一致性风险测度研究［J］.系统工程理论与实践，2007，9(27):9-16.

［6］ Meir Statman.The Diversification Puzzle［J］.Financial Analysts Journal，2004，4(60):44-53.

［7］ 徐龙炳.中国股市机构投资者多账户交易行为研究［J］.经济研究，2005(40):72-80.

［8］ Valery Polkovnichenko.Household Portfolio Diversification:A Case for Rank-Dependent Preferences［J］.Review of Financial Studies，2005，4(18):1467-1502.

［9］ William N.Goetzmann，Alok Kumar.Equity Portfolio Diversification［J］.Review of Finance，2008，3(12):433-463.