铁路简支槽形梁横向抗弯设计方法研究

田 卿，刘 丹，戴公连

(中南大学土木建筑学院，长沙 410075)

1 概述

预应力混凝土槽形梁是一种下承式受弯构件，主要由桥面板、主梁及端横梁等部分组成。

列车荷载作用在桥面板上，由于单向板作用，荷载主要沿横向传递至两侧主梁，再沿纵向传递至两端支座，所以桥面板厚度直接取决于横向抗弯设计[1-3]。由于桥面板支承在主梁和端横梁上，板端受到弹性约束[4]，使其受力特征介于简支和固端二者之间，必须考虑整体作用才能准确描述其横向受力。一般能考虑槽形梁整体作用的研究方法包括:函数解法[1]、加权余量法[5]、梁格模型[6]、梁-板空间有限元模型[7，8]、空间板壳模型[9]、三维实体有限元模型[4，10]以及试验模型[3，10-12]，这些方法都可以在一定范围内解决横向设计问题，但较为繁琐或成本较高。因此，对于常规槽形梁，日本、前苏联以及我国均提出了简化算法。

结合在建的沅江特大桥——48 m铁路预应力混凝土简支槽形梁，采用三维实体有限元整体模型分析其横向受力，与简化计算方法作对比，探讨简化方法的适用性及改进意见，并给出对于类似简支槽形梁的设计建议。

2 结构方案介绍

本桥为普通铁路高架桥，如图1所示。跨径48 m，全长49.2 m，单线，有砟，截面为直墙式，桥面等宽。桥面板厚0.55 m，端横梁厚0.8 m，纵向长2 m。跨中腹板厚0.4 m，端部加厚至0.73 m。设置了3 m渐变段，截面由跨中到支点的所有变化均在此渐变段内完成。

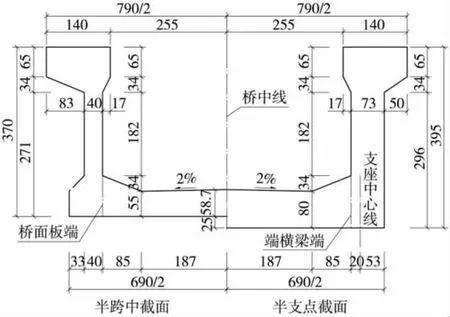
图1 48 m槽形梁方案横截面(单位:cm)

3 横向弯矩分析

3.1 简化计算方法

3.1.1 桥面板简化计算方法

我国针对跨度分别为20 m和24 m的2座槽形梁的研究表明，对于四点支承的槽形梁，每米长板段桥中线处的横向弯矩可由下式估计[1，13]

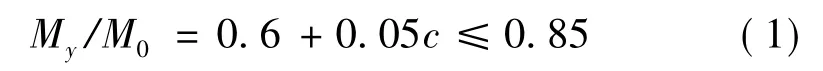
式中:c为桥面板长宽比;M0为在设计荷载作用下，按计算跨度为两腹板中心距的简支梁计算得到的跨中弯矩;My为桥面板跨中计算横向弯矩。

而桥面板板端最大横向弯矩由下式估计板端负弯矩:

板端正弯矩:

式中，M1为在设计荷载作用下，按计算跨度为两腹板中心距的固端梁计算得到的固端弯矩。

而《日本高速铁路铁道结构物设计标准》中规定的槽形梁桥面板横向弯矩计算方法为[17]:最大跨中正弯矩，按简支单向板计算;最大支点负弯矩，按最大跨中正弯矩的1/2计算;最大支点正弯矩，按最大跨中正弯矩的1/4计算。

显然，无论对于跨中还是板端弯矩的计算，日本规范均偏于保守。

3.1.2 端横梁简化计算方法

我国学者认为，由于端截面刚度增大，端横梁不仅承受直接作用于其本身的荷载，也承担了一部分附近桥面板的荷载。故提出端横梁跨中正弯矩仍按简支梁计算，其荷载模式如图2所示。其中a为主梁内侧净距，b为端横梁宽度。端横梁计算截面不考虑过渡段。梁端正负弯矩均取跨中正弯矩的0.2倍[1，13]。

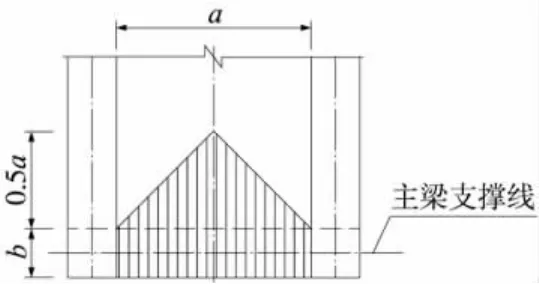
图2 我国学者建议端横梁荷载范围

3.2 有限元分析

3.2.1 有限元模型及荷载工况

采用ANSYS软件进行空间有限元整体分析，混凝土采用20节点实体单元 solid95模拟，全桥共约110 000个节点，23 000个单元。边界条件采用实际4点支承。分析荷载包括自重、二恒及列车活载。列车活载采用中-活载。基本有限元模型见图3。

图3 空间有限元模型正等轴测图

3.2.2 有限元分析结果

在梁体自重及二期恒载作用下，全桥每延米横向弯矩沿纵向分布如图4所示。方向以下缘受拉为正。

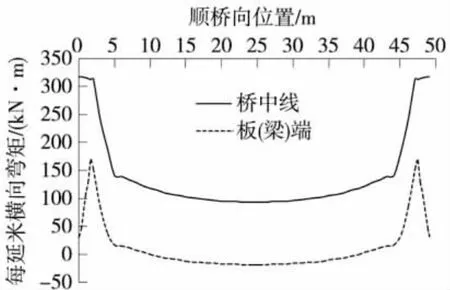
图4 恒载作用下桥中线及板端横向弯矩

图4显示了横向弯矩在桥面板板内呈现抛物线式分布，且端横梁内由于应力集中弯矩比板内大得多。

对于单线桥，取作用在桥面板横向宽度a上合力为1 N的线荷载，沿线路纵向移动，可得到各点内力的影响线。活载分布宽度a按自枕木底面向下45°扩散取为3.14 m。图5为顺桥向典型位置(跨中及1/4跨，分别以L/2和L/4表示，下同)桥中线与板端横向弯矩影响线。

分析横向弯矩影响线可知。

(1)对于桥中线任意位置的横向弯矩，满布活载均为最不利情况;

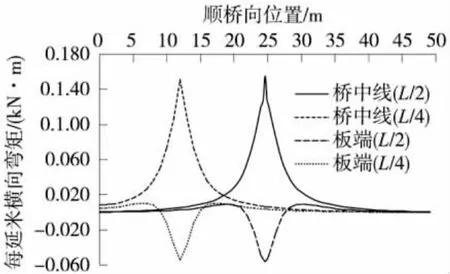
图5 横向弯矩影响线

(2)板端弯矩影响线同时存在正负区段:在活载作用点附近为负，稍远处变为正。这就导致最不利弯矩需要单独在影响线同号区域加载才能得出。

影响线形成原因可作如下解释:当单位荷载作用在桥面某位置时，该处截面发生的变形表现为桥面板横向挠曲及两侧主梁同时向内侧转动，然而稍远处未受到荷载作用的截面将阻止该截面发生变形，这就导致活载作用点附近板端出现负弯矩，稍远处板端出现正弯矩。

根据影响线进行加载，可得到活载作用下桥中线及板(梁)端部最不利弯矩，如图6所示。

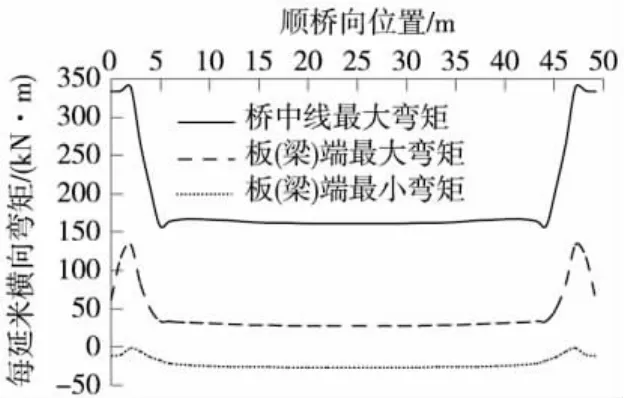
图6 活载作用下横向弯矩分布

对上述恒、活载作用结果进行叠加，得到恒载+最不利活载作用下横向弯矩分布，如图7所示。

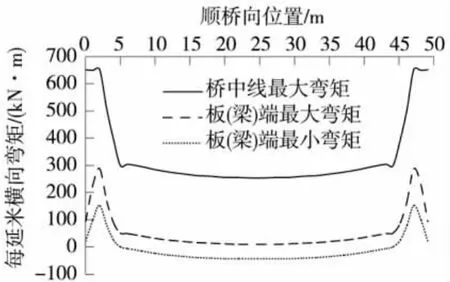
图7 恒、活载作用下横向弯矩分布

分析上述结果，在荷载作用下每延米横向弯矩分布有如下普遍规律。

(1)端横梁由于刚度大，分担了桥面板荷载，使其横向正弯矩很大而负弯矩很小，且其弯矩量值总是比板内大的多;这也是对端横梁和桥面板采取不同计算方法的原因。渐变段作为由桥面板到端横梁的过渡，其弯矩也在二者之间线性变化。

(2)桥中线横向弯矩在桥面板内分布线形在恒载作用下为抛物线(主要由自重引起)，最不利活载作用下近似平直线，叠加后仍然是抛物线，纵向跨中处出现极小值。

(3)板端正负横向弯矩始终呈抛物线分布，同样在L/2处出现极小值。

(4)端横梁内横向弯矩始终接近线性分布，且基本只会出现正弯矩。虽然最不利活载作用下梁端会产生负弯矩，但量值很小，会被恒载抵消。

上述横向弯矩分布规律显示，槽形梁的横向设计在顺桥向有4个控制位置:桥跨最末端、端横梁与过渡段交汇处、桥面板与过渡段交汇处和跨中(分别如图8中1－1、2－2、3－3、4－4截面，以下分别简称位置1、2、3、4)。前两者出现端横梁横向弯矩的极值点，后两者出现桥面板横向弯矩的极值点。

图8 横向设计在顺桥向控制位置示意

3.3 有限元分析与简化方法对比

对于桥面板，现将上述恒、活载作用下各种计算方法所得的控制横向弯矩(图8中3、4截面间最大弯矩)汇总于表1，并作简单比较。

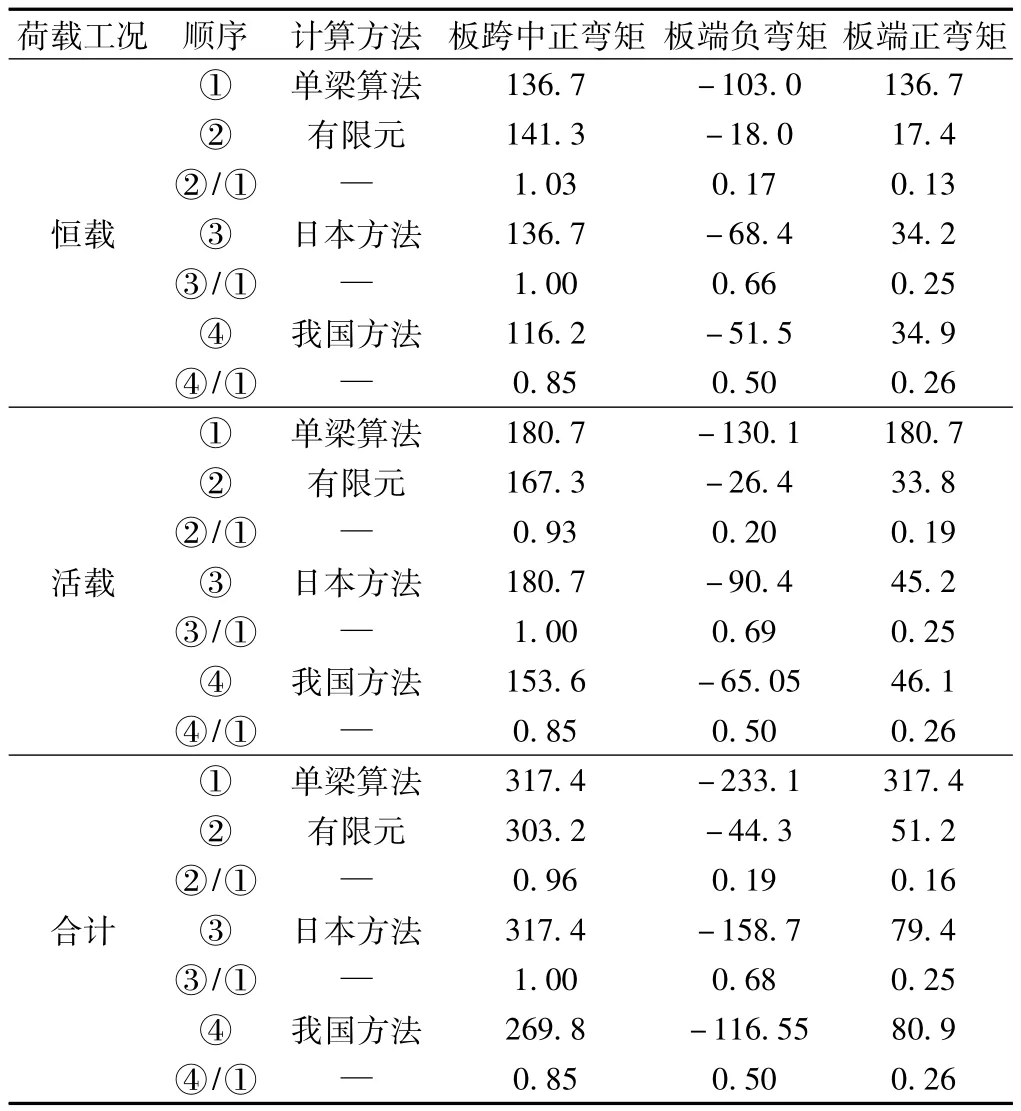
表1 各方法计算桥面板每延米横向弯矩结果对比kN·m

表1中显示出一些指导桥面板设计的结论。

(1)对于桥面板最大横向弯矩，恒、活载共同作用下最不利处可达0.96倍简支梁跨中弯矩，尤其是恒载单独作用下此比值甚至略大于1。可见在最不利位置，桥面板受力状况是可以与简支梁相当的，按简支梁设计并不保守。我国方法认为上述比值不会超过0.85，显得对桥面板跨中弯矩估计不足。事实上，2种简化方法均仅针对跨中桥面板，而本桥跨中桥面板桥中线处最大横向弯矩在恒活载共同作用下，仅相当于0.8倍简支梁跨中弯矩，说明我国方法是有一定理论依据的，且比较精确，只是对于本桥，桥面板内的桥中线横向弯矩呈抛物线分布，设计控制点在两端而不在跨中，且相差较大，此时我国方法已不太适用。

(2)对于本桥板端负弯矩，恒、活载作用下不超过0.2倍固端梁端部弯矩，而按日本规范(0.68倍)和我国方法(0.5倍)估计，均过于保守了。

(3)对于本桥板端正弯矩，恒、活载作用下与简支梁跨中弯矩比值分别为0.13、0.19，而按日本规范计算为0.25，我国方法计算为0.26。可见2种方法均比较合理，也有一定的富余。

对于端横梁，其控制设计弯矩取图8中1、2截面间最大弯矩，各计算方法进行比较见表2。

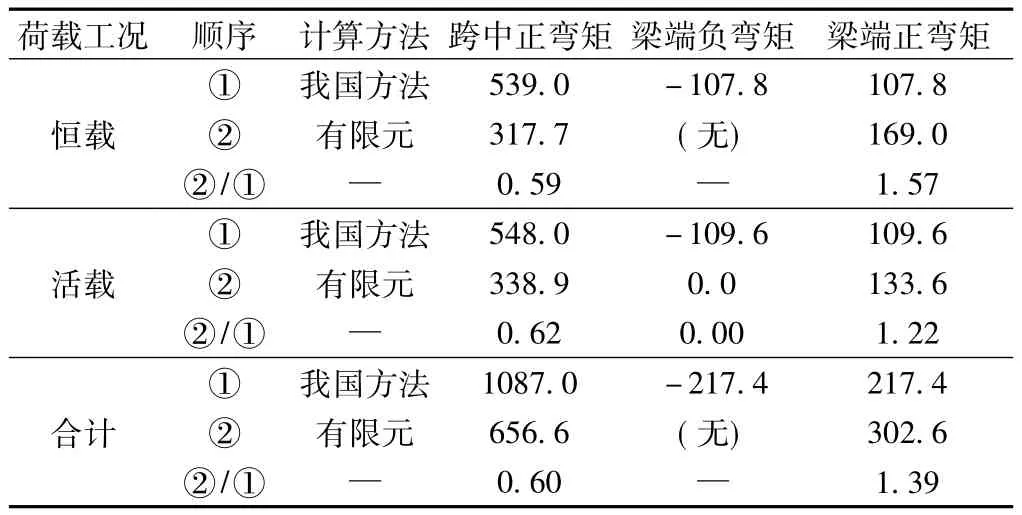
表2 各方法计算端横梁每延米横向弯矩结果对比kN·m

从表2同样可得出一些指导端横梁设计的结论。

(1)按我国学者提出的荷载模式计算跨中正弯矩，有40%的富余。

(2)对于梁端负弯矩，我国方法统一考虑为0.2倍跨中正弯矩。但实际梁端负弯矩量值很小，基本可以忽略。

(3)梁端正弯矩同样按0.2倍跨中正弯矩计算则对实际情况估计不足。端横梁为桥面板提供板端负弯矩的同时，自身梁端将承受正弯矩，由后面的分析可看到，横梁刚度越大，梁端正弯矩也越大。本桥横梁并不算厚(约1.45倍桥面板厚)，但梁端正弯矩已经大大超过0.2倍跨中正弯矩，达到约0.3倍跨中正弯矩。

需要指出的是，无论对于桥面板或端横梁，控制设计的最主要因素还是桥中线最大正弯矩，这个值直接决定了板(梁)厚度和钢筋(或预应力)用量。

上述分析可以说明，简化方法对于本桥并不是完全适用，甚至不能保证一定是偏安全的，主要原因就是忽略了一些能够影响横向弯矩分布的因素。

3.4 横向弯矩的影响因素分析

结合前面的分析可知，影响槽形梁横向弯矩分布的主要因素是半框架截面的横向刚度，确切地说，是桥跨端部截面对桥跨中段截面的相对横向刚度。半框架截面的横向刚度主要由2部分组成:底板的横向弯曲刚度和两侧主梁的扭转刚度。能对这些刚度产生影响的，主要是桥面板和端横梁厚度、主梁腹板厚度和横隔板设置情况。

经计算验证，腹板厚度增加，桥面板横向弯矩稍有增大，而端横梁横向弯矩略微减小。设置主梁横隔板后，横隔板附近局部区域横向弯矩有一定程度的改善。但计算同时表明，以上2种变化虽然改变了主梁刚度，但对横向弯矩影响非常有限，远远达不到简化方法的计算值。

接下来考察底板刚度对横向弯矩的影响。横向内力的分布只与端截面对跨中截面的相对横向刚度有关，因此可以通过调整端横梁厚度来调整横向弯矩的分布。

图9给出不设置端横梁时，恒载+最不利活载作用下桥中线最大横向弯矩分布。此时，板内横向弯矩分布不再均匀，最大值比按简支梁计算的值还大的多，达到最小值的1.59倍，桥面板处于很不利的工作状态，而且配筋难度大。而原模型设置了厚80 cm的端横梁，则板内横向弯矩分布均匀，最大值与最小值很接近，前者为后者1.18倍。

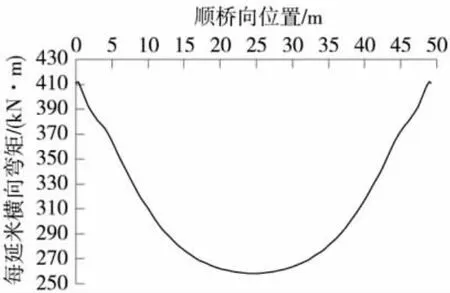
图9 不设端横梁时桥中线最大横向弯矩

本桥原端横梁厚80 cm，日本规范认为端横梁的合理厚度应为桥面板的1.5～2.0倍[17]，即82.52～110 cm，可见，本桥端横梁是偏薄的。为估计端横梁对横向弯矩的影响，可通过在合理范围内调整端横梁厚度，观察4个控制点横向弯矩的变化。图10～图12给出了恒载+最不利活载作用下，端横梁取不同厚度时控制点横向弯矩的变化。此时桥面板厚度是不变的。

端横梁厚度的增加，就意味着端横梁对桥面板的相对横向刚度增大，从而使端横梁对桥面板的约束增强，直接表现就是:桥面板横向弯矩量值减小，且分布趋于更均匀;而端横梁横向弯矩量值有增大趋势。分析图10～图12可估计这种影响的大小。

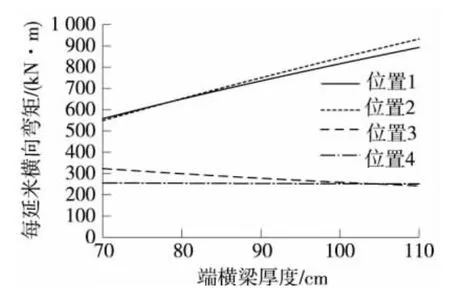
图10 不同端横梁厚度时桥中线最大横向弯矩

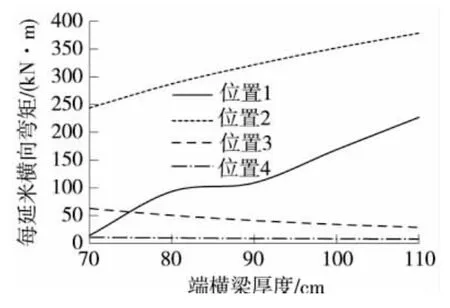
图11 不同端横梁厚度板(梁)端最大横向弯矩

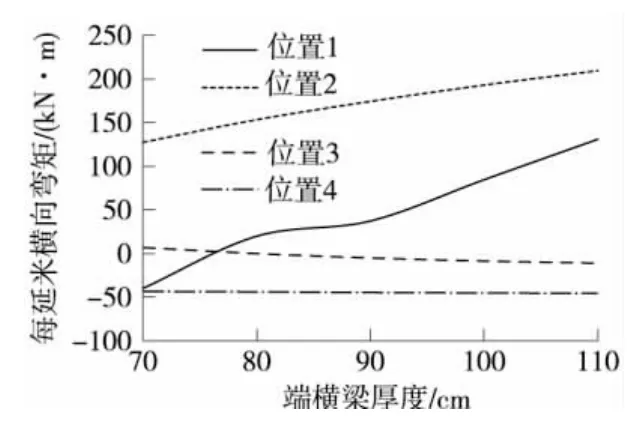
图12 不同端横梁厚度板(梁)端最小横向弯矩

(1)桥中线横向弯矩:随着端横梁厚度的增加，位置3和位置4桥中线横向弯矩同时减小且逐渐接近，二者之间差值由105.2 kN·m变化至－8.6 kN·m，说明桥面板横向弯矩分布趋于均匀。同时，桥面板设计控制弯矩(上述二者之中较大者)下降，由1.15倍简支梁跨中弯矩下降到0.79倍，产生的经济效益是可观的。这也说明，一旦设置了强大端横梁(对于本桥，端横梁厚度至少需要100 cm)，桥面板横向弯矩分布均匀，以跨中(位置4)为设计控制点是可行的。另外，端横梁厚度增加也导致其自身桥中线横向弯矩迅速线性增大，弯矩变化范围从550.3 kN·m到932.0 kN·m，此增量小部分来源于本身自重增加，大部分来源于刚度增加导致承担荷载的增加，使其越来越接近我国简化方法的计算值。因此，实际端横梁刚度越小，则简化方法富余越大，越不经济。

(2)板(梁)端最小横向弯矩:板端负弯矩未发生实质性变化，基本都表现为正弯矩，只有厚度70 cm才会出现很小的负弯矩，不影响设计。

(3)板(梁)端最大横向弯矩:与桥中线横向弯矩一样，板端横向弯矩同样随端横梁厚度增加而减小，且趋于均匀。端横梁自身端部最大弯矩随厚度增加线性增大，增幅很大，但此弯矩不会控制钢筋或预应力的设计，仅关系到横向预应力锚固位置，这种情况下按0.3倍跨中正弯矩考虑还是比较适宜的。

3.5 横向弯矩影响因素总结

首先，主梁(包括腹板，横隔板等)对于横向弯矩而言是次要影响因素，而简化计算方法考虑了足够的富余，足以把主梁的最不利影响包含在内，因此，在横向设计中通常可以忽略主梁影响。

端横梁是横向弯矩的主要影响因素，通过提高端横梁对桥面板的相对横向刚度，可以更有效地约束桥面板，使其横向弯矩减小且分布更加均匀，减少桥面板钢筋或预应力用量，总体来说是更经济的。并且，只有在端横梁刚度足够大的基础上，我国学者建议方法才是经济适用的。不难看出，对于桥面板的计算，日本规范的方法富余很大，我国方法是一种比日本规范更为精确的方法，但其针对位置是桥跨中央，当桥面板内横向弯矩沿纵向分布不太均匀时，这种方法就不适用了，而桥面板横向弯矩分布均匀的要求就是端横梁足够强大。对于端横梁的计算，我国学者提出的方法保证了一定的富余量，可供参考。最后，对于端横梁本身，增加厚度也是有利于其受力的。虽然增加厚度使其自身横向弯矩迅速增加，但其抗弯刚度也大幅增加，在恒活载共同作用下，端横梁厚度从70 cm增加至110 cm的过程中，弯矩产生的截面边缘应力由6.85 MPa下降到4.43 MPa，对其受力显然是有益的。总之，在合理范围内设置较强的端横梁是有好处的。根据日本规范，端横梁厚度与桥面板厚度比例在1.5～2.0之间较为适宜，比例过大则增加端横梁厚度的优势将不明显，且增加了端横梁材料用量。对于本桥而言，最适宜的端横梁厚度实际为100 cm，相当于约1.8倍桥面板厚。

4 结论与建议

通过对国内外槽形梁现状的研究及本文的实例分析，可得以下结论和建议。

(1)竖荷载作用下，桥面板的横向弯曲在一定程度上受到约束，减少了桥中线横向弯矩，但约束大小与很多因素相关，总的来说可分为直接因素和间接因素。间接因素主要是荷载状况。满布荷载时桥中线横向弯矩最大，是桥面板的设计控制弯矩;桥面板局部作用荷载时，板端可能出现正、负弯矩，但量值很小。直接因素主要是桥面板和端横梁的横向抗弯刚度。

(2)日本规范对于桥面板简化计算的规定比较保守，我国学者提出的桥面板计算方法相对更精确，但这2种方法计算桥中线最大横向弯矩时，都有一定适用条件:必须设置刚度足够大的端横梁，使桥面板横向弯矩分布沿纵向分布较均匀。桥中线最大横向弯矩呈抛物线分布，而简化方法主要针对跨中，因此只有桥面板横向弯矩分布均匀、极大值与极小值差别不大时才能适用。对于本桥，端横梁厚度若小于75 cm(1.36倍桥面板厚)，2种方法都对最大弯矩估计不足;端横梁厚度若在75～95 cm(1.36～1.73倍桥面板厚)，日本规范的规定是可行的，而我国方法估计不足;端横梁厚度若超过95 cm，2种方法都可行，但我国方法更准确。

(3)端横梁最大横向弯矩的简化算法，我国学者建议的模式可以参考，但同样没有考虑端横梁刚度的影响。本文建议经济合理进行槽形梁横向设计的原则是:弱桥面板，强端横梁。

(4)桥面板端正负弯矩一般不会控制设计，但会影响横向预应力锚固位置。考虑到实际板端正负弯矩的量值相差并不大，本文认为，预应力锚固点的重心设置在板端面中性轴附近是一种合理的选择。

(5)端横梁端正负弯矩同样不控制设计，但能对其准确估计同样是有好处的。本桥梁端基本不产生负弯矩，正弯矩大概为0.3倍跨中正弯矩，因此本文认为取0.3倍跨中正弯矩是合适的，这也与桥面板端正弯矩简化取值保持了一致。

[1]胡匡璋，江新元，陆光闾.槽形梁[M].北京:中国铁道出版社，1987.

[2]胥为捷，薛伟辰.预应力混凝土槽形梁的研究与应用[C]∥首届全国建筑结构技术交流会.北京:2006:100-105.

[3]张鹏.轨道交通槽形梁性能分析及优化研究[D].上海:同济大学，2009.

[4]陆光闾.连续铁路槽形梁桥空间作用分析[J].铁道学报，2000，22(S1):42-46.

[5]邓勇，胡匡璋，江新元.用加权余量法分析槽形梁空间作用[J].上海铁道学院学报，1990，11(1):37-48.

[6]胡俊.闽江桥道碴桥面槽形梁结构受力分析[D].长沙:中南大学，2007.

[7]陈铭.铁路预应力混凝土连续槽形梁研究[J].铁道标准设计，2009(6):39-41.

[8]刘建萍.上海轨道交通6号线槽形梁设计[J].铁道标准设计，2009(12):55-57.

[9]王玉田，姜福香，谭小群，等.预应力混凝土槽形简支梁内力分析方法研究[J].青岛理工大学学报，2007，28(2):14-17.

[10]王淼，顾萍.预制主梁现浇道床板的槽形梁研究[J].同济大学学报:自然科学版，2003，31(7):808-812.

[11]陆光闾，秦永欣，李凤琴.我国两座槽型梁桥的现场综合性试验[J].铁道工程学报，1985(1):147-157.

[12]李丽，王振领，张宇宁.地铁高架槽形梁足尺模型破坏试验与空间分析研究[J].中国铁道科学，2005，26(5):31-35.

[13]江新元，胡匡璋.槽形梁竖荷载作用分析及常规计算原则[J].铁道工程学报，1985(3):118-129.

[14]尤元霞，阎贵平，许丽娜.某轻轨高架桥两种计算结果的对比分析[J].山西建筑，2007，33(11):282-283.

[15]林文泉.槽形梁桥在城市轨道交通中的应用探讨[D].北京:北京交通大学，2005.

[16]尤元霞.预应力RPC槽型梁的极限承载力及优化设计研究[D].北京:北京交通大学，2007.

[17]日本高速铁路铁道结构物设计标准.混凝土结构物[M].铁四院科技信息中心，译.武汉:铁四院科技信息中心，1995.