基于Excel三次样条函数的求解

张远双

（武汉船舶职业技术学院，湖北武汉 430050）

在计算机辅助船舶设计和建造中，三次样条函数是船体型线典型的数学表达。在平面直角坐标系xoy中，给定若干个型值点Pi（xi，yi）（i＝0，1，2，…，n），船体型线可用三次样条函数描述为［1］：

式中：mi·i＋1为一阶差商；

ci为三次样条函数的系数，根据节点关系式和端点条件，系数ci的求解表达式可表示为：

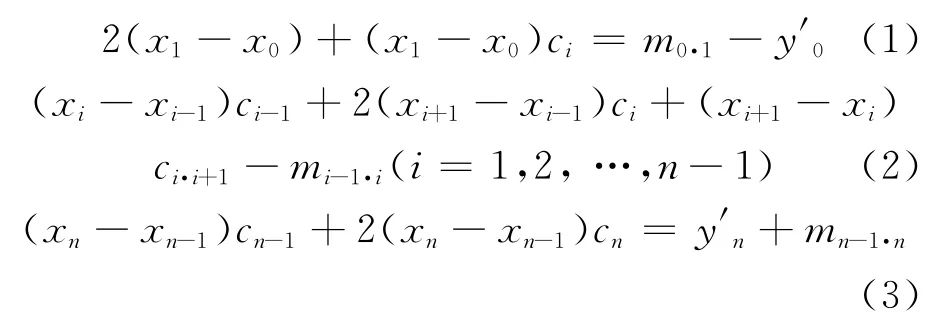
用三次样条函数描述船体型线的关键在于求解三次样条函数的系数。

1 线性方程组求解方法分析

系数ci的表达式（1）、（2）、（3）可化为n元一次方程组，根据数学知识将线性方程组改写成矩阵方程AX＝B，系数方阵A为平行于对角线的三列稀疏矩阵，若其逆阵存在（即系数行列式的值不为零），则方程组有唯一解X＝A－1B。

用常规追赶法［2］求解上述n元一次线性方程组，随n值的增大，求解过程愈复杂，具有相当难度。Excel是目前非常流行且计算功能强大的电子表格软件，使用Excel的规划求解工具或函数功能求解方程组可大大提高工作效率、保证求解精度。现以150t冷藏船3500WL为例，说明基于Excel系数ci求解的方法和过程。根据船体型线图，已知条件如表1所示。

表1 型值和端点条件

2 用Excel的规划求解工具求解

2.1 准备计算

为更好地使用Excel求解线性方程组，先进行一阶差商mi·i＋1和线性方程组增广矩阵的计算。

（1）一阶差商的计算

一阶差商mi·i＋1的计算表达式为：mi·i＋1＝利用相关Excel公式求得各一阶差商大小如表2所示。

表2 差商m值的计算

（2）线性方程组增广矩阵的计算

根据三次样条函数系数ci的表达式，利用相关Excel公式求得线性方程组的增广矩阵如表3所示，其中A9：K19单元格区域为系数矩阵，A9：L19单元格区域为增广矩阵。

本例系数行列式的Excel计算公式可表达为“＝MDETERM（A9：K19）”，经计算其值为6.956×1045。根据克莱姆法则，该三次样条函数系数线性方程组有唯一解。

在系数ci的求解表达式（1）、（2）、（3）中，将方程等号右边的常数项移至左边，能使左边多项式的值为零时的ci值即为线性方程组的解。

2.2 “规划求解”命令宏的加载和设置

在默认状态下，Excel的【工具】菜单中无【规划求解】选项。加载方法：单击【工具】菜单的【加载宏】选项，在弹出的【加载宏】对话框中选中【规划求解】选项，单击【确定】按钮。

打开【规划求解选项】对话框，根据求解需要设置【最长运算时间】、【迭代次数】、【精度】、【允许误差】和【收敛度】等选项。

2.3 用规划求解工具求解样条函数系数［3］

如表4、5所示，B21：B31单元格区域用于存放系数的计算结果；C21：C31单元格区域中的各单元格计算公式分别设置为“＝A9＊B21＋B9＊B22－L9”、“＝A10＊B21＋B10＊B22＋C10＊B23－L10”、…和“＝J19＊B30＋K19＊B31－L19”，用于表示方程组左边多项式的值，规划求解前多项式的值如表4所示。

表4 规划求解（1）

单击【工具】菜单中的【规划求解】选项，弹出【规划求解参数】对话框，正确设置【设置目标单元格】、【等于】、【可变单元格】和【约束】等项目，如图1所示，再单击【求解】按钮；在弹出的【规划求解结果】对话框中，选取【保存规划求解结果】，最后单击【确定】按钮。

经规划求解，三次样条函数系数的计算结果如表5中的B21：B31单元格区域所示。注意：目标单元格的值和约束条件的设置必须保证各多项式的值为零。

图1 规划求解参数的设置

表5 规划求解（2）

3 用Excel的函数功能求解

一阶差商mi·i＋1和线性方程组增广矩阵的计算同2.1.1和2.1.2。可用MINVERSE和MMULT函数求系数矩阵的逆阵A－1和方程组的解X＝A－1B。

3.1 用MINVERSE函数求系数矩阵的逆阵

如表6所示，在Excel工作表中选定A33：K43单元格区域，插入函数 MINVERSE，打开MINVERSE函数对话框。

如图2所示，在【函数参数】对话框中的“Array”参数文本框中选取A9：K19单元格区域作为计算逆阵的源数据区域，单击【确定】按钮，将光标定位在编辑栏中所插入函数的结尾处，同时按下组合键“Ctrl＋Shift＋Enter”，用数组公式“｛＝MINVERSE（A9：K19）｝”返回多个计算结果。A33：K43单元格区域显示出逆阵的计算结果，在如表6所示。

表6 系数矩阵逆阵的计算和方程组的求解

图2 “MINVERSE”函数参数的设置

3.2 用MMULT函数求解样条函数系数

如表6所示，在Excel工作表中选定L33：L43单元格区域，插入函数 MMULT，打开MMULT函数对话框。

如图3所示，在【函数参数】对话框中的“Array1”和“Array2”参数文本框中分别选取A33：K43和L9：L19单元格区域作为计算系数ci的源数据区域，单击【确定】按钮，将光标定位在编辑栏中所插入公式的结尾处，同时按下组合键“Ctrl＋Shift＋Enter”，用数组公式“｛＝MMULT（A33：K43，L9：L19）｝”计算出系数ci的计算结果，如表6所示中L33：L43单元格区域所示。

图3 “MMULT”函数参数的设置

讨论：本例亦可利用Excel的 MDETERM函数，根据克莱姆法则［4］进行求解（求解方法和过程略）。

4 结 语

在无相关专业软件的情况下，三次样条函数的求解是一个非常复杂且难以求解的专业问题，用Excel的规划求解工具和函数功能进行计算，不仅能实现复杂问题的简单化处理，大大提高求解效率，同时具有计算模型通用性强、计算过程简明、计算结果准确等优点。

1 徐兆康.船舶建造工艺学［M］.人民交通出版社，2000：50～54.

2 王勇毅.计算机辅助船体建造［M］.人民交通出版社，1995：41～43.

3 谢国锋等.Excel 2000中文版入门提高［M］.清华大学出版社，2000：281～285.

4 同济大学数学教研室.线性代数［M］.高等教育出版社，1991：21.