航速对四筒型基础海洋平台拖航影响的试验分析

丁红岩 ，刘宪庆，张浦阳 ，刁景华，徐飞飞

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；3. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072；4. 海军工程大学天津校区，天津 300450；5. 曹妃甸基础设施投资集团有限公司，唐山 063200)

筒型基础是一种新型的海洋平台基础形式，具有气浮拖航、负压下沉和重复利用性的优势．在浅海区水深不足、大型施工机具不能通过运输船送到指定地点时，筒型基础平台可通过充气浮运用驳船拖到指定地点，然后通过负压进行下沉[1]．同传统打入桩基础相比，可以显著地减少海上施工的时间和费用，并可以重复利用，特别适合我国边际油田的开发．

目前，国内外对于筒型基础的研究主要集中在静稳性的机理和分析上[2-4]，而对波浪作用下筒型基础的运动以及拖航过程中的动稳性还缺乏试验依据和理论分析．拖航中的干舷高度、基础与基础之间的距离、基础的尺寸以及拖航过程中的水深、波浪条件和拖航速度等都是影响筒型基础稳性和耐波性的主要因素．拖航速度过低即拖航动力不足时，平台移位困难，平台受波浪影响，还有可能带动拖轮运动；拖航速度过大时，拖船功率也随之提高，拖航费用增加，过大的拖航速度还会降低平台的稳性和耐波性；因此合理地选择拖航速度是保证拖航经济性和安全性的必然要求．本文采用模型试验的方法，通过在结构上设置压力、拉力和加速度传感器的方法[5-6]，分析了不同拖航速度对四筒型基础海洋平台的稳性以及操纵性的影响．

1 理论分析

1.1 相似理论

模型试验中采用的相似理论公式[7]如下所述．

几何相似常数：

式中：l、b和h分别为模型或原型的长、宽和高；下标m和p分别表示模型和原型．

1.2 平台拖航阻力

平台在拖航时所遭受的阻力包括黏性阻力、兴波阻力和风压阻力[8]．黏性阻力包括形状阻力和摩擦阻力．由于水下部分是由圆柱体组成，形状阻力[9]为

式中：ρ为海水密度，1 .0 25× 1 03kg/m3；A为迎流面积，m2；v为拖航速度，m/s；CD为阻力系数，取决于雷诺数．

摩擦阻力为

式中：S为湿表面积，m2；Cf为摩擦阻力系数，取为0.002 2．

1.3 构件所受波浪力

对于圆柱形构件所受波浪力，按照其尺寸大小的不同采取 2种不同的计算方法．对于小直径构件，当构件的直径 D和波长λ的比值相对很小( /Dλ≤0.15)时，采用半经验半理论的Morison公式；对于大直径构件，采用 MacCamy和 Fuchs提出的绕射理论[10]．

筒型基础结构尺寸相对于波浪来说是小尺寸构件，计算时采用 Morison公式．波浪对结构单筒作用形式如图1所示．

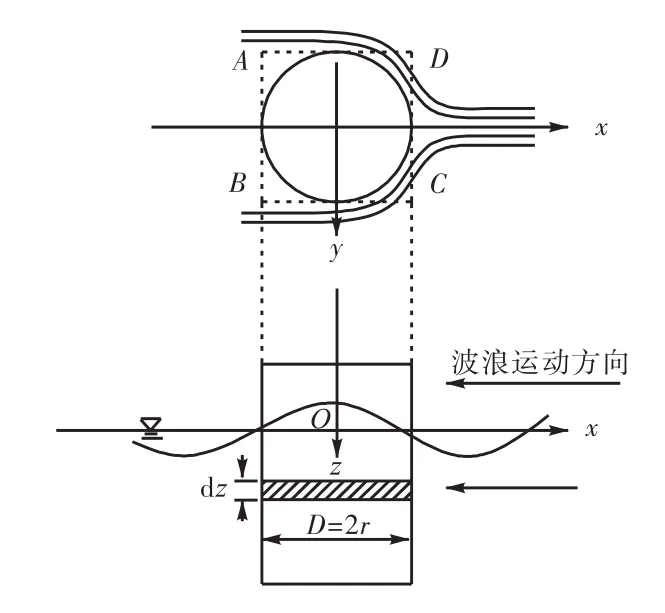
图1 筒体波浪作用示意Fig.1 Schematic diagram of wave action on bucket

当入射波由x轴的正向传来时，在厚度为dz的圆柱形切片上受到的沿x轴方向的波浪扰动力为

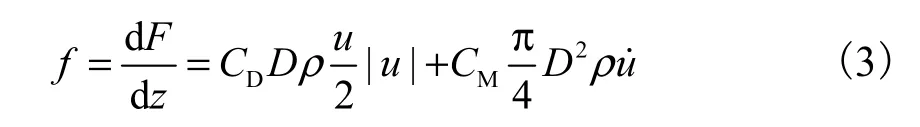
式中：u为切片处未扰动的波浪中流体质点的速度；CM为质量系数，对于圆形剖面的柱体，CM=2 .0，CD= 1 .0[11]．

2 试 验

2.1 试验结构模型

本试验以海军某吸力锚抢修平台为原型，采用1∶20比例模型(原型平台筒直径6.0,m，筒高7.0,m，平台整体高度 22,m)．模型为钢质结构．试验模型按重力和惯性力傅汝德相似定律进行相似比设计，为使平台模型重量分布与平台原型相似，相应地缩小模型重量，试验模型与原型满足总重量、重心位置和惯性矩相似[12]．根据平台重量分布，模型配有一定重量的压载以模拟平台上的设备重量．图 2为波浪控制系统，图3为试验模型，图4为模型入水图．

图2 波浪控制系统Fig.2 Wave control system

图3 1∶20的试验模型Fig.3 Experimental model of 1∶20

图4 拖航模型入水Fig.4 Model of towing in water

2.2 传感器布置

传感器包括拉力传感器、压力传感器(包括气压力和水压力传感器)和加速度传感器．拉力传感器固定于拖车上，作用点处安装有滑轮，拖缆绕过滑轮将结构模型与拉力传感器连接；气压力传感器布置在筒内顶部，水压力传感器布置于筒底；加速度传感器固定于平台顶部中间位置．传感器布置如图 5所示．在拖航过程中，x方向为纵荡方向，y方向为横荡方向，z方向为垂荡方向．

拖航时筒体编号如图6所示，1号筒和3号筒在前，2号筒和4号筒拖航．

2.3 设计组合

试验采用多因素正交设计方法，利用正交组合表来安排试验组合．单个因素水平情况设置为 3个：在吃水深度、倾斜角度、水深等一定的前提下，进行不同拖航速度的静水拖航试验和规则波波高 1,m、波周期为5,s下拖航速度分别为1,kn、2,kn和3,kn拖航试验，以研究筒型基础平台的运动性能．波浪拖航组合如表1所示．

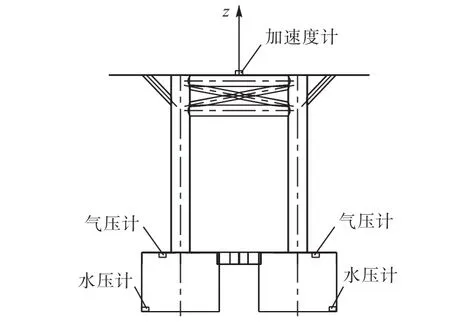
图5 结构立面及传感器布置Fig.5 Vertical structure and layout of sensors

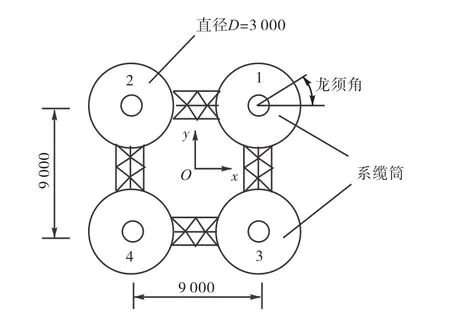
图6 筒体编号Fig.6 Numbers of cylinders

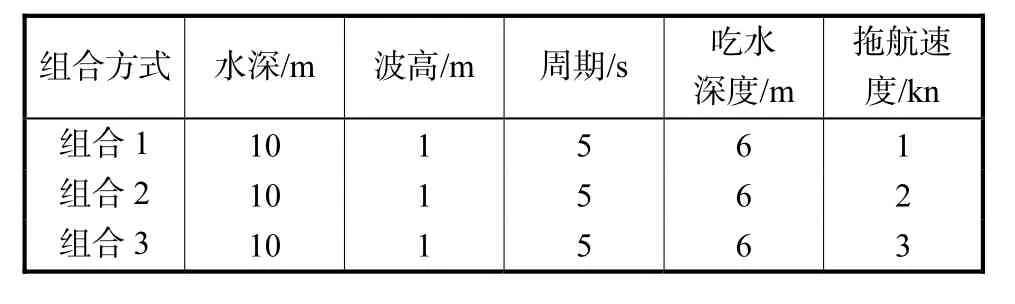
表1 拖航组合Tab.1 Combinations of towing

3 试验测试结果分析

试验中，水压力和气压力采用DS-30型数据采集处理系统采集，加速度通过 DAQ数据采集系统采集．从图 6可以看出，结构前后左右对称且筒底水压力和筒内气压力的变化趋势一致，所以选取系缆筒 1号筒和非系缆筒 2号筒的稳定阶段的筒底水压力数据进行分析比较．以下各图中数据均为由模型测试数据根据相似定律转化后的对应原型结构数据，分析中的峰值都采用测试参数 1/3实测峰值进行分析讨论[13-14]．

试验中采用的规则波波高 1,m、周期 5,s．根据微幅波理论[15]计算所得的波长为 38.87,m，每个筒的直径为 6,m，筒直径和波长的比值为 0.15(属于小尺度构件)，采用Morison公式计算波浪力，计算所得的阻力如表2所示．

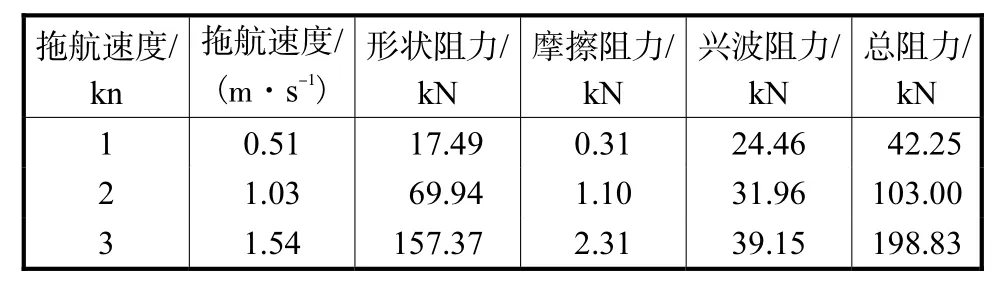
表2 拖航阻力Tab.2 Drags of towing

3.1 静水无波浪拖航分析

目前主要是通过经验公式和模型试验相结合的方法计算筒型基础海洋平台拖航阻力．由于拖航是在室内进行，所以不考虑拖航中风的影响．静水拖航时，在吃水确定的情况下，重力、浮力和水阻力值也可以基本确定(结构的倾斜会导致重力、浮力和阻力力矩产生小幅变动)．根据倾斜力矩和恢复力矩的平衡关系可知，拖缆力有一极限值，即航速存在上限．本平台的无波浪拖航速度上限为3.5 kn．

图7和图 8是无波浪拖航下系缆筒和非系缆筒的水压力变化曲线，图 9为静水拖航的拖缆力变化时程．

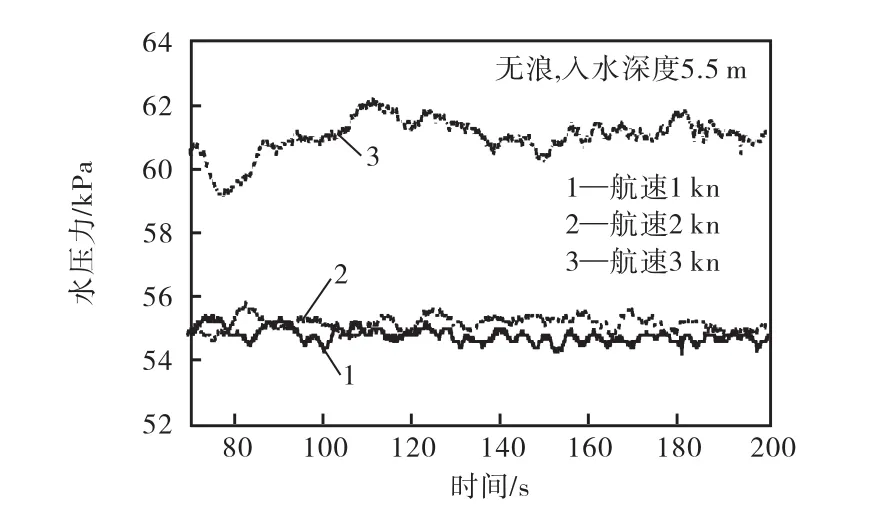
图7 1号筒水压力Fig.7 Water pressure of No.1 bucket

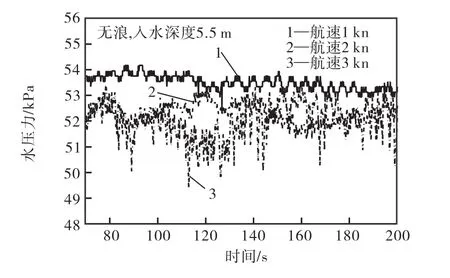
图8 2号筒水压力Fig.8 Water pressure of No.2 bucket

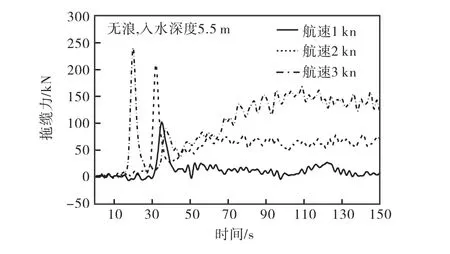
图9 静水拖航的拖缆力变化时程Fig.9 Time history of tension in still water

由图 7和图 8可以看出，在静水拖航的稳定阶段，系缆1号筒的水压力变化稳定且随着拖航速度的增加而增加，非系缆2号筒的水压力变化不稳定且随拖航速度的增加而呈下降趋势．当拖航速度在 2 kn以内时，1号筒的筒底水压力变化不明显，最大幅值变化为 0.61,kPa，而拖航速度在从 2 kn增加到 3 kn的过程中，1号筒底水压力显著增大，最大增幅为8.76,kPa；原因在于随着拖航速度的变大，1号筒沿着拖航方向倾斜，且速度越大 1号筒入水深度也就越大，所以筒底水压力不断变大．2号筒在拖航速度从1 kn增加到2 kn再增加到3 kn的过程中，水压力值不断降低且变化呈现不规则的振荡；原因在于拖航时2号筒也沿着拖航方向倾斜，筒吃水高度降低，水压变小，引起筒底水压力变化的主要原因是由于静水运动中的基础兴起波浪，且拖航速度越大，兴起的波浪越大，处于尾部的 2号筒振荡越明显，兴波阻力也很快增长．

由图 9可以看出，随着拖航速度从1 kn顺次增加到3 kn，最大拖缆力都是发生在脉冲变化部分．这个最大拖揽力是由于开始时结构速度小于拖车、随着拖缆被拉直拖车结构受到拖缆拉力产生的瞬时值，此瞬时值也随着拖航速度的增大而增大；拖航 80,s以后的运动，由于拖缆被拉直，拖缆力处于稳定波动变化状态，产生波动的原因是由于结构的兴波作用，波动的幅度也随着航速增加而增加．

3.2 顺浪拖航分析

图10为顺浪拖航时不同航速下拖缆力的变化情况，图 11为纵荡方向即 x方向的加速度时程曲线．可见拖缆力的变化和拖航速度以及x方向加速度变化相关：拖航速度越快，拖缆力越大；纵荡加速度越大，拖缆力脉冲变化幅度就越大．

从图 10可以看出，拖航速度为 1 kn时，拖缆力变化稳定，结构运动缓慢，波浪推动结构运动．从图11可以看出，拖航速度为1 kn时，纵荡方向的加速度呈现规则的正弦运动，波浪带动基础运动；当拖航速度从1 kn变化到2 kn、从2 kn变化到3 kn时，拖缆力的增幅分别为 848%和 47%，且纵荡加速度最大值分别达到 0.022,m/s2、0.086,m/s2和 0.054,m/s2，幅值先增后降．原因在于波浪对平台拖航时的作用力随着航速与水质点水平振荡速度的相对值而变化：当拖航速度为1 kn时，振荡速度大于航速，波浪对平台的作用力与拖航力方向一致，拖缆承受的力相对较小，波浪推动结构运动；当拖航速度为2 kn时，振荡速度小于航速，波浪对平台的作用力和拖航方向相反；当拖航速度为 3 kn时，虽然波浪的作用力方向仍然和拖航方向相反，但是增加的幅度降低，所以纵荡加速度呈先增加后降低的趋势．

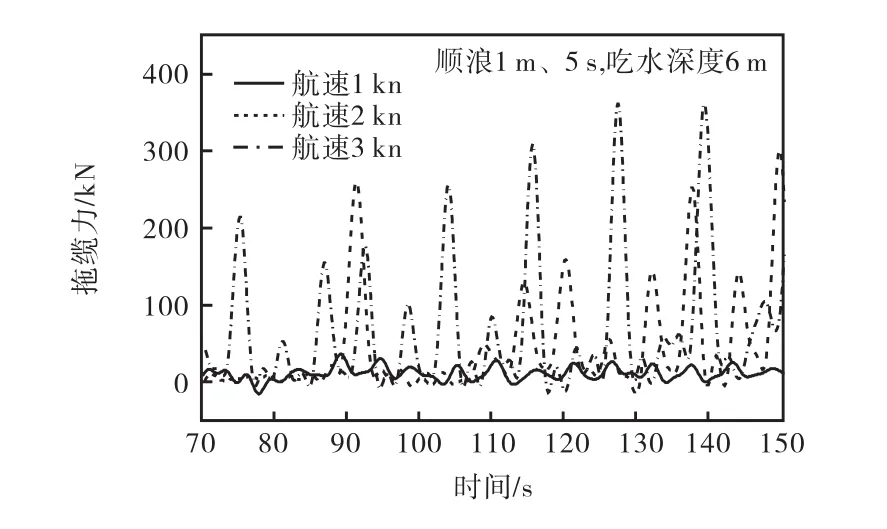
图10 拖缆力时程(顺浪)Fig.10 Time history of tension(following wave)

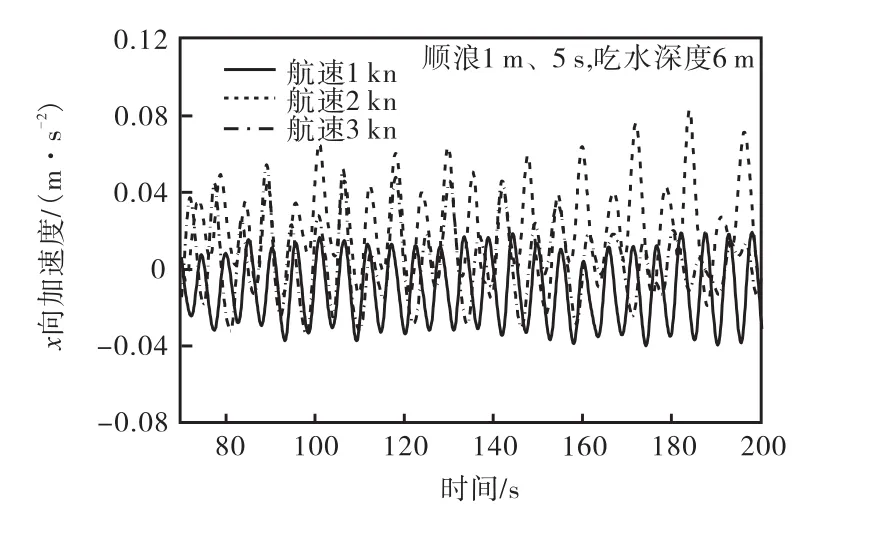
图11 x方向加速度时程(顺浪)Fig.11 Time history of acceleration in x direction(following wave)

图12 和图13为通过加速度传感器测得的顺浪、不同拖航速度下横荡和垂荡加速度时程变化．从图12可以看出，在拖航速度为1 kn、2 kn和3 kn时，在拖航横荡方向的加速度绝对值幅值分别为0.037, m/s2、0.068,m/s2和 0.040,m/s2，加速度先增后减．从图 13可以看出，拖航速度为1 kn时，垂荡加速度幅值和振荡幅度明显小于拖航速度为2 kn和3 kn时的幅值和振荡幅度，且拖航速度从1 kn顺次变化到3 kn时，加速度幅值也是先增后减，增幅为146%，降幅为17.4%．这是因为结构产生横荡与水质点水平振荡速度和拖航速度相对值有关：振荡速度大于航速时，相对值越大，横荡越大；振荡速度小于航速时，相对值越大，横荡越小．拖航速度为 1 kn时，振荡速度大于航速，航速接近于振荡速度，横荡运动相对较小；拖航速度为2 kn时，振荡速度小于航速，幅度大于振荡速度和航速相对值较大时的 3 kn拖航．结构垂荡是由于波浪变化引起的，随着航速的增加而增加；但是当航速达到一定限制时，增加的幅度将变得平缓．

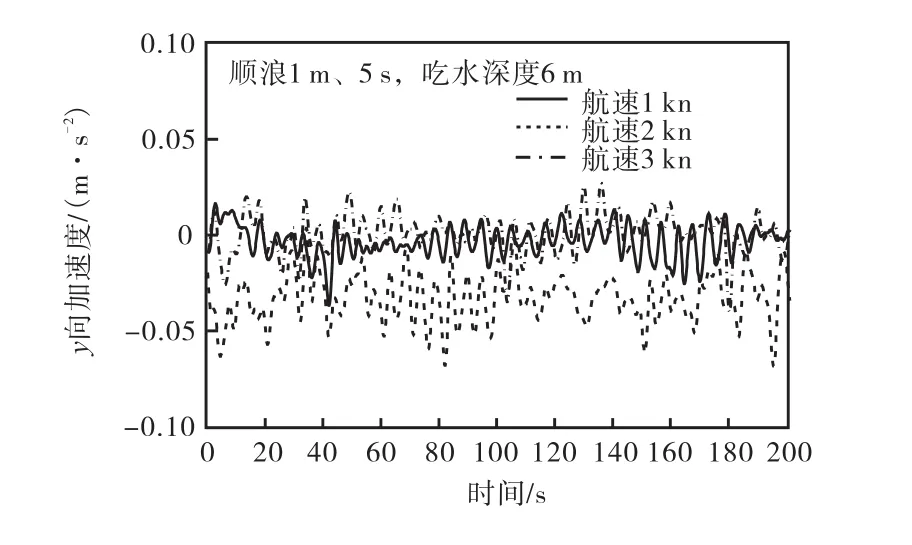
图12 y方向加速度时程(顺浪)Fig.12 Time history of acceleration in y direction(following wave)

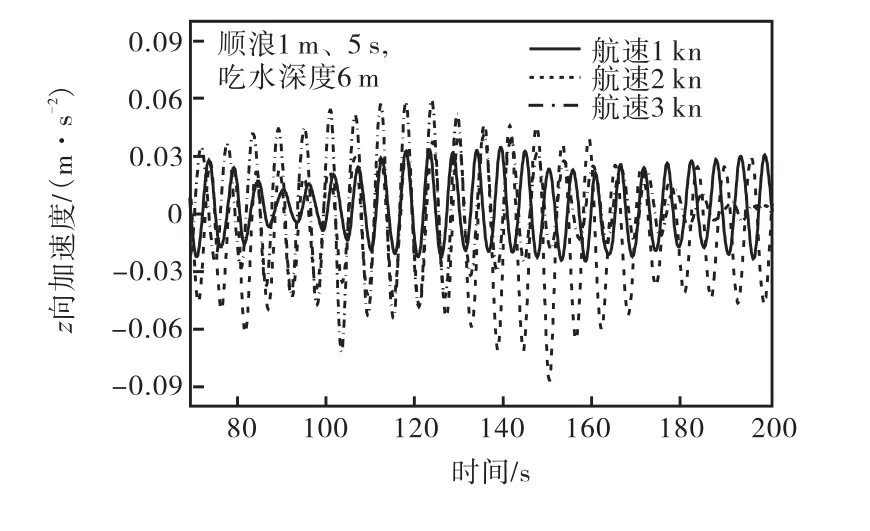
图13 z方向加速度时程(顺浪)Fig.13 Time history of acceleration in z direction(following wave)

3.3 逆浪拖航分析

图14 和图15为逆浪、不同航速下拖航的拖缆力和纵荡加速度时程变化曲线．可以看出，拖缆力随着拖航速度的增加而增加；在拖航速度小于2 kn时，拖缆力的脉冲幅度相对较小；在拖航速度大于2 kn时，拖缆力脉冲幅度较大；航速从1 kn增加到2 kn、从2 kn增加到 3 kn时，拖缆力增幅分别为 563%和 29%．原因在于逆浪拖航时，当拖航速度较小时，水质点水平振荡速度大于航速，拖航过程中的摩擦阻力和形状阻力相对较小，作用在结构上的力主要是波浪力；当拖航速度较大即大于振荡速度时，拖航过程中的形状阻力增加．从图 15还可以看出，纵荡加速度随着拖航速度的增大其幅度和幅值都呈增加的趋势，拖缆力脉冲的幅度和幅值都随着纵荡加速度的增加而增加．

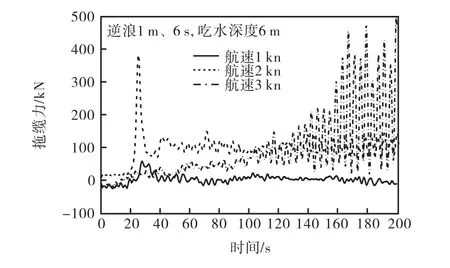
图14 拖缆力时程(逆浪)Fig.14 Time history of tension(head wave)

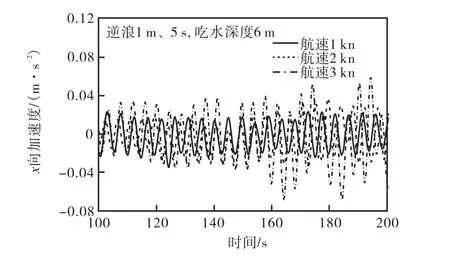
图15 x方向加速度时程(逆浪)Fig.15 Time history of acceleration in x direction(head wave)

图16和图 17为不同航速下逆浪拖航横荡和垂荡加速度变化曲线．从图 16可以看出，逆浪拖航下，横荡加速度随着航速的增加而降低，在拖航的稳定阶段横荡也是稳定的，横荡加速度仅有小幅度的波动．从图17可以看出，结构垂荡运动在航速为1,kn、2,kn和 3,kn的幅值降低，分别为 0.075,m/s2、0.057,m/s2和 0.042,m/s2，垂荡运动的幅度也随着航速增加而降低．

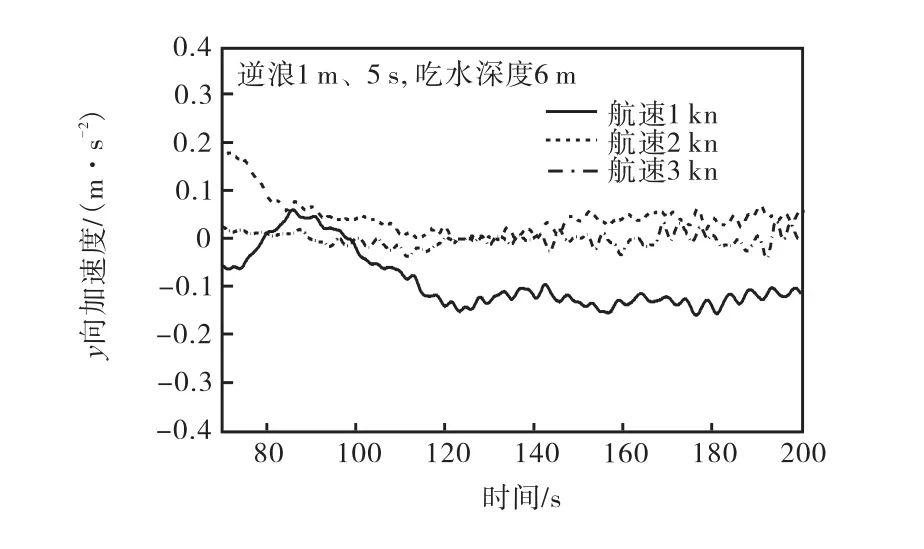
图16 y方向加速度时程(逆浪)Fig.16 Time history of acceleration in y direction(head wave)

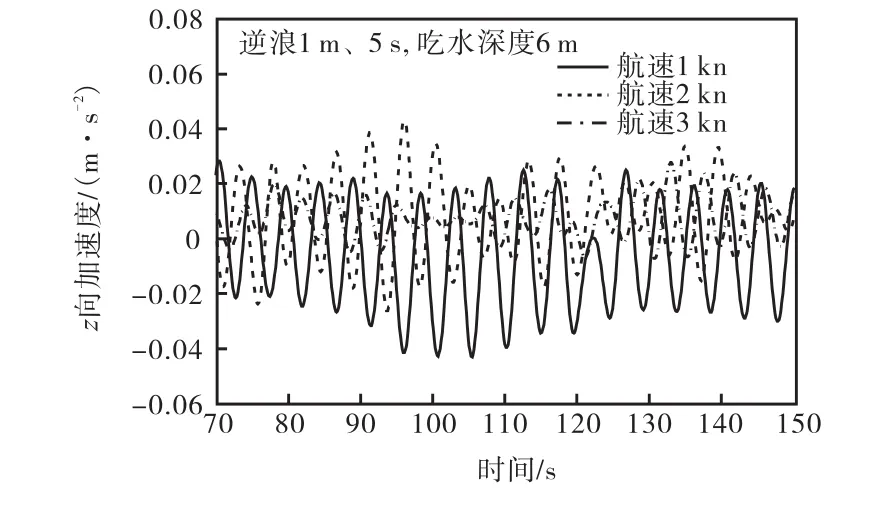
图17 z方向加速度时程(逆浪)Fig.17 Time history of acceleration in z direction(head wave)

4 结 论

(1) 筒型基础在确定的条件下静水拖航时，拖航速度存在一个上限值，该平台的最大拖航速度为 3.5 kn．实际施工中，筒型基础平台必须进行静水拖航试验来确定此上限值．

(2) 拖缆力的变化主要受航速和水质点水平振荡速度的相对值、纵荡加速度的影响．航速小于振荡速度时，拖缆力较小；航速大于振荡速度时，振荡速度与航速相差越大，拖缆力越大，但是增加的幅度随相对值的增加而降低．

(3) 筒型基础的纵荡运动随着航速的增加而增加，拖缆力脉冲的幅度也随之增大．

(4) 随着航速的增加，顺浪拖航时垂荡运动增大，逆浪拖航时垂荡加速度降低，平台拖航时遇到大浪情况下，降低拖航速度是保证稳性行之有效的途径．

(5) 为了满足结构快速性、耐波性以及经济性的要求，在其他拖航条件一定的情况下，建议该结构的拖航速度为2 kn．

［1］ Ding Hongyan，Zhang Puyang. Estimation of heights of soil plug inside bucket foundations during suction penetration by deformable discrete element modeling[J].Transactions of Tianjin University，2007，13(4)：308-312.

［2］ 别社安，时忠民，王翎羽. 气浮结构的静浮态分析[J]. 中国港湾建设，2000(6)：18-23.Bie She’an，Shi Zhongmin，Wang Lingyu. Floating state analysis of air float structure[J]. China Harbour Engineering，2000(6)：18-23(in Chinese).

［3］ 别社安，时忠民，王翎羽. 气浮结构的小倾角浮稳性分析[J]. 中国港湾建设，2001(1)：31-36.Bie She’an，Shi Zhongmin，Wang Lingyu. Stability analysis of air float structures with small roll angle [J].China Harbour Engineering，2001(1)：31-36(in Chinese).

［4］ 别社安，时忠民，王翎羽. 气浮结构的运动特性研究[J]. 中国港湾建设，2001(2)：18-21，25.Bie She’an，Shi Zhongmin，Wang Lingyu. Study on kinetic properties of air float structures[J]. China Harbour Engineering，2001(2)：18-21，25(in Chinese).

［5］ Ding Hongyan，Qi Lan，Xu Jizu. The bucket foundation platforms installed in shallow and ice drifting area[J]. Journal of Cold Regions Engineering，2001，15(4)：211-218.

［6］ Hua Jianbo. Assessment of the course-keeping ability of a fast ship in following waves[J]. Journal of Ship Mechanics，2004，8(6)：1-12.

［7］ 李忠献. 工程结构试验理论与技术[M]. 天津：天津大学出版社，2004.Li Zhongxian. Test Technology and Theory of Engineering Structures[M]. Tianjin：Tianjin University Press，2004(in Chinese).

［8］ 姜次平，邵世明. 船舶阻力[M]. 上海：上海交通大学出版社，1985：3-63.Jiang Ciping，Shao Shiming. Ship Resistance[M].Shanghai： Shanghai Jiao Tong University Press，1985：3-63(in Chinese).

［9］ 中国船级社. 移动式海洋平台入级规范[M]. 北京：人民交通出版社，2005：76-86.China Classification Society. Rules and Regulations for Mobile Offshore Platform[M]. Beijing：China Communications Press，2005：76-86(in Chinese).

［10］ 李玉成，滕 斌. 波浪对海上建筑物的作用[M]. 北京：海洋出版社，2002：250-255.Li Yucheng，Teng Bin. The Effects of Waves on Offshore Structures[M]. Beijing：China Ocean Press，2002：250-255(in Chinese).

［11］ 苏兴翘. 船舶与海洋构筑物动力学[M]. 天津：天津大学出版社，1992：102-105.Su Xingqiao. Dynamics of Ship and Marine Installations[M]. Tianjin：Tianjin University Press，1992：102-105(in Chinese).

［12］ 夏国泽. 船舶流体力学[M]. 武汉：华中科技大学出版社，2003：160-170.Xia Guoze. Ship Hydrodynamics[M]. Wuhan：Huazhong University of Science and Technology Press，2003：160-170(in Chinese).

［13］ Clauss G F，Katja Stulz. Time-domain analysis of floating bodies with forward speed[J]. Journal of Offshore Mechanics and Arctic Engineering，2002，124(2)：66-73.

［14］ Irvine M J. Towing Tank Tests for Surface Combatant for Coupled Pitch and Heave and Free Roll Decay Motions[M]. Iowa：The University of Iowa Press，2004：89-170.

［15］ 李远林. 近海结构水动力学[M]. 广州：华南理工大学出版社，1999：92-103.Li Yuanlin. Dynamics of Offshore Structures[M]. Guangzhou：South China University of Technology Press，1999：92-103(in Chinese).