全相位双正交五株形滤波器组的设计与应用

侯正信，郭岩松，，杨爱萍，何宇清

(天津大学电子信息工程学院，天津 300072)

两通道五株形滤波器组(quincunx filter bank，QFB)是图像多尺度几何表示中最为关键的滤波器组，是构成方向滤波器组(directional filter banks，DFB)[1-2]和 Contourlet变换[3-4]等复杂系统最基本的结构单元，具有重要的研究价值．现有的 QFB设计方法种类很多，诸如 Bernstein多项式方法[5-6]、方向奇异值分解(singular value decomposition，SVD)法[7]和 McClellan变换法[8-9]等．Bernstein多项式方法将二维对称频率响应转换到一个新的变换域，使用二维Bernstein多项式来近似，结果滤波器的通带和阻带区域比较平坦；但是由于 Bernstein多项式收敛速度太慢，故过渡带较宽．方向奇异值分解法把通用不可分离符号和SVD结合起来设计符合钻石形半带条件的二维变换核，用于视频抽样结构和设计二维不可分离完全重建滤波器组，侧重于研究变换核的设计．McClellan变换法是一种应用广泛的二维零相位有限冲激响应(finite impulse response，FIR)滤波器设计方法，蕴含着由一维频率映射为二维频率的基本思想．

文献[10]提出了使用二维递归对称半平面全通数字滤波器和并行结构构造两通道五株形正交镜像滤波器组(quincunx quadrature mirror filter bank，QQMFB)的新颖方法，其分析和综合滤波器具有二维双重互补半带(doubly complementary half band，DC-HB)特性，满足无混叠赝像的频率约束条件，但这种 QQMFB只能提供无幅度失真的近似线性相位响应．总之，各种 QFBs设计方法都各有利弊，很难找到一种一成不变的方法，通常需要根据具体情况做出权衡．

对于 FIR完全重建滤波器组而言，线性相位和正交镜像是一对不可调和的矛盾，在图像和视频处理中，相位的畸变极易引起图像的失真，对视觉效果造成不良影响．本文提出一种折中方案，在保证线性相位和完全重建前提下，构造一种新的全相位钻石形变换核函数，使用改进的准 QMF模型[11]设计一类新的QFB，称为全相位双正交五株形滤波器组(all phase biorthogonal quincunx filter bank，apbQFB)．

1 两通道五株形滤波器组(QFB)

两通道 QFB的系统框图如图 1所示．图中，H0( z1, z2)和 H1( z1, z2)分别表示低通和高通分析滤波器，G0( z1, z2)和G1( z1, z2)分别表示低通和高通综合滤波器，符号↓Q和↑Q分别表示五株形抽取和内插．钻石形和扇形 QFB是方向滤波器组和图像多尺度分析中最常用的两种 QFB，如图 2所示．扇形QFB的各个滤波器可由钻石形QFB的各个对应滤波器在频域中沿着ω1轴或者ω2轴调制π得到；反之亦然．

图1 两通道五株形滤波器组(QFB)Fig.1 Two-channel quincunx filter bank(QFB)

对信号 x ( n1, n2)(z变换为 X ( z1, z2))，先Q抽取再内插等价于调制一个 q ( n1, n2)函数，即 q ( n1, n2)⋅x( n1, n2)．其中

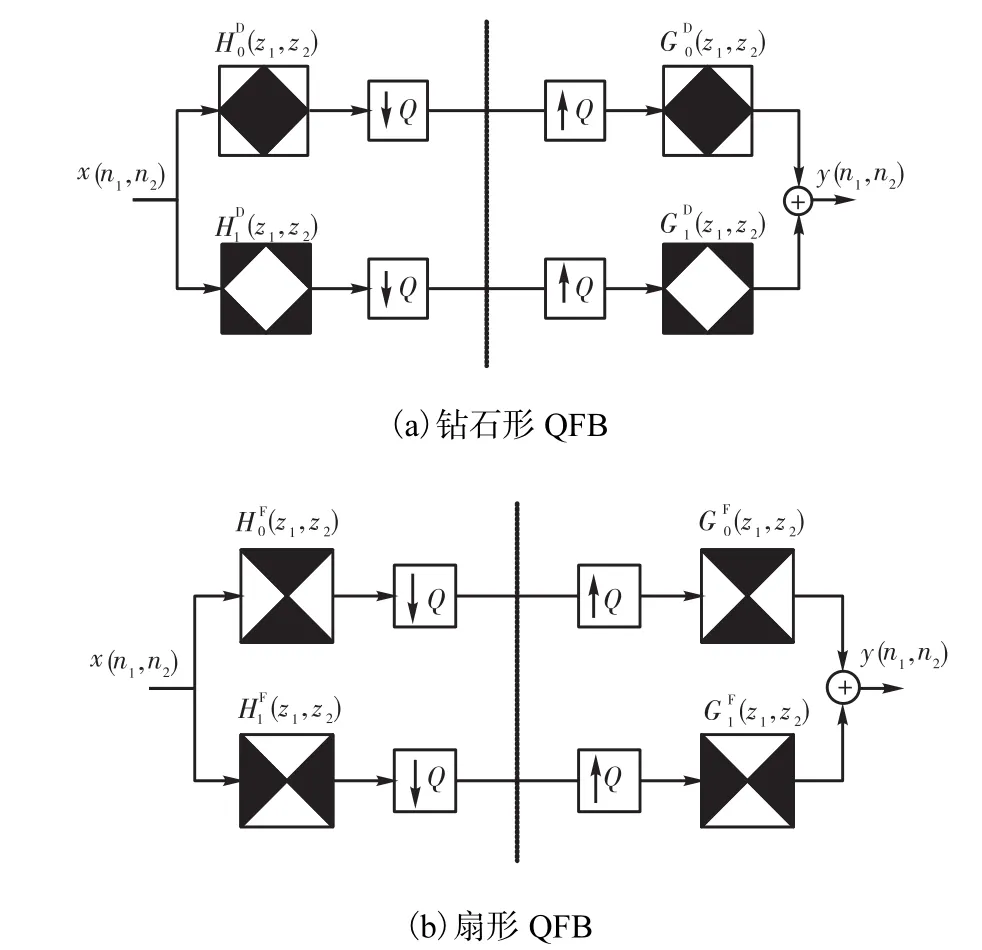
图2 钻石形和扇形QFB(黑色区域表示理想通带)Fig.2 Diamond and fan shape QFB(black region represents ideal passband)

即在n1+ n2= e ven时采样子栅格上的点保留不变，在n1+ n2= o dd时采样子栅格上的点置零．X ( z1, z2)变换为因此，QFB 的输入/输出关系可表示为

式中：与 X ( z1, z2)相关的第 1项表示原始信号分量；与X(− z1, − z2)相关的第2项表示信号混叠分量．当且仅当满足

时，QFB可以完全重建．式(3)称为双正交关系．当QFB中各个滤波器均为实用的 FIR滤波器时，低通滤波器与高通滤波器必须满足式(4)关系才能去除混叠分量，实现完全重建，即

式中 K1+ K2= o dd ，本文中如不做特殊说明，一般取K1= 0，K2=1．去除混叠分量后的 QFB为一个线性时不变系统，即 Y ( z1, z2) = T( z1, z2) X( z1, z2)．线性时不变转移函数 T ( z1, z2)为

其中乘积滤波器 D ( z1, z2)定义为

式(7)实际上蕴含功率互补关系，与半带滤波器证明相似[12]，等价于

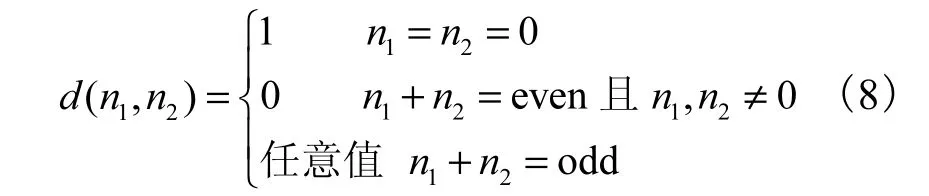
理论上，乘积滤波器 D ( z1, z2)可以在约束条件式(7)下进行设计，通过因式分解得到低通滤波器H0( z1, z2)和G0( z1, z2)．但由于缺乏二维多项式因式分解的基本定理和法则[13]，通常避免直接分解二维多项式．变量变换法[11]将二维多项式因式分解降维为一维问题来处理，下文简要介绍变量变换法．

2 变量变换法与乘积滤波器

定义变量变换

容易证明 m ( n1, n2)必须满足条件

Z = M ( z1, z2)隐含可将二维乘积滤波器 D ( z1, z2)转化为一维多项式 DT(Z)，称 DT(Z)为一维乘积滤波器．虽然并不是对于所有 D ( z1, z2)都存在这种变量变换，但实际应用中通常考虑变换可能存在的情况．

利用变量变换式(9)，约束条件式(7)转化为另外一种约束，即

下面给出关于变量变换的定理 1，具体证明可参考文献[11]．则乘积滤波器

定理 1足完全重建约束条件式(7)．

利用定理 1，一维乘积滤波器T()D Z可分解成一阶因子乘积，即

式中C为常数．若将一阶因子分别分配给 HT(Z)和GT(Z ) ，即 DT( Z ) = HT( Z) GT(Z)，再由变量变换Z=M( z1, z2)可得低通分析滤波器 H0(z1, z2) = HT( M ( z1,z2))和低通综合滤波器 G0( z1, z2) = GT( M ( z1, z2))．为得到实系数滤波器，复共轭因子对(Z−c)和(Z−c*)必须分配给同一滤波器．一阶因子(Z −al)可理解为基本滤波器(M ( z1,z2) − al)，将其级联形成分析滤波器H0和 G0．基本滤波器由变换函数 M ( z1, z2)和额外因子−al组成．

3 全相位双正交五株形滤波器组设计步骤

若基于全相位方向滤波器(all phase directional filter，APDF)设计出性能优良的变量变换核函数，再利用满足约束条件式(11)的双正交关系生成 QFB，则称为全相位双正交五株形滤波器组(apbQFB)，其可由以下2个主要步骤完成设计．

(1) 设计满足约束条件式(10)的全相位变换核函数 m ( n1, n2)(即 M ( z1, z2))．

(2) 寻找满足约束条件式(11)的一维乘积滤波器 DT(Z)，因式分解产生 HT(Z)和 GT(Z)，并进行变量变换 Z = M ( z1, z2)，得到 H0( z1, z2) = HT( M ( z1, z2))，G0( z1, z2) = GT( M ( z1, z2))．

步骤 1说明如何生成全相位变换核函数是设计的关键，第4节将会详细讨论．步骤2由一维乘积滤波器 DT(Z)分解得到的 HT(Z)和 GT(Z)，只是一些简单的一维滤波器．但 QFB中各滤波器的性能并不仅由一维滤波器决定，还与全相位变换核函数 M ( z1, z2)密切有关，两者相互结合才能生成性能良好的apbQFB．文献[11]使用 Lagrange半带滤波器[14]及其修改形式分解求得 HT(Z)和 GT(Z)，本文采用其中一种改进的完全重构准QMF模型，即

4 基于一维全相位半带数字滤波器生成全相位变换核函数

如图 3(a)所示(黑色为通带，白色为阻带)，考虑理想钻石形通带区域滤波器的频率响应

为使Q抽取/内插后仍然为单位增益，通带区域值等于2．由逆傅里叶变换求得单位脉冲响应

式中sinc() sinv v v= ．式(15)为 2个sinc函数沿 2个对角线的乘积．除原点外，脉冲响应满足式(10)．若将中原点删除，则准确满足式(10)．由于时域中删除原点上的单位脉冲响应相当于频域平面中向下平移1个单位，即

虽然频率响应范围为1−～1，但是钻石形频率响应的形状依然保持不变，这实质为变换核函数的理想频率响应利用窗函数截断删除原点值的无限长脉冲响应可得变换核函数

式中1()w n可为任意一维非因果窗，如凯塞窗、汉明窗、切比雪夫窗等．但式(18)并非二维窗函数的唯一可能形式，该窗函数在频域中沿着 45°和 135°方向产生均匀的“窗函数效应”，滤波器具有钻石形频率支撑区域．由于窗函数的截断产生误差，的实际频率响应只能近似等于式(16)．窗函数既可决定变换核函数的掩模大小，亦可调整控制的频响特性，例如频率滚降和幅度波纹等．结合式(18)二维窗函数和式(15)理想脉冲响应可表示为

其中

实际为一个半带滤波器，所以1()m n的设计与加窗半带滤波器的设计相似．通过简单数学变换，式(19)的z变换可表示为

其频域形式为

图3 理想钻石形频率支撑区与全相位变换核函数Fig.3 Ideal diamond shape frequency support region and all phase transform kernal function

目前，一维FIR半带滤波器的设计方法种类很多，主要有Lagrange半带滤波器[14]和Bernstein多项式展开法[15]等．文献[16]叙述了一种基于离散傅里叶变换(discrete Fourier transform，DFT)域的全相位半带滤波器(apHF)，通带和阻带波纹较小，在过渡带附近频率响应没有过冲现象，具有一定的优良性质．本文采用另外一类基于离散傅里叶逆变换(inverse discrete Fourier transform，IDFT)域的全相位半带数字滤波器，其设计更加灵活，选用适当的窗函数可极大地减小吉布斯效应，显著地改善频率特性．基于IDCT域的一维全相位半带滤波器设计步骤如下所述．

(1) 根据对截止频率精度和实现复杂度的要求，适当地选择基于 IDCT域的 apHF的长度 4M K= −1，即恰当地选择K值．

(4) 求出基于 IDCT域加窗 APDF的单位脉冲响应

(3) 选择适当的窗函数即

式中 fN=[f ( 0),f ( 1), … ,f( N −1)]为 D CT ( FN)，即频率响应向量 FN的余弦谱．归一化 pN(n)得全相位半带数字滤波器(apHF) pHB(n)( n =− ( 2 K − 1 ),… ,0 ,…,2 K − 1)满足

图4 apbQFB Ⅰ各滤波器的幅频响应Fig.4 Amplitude-frequency response of apbQFB I filters

(5)由式(21)可知 m1( n) = 2 pHB(n) − δ (n)，利用式(19)或式(22)可求得全相位变换核函数 m ( n1, n2)．

5 设计实例

全相位变换核 ma(n1, n2)如下述式(28)所示，其幅频响应如图 3(b)所示．分析滤波器和综合滤波器 G0( z1, z2)、的坐标范围如表 1所示(式(4)中取 K1= 0 ，K2=1)，各滤波器的幅频响应如图4所示．

表1 apbQFBⅠ的各个滤波器的坐标范围Tab.1 Coordinates range of apbQFBⅠfilters

6 全相位Contourlet及其应用

利用 apbQFBⅠ的方法构造 DFB[2]，并替换原Contourlet变换[3-4]中的DFB，生成新的Contourlet变换，称为全相位Contourlet(apContourlet)．本节以原Contourlet和CDF9 7小波作为对比，研究apContourlet在非线性估计和图像降噪方面的客观性能和主观视觉效果．

6.1 非线性估计

非线性估计(nonlinear approximation，NLA)是衡量图像变换的能量聚集能力的一种重要手段．保留幅值最大的 N个分解系数重构图像并计算峰值信噪比(peak signal-to-noise ratio，PSNR)，当保留相同数目的系数时，PSNR值越大说明分解的稀疏性越好，更逼近原图像．分别利用apContourlet、原Contourlet工具箱[18]和9 7小波对纹理和细节丰富的Barbara图像进行非线性估计．两种Contourlet变换(apContourlet和原Contourlet)采用与9 7小波联合的5层混合结构进行分解．其中，第 1层 DFB方向数为 25，第 2层DFB方向数为 24，然后再进行 3层9 7小波分解．原Barbara灰度图像的像素总数为512× 512=262144，分解后系数总数变为 2 62144 × ( 1 + 0 .25 + 0 .252)=3 44 064，非线性估计时保留系数 a的数目利用原图像像素总数的百分比来表示．

两种 Contourlet变换和CDF9 7小波非线性估计的 PSNR比较如表 2所示．为更清晰直观，画出PSNR随系数保留百分比的变化曲线，如图 5所示．由表 2和图 5可知：apContourlet非线性估计性能明显优于原 Contourlet工具箱，大约提高 1～2,dB；而9 7小波的非线性估计性能则随着保留系数百分比的增加依次超越原Contourlet和apContourlet.

表2 apContourlet、原Contourlet和CDF9/7小波非线性估计的PSNR比较Tab.2 Comparision of nonlinear estimation PSNR for apContourlet，original Contourlet and CDF9/7 wavelet

图5 非线性估计PSNR值随系数保留百分比的变化曲线Fig.5 Nonlinear estimation PSNR vs coefficients preservation percentage

6.2 图像降噪

对尺寸为512× 512的测试图像Lena和Barbara进行降噪实验，其中前者低频平滑信息较多，而后者纹理和细节丰富．采用与9 7小波联合的 5层混合结构(第 1、2、3层 2种 Contourlet变换的 DFB方向数分别为 25、24和 24，然后进行2层9 7小波变换)．在不同加性高斯白噪声水平下，利用3倍标准方差的简单阈值降低两幅测试图像的噪声．表 3为 Lena和Barbara图像利用CDF9 7小波、原 Contourlet和apContourlet降噪的PSNR值，图6和图7分别给出了在图像噪声水平为 15.90 dB时降噪的局部主观效果，其中对于 Barbara图像的降噪效果的改善明显优于 Lena图像．数值实验结果和主观视觉效果都表明：采用 apbQFB实现的 apContourlet变换的 PSNR值略高于原Contourlet．

图6 Lena图像噪声水平为15.90,dB时降噪的局部主观效果Fig.6 Local subjective effects of Lena image denoising for noise level 15.90,dB

图7 Barbara图像噪声水平为15.90,dB时降噪的局部主观效果Fig.7 Local subjective effects of Barbara image denoising for noise level 15.90,dB

表3 在不同噪声水平下降噪的PSNR比较Tab.3 Comparision of denoise PSNR under various noise levels

7 结 语

本文使用构造的全相位钻石形变换核函数和改进的准 QMF模型设计了一类新的 QFBs，其能够保证线性相位和完全重建条件，称为全相位双正交五株形滤波器组(apbQFB)．重点研究了全相位钻石形变换核函数这个关键点，给出了基于一维IDCT域全相位半带数字滤波器的生成方法．利用apbQFB构造原Contourlet变换中的 DFB，生成一种新的 Contourlet变换，即全相位 Contourlet(apContourlet)，并研究其在非线性估计和图像降噪方面的应用．以原Contourlet变换和CDF 9/7小波作为比较对象，研究了 apContourlet变换在非线性估计和图像降噪方面的应用．实验结果表明：在相同的分解层数下，apContourlet的非线性估计和降噪性能均优于原Contourlet，全相位 Contourlet变换的初步性能验证结果亦说明 apbQFB设计方法具有较好的通用性和优越性．

［1］ Bamberger R H，Smith M J T. A filter bank for the directional decomposition of images：Theory and design[J].IEEE Transactions on Signal Processing，1992，40(4)：882-893.

［2］ Do M N. Directional Multiresolution Image Presentation[D]. Swiss：Department of Electrical and Computer Engineering，Swiss Federal Institute，2001.

［3］ Do M N，Vetterli M. Contourlets：A new directional multiresolution image representation[C]//Proceedings of Conference Record of the Asilomar Conference on Signals，Systems and Computers. Pacific Grove，CA，USA，2002：497-501.

［4］ Do M N，Vetterli M. The contourlet transform：An efficient directional multiresolution image representation[J]. IEEE Transactions on Image Processing，2005，14(12)：2091-2106.

［5］ Pei S C，Wang P H. Design of arbitrary cutoff 2-D diamond-shaped FIR filters using the Bernstein polynomial[J]. IEEE Signal Processing Letters，2000，7(11)：310-313.

［6］ Cooklev T，Yoshida T，Nishihara A. Maximally flat half-band diamond-shaped FIR filters using the Bernstein polynomial [J]. IEEE Transactions on Circuits and SystemsⅡ：Analog and Digital Signal Processing，1993，40(11)：749-751.

［7］ Tay D B H. Directional SVD：A new technique for designing 2-D diamond halfband filters and filter banks[C]//Proceedings of International Conference on Digital Signal Processing. Santorini，Greece，1997：455-458.［8］ Song Y S，Lee Y H. Formulas for McClellan transform parameters in designing 2-D zero-phase FIR fan filters[J]. IEEE Signal Processing Letters，1996，3(11)：291-293.

［9］ Shpairo J M. Adaptive McClellan transformations for quincunx filter banks[J]. IEEE Transactions on Signal Processing，1994，42(3)：642-648.

［10］ Lee J H，Yang Y H. Two-channel quincunx QMF banks using two-dimensional digital allpass filters[J]. IEEE Transactions on Circuits and SystemsⅠ：Regular Papers，2009，56(12)：2644-2654.

［11］ Tay D B H，Kingsbury N G. Flexible design of multidimensional perfect reconstruction FIR 2-band filters using transformations of variables[J]. IEEE Transactions on Image Processing，1993，2(4)：466-480.

［12］ 胡广书. 现代信号处理教程[M]. 北京：清华大学出版社，2004.Hu Guangshu. Modern Signal Processing Tutorial[M].Beijing：Tsinghua University Press，2004(in Chinese).

［13］ Lim J S. Two-Dimensional Signal and Image Processing[M]. Englewood Cliffs，NJ：Prentice-Hall，1990.

［14］ Ansari R，Guillemot C，Kaiser J F. Wavelet construction using Lagrange halfband filters[J]. IEEE Transactions on Circuits and Systems，1991，38(9)：1116-1118.

［15］ Zarowski C J. Comments on regular half-band filter design via Bernstein polynomial expansions[C]// Proceedings of IEEE Pacific RIM Conference on Communications，Computers，and Signal Processing. Victoria，BC，Canada，1997：477-480.

［16］ 徐妮妮，侯正信．全相位半带滤波器及其应用[J]. 天津大学学报，2005，38(3)：206-211.Xu Nini，Hou Zhengxin. All phase half band filter and its application[J]．Journal of Tianjin University，2005，38(3)：206-211(in Chinese)．

［17］ 侯正信，赵黎丽. 基于 IDCT域的加窗全相位数字滤波器[J]. 天津大学学报，2006，39(12)：1499-1503.Hou Zhengxin，Zhao Lili．Windowed all phase digital filter based on IDCT[J]. Journal of Tianjin University，2006，39(12)：1499-1503(in China).

［18］ Do M N. Contourlet Toolbox[EB/OL]. http：//www. ifp.illinois. edu/～minhdo/software/，2007-04-01.