基于区间有限元的吊梁非概率可靠性研究及敏感性分析

韩志杰，王璋奇

(华北电力大学 能源动力与机械工程学院，河北 保定，071003)

目前，吊梁的设计需考虑抗弯能力及整体稳定性。而在工程设计中，为了保证吊梁的可靠性，一般给定塑性发展系数和整体稳定系数等确定性的指标来调整，而这些指标一般通过查表或者经验来确定，虽然长期实践证明这种方法是一种有效的工程应用方法，但由于吊梁在设计制造中，存在着大量的不可测或不可控因素，使吊梁设计参数具有不确定性或不可控性，导致设计与分析结果难以反映工程实际，从而影响产品设计质量，因此，需要在准确描述设计参数不确定性的基础上研究吊梁可靠性。以不确定性为基础来分析结构的方法主要有：随机有限元法[1-2]、模糊有限元法[3]和区间有限元法[4-5]。前两种方法是解决不确定问题常用方法，它们是通过用随机概率理论或模糊理论结合确定性有限元来分析问题，但是它们在求解时，需要确定不确定性参数的概率密度或隶属函数，这需要大量的样本点，要获取样本点最直接的方法是试验测定，对于吊梁这种大型机械结构很难实现，因此使不确定性参数的概率密度函数难以确定，往往通过人为方式取舍；文献[6-7]中分别把随机有限元和模糊有限元结合可靠性对机械结构做了分析，建立了不确定结构可靠性解决方案，由于对具有较少样本点的结构不确定性描述不确切，致使计算结果与实际存在偏差。而区间有限元分析方法在针对统计信息不足以描述不确定参数的概率分布或隶属函数时，仅需提供不确定参数的区间范围即可获得结构响应的区间范围。因此，本文作者在对吊梁受力模型分析的基础上，利用区间分析来描述吊梁设计参数的不确定性，结合区间有限元法建立结构有限元控制方程，并利用一阶泰勒展开方法求解此方程，获得吊梁结构响应区间，并引入非概率可靠性设计思想，分析吊梁的可靠性验算，建立了各失效模式下的极限状态函数，根据吊梁结构响应区间确定了其可靠性指标，来描述结构的可靠性程度，最后对区间敏感性进行定义，分析设计参数在区间内变化对结构响应的敏感程度，以便为吊梁的设计提供参考依据。

1 吊梁模型的建立与分析

吊梁的主体结构为多个等厚钢板焊接而成，由于所用钢板的长和宽比其厚度大很多，因此吊梁的结构分析可视为线弹性平面应力问题，可采用四节点直边四边形单元进行有限元分析，其力学模型如图1所示，可以简化为吊梁上方的吊耳孔固定，下方4个吊耳处受到集中载荷P的平面板。吊梁的几何参数有：梁的长度L、边缘高度b1、中心高度b2、厚度t，材料参数包括弹性模量E和泊松比λ，载荷参数为P，运用板壳单元对吊梁进行有限元参数化建模，由于吊梁的结构为左右对称结构，因此，只需研究其一半的结构响应。

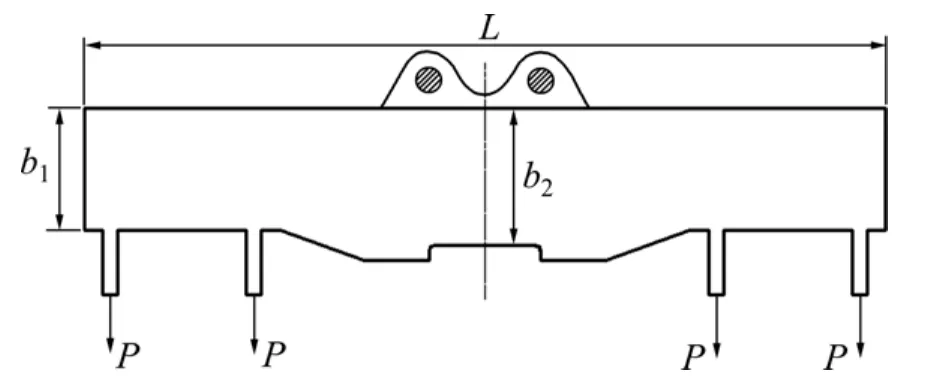
图1 吊梁的力学模型Fig.1 Mechanical model of hanging beam

2 区间有限元

区间有限元方法的基本思想是以区间数学为基础，将区间分析方法引入到结构分析中，当结构的不确定变量可以由区间界定时，即可建立区间有限元法。

2.1 区间有限元法的基本原理

根据有限单元位移法中，位移的控制方程可表示为Ku=F(其中：K为对称劲度矩阵；u为位移向量；F为载荷向量)。由于结构的设计参数具有不确定性，从而导致控制方程中的K和F也成为不确定性矩阵和向量，因此具有不确定性有限单元的位移控制方程可以表示为：

当结构设计参数在一个范围内变化，则结构不确定性可用区间来描述，即其中： αI为区间向量； αl和 αu分别为区间向量下界和上界。因此，由不确定参数向量α确定的区间有限元控制方程为

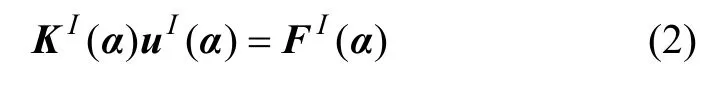
其中：KI(α)为结构整体劲度区间矩阵；FI(α)为整体载荷区间列向量；uI(α)为结构位移区间列向量。

对弹性结构，应力σI通过材料的本构关系和协调方程可由变形唯一确定，即

其中：EI为与单元材料相关的弹性区间矩阵；D为线性微分算子。

2.2 区间有限元控制方程的解法

由于区间有限元控制方程中总体刚度矩阵不再是确定的，不能用传统位移法来获得结构的区间响应，致使控制方程的求解较为困难，因此，其求解方法也就成为不确定问题区间分析的关键[8-9]。

由于区间运算的复杂性，为了能够更准确的获得解区间，一些学者提出了一些新的求解方法：端点组合法[10]、区间矩阵摄动法及子区间摄动法[11]、区间参数优化法[12]、区间迭代解法[13-14]等，但这些解法都有本身的局限性[15]。本文针对不确定参数之间可能存在的相关性，提出了利用一阶泰勒展开的方法来求解区间有限元控制方程。

根据式(2)可知：所要求解的结构响应为由不确定参数向量α来确定的区间变量uI(α)，若不确定参数向量α各元素之间不存在相关性，则uI(α)为线性表达式，可以直接用位移法来获得其解；若不确定参数α各元素之间存在相关性，则uI(α)为非线性表达式，可通过一阶泰勒展开近似：

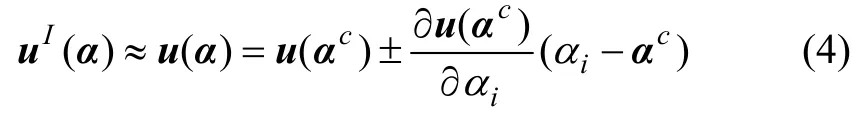
其中：αc为区间参数向量α的均值，即为不确定参数个数。

由式(1)可知：

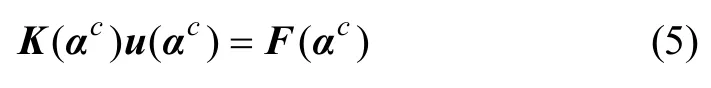
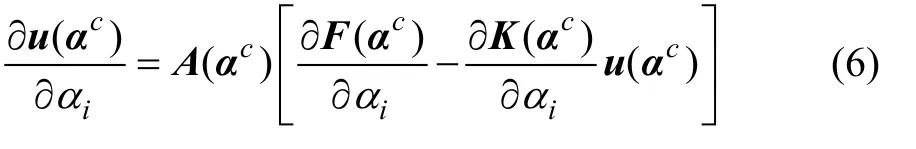
由式(6)可计算得到∂u(αc)/∂αi。由于αi∈α ，故可对式(4)进行区间自然扩张，可得到：

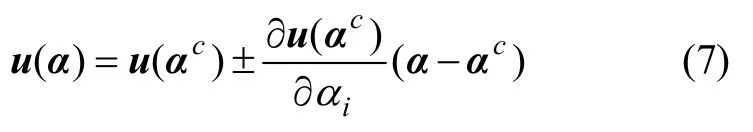
根据式(5)～(7)，可确定结构响应的上界和下界为：

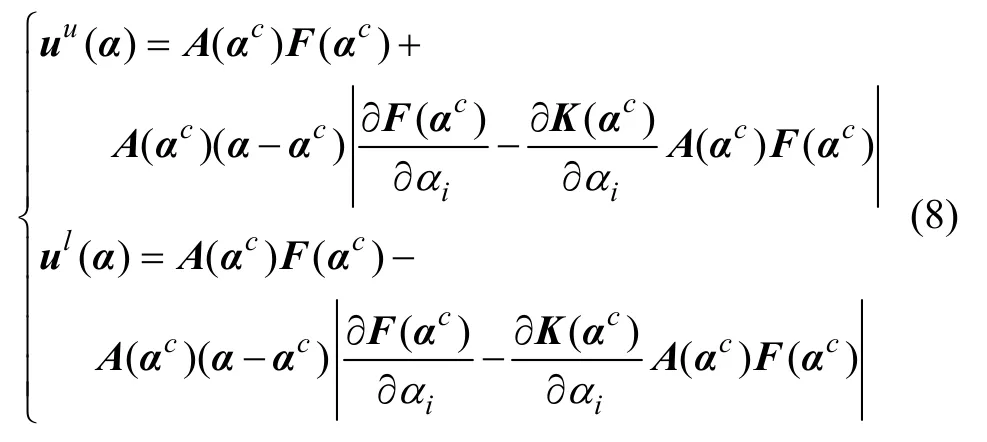
为了对上述方法进行验证，下面采用常用的6杆桁架结构为例来进行分析，如图2所示，其具体参数可参照文献[9]。按照式(8)计算，可得到节点2和3的位移上限和下限，如表1所示。

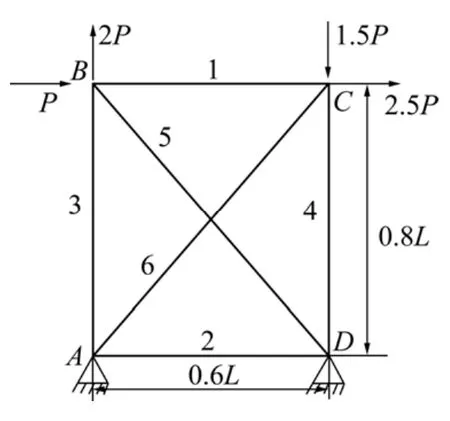
图2 6杆桁架结构简图Fig.2 6-bar truss structure

对表1计算结果分析，得出以下结论：

(1) 由 5种计算方法得出的节点位移分析可知，节点2和3在x和y方向的位移均值相差很小，说明对节点位移区间均值的求解具有一定的稳定性。

(2) 以区间参数优化法的求解结果作为准确解进行比较，可知对5种方法计算出的节点位移离差有一定的差别。以区间参数优化法作为准确解可知，端点组合法、区间矩阵摄动法、区间迭代法所得到的节点位移区间均大于区间参数优化方法的区间，不能很好地避免区间计算所产生的区间扩张，而本文方法确定的区间接近于区间参数优化法的区间。

(3) 与其他方法相比，本文方法在求解区间有限元控制方程时，仅需确定出矩阵K对α的偏导矩阵及逆矩阵即可，求解简便，计算量小，而且易于编程实现。

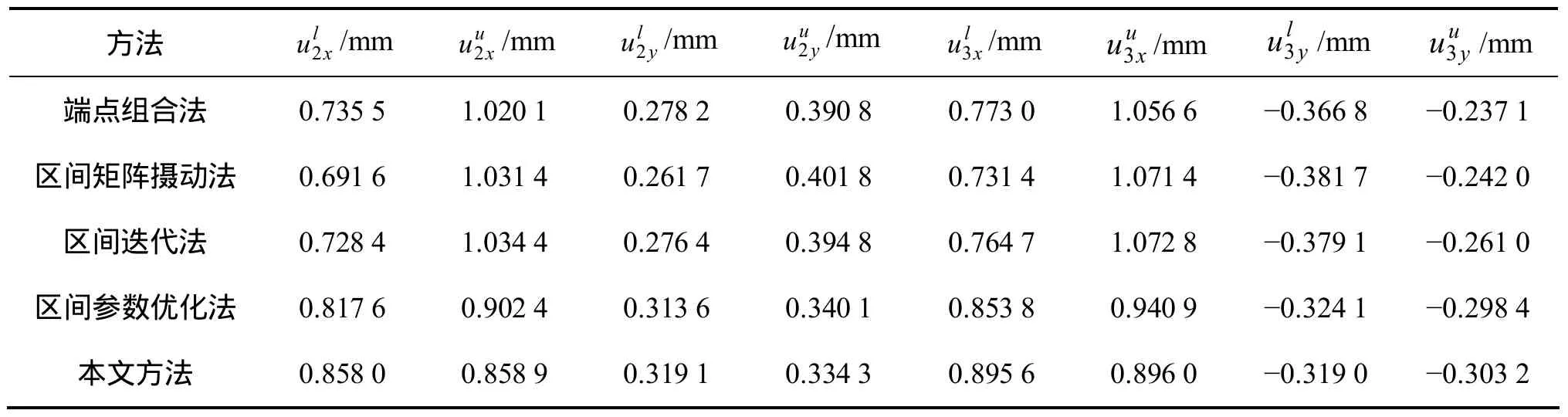
表1 6杆桁架结构的不确定位移Table 1 Interval of displacements of 6-bar truss structure

3 吊梁的非概率可靠性分析

根据吊梁的区间有限元计算结果，可得到吊梁在载荷 P的作用下的静态响应(位移、应力等)的区间范围，由此可继续研究吊梁结构的可靠性。

3.1 吊梁的可靠性验算

吊梁可靠性验算主要包括抗弯稳定性验算和抗扭稳定性验算。

(1) 抗弯稳定性是载荷P作用下吊梁中部不产生弯曲破坏，并且受力处的变形不能超过设计要求，防止产生强度失效和刚度失效，其数学表达式为：

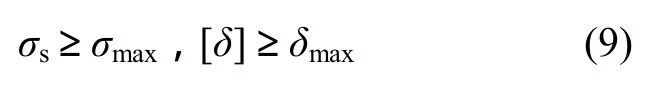
式中：σs为材料极限应力；σmax为吊梁最大应力值；[δ]为材料许用变形；δmax为材料最大变形值。

(2) 侧扭稳定性是作用在自由端的载荷P达到或超过一定数值时，避免吊梁的钢板发生侧向弯曲或侧扭破坏，防止产生失稳，其数学表达式为：

式中：Pcr为吊梁能所承受临界载荷。

综上所述，当吊梁的抗力(σs，[δ]，Pcr)分别大于它的作用响应(σmax，δmax，P)时，吊梁将处于可靠状态，由此可建立吊梁稳定性的极限状态方程为：

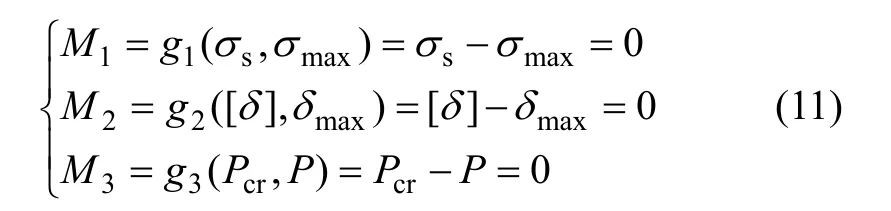
根据吊梁的设计可知：影响它稳定性的因素有几何参数(钢板厚度、长度及截面宽度)、材料参数(弹性模量，极限应力等)、载荷等，其中几何尺寸不确定性的来源主要是在设计参数与制造成型后的尺寸之间存在的误差，包括材料本身的误差(比如钢板的厚度)以及加工误差等；材料性能不确定性的来源主要是试验设备的影响以及检测手段的局限，以至于获得的材料物理参数有波动，通常在常规设计时只给出均值，是由许多检测值统计而得，由此可以认为材料的物理参数具有不确定性；载荷的不确定性主要是考虑到实际生产中所承受载荷的波动性。本文把这些不确定性因素描述为区间形式，从而建立吊梁的非概率可靠性分析方法。

3.2 吊梁非概率可靠性指标

确定影响吊梁可靠性的因素后，根据吊梁的失效准则来确定其功能函数为：

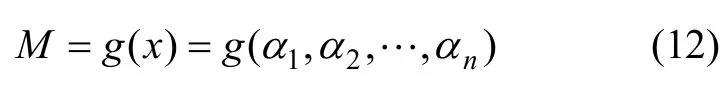
式中：iα的变化区间确定后，需对这些不确定因素标准化，来获得标准化区间内的区间参数，构成新的功能函数为：

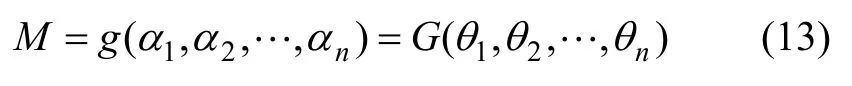
由式(14)可知：非概率可靠性指标 η的物理意义为：在标准化区间变量的扩展空间中，从坐标原点到失效面的最短距离作为非概率可靠性指标。对于任意在可行域中的不确定参数，当η＞1时，说明吊梁的安全域与失效域不相交，此时结构是安全的；当 η＜-1时，吊梁的安全域包含失效域，此时结构必然失效；当-1≤η≤-1时，吊梁是处于临界状态，从严格意义上讲，此时认为结构是不可靠的。因此，η愈大，吊梁愈可靠。

根据吊梁的极限状态方程(11)可以确定出各失效模式下非概率可靠性指标 η，包括弯曲失效的非概率可靠性指标η1、变形失效的非概率可靠性指标η2和侧扭失效的非概率可靠性指标η3，对于吊梁结构来说，只要其中一个失效发生，则整个吊梁即失效，因此，吊梁的非概率可靠性指标为η1，η2和η3的最小值，即η=min(η1, η2, η3)。

4 吊梁设计参数区间敏感性分析

根据非概率可靠性方法得到吊梁的可靠性指标，了解结构的可靠性程度后，如何通过对可靠性程度的控制来指导吊梁的设计呢？就需要对吊梁的设计参数作敏感性分析，可以定量的判断出不确定设计参数对吊梁可靠性的影响程度，从而揭示出提高可靠性应该修改哪些设计参数。

目前研究结构参数敏感性[18]的方法多为确定变量下敏感性分析方法，即采用局部梯度信息进行判断，忽略了设计变量的区间变化范围对其实际变化范围和不确定程度的影响。而区间敏感性分析测度的是设计变量区间的变化程度对结构响应区间的影响程度，即结构响应区间的产生多大的变化是由设计变量的区间性来决定的，因此，可以把表征不确定性的区间敏感因子定义为

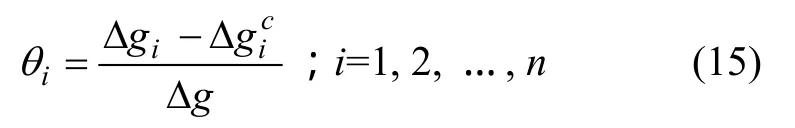
其中：Δgi表示第 i个不确定参数具有波动时所对应的状态函数波动范围表示第i个不确定量未波动时所对应的状态函数波动范围，为状态函数的波动范围，越大，表征结构响应对该变量的敏感性越高，反之就越弱。区间敏感因子的几何意义如图3所示。

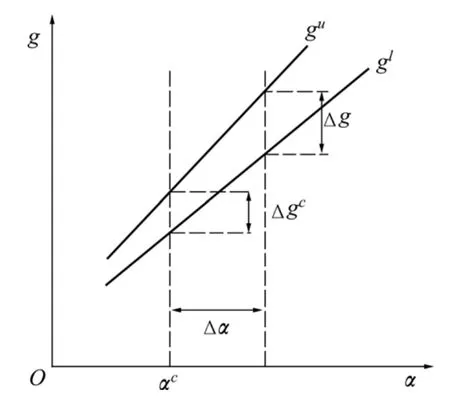
图3 区间敏感性方法Fig.3 Interval sensitivity analysis

从对吊梁可靠性验算分析可知：影响其可靠性程度的结构响应为最大变形σmax、最大应力δmax和临界载荷Pcr。因此，只需判断出设计变量区间在一定区间范围内，对结构响应的影响程度，即为设计参数相对于结构可靠度的敏感程度。

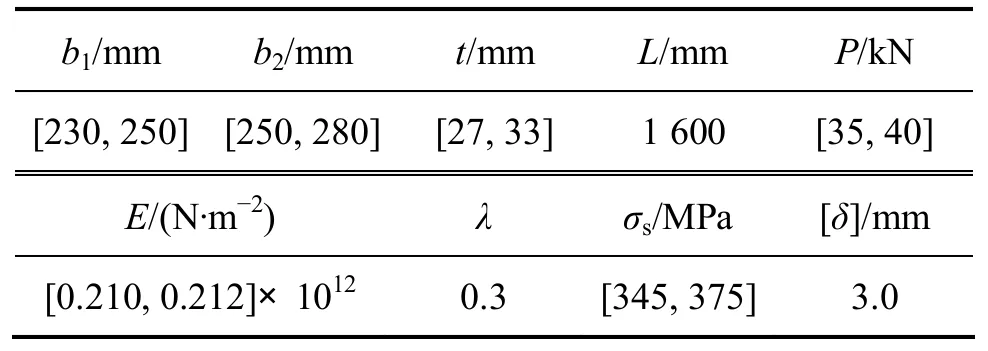
表2 吊梁的设计参数Table 2 Hanging beam design parameters

(2) 对吊梁模型进行单元划分，根据单元的个数对单元刚度矩阵进行组集，可获得整体刚度区间矩阵K(α)，把载荷P等效到吊梁节点上，确定载荷区间向量F。

(3) 刚度区间矩阵K(α)和载荷区间向量F对区间向量α中每个参数求偏导数，代入区间有限元控制方程(8)，获得吊梁的结构响应。

吊梁的应力和变形能够由上述步骤得到，产生屈曲的临界载荷[19]可以通过下式求得：

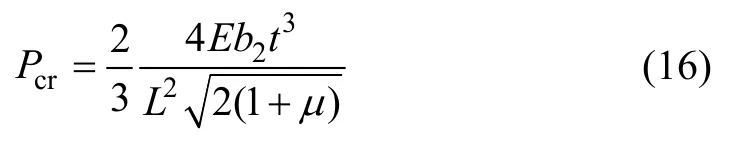
在不同失效模式下结构响应的上限和下限如表 3所示，根据非概率可靠性方法得到不同失效模式下的非概率可靠性指标。

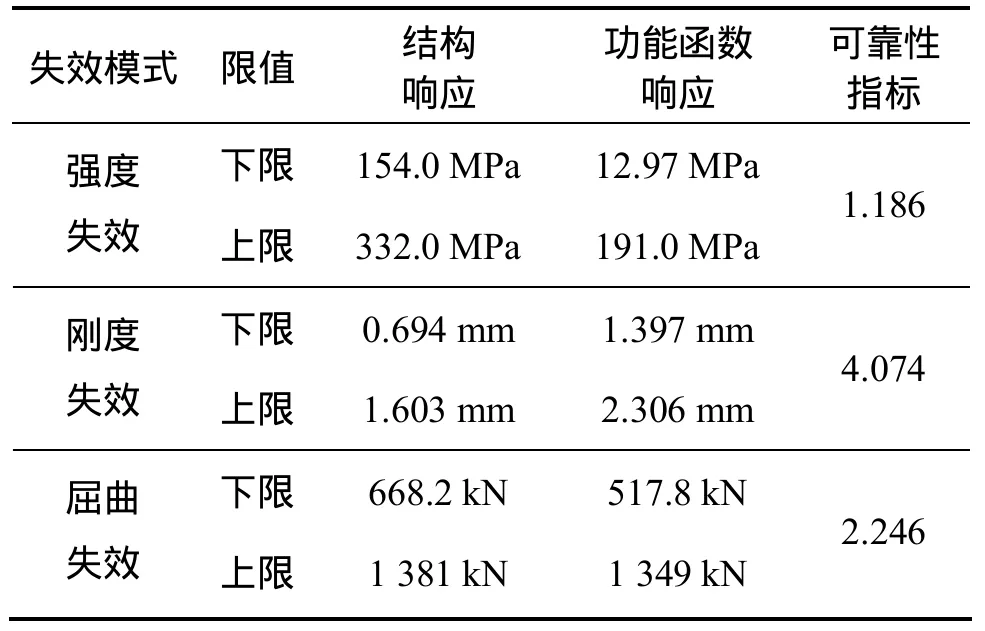
表3 吊梁的响应区间及可靠性指标Table 3 Interval responses and reliability indexes of hanging beam

5 实例分析

以图1所示的吊梁为例，其设计参数如表2所示，根据设计要求，吊梁的极限应力为 σs和许用变形为[δ]，在载荷P的作用下，对其结构进行区间有限元计算，并分析其可靠性以及对设计参数的敏感性。

(1) 计算得到不确定变量向量的均值cα，对吊梁进行参数建模，根据平面板单元的有限元计算方法，确定有限元模型中的单元刚度矩阵Ke(α)。

对不同失效模式下的非概率可靠性指标进行分析可知：吊梁的整体结构可靠性指标η=min(η1, η2, η3)=η1＞1，表明吊梁的3种失效方式均不会发生，因此，吊梁的设计参数在所给定区间内波动，能够满足设计要求，是完全可靠的；3种失效模式的可靠性指标关系为 η2＞η3＞η1，其中吊梁的强度可靠性指标最小，表明其强度失效是整个结构最主要的失效模式，因此，在设计时需要对结构强度要求多加注意。

为了进一步探讨吊梁的不确定参数向量对可靠性的影响规律，结合各失效模式下的状态方程，在各个不确定参数在区间内波动的情况下，对吊梁的结构响应(应力、变形和临界载荷)的影响程度，即吊梁不确定参数的敏感性分析。通过对吊梁3种失效模式下区间敏感因子计算，给出了不确定参数向量的变异量在-0.5～+0.5之间的结构响应变化曲线，如图4～6所示。从图4～6可以看出：当不确定参数变异范围为0时，所有曲线都交于零点，敏感因子为0。图4中的应力敏感因子θ随厚度t和高度b2变异量的增加逐渐减小，表明厚度t、高度b2与结构应力成反比，同理，载荷P与应力敏感因子θ成正比，而高度b1和弹性模量E对应应力敏感因子的变化曲线趋近于 0，表明结构应力相对与高度b1和弹性模量E的变化不敏感。对于同一变异量，不确定参数对应的敏感因子，其绝对值越大，则表面响应值相对于此不确定参数的敏感程度越高。图5和图6所示分别为位移敏感因子和临界载荷敏感因子随不确定参数的变化曲线。

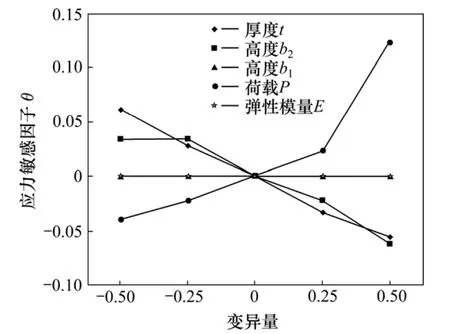
图4 应力敏感因子随不确定参数变化曲线Fig.4 Stress sensitive factor curve with uncertain parameters

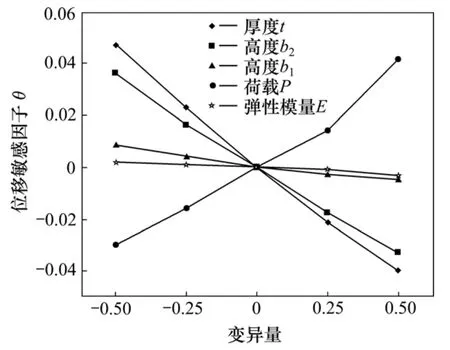
图5 位移敏感因子随不确定参数变化曲线Fig.5 Deformation sensitive factor curve with uncertain parameters

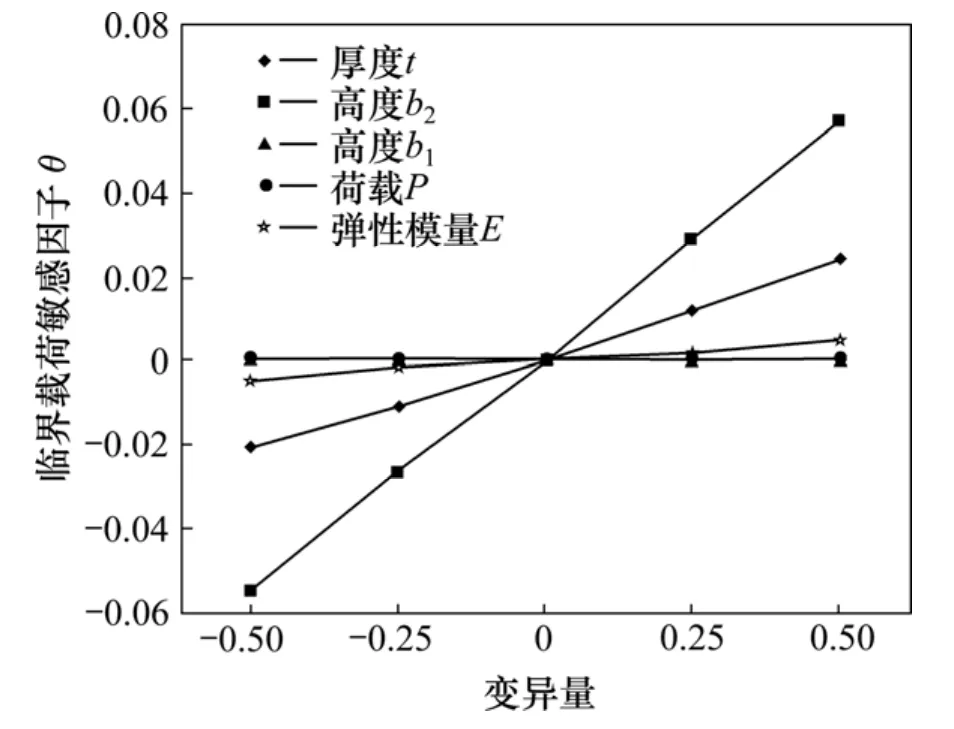
图6 临界载荷敏感因子随不确定参数变化曲线Fig.6 Critical load sensitive factor curve with uncertain parameters

从图4～6可见：在相同的变异范围内，应力敏感因子的值最大，说明不确定的参数的变化对吊梁结构的最大应力影响程度最高。因此，在设计参数选取时首先需保证强度要求，这与可靠性计算的结果相同。

6 结论

(1) 在对吊梁结构的受力模型进行分析的基础上，根据吊梁设计参数具有区间性，引入区间有限元法，建立了吊梁非概率可靠性分析方法。

(2) 针对区间有限元控制方程求解困难，提出了一种利用一阶泰勒展开算法来求解该方程，该方法能有效避免区间扩张，且运算简便。

(3) 强度失效是吊梁设计时最主要的失效模式，在对设计参数选取时，需对首先满足结构强度要求。

[1]段巍, 安利强, 徐飞.基于随机有限元——一次二阶矩的汽轮机叶片可靠度计算[J]. 华北电力大学学报, 2004, 31(3):104-107.DUAN Wei, AN Li-qiang, XU Fei. Reliability calculation of steam turbine blade based on SFEM and mean-variance method[J]. Journal of North China Electric Power University,2004, 31(3): 104-107.

[2]刘宁, 吕泰仁. 随机有限元及其工程应用[J]. 力学进展, 1995,25(1): 114-126.LIU Ning, LÜ Tai-ren. Stochastic FEM and its applications in engineering[J]. Advances in Mechanics, 1995, 25(1): 114-126.

[3]Rao S S, Sawyer J P. Fuzzy finite element approach for the analysis of imprecisely defined systems[J]. AIAA Journal, 1995,33(12): 2364-2370.

[4]SHAO Guo-jian, SU Jing-bo. Interval finite element method and its application on anti-slide stability analysis[J]. Applied Mathematics and Mechanics: English Edition, 2007, 28(4):521-529.

[5]CHEN Su-hua, YANG Xiao-wei. Interval finite element method for beam structures[J]. Finite Elements in Analysis and Design,2000, 34(1): 75-88.

[6]马娟, 陈建军, 徐亚兰, 等. 模糊随机结构有限元及可靠性分析的双因子法[J]. 西安电子大学学报, 2009, 36(1): 69-73.MA Juan, CHEN Jian-jun, XU Ya-lan, et al. Analysis of the finite element and the reliability of the structures with fuzzy-random parameters based on the two-factor method[J]. Journal of Xidian University, 2009, 36(1): 69-73.

[7]王洪武, 吴爱祥, 杨仕教, 等. 基于正交有限元的矿柱动态模糊可靠性分析[J]. 武汉理工大学学报, 2010, 32(9): 97-100.WANG Hong-wen, WU Ai-xiang, YANG Shi-jiao, et al. Analysis of ore pillar and application using concept of dynamic fuzzy reliability based on orthogonal finite element method[J]. Journal of Wuhan University of Technology, 2010, 32(9): 97-100.

[8]刘长虹, 陈虬. 模糊随机结构屈曲问题的区间有限元法[J].工程力学, 2004, 21(1): 52-55.LIU Chang-hong, CHEN Qiu. An interval finite element method for buckling analysis of fuzzy-stochastic structures[J].Engineering Mechanics, 2004, 21(1): 52-55.

[9]李金平, 陈建军, 朱增青, 等. 结构区间有限元方程组的一种解法[J]. 工程力学, 2010, 27(4): 79-83.LI Jin-ping, CHEN Jian-jun, ZHU Zeng-qing, et al. A method for solving the structural interval finite element equations[J].Engineering Mechanics, 2010, 27(4): 79-83.

[10]Rao S S, Berke L. Analysis of uncertain structural system using interval analysis[J]. AIAA Journal, 1997, 35(4): 727-735.

[11]苏静波, 邵国建, 刘宁. 基于单元的子区间摄动有限元方法研究[J]. 计算力学学报, 2007, 24(4): 524-528.SU Jing-bo, SHAO Guo-jian, LIU Ning. Static sub-interval perturbed finite element method based on the elements[J].Chinese Journal of Computational Mechanics, 2007, 24(4):524-528.

[12]王登刚, 李杰. 计算不确定结构静态响应的一种可靠方法[J].计算力学学报, 2003, 20(6): 662-669.WANG Deng-gang, LI Jie. A reliable approach to compute the static response of uncertain structural system[J]. Chinese Journal of Computational Mechanics, 2003, 20(6): 662-669.

[13]郭书祥, 吕震宙. 区间有限元静力控制方程的一种迭代解法[J]. 西北工业大学学报, 2002, 20(1): 20-23.GUO Shu-xiang, LÜ Zhen-zhou. An iterative method for solving the static governing equations of interval finite element method[J]. Journal of Northwestern Polytechnical University,2002, 20(1): 20-23.

[14]佘远国, 沈成武. 改进的区间有限元静力控制方程迭代解法[J]. 武汉理工大学学报: 交通科学与工程版, 2005, 29(2):248-251.SHE Yuan-guo, SHEN Cheng-wu. An improved iterative method for solving static governing equations of interval finite element method[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering, 2005, 29(2): 248-251.

[15]能肖文. 基于区间数学的有限元方法及其工程应用[D]. 南京:河海大学土木工程学院, 2005: 25-55.NENG Xiao-wen. Finite element method based on interval mathematics and its study of the engineering application[D].Nanjing: Hohai University. School of Engineering Mechanics,2005: 25-55.

[16]Ben-Haim M Y. A non-probabilistic concept of reliability[J].Structural Safety, 1994, 14(4): 227-245.

[17]郭书祥, 吕震宙, 冯元生. 机械静强度可靠性设计的非概率方法[J]. 机械科学与技术, 2000, 19(9): 106-107.GUO Shu-xiang, LÜ Zhen-zhou, FENG Yuan-sheng. A non-probabilistic reliability method for the design of mechanical components[J]. Mechanical Science and Technology, 2000, 19(9):106-107.

[18]苏静波, 邵国建, 褚卫江. 基于区间的土体参数敏感性分析方法研究[J]. 应用数学和力学, 2008, 29(12): 1502-1512.SU Jing-bo, SHAO Guo-jian, CHU Wei-jiang. Sensitivity analysis method of soil parameters based on interval[J]. Applied Mathematics and Mechanics, 2008, 29(12): 1502-1512.

[19]郑昌坝, 张洪海, 林志祥. 工字型截面悬臂钢梁的稳定性研究[J]. 力学与实践, 2007, 29(6): 56-59.ZHENG Chang-ba, ZHANG Hong-hai, LIN Zhi-xiang. On stability of I-section steel beam cantilevers[J]. Mechanics in Engineering, 2007, 29(6): 56-59.