民航管制员需求量预测方法研究
高 伟,黄慧敏
(中国民航大学空中交通管理学院,天津 300300)
近20年来,中国民航运输量一直保持着年均两位数的增长速度。空中交通服务网更加复杂,对民航管制员的需求进一步扩大。因此科学预测出民航管制员需求量对高校的管制员培养工作和管制单位的人才引进计划有着重要意义。
目前国内管制员需求量预测方法的研究正在兴起。本文根据近年来管制员数量的变化规律,通过建立灰色模型等数学预测模型,预测出未来5年内的民航管制员需求量,再通过比较预测结果的精确度,探索出其中一种较合理的需求量预测方法。
1 预测模型和建模方法研究
目前常用的人才预测模型可分为两类:①趋势分析模型,如灰色模型。根据一组历史数据内在的趋势规律,确定预测值。②相关分析模型,如回归模型。
1.1 灰色预测模型
灰色系统存在于信息完备的白色系统和信息全无的黑色系统之间,是一种获得了部分信息但是还不够完备的一种系统,在人力资源领域有着广泛的应用。数据列短小、趋势明显时,灰色预测精度较高。灰色模型[1-3]是一种指数曲线拟合抽象系统的逆过程,表示为GM(n,h),建模过程采用的是有原始数据生成的时间序列数据。
GM(1,1)的灰微分方程模型为

式中:Xk(0)为灰导数;Ek(1)为白化背景值;a为发展系数;b为灰作用量。
解得 GM(1,1)的预测模型为

1.2 用马尔科夫链理论改进灰色模型
马尔科夫链[4]常用于建模排队理论和统计学中的建模,是具有马尔科夫性质的离散时间随机过程,在该过程中,给定当前信息的情况下,过去对于预测将来是无关的。它满足以下两个假设:①t+1时刻系统状态的概率分布只与t时刻的状态有关,与t时刻以前的状态无关;②从t时刻到t+1时刻的状态转移与t的值无关。由于原始数据的起伏性、无序性及数据个数的有限性,灰色预测模型经常精度不够高,对于不具有明显指数规律的数据序列容易产生较大预测误差。因此可以利用马尔科夫链无后效性的特点改进灰色模型,提高预测精度。模型改进的基本思想是通过原始序列求得序列的状态转移矩阵,对未来的变化趋势做出估计。建模步骤为:
1)状态划分

其中

Ai和Bi视情况而定。
2)计算状态转移矩阵和转移概率矩阵
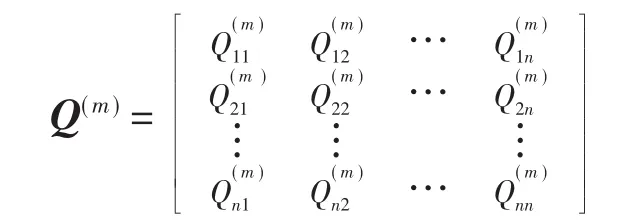
对Q(m)的第k行,若,则 Pj在下一时刻转移至Pd。
3)确定预测值
预测值区间[P1d,P2d]是由Pd确定的。区间中点为
2 预测结果和分析
本文依据2005—2010年航空运输量增长和管制员数量增长的数据,如表1所示,先利用灰色模型和改进模型预测,再和线性回归模型的预测结果相比较。
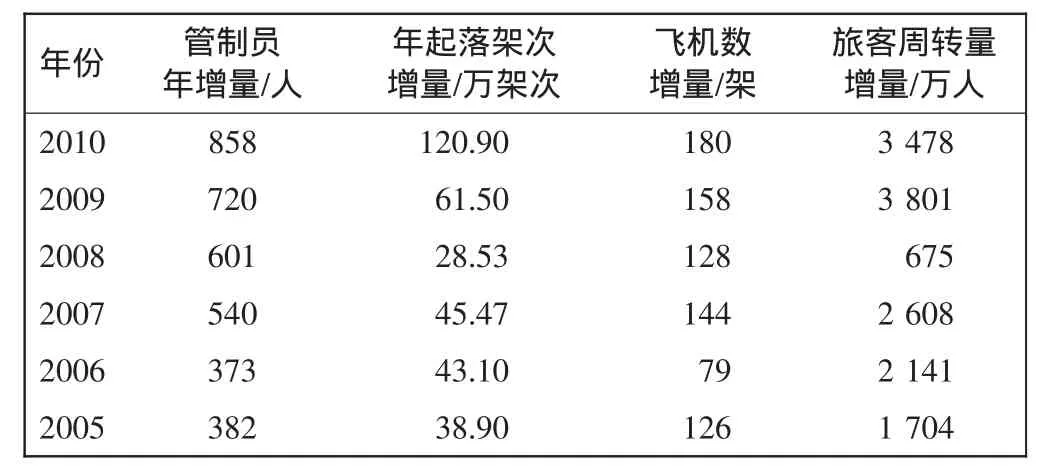
表1 管制员数量和航空运输量的增长数据Tab.1 Quantity growth data with the tuffic and contollens
2.1 用灰色模型GM(1,1)预测
根据表1中的管制员增量建立时间序列,因精度要求先对原始数据做一次开方处理[5],如表2所示。

表2 对原始数据的处理和误差分析Tab.2 Error analysis of initial data
可知原始数据精度较高,满足建模要求。
用最小二乘估计可得

从而得到 GM(1,1)模型为

将预测结果平方还原后得到灰色预测值,如表3所示。

表3 用灰色GM(1,1)模型得到的预测数据Tab.3 Forecast data of GM(1,1)model
2.2 用马尔科夫链改进的灰色模型预测
管制员数量具有一定的波动性和随机性,指数规律不明显。而马尔科夫链假设过去的内部状态变动的模式和概率与未来趋势一致,具有无后效性。用马尔科夫链改进原灰色模型,能更好地揭示出管制员增量的变化趋势。比较管制员增量的实际值和灰预测值,划分成3个状态,如表4所示。

表4 管制员增量状态划分表Tab.4 State division of controller growth

进一步得到状态转移矩阵

以2011年为例。2010年状态为 2,由 Q(1)得 2011年状态为1的概率为0.25,状态为2的概率为0.75,则2011年预测数据


表5 用改进模型得到的预测数据Tab.5 Forecast data of improved grey model
2.3 精度分析
对灰色预测模型和改进模型的预测值的精确度分析如表6所示。

表6 灰色预测模型与改进模型的误差分析Tab.6 Error analysis of Grey model and improved model
由表6可知灰色模型预测结果平均精度=97.962%,改进模型预测结果的平均精度=98.348%,都大于90%合格。而改进模型精度值更高,说明其比原模型的预测更可信。
回归模型是一种很常用的拟合方法,可用于精确度对照。管制员的增加与航空运输量的增长密切相关,根据民航业特点选取年起落架次增量X1、全国飞机增量X2、旅客周转量增量X3为自变量,由表1建立线性回归模型

计算结果如表7所示。
由表6和表7可知,回归预测误差较大,该方法可信度低。

表7 多元线性回归模型的误差分析Tab.7 Error analysis of multiple linear regression model
3 结语
本文在民航业快速发展的背景下,依据民航“十二五”规划,分析了近年来航空运输量和管制员数量增长的数据,建立了灰色模型、用马尔科夫链改进的灰色模型、回归模型等预测模型,预测了管制员需求量。由误差分析可知,马尔科夫链适用于改进灰色模型,进一步提高预测精度。笔者认为本文的预测结果可作为制定管制员培养计划的参考。
[1] 王明礼.三种灰色系统模型的预测比较[J].统计与决策,2011(8):35-37.
[2] 刘思峰,邓聚龙.GM(1,1)模型的适用范围[J].系统工程理论与实践,2000,5(4):121-124.
[3] 江志华,朱国宝.灰色预测模型GM(1,1)及其在交通运量预测中的应用[J].武汉理工大学学报(交通科学与工程版),2004,28(2):305-307.
[4] 刘次华.随机过程及其应用[M].3版.北京:高等教育出版社,2004:48-71.
[5]陈树德.用Excel求解灰色系统问题[J].彭城职业大学学报,2001,16(3):96-100.

