特定角域低增益的稳健方向图综合算法

王 勇 刘宏伟 纠 博 杨晓超

（西安电子科技大学雷达信号处理国家重点实验室，陕西 西安710071）

引 言

近年来，自适应阵列被广泛地应用于无线通信、声纳、雷达和医疗成像中［1］。由于非理想的阵列校正、互耦、相干或非相干的局部散射等因素的影响，自适应阵列往往存在各种误差，如角度误差［2］、校正误差［3］、通道幅相误差［4］等，这会对方向图综合的性能产生显著的影响［5］。因此，稳健的方向图综合技术是自适应阵列的一项重要研究内容。

根据加权方式的不同，稳健的方向图综合方法可以分 为 向 量 加 权 方 法［2，6－9］和 矩 阵 加 权 方 法［10－12］两类。对于向量加权方法来说，对角加载的采样矩阵求逆算法（LSMI）［13］是最常见的稳健算法之一。该算法通过对采样协方差矩阵加载一数量矩阵，能提高自适应算法的收敛速度和稳健性。但该算法最大的问题是加载量不容易简单地确定。基于最差性能优化的思想，文献［2］给出了一种基于二阶锥规划（SOCP）的稳健波束形成算法。该算法虽然能够对任意的导向矢量误差进行稳健处理并获得较高的信干噪比（SINR），但是该算法忽略了功率估计中的尺度模糊问题，功率估计性能较差［14］。与基于SOCP的稳健波束形成算法不同，稳健的Capon波束形成算法（RCB）通过约束导向矢量的l2范数解决了功率估计中的尺度模糊问题，因此，能够准确地估计出感兴趣信号的功率［14］。

虽然向量加权方法能够获得较高的SINR和较准确的功率估计，但其方向图参数，比如主瓣宽度和旁瓣电平，不能精确地控制或根据不同的需要进行灵活地调整［11］。为了能更灵活地控制方向图的参数，Li J.等提出了自适应矩阵 算法 （AMA）［10］。AMA算法通过约束方向图在主瓣角域和旁瓣角域的增益可以防止主瓣分裂并压低旁瓣，但当主瓣宽度给定后，其旁瓣电平不能被任意地压低［5］。另外，对于主瓣增益控制来说，AMA算法只是约束了方向图的主瓣宽度和增益，对信号源和阵列存在的未知误差不具有自适应的稳健性。为了使方向图的主瓣在存在误差时不分裂，文献［15］给出了一种基于半正定规划的稳健自适应波束形成算法（RAB－SDP）。该算法通过约束稳健角域的响应起伏，对角度误差具有很好的稳健性。但当阵列误差存在时，RAB－SDP算法的性能将下降。另外，当样本数较少时，RAB－SDP算法的方向图旁瓣较高。为了降低小样本对协方差阵估计的影响并提高RAB－SDP算法对阵列误差的稳健性，文献［5］结合最差性能优化思想和RAB－SDP算法提出了基于最差性能优化的RAB－SDP算法（RAB－SDP－WC）。该算法考虑了最差情况下的协方差阵估计误差对输出功率的影响，在约束主瓣响应起伏的同时最小化最差情况下的输出功率。RAB－SDP－WC算法虽然约束了稳健角域的响应起伏，但该约束并不能保证其在稳健角域的响应不衰减。另外，在实际应用中，根据一定的先验信息和特定需要，比如特定角域的密集干扰抑制，方向图需要在这些角域的增益较低［16］。为了在存在未知误差的情况下抑制密集干扰，文章提出了一种特定角域低增益的稳健方向图综合算法。

1 信号模型

考虑一个由M个阵元组成的等距线阵（ULA），相邻阵元间距为半波长。假设信号源从θ0方向入射到接收阵列上，则接收信号可以表示为［2，10－12］

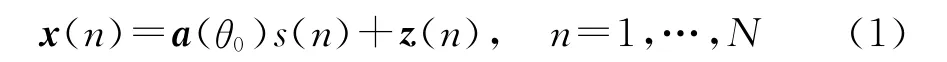
式中：N 表示快拍数；a（θ0）＝［1，exp（－jπsin（θ0）），…，exp（－jπ（M－1）sin（θ0））］T表示感兴趣信号的导向矢量，其中上标T表示转置操作；s（n）表示感兴趣信号在第n时刻的未知波形；z（n）表示第n时刻的干扰加噪声项。回波的协方差矩阵可以表示成R＝E｛xxH｝，其中上标H表示共轭转置操作，E｛·｝表示取期望运算。在实际中，R一般无法获得，通常用采样协方差矩阵来代替［13］

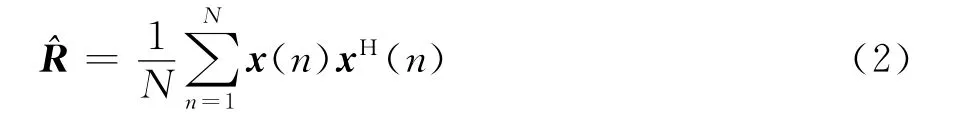
利用权矢量w＝［w1，…，wM］T对回波信号（1）进行加权可得

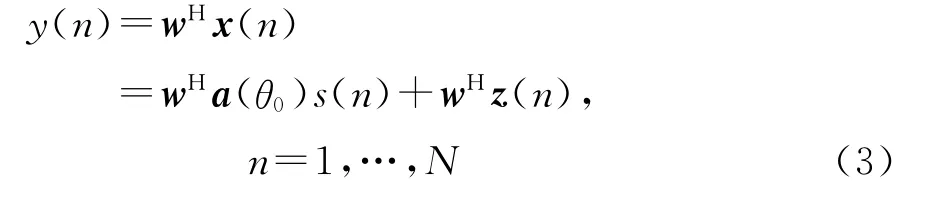
当信号的来波方向θ0已知时，Capon波束形成器基于如下的代价函数［14］

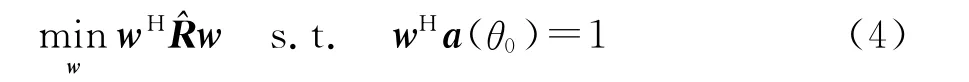
式（4）可以利用拉格朗日乘子法求解。当求出权矢量w0以后，可以利用＾σ20＝wH0＾Rw0估计出感兴趣信号的功率［14］。在方向图综合中，主瓣保形、低旁瓣是其重要的设计目标［12］。但这些约束对于w来说有些是非凸的，比如半功率点的增益的等式约束以及主瓣内增益的不等式约束［10］。显然，式（4）可以转化为

式中符号tr（·）表示求矩阵的迹。令T＝wwH，则式（5）等价于如下的优化问题［15］

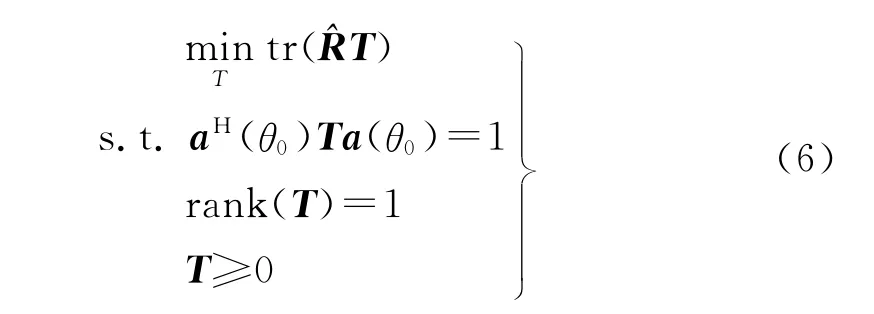
式中rank（·）表示取矩阵的秩。式（6）的优化问题是非凸的，因为有优化变量T的秩约束［11］。当去掉秩约束后，可以得到式（6）的半正定松弛（SDR）形式［15］

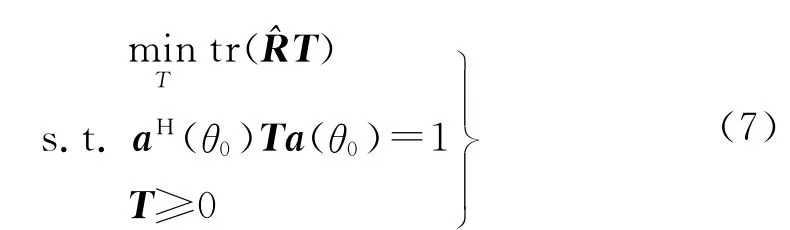
式（7）是一个半正定规划（SDP），可以利用凸优化工具包CVX［17］找到其全局最优解。另外，式（7）可以看作Capon波束形成器的矩阵加权形式。对于方向图综合算法来说，当自适应阵列存在未知误差时，必须考虑方向图对误差的稳健性［5］。根据一定的先验信息和特定需要，比如特定角域的密集干扰抑制，方向图需要在这些角域的增益较低［16］。

2 特定角域低增益的稳健方向图综合算法

在自适应阵列存在未知误差和样本数有限的情况下，考虑协方差阵估计误差对输出功率的影响。通过最小化最差情况下的输出功率可以得到待优化的目标函数（具体模型及推导见文献［5］）

式中：‖·‖F表示矩阵的F－范数；ε表示误差矩阵的F－范数的上界。与文献［5］、［15］给出的约束稳健角域的响应起伏不同，文中算法直接约束稳健角域的幅度响应不衰减，即

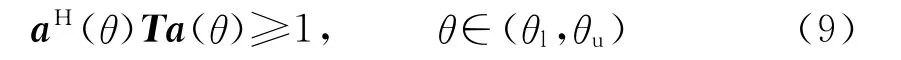
式中θl和θu分别表示稳健角域的下界和上界。显然，式（9）可以用来抑制角度误差，而且式（9）也保证了方向图的主瓣不会分裂。在实际应用中，根据一定的先验信息和特定需要，比如特定角域的密集干扰抑制，方向图需要在这些角域的增益较低［16］。为了保证方向图在给定角域的增益较低，还必须约束

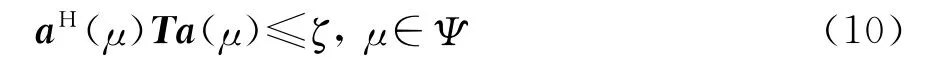
式中：Ψ表示给定的需要压低旁瓣的角域；ζ表示该角域响应的上界。结合式（8）、式（9）和式（10），可以得到文中算法的优化模型

式（11）可以看作式（7）的自然扩展，在约束稳健角域的幅度响应和特定角域的旁瓣响应的同时，最小化最差情况下的输出功率。由于ε随入射信号的功率变化，在后面的分析中用归一化的参数εr＝εM／tr来代替ε［5］。式（11）是一个SDP问题，可以通过凸优化工具包CVX［17］求解其全局最优解。一旦求解出T，可以对T做奇异值分解得到权矩阵W［11］.

3 仿真实验

假设阵列是由M＝10个阵元组成的ULA，相邻阵元间距为半波长。快拍数N＝100.回波中包含5个干扰，干噪比（INR）均为20dB，来波方向分别为＝｛－55°，－53°，－51°，－20°，50°｝。接收机噪声为高斯白噪声。文章比较了5种算法的方向图 综 合 性 能：AMA 算 法［10］，RAB－SDP 算 法［15］，RAB－SDP－WC算 法［5］，RCB 算 法［14］和 文 中 算 法（11）。RCB算法的导向矢量误差的l2范数的平方上界为εc＝0.35M.假定感兴趣信号的方位角为θ0＝0°，功率为σ20＝10dB.回波中一直包含感兴趣信号。在下面的仿真中，阵列方向图是通过1次实验得到的，而信干噪比和功率估计则是通过100次蒙特卡洛实验平均得到的。AMA算法关于方向图控制的参数如下：半功率波束宽度为10°，相应的旁瓣区是（－90°，－18°）和（18°，90°），峰值旁瓣电平为－15dB.RAB－SDP算法、RAB－SDP－WC算法和文中算法的稳健角域均为（－5°，5°）。对于一个给定的起伏 量 r＝0.3dB，RAB－SDP 算 法 和 RABSDP－WC算法在稳健角域的响应起伏的上下界可分别由U＝10r／20和L＝10－r／20确定［15］。假设根据一定的先验信息，文中算法需要压低旁瓣响应的特定角域为（－60°，－40°），而且该角域的旁瓣电平不能大于ζ＝－40dB.

仿真1：方向图性能（见图1和图2，其中横虚线表示0dB，6条竖虚线分别表示信号和5个干扰的来波方向）

在本仿真中，假设存在3°的角度误差，即信号的真实来波方向为3°.图1给出了文中算法在不同的归一化参数εr下的方向图对比结果。另外，为了说明在不同的参数εr文中算法对处于（－60°，－40°）之间的3个相邻较近的干扰的抑制能力，图1还给出了方向图在角域（－55°，－51°）之间的增益放大图。从图1可以看出，由于约束稳健角域的响应不衰减，所提算法对角度误差具有很好的稳健性。当εr＝0时，文中算法的旁瓣较高，因为在这种情况下，其对有限样本引起的高旁瓣问题不能抑制。但当εr＞0时，文中算法不但能够精确地控制方向图的主瓣响应和特定角域的低增益，而且能很好地抑制有限样本引起的方向图高旁瓣问题。

图1 文中算法在不同归一化因子下的方向图

图2比较了εr＝0.1时上述5种算法的方向图。为了比较5种算法对处于（－60°，－40°）之间的3个相邻较近的干扰的抑制能力，在图2中还给出了方向图在角域（－55°，－51°）之间的增益放大图。从图2可以看出，文中算法在保证信号来波方向的响应不衰减的同时，很好地抑制了干扰，特别对于处于（－60°，－40°）之间的3个相邻较近的干扰，通过压低该角域的旁瓣响应很好地将其抑制了。其他4种算法只是通过最小化输出功率在干扰方向自适应地形成零陷来抑制干扰，由于处于（－60°，－40°）之间的3个干扰在方位上相距较近，方向图并不能在这3个干扰的来波方向都形成零陷，此时其他4种算法对这3个干扰，特别是－55°和－51°的这两个干扰的抑制能力较差。另外，AMA算法只约束半功率点内的方向图增益大于－3dB，在信号的真实来波方向的增益并不是无畸变的［10］。RAB－SDP算法的旁瓣较高，因为RAB－SDP算法只约束了稳健角域的响应起伏，并没有考虑有限样本引起的协方差矩阵估计失配的影响［5］。

仿真2：输出SINR对归一化参数εr的敏感性

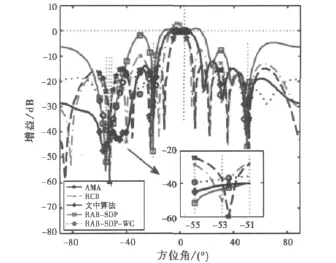
图2 文中算法和其他四种算法的方向图比较

在本仿真中，仿真条件与仿真1的相同。从文献［5］可知，由于协方差矩阵的估计误差的F－范数未知，因此稳健算法的性能最好对参数εr不敏感。图3给出了文中算法在不同的快拍数下随归一化参数εr的变化曲线。从图3可以发现，对于样本数为无穷的情况，即使εr＝0，文中算法也有很好的性能。因为其不但对角度误差稳健性很好（见图1的方向图），而且样本数为无穷时方向图不存在高旁瓣问题。对于样本数有限的情况，εr＝0时文中算法的性能较差，因为此时方向图存在高旁瓣。但当εr≠0以后，由于考虑了有限样本引起的协方差矩阵估计误差的影响，其输出SINR对εr的变化不敏感。

图3 不同快拍数下文中算法的输出SINR随归一化参数εr的变化曲线

仿真3：输出SINR随校正误差方差的变化关系

假设信号的来波方向准确已知，而阵列存在校正误差［3］，即其中误差矢量e的每个元素服从均值为0方差为的复高斯分布。图4给出了文中算法在不同的归一化参数εr下的输出SINR随的变化曲线。从图4可以看出：只要εr＞0，所提算法对校正误差方差的变化比较稳健。

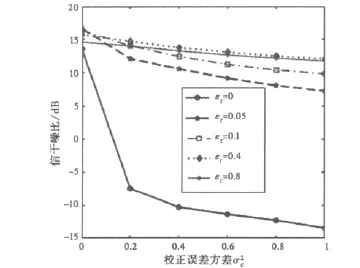
图4 不同的归一化参数εr下文中算法的输出SINR随校正误差方差的变化曲线

仿真4：文中算法和其他4种算法的输出SINR对比

在本仿真中，仿真条件与仿真3的相同。图5比较了文中算法和其他4种算法的输出SINR随校正误差方差σ2e的变化曲线。从图5可以看出：文中算法的输出SINR在σ2e的变化范围内都高于其他4种算法，因为其通过约束（－60°，－40°）的旁瓣响应将处于其间的3个相邻较近的干扰很好地抑制了，而且还保证了阵列在信号的来波方向的响应不衰减。RCB算法只有当校正误差的l2范数的平方小于参数εc时性能较好，但当校正误差较大，特别是超出εc所确定的不确定集时，性能有较大的下降。AMA算法由于只约束方向图的参数［10］，对误差不具有自适应的稳健性，因此性能较差。RAB－SDP算法只约束了稳健角域的响应起伏，对校正误差和有限样本引起的协方差矩阵估计误差不具有稳健性，性能最差。RAB－SDP－WC算法考虑了校正误差和有限样本对协方差矩阵估计的影响，因此性能要好于RAB－SDP算法和AMA算法。

仿真5：文中算法和其他4种算法的功率估计对比

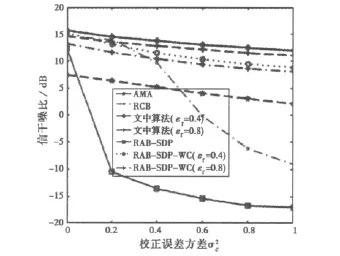
图5 不同算法的输出SINR随校正误差方差的变化曲线

在本仿真中，假设存在5°的角度误差，即信号的真实来波方向为5°.此时RCB算法的参数εc＝0.5M.表1给出了不同样本情况下5种算法的输出SINR和功率估计。当样本数为无穷（理想的协方差矩阵）时，参数εr＝0.001；当样本数为10时，εr＝0.2.从表1可以看出：当理想的协方差矩阵已知时，5种算法的功率估计都较准确，但文中算法的功率估计更准确。另外，由于协方差矩阵为理想的协方差矩阵，RAB－SDP算法不受有限样本引起的高旁瓣影响，此时RAB－SDP算法和RAB－SDP－WC算法的输出SINR只相差0.02dB.AMA算法由于只约束半功率点的响应大于－3dB，在信号的来波方向增益不是无衰减的，而且对（－60°，－40°）内的3个干扰的抑制能力较差（见图2），因此，输出SINR最低。虽然RCB算法的功率估计对参数εc不敏感［14］，但是由于导向矢量误差的l2范数的平方ε0＝15.230 2大于参数εc，输出SINR较差。与前4种算法相比，文中算法的输出SINR更高。当样本数较少时，RAB－SDP算法由于高旁瓣问题功率估计和输出SINR都有较大的下降。其他4种算法很好地抑制了小样本引起的方向图高旁瓣问题，因此，在小样本情况下功率估计与样本数无穷时相比基本没怎么下降。在这种情况下，文中算法的功率估计仍然是最准确的。另外，在小样本情况下，文中算法的输出SINR虽然相比样本数无穷的时候有所下降，但在5种算法中仍然是最高的。AMA算法和RCB算法的输出SINR虽然对样本数的变化不敏感，但对于较大的角度误差，它们的输出SINR始终比文中算法低。

表1 不同样本情况下五种算法的信号功率和SINR估计

4 结 论

文章提出了一种特定角域低增益的稳健方向图综合算法。该算法不但保证了稳健角域的响应不衰减和特定角域的低旁瓣，而且考虑了有限样本和未知误差对协方差矩阵估计的影响。仿真结果表明所提算法具有很好的稳健性、较高的输出信干噪比和较准确的信号功率估计。

［1］HUDSON J E.Adaptive Array Principles［M］.Stevenage：Peregrinus，1981.

［2］VOROBYOV S A，GERSHMAN A B，LUO Z Q.Robust adaptive beamforming using worst－case performance optimization：a solution to the signal mismatch problem［J］.IEEE Transactions on Signal Processing，2003，51（2）：313－324.

［3］XU L，LI J，STOICA P.Target detection and parameter estimation for MIMO radar systems［J］.IEEE Transactions on Aerospace and Electronic Systems，2008，44（3）：927－939.

［4］王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京：清华大学出版社，2004：416－418.

［5］ZHU L Y，GU Z H，ZHOU J J，et al.A robust adaptive beamformer based on worst－case semi－definite programming［J］.IEEE Transactions on Signal Processing，2010，58（11）：5914－5919.

［6］WANG F，BALAKRISHNAN V，ZHOU P，et al.Optimal array pattern synthesis using semidefinite programming［J］.IEEE Transactions on Signal Processing，2003，51（5）：1172－1183.

［7］焦永昌，杨 科，陈胜兵等.粒子群优化算法用于阵列天线方向图综合设计［J］.电波科学学报，2006，21（1）：16－20.JIAO Yongchang，YANG Ke，CHEN Shengbing，et al.Application of praticle swarm optimization in antenna array pattern synthesis［J］.Chinese Journal of Radio Science，2006，21（1）：16－20.（in Chinese）

［8］金荣洪，袁智皓，耿军平，等.基于改进粒子群算法的天线方向图综合技术［J］.电波科学学报，2006，21（6）：873－878.JIN Ronghong，YAN Zhihao，GENG Junping，et al.The pattern synthesis of antennas based on a modified PSO algorithm［J］.Chinese Journal of Radio Science，2006，21（6）：873－878.（in Chinese）

［9］刘聪锋，廖桂生.改进的快速稳健任意阵列天线方向图综合方法［J］.电波科学学报，2009，24（1）：104－110.LIU Congfeng，LIAO Guisheng.Improved fast robust pattern synthesis method for arbitrary arrays［J］.Chinese Journal of Radio Science，2009，24（1）：104－110.（in Chinese）

［10］LI J，XIE Y，STOICA P，et al.Beampattern synthesis via a matrix approach for signal power estimation［J］.IEEE Transactions on Signal Processing，2007，55（12）：5643－5657.

［11］XIE Y，LI J，ZHENG X，et al.Optimal array pattern synthesis via matrix weighting［C］／／IEEE International Conference on Acoustics，Speech and Signal Processing.Honolulu，HI，United States，2007：885－888.

［12］DU L，LI J，STOICA P.Signal power estimation via vector and matrix approaches［C］／／ 41st Asilomar Conference on signals，systems and computers.Pacific Grove，CA，United States，2008：1357－1361.

［13］CARLSON B D.Covariance matrix estimation errors and diagonal loading in adaptive arrays［J］.IEEE Transactions on Aerospace and Electronic Systems，1988，24（4）：397－401.

［14］LI J，STOICA P，WANG Z.On robust Capon beamforming and diagonal loading［J］.IEEE Transactions on Signal Processing，2003，51（7）：1702－1715.

［15］YU Z L，ER M H，SER W.A novel adaptive beamformer based on semidefinite programming（SDP）with magnitude response constraints［J］.IEEE Transactions on Antennas and Propagation，2008，56（5）：1297－1307.

［16］YANG Yixin，WAN Chunru.Adaptive beampattern synthesis based on null broadening［C］／／IEEE Antennas and Propagation Society Symposium.Monterey，CA，United States，2004：3996－3999.

［17］GRANT M，BOYD S.Matlab software for disciplined convex programming［CP／OL］.［2008－04－08］.http：／／stanford.edu／～boyd／cvx.