摩擦摆隔震支座阻尼特性研究

刘昕铭，王少华，严情木，李 冰

(西南交通大学机械工程学院，四川成都 610031)

摩擦摆支座是一种有效的干摩擦滑移隔震支座，作为建筑结构和桥梁的隔振器，受到了较为广泛的关注。其特有的圆弧滑动面具有自动复位功能，从而可以有效地限制隔震支座的位移，使其震后恢复原位，增加了隔震装置的可靠度。

目前，欧洲、美国、日本和我国均在桥梁抗震规范中采用了隔震设计［1-3］。在等效静力分析方法、单自由度反应谱法、多自由度反应谱法中，若等效刚度、等效阻尼比取值适当，可得到满意的设计结果［4］。由于摩擦摆隔震支座的非线性特性，在分析开始时设计位移是未知的，因而其等效刚度、等效阻尼比也是未知的。为得到满意的结果，等效阻尼比的取值极为重要。

1 摩擦摆支座有限元模型的建立

1.1 单元及材料定义

在ABAQUS中建模时，整个摩擦摆支座采用实体单元建模，由于接触问题不宜使用二次单元，故选用六面体八节点线性减缩积分单元(C3D8R)，该单元在合适的网格密度下，可以以较低的成本得出满意的结果［5］。支座钢材的泊松比 ν=0.3，弹性模量取 E=2.1 ×105MPa。

1.2 接触定义

准确的摩擦行为是模拟摩擦摆支座的基础。滑块从黏结条件下进入初始滑动的摩擦系数不同于已经处于滑动中的摩擦系数。在Explicit求解器中选择指数衰减规律来模拟理想的黏结—滑动摩擦行为。

1.3 加载情况

由于摩擦摆支座轴对称，施加的位移载荷为水平单向，可利用支座的对称性取二分之一模型进行研究，在对称面上施加对称载荷。上支座板与滑块的相对运动相当于一个球形铰，它的主要功能是通过转动调整位置，使支座不发生倾覆，故应约束上支座板的转动自由度。在模拟试验机加载时，约束支座底面的所有自由度，对上支座板施加水平正弦位移载荷。在模拟地震载荷时，支座的底面仅需约束竖直方向的自由度。地震激励直接施加在支座底部。有限元模型见图1。

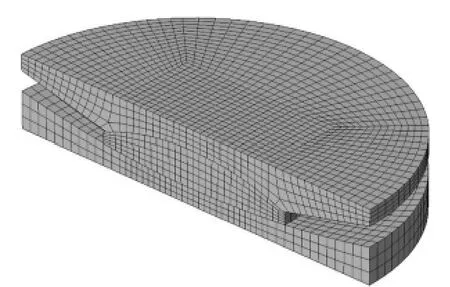
图1 摩擦摆支座的有限元模型

2 摩擦摆支座等效阻尼比的理论研究

摩擦摆支座在循环加载下形成的滞回曲线直观地反映了支座的耗能机理，如图2所示。其中，Ki为支座的初始刚度;Kh为支座的摆动刚度;Keff为支座等效刚度。滞回曲线围成的面积为支座在一个循环下消耗的能量。

当振动系统中存在非黏性阻尼时，通常用一个等效黏性阻尼系数ce来进行近似计算。等效黏性阻尼系数的值是通过单个周期内非黏性阻尼所消耗的能量We和等效黏性阻尼所消耗的能量Wr相等的原则计算得出。黏性阻尼力在稳态强迫振动Asin(ωt－α)的一个周期内所做的功为［6］在稳态振动中，作用力输入给体系的能量被摩擦力所耗散，其耗散的能量为滞回曲线所包围的面积，即

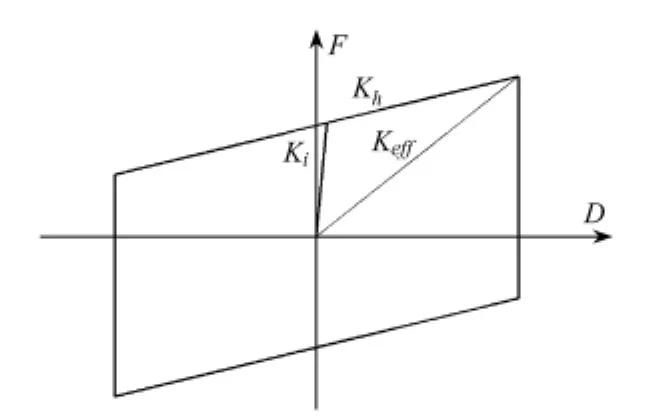
图2 摩擦摆支座的滞回曲线

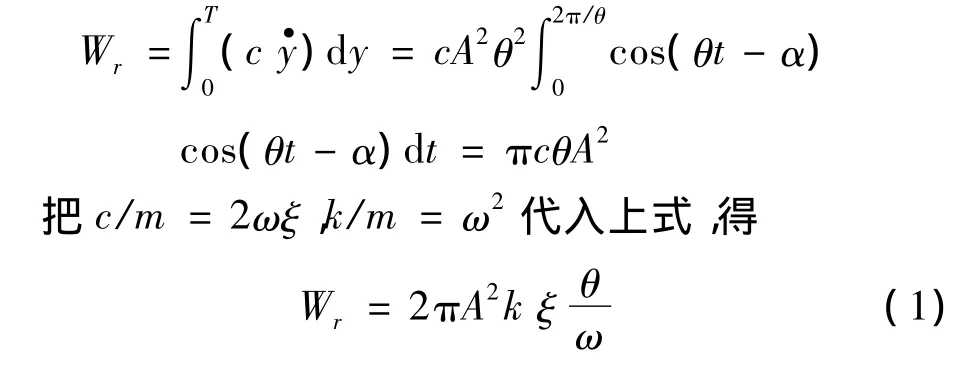
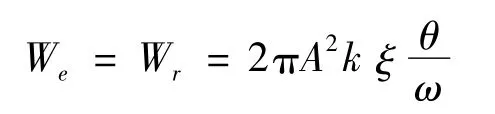
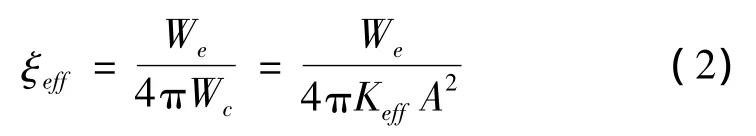
式中，We为摩擦摆支座在一个循环内的耗能，Wc为摩擦摆隔震支座的总应变能，支座等效为线弹性模型后，用等效刚度表示为Wc=KeffA2。

3 动态仿真结果分析

通过改变支座的滑移量、滑道半径、摩擦系数及竖向压力，研究各参数对支座阻尼比和耗能特性的影响。

3.1 水平滑移量对阻尼比、耗能的影响

如图3所示，R=1 m，μ=0.1，N=40 kN 时，支座的摆动刚度在滑移量较小的情况下为线性增大，随着滑移量的增大呈非线性增长。图4给出了滑移量与等效阻尼比、耗能之间的关系。当滑移量从0.05 m增大到0.20 m时，等效阻尼比下降的趋势明显，之后衰减逐渐缓慢，虽然等效阻尼比随滑移量增大而减小，但每个循环的耗能却线性增加。滑移量增大的同时滞回曲线的面积也增大，故耗能增大。

3.2 滑道半径对阻尼比、耗能的影响

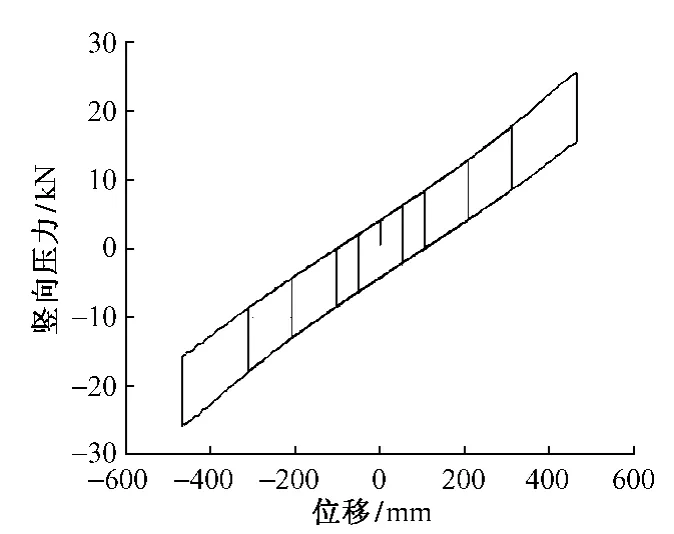
图3 滑移量对滞回曲线的影响

图4 阻尼比、耗能与滑移量相关曲线

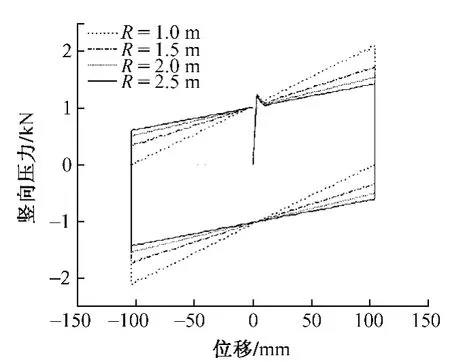
图5 滑道半径对滞回曲线的影响

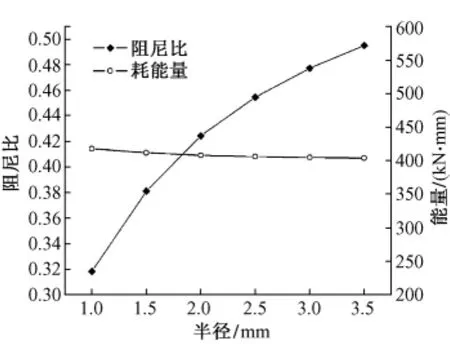
图6 阻尼比、耗能与滑道半径的相关曲线

如图5所示，μ =0.1，N=10 kN，D=0.1 m 时，滑道半径的增加降低了支座的摆动刚度，却未影响初始刚度。如图6所示，当滑道半径从1 m增大到2 m时，等效阻尼比增长明显，随着半径的继续增加，对其敏感性降低。由于改变滑道半径不影响初始刚度，滞回曲线的面积几乎没有变化，故每个循环的耗能基本不变。

3.3 摩擦系数对阻尼比、耗能的影响

如图7所示，N=10 kN，D=0.1 m，R=1 m 时，随着摩擦系数的增加支座的初始刚度线性增加，摆动刚度不变，滞回曲线的面积也增加。如图8所示，随着摩擦系数的增大，等效阻尼比较为平均地增长且每个循环下的耗能线性增长。

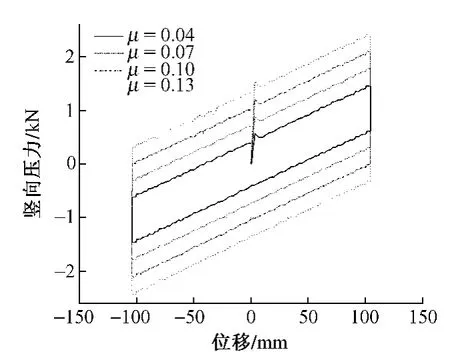
图7 摩擦系数对滞回曲线的影响

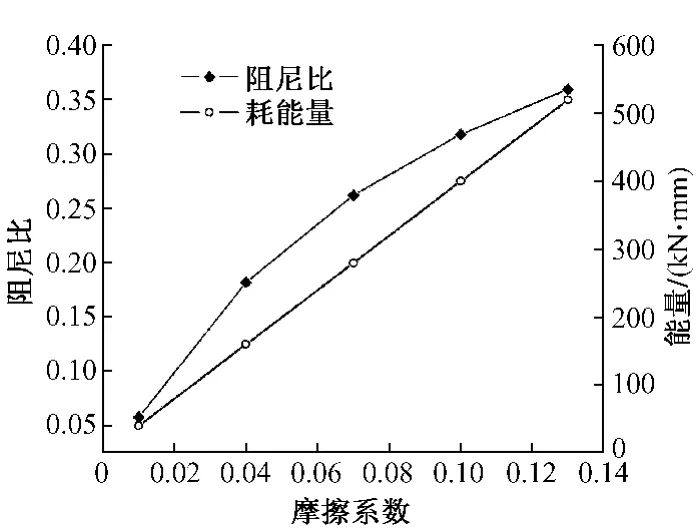
图8 阻尼比、耗能与摩擦系数的相关曲线

3.4 竖向压力对阻尼比、耗能的影响

如图9所示，D=0.1 m，R=1 m，μ=0.1时，增加上支座板承受的竖向压力不仅影响到支座的初始刚度，同时会增加支座的摆动刚度，有效地增加了滞回曲线的面积。虽增加了耗能，但也提高了摆动刚度，故竖向压力几乎不影响支座的阻尼比，见图10。

图9 竖向压力对滞回曲线的影响

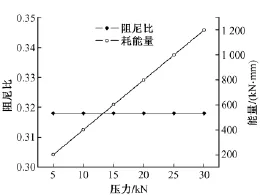
图10 阻尼比、耗能与压力的相关曲线

4 等效线性化研究

在隔震桥梁的计算中，由于使用了隔震装置，从而使上部结构的变形类似于一个刚体，且隔震支座变形为主要变形，桥墩所占变形比例很小［4］。借助等效线性化模型进行分析时，等效刚度、等效阻尼比直接取决于隔震支座的位移;而支座的位移变化情况较为复杂，则选择合适的位移至关重要。本文采用单自由度结构作为摩擦摆隔震支座的等效线性模型，系统的振动方程如下

将有限元时程分析得到的结果作为支座的精确响应，本文用ABAQUS对支座的有限元模型进行动态仿真，输入EI-Centro地震波得到支座的最大位移响应Dmax，代入式(2)求得等效阻尼比ζ1。用Matlab对式(4)进行弹性时程分析得到此时系统的最大位移为D1(表1)。由表1可知，根据支座在最大响应时的等效参数建立线性模型，计算得出的最大位移D1大于Dmax，且随着摩擦系数的增加，误差从μ=0.01时的14.6%增加到μ=0.1时的115.2%。其原因是随着摩擦系数的增加，支座的耗能能力增强，故在地震响应中将更多地处于“黏滞”状态，而方程(4)得到质点的运动始终是振动的，不能反应实际响应中的“黏—滑”状态。故利用Dmax计算的等效阻尼比偏小。

式(4)可以求得线性模型的最大响应与非线性时程分析的最大响应相等时的等效阻尼比ζ2，将ζ2代入式(2)求得对应的位移D2，用该位移计算的等效阻尼比可以较准确地表示支座的阻尼特性。如表1所示，当摩擦系数足够大时，“黏滞”占整个响应的比例很大，此时支座并没有发挥应有的隔震作用，例如当μ=0.055时，为使线性模型的最大响应等于Dmax，D2取极小值;若继续增大摩擦系数，ζ2将大于支座最大阻尼比63.7%，若继续使用等效线性法计算，是不可行的，对于这种情况，应选用时程分析法。

表1 计算结果对比

5 结论

1)计算结果表明，摩擦摆隔震支座的等效阻尼比与滑移量成反比，与滑道半径、摩擦系数成正比。竖向压力几乎对等效阻尼比没有影响，但等效阻尼比的大小并不能明确表示能量耗散的多少，而是反应耗能水平的指标。

2)当选取恰当的等效刚度和等效阻尼比时，可以用线性方法计算结构的最大地震响应。由于在分析前无法确定隔震支座在地震作用下发生的位移值，所以无法确定等效线性化参数。而直接用支座最大位移响应计算出的等效阻尼比偏小。

3)线性化方法并不适用于任何情况，当支座运动状态的“黏滞”占主导时，应采用非线性时程分析法，同时，摩擦摆隔震支座的最大等效阻尼比不应超过63.7%。

［1］AASHTO．Guid Specifications for Seismic Isolation Design［S］．Washington D．C．:AASHTO，2000．

［2］中华人民共和国交通部．JTG/J B02-01—2008 公路桥梁抗震设计细则［S］．北京:人民交通出版社，2008．

［3］王月钱，钟铁毅，顾正伟，等．E型钢支座对铁路简支梁桥隔震效果研究［J］．铁道建筑，2010(9):21-23．

［4］范立础．桥梁减隔震设计［M］．北京:人民交通出版社，2001．

［5］庄茁．基于ABAQUS的有限元分析和应用［M］．北京:清华大学出版社，2008．

［6］谢官模．振动力学［M］．北京:国防工业出版社，2007．

［7］R克拉夫，J彭津．结构动力学［M］．北京:高等教育出版社，2006．