基于双层规划的农资供应链覆盖率优化

张 磊，李 莉，尤建新

（同济大学 经济与管理学院，上海200092）

我国农资企业大多单独分散经营，未形成完善的供应链，彼此之间缺乏相应的联系，市场竞争力弱.我国农业生产和农村生活的分散性决定了农资产品物流体系的分散性.地域的不同及自然条件的差异，导致农业生产具有明显的地域性和季节性特点.农村的发展仍相对落后，在道路交通条件、信息网络平台、商品仓储能力上都与大城市有很大的差距.基于农资行业特点，一些学者尝试将现代物流理论引入农资产品流通领域，研究涉及农资供应链工厂选址、网络规划、仓储运输等方面.农资供应链工厂选址是供应链发展的关键，选址方案就是要分析出工厂数量、位置和规模，及物流量在各下游客户间的分配.国内外学者对工厂选址问题已有大量研究.

Curry和Skeith首先提出选址分配问题，工厂选址问题不仅决定地理位置，还要考虑如何最优地把产品配送到物流中心或直接配送到各个需求点［1］.此后，研究者将该问题扩展到多服务站点、多阶段的研究［2－3］，又有学者将此问题的约束条件加以限制使之更加切合实际.选址分配模型只解决了工厂的位置和规模，但不能决定工厂的数量.覆盖问题可分为集覆盖问题和最大覆盖问题两类.覆盖问题最早由 Roth［4］和 Toregas等［5］提出，主要应用于消防、急救等公共事业.由于集覆盖问题要求设施能够覆盖所有的需求点，这会造成设施数量过大而超过企业的实际承受能力，Church等［6］提出了最大覆盖问题.研究者已将最大覆盖问题改进，将其应用于更多不同的情形［7］，目前求解最大覆盖问题的方法也已很多，但未考虑选址中的竞争问题.即只考虑设施对被覆盖点的覆盖，未考虑被覆盖点对设施的选择.同时考虑竞争和覆盖的选址问题的研究相对较少.Zvi Drezner等［8］提出逐渐覆盖问题，并将此概念引入竞争选址问题中.王丹等［9］建立在竞争环境中基于最大覆盖模型、考虑价格决策的最大收益模型.目前，竞争选址的研究主要针对价格或距离（或时间），将这两个因素同时考虑时，还没有很好的方法确定二者的权重.何波等［10］考虑最小化总成本以及最大化顾客覆盖率，建立双层规划模型来设计逆向物流网络.双层规划模型的引入使供应链选址从决策者和客户双方利益考虑，提高了客户服务水平.

综上所述，以往论文已分别解决了工厂选址的数量、位置、规模和分配这4个方面的问题，但能同时解决这4个方面的模型还很少.本文将选址分配问题和最大覆盖问题同时引入双层规划模型，并结合农资供应链的特点来确定农资供应链的工厂数量、位置、规模和分配.模型以顾客覆盖最大为基础、选址总利润最大为目标，引入时间和距离的敏感度变量反映竞争环境中客户在选择供应商时对运输距离和产品价格的敏感程度，优化以往的覆盖选址问题.

1 问题描述

农资供应链工厂选址问题：农资供应方的核心企业总公司拟在全国建立总产能为Q的一个或多个分厂，现仅考虑两阶段的供应链：从工厂至分销网络中心.现有I个候选厂址，需满足J个供应链内部客户——分销中心的需求.工厂的总数、投资总额有限制，工厂的利润与其销量、年产能、产品市场价格、原材料价格及运营成本有关，其中工厂年产能受投资额影响，产品市场价格是一个服从某种分布的随机变量.工厂生产不同产品的工艺高度类似，故可视为单产品选址.原材料及产成品的体积相近，故可统一计算库存.

考虑到整个市场竞争，候选建厂的地点会有已存在的竞争者（仅考虑分厂与一个产品替代者之间的竞争）.分销中心对距离和价格的敏感度、分厂与竞争者离分销中心的距离、分厂与竞争者对分销中心的供货价格会影响分销中心对分成和其竞争者的选择.

经过对上述问题情境的分析，可推断本问题属于考虑竞争的覆盖选址分配问题，其自身特点：①选址，对地理位置己知的备选工厂进行取舍；② 分配，需将分销商分配到工厂，规定一个分销中心的需求可以由多个工厂满足；③ 竞争，考虑到激烈的市场竞争，本文在选址之初就将竞争者考虑在内，以保证新建厂址对竞争者有竞争优势.

2 模型假设

本文模型基本假设如下：① 存在若干个备选工厂，分销中心的位置、数量及需求已定，因原材料至工厂的运输费用由供应商承担，已归入原材料成本，故可不考虑工厂距供应商的距离.本文只研究两阶段的供应链，即工厂至分销中心；② 产品需求的概率分布已知，各分销商的需求不存在相关性；③ 只考虑一种产品的生产运输；④ 运输费用与运输量成正比，由厂商承担；⑤ 每个分销商可由多个工厂提供产品；⑥ 所建工厂均按设计产能满负荷生产；⑦新建工厂有最大覆盖距离，若分销商位于覆盖范围以外，则厂商无法向此分销商提供产品，厂商对客户的覆盖率下降，导致服务水平下降.

3 模型的建立与说明

上层目标从决策者的角度出发，使工厂的总利润最大，通过收入减去产品成本、初建费用及从备选地点工厂运至分销商的运输费用而获得；下层目标从使用者的角度出发，使工厂在竞争环境中对分销商的覆盖率达最大，从而提高服务水平.模型如下：

模型中符号含义如下：U（0），L（0）分别表示上、下层规划模型；i为工厂序号，I＝｛i｜i＝1，2，…，I｝为备选工厂集；k为竞争者工厂序号，K＝｛k｜k＝1，2，…，K｝为已有竞争者的工厂集；j为分销商序号，J＝｛j｜j＝1，2，…，J｝为现有的分销商集；F为所有新建工厂的总利润；ps为产品出厂价格，它是一个服从某种分布的随机变量，可对市场价格进行统计分析，拟合度检验得出；v为分销商能够被满足的需求量；pt为单位产品的成本，包括原材料成本、人工成本以及库存成本等；b为工厂的标准单位产能，设新建工厂有m种产能选择，则新建工厂的产能可为0b，1b，2b，…，mb；Yim为0，1变量，当在i地点建m个单位产能的工厂时Yim＝1，否则Yim＝0；l为运输方式的种类，取值可为1、2、3、4，分别表示公路、铁路、航空、内河水路为第l种运输方式下，i地点的工厂运往第j个分销中心时的单位运输费用；Gj为第j个分销商的需求量；fim为在i地点新建第m种产能的工厂的固定建设费用；Qi为第i个工厂的产能；B为所有新建工厂的初始投资预算；Q为所有新建工厂的设计总产能；N为新建工厂的数量.qij为0，1变量，当分销商j能被位于i地点的分厂覆盖时qij＝1，否则qij＝0；dij为i地点的分厂与分销商j之间的距离；dkj为竞争者分厂k与分销商j之间的距离；p0为竞争者给分销商的供货价格，可通过市场调查获得；αj为分销商j对距离的敏感度，o≤αj≤1，αj越大，表明分销商j对距离越敏感；βj为分销商j对价格的敏感度，o≤βj≤1，βj越大，表明分销商j对价格越敏感；αj＋βj＝1；hij为分销商j对i地点分厂的决策因子，∀j；hij＝αjdij，min＋βjps；hkj为分销商j对竞争者分厂k的决策因子，hkj＝αjdkj，min＋βjp0，因此

上层规划第1项为单位产品出厂价格与总销量之积，即为所有新建工厂的总利润.其中总销量通过下层规划对客户的最大覆盖量得到.第2项为单位产品总成本与设计总产能之积，即为所有新建工厂的产品总成本.其中b表示工厂的标准单位产能，设新建工厂有m种产能选择，则新建工厂的产能可为0b，1b，2b，…，mb.在i地点的工厂产能为bYi1＋则所有新建工厂的总产能为本文假设工厂为满负荷生产，则所有新建工厂的总产量即.第3项为运输成本，设有l种运输方式，表示第l种运输方式下，i地点的工厂运往第j个分销中心时的单位运输费用，则总运输费用.第4项为所有新建工厂的初建成本，其中fim表示在i地点新建第m种产能的工厂的固定建设费用，α表示因存在规模效应，随着产能的增加，固定建设费用增加量边际递减，用α（0＜α＜1）衡量固定建设费用增加量，因建单位产能的工厂的固定建设费用为fi1＝kbα［11］，则建有m产能的工厂的固定建设费用为fim＝k（mb）α＝mαkbα＝mαfi1，因此在i地点新建工厂的固定建设费用为fim其中.下层规划最大化对分销商的覆盖，即在考虑了竞争的情况下，最大化分销商能够被满足的需求量.

约束说明：第1个约束保证每个新建工厂的产能不少于分销商对其需求量.第2个约束保证新建工厂的成本不超过其初始投资预算.第3个约束保证新建工厂总产能不超过设计总产能.第4个约束限制新建工厂的数量.第5个约束为变量的0－1约束.第6个约束保证只有在该地点拟建工厂，才能从该地点为分销商提供产品.

4 模型求解分析

由于上层模型的目标函数依赖于下层模型的解，而且双层规划模型属于NP－hard问题，因此双层规划模型求解比较困难.另外，由于模型具有非凸性，因此求得的解可能会是局部最优解.针对双层规划主要算法有灵敏度分析、模拟退火、支撑函数法，这些算法的主要问题是计算过程复杂而且容易陷人局部最优.辛亚峰采用遗传算法求解交通网络设计双层规划模型取得了较好的效果［12］，与灵敏度分析法相比此算法具有设计简单、全局性好的特点.本文采用遗传算法求解考虑物流服务水平的工厂选址双层规划模型具体设计思路：对上层模型的决策变量进行染色体编码，通过求解下层模型计算上层模型的适应函数，对上层模型染色体进行复制、交叉、变异，最终得到最优解.

5 实例应用

某复合肥企业根据发展战略，在整合现有产能的基础上，重新兴建工厂以实现产能的扩大.本文采取双层规划工厂选址模型求解.根据以往销售数据，现有三个备选工厂：备选工厂1位于山东平原；备选工厂2位于广西贵港；备选工厂3位于吉林.产品出厂价格ps＝2 500元，竞争者价格p0＝2 500元.运输方式的种类数（现暂只考虑汽运）l＝1.工厂的标准单位产能b＝30×104t，产能选择种类m＝2.单位产品成本pt＝1 600元，所有新建工厂的初始投资预算B＝25 000万元，所有新建工厂的设计总产能Q＝1×106t.新建工厂的最多数量N＝2.分销商j对距离的敏感度αj和分销商j对价格的敏感度βj都为0.5.l＝1，这里只研究汽车运输方式.

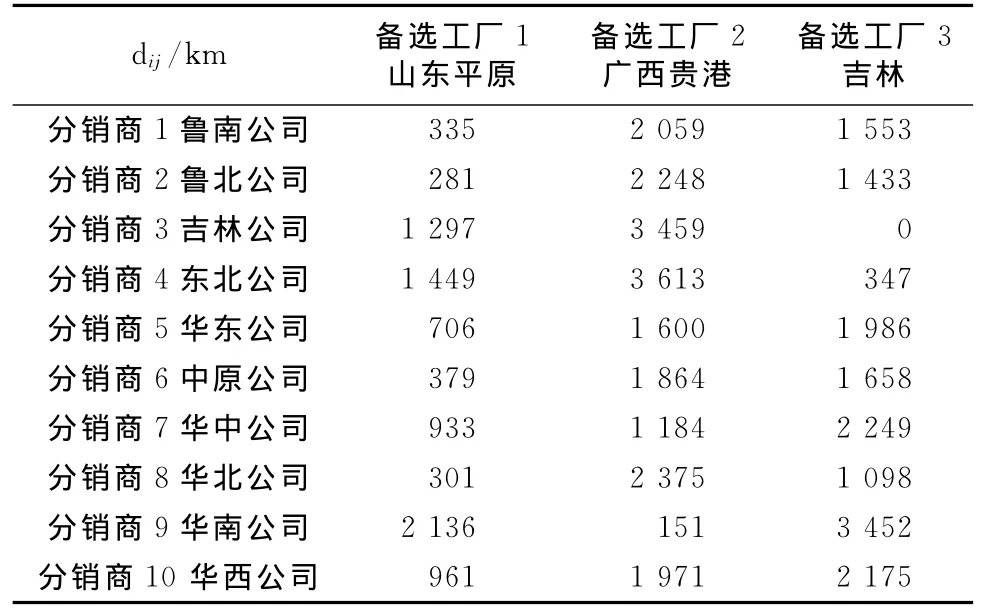
表1 备选工厂与分销商之间的距离Tab.1 Distance between the optional plants and distributors

竞争者分厂地址选择方式：山东、江苏和湖北是全国前三位的复合肥生产和销售大省，因此在这3个省中分别选择了最大的复合肥生产企业所在的城市.竞争者工厂1位于山东临沂，竞争者工厂2位于湖北荆门，竞争者工厂3位于江苏常州.

5.1 数据采集

根据以往的销售数据和调研数据进行模型数据的采集，根据公司企业的情况分析，采用基于双层规划的工厂选址模型.选址目标从3个备选工厂地址中找出1个或2个用于建厂；备选工厂数量i＝3，每个备选工厂有一个对应的竞争者k＝3，分销商数量j＝10.i地点的工厂与分销商j之间的距离（dij）见表1；竞争者工厂k与分销商j之间的距离（dkj）见表2；第l种运输方式，i地点工厂运往第j个分销中心时单位运输费用（）见表3；在i地点新建第m种产能的工厂的固定建设费用（fim）见表4；第j个分销商的需求量（Gj）见表5.

表2 竞争者工厂与分销商之间的距离Tab.2 Distance between the plants of competitors and distributors

表3 汽运方式下的单位运输费用Tab.3 Unit costs of transportation under the way of trucks

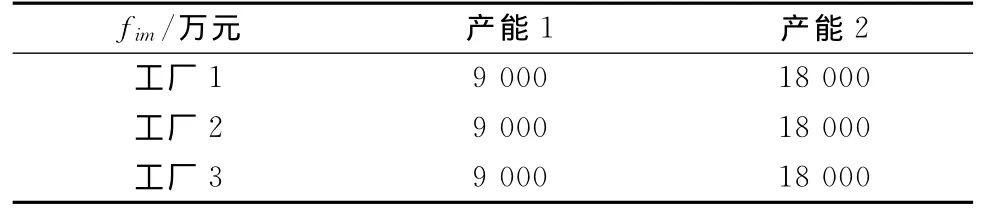
表4 备选工厂不同产能的固定建设费用Tab.4 Fixed construction cost of optional factory with different production capacities

5.2 运行结果

本模型采用遗传算法，采用工具 Matlab Version 7.1Service Pack 3进行优化求解.交叉概率：0.85，变异概率：0.05，初始种群：30，后代次数：100.结果显示：

表5 分销商需求量Tab.5 Demand of distributors t

即分销商1鲁南公司、分销商2鲁北公司、分销商3吉林公司、分销商4东北公司、分销商7华中公司、分销商9华南公司能被备选工厂1山东平原覆盖，分销商1鲁南公司、分销商2鲁北公司、分销商4东北公司、分销商5华东公司、分销商6中原公司、分销商8华北公司、分销商10华西公司可被备选工厂2广西贵港覆盖，分销商3吉林公司、分销商4东北公司、分销商6中原公司、分销商7华中公司、分销商8华北公司能被备选工厂3覆盖.

即分销商1鲁南公司、分销商2鲁北公司、分销商5华东公司、分销商6中原公司、分销商10华西公司需求量的一半和分销商8华北公司的全部需求量被指派给备选工厂2广西贵港.

决策变量：

即在备选地点2广西贵港建产能1类的工厂，亦即在广西贵港建产能30×104t的工厂.

结果显示：Fmax＝3.915 5×108，即新建工厂后的总收益为3.915 5×108元.可见模型求解结果符合实际情况，模型具有实际应用意义.

6 结论

农资供应链工厂选址应该注意以下问题：首先，出于利益的考虑，新建工厂要规划好总产能以及对分销商的供货分配，应该以最少的成本实现最大的收益，即实现供应链总利润最大.其次，由于农资产业品牌集中度低，新建工厂对顾客的覆盖率就显得越发关键.能覆盖到更多的顾客就意味着有更大的机会占领市场.第三，由于农资产业竞争激烈，在工厂选址之初就应考虑到竞争问题，以保证工厂建成之后能处于优势地位.第四，由于农资产品的季节性特点，在需求旺季，供应链对顾客需求的响应时间极其重要，适当缩短运输距离是节约时间的最直接方法.因此，本文在解决农资供应链工厂选址问题时应用双层规划，上层规划保证总利润最大，下层规划保证总顾客覆盖率最大.决策部门可以通过政策和管理来改变某个新建分厂的位置和物流成本，从而影响客户对是否从此新建分厂获得需求做出选择，但不能控制他们的选择.客户则对不同位置的工厂进行比较，根据不同分厂对自己需求的满足程度以及其服务的优劣来选择新建的工厂.弥补了一般选址问题中没有考虑客户对处于不同位置工厂进行选择这一缺陷.同时在下层规划时考虑了竞争问题，优化了传统的最大覆盖选址问题.

在模型的实例应用中，确定了备选工厂对分销商的供货价格，以后的研究可考虑将价格作为变量得出适合工厂的销售价格，为备选工厂的定价提供参考.

［1］任鸣鸣.供应链系统节点设施选址研究［D］.武汉：华中科技大学经济与管理学院，2008.REN Mingming.Research on facility location of supply chain system node［D］.Wuhan：Huazhong University of Science and Technology，2008.

［2］Geoffrion A M，Graves G W.Multicommodity distribution system design by benders decomposition［J］.Management Science，1974，20：822.

［3］Wesolowsky G O，Truscott W G.The multiperiod locationallocation problem with relocation of facilities［J］.Management Science，1975，22（1）：57.

［4］Roth R.Computer solutions to minimum cover problems［J］.Operation Research，1969（17）：455.

［5］Toregas C，Swain R，ReVelle C，et al.The location of emergency service facilities［J］.Operations Research，1971（19）：1363.

［6］Church R L，ReVelle C.Maximal covering location problem［J］.Papers of the regional Science Association，1974（32）：101.

［7］Revelle C，Scholssberg M，Williams J.Solving the maximal covering location problem with heuristic concentration［J］.Computers ＆Operations Research，2008，35（2）：427.

［8］Zvi Drezner，Wesolowsky G O，Tammy Drezner.The gradual covering problem［J］.Naval Research Logistics，2004（51）：841.

［9］王丹，马云峰.竞争与合作设施并存的最大覆盖选址问题［J］.武汉理工大学学报：信息与管理工程版，2010，32（4）：628.WANG Dan，MA Yunfeng.Maximal covering location problem with coexistence of competitive and cooperative facilities［J］.Journal of Wuhan University of Technology：Information ＆Management Engineering，2010，32（4）：628.

［10］何波，杨超.基于成本／服务权衡的逆向物流网络设计问题研究［J］.中国管理科学，2008，16（4）：90.HE Bo，YANG Chao.Trade－Offs between cost and customer service in reverse logistics network design［J］.Chinese Journal of Management Science，2008，16（4）：90.

［11］Manne A.Investments for capacity expansion ［M ］.Cambridge：MIT Press，1967.

［12］XIN Yafeng.Genetic－algorithm－based approach bilevel programming models ［J］.Journal of Transportation Engineering，2000，3：115.