无物方信息的未检校近景影像的方位元素估计

周拥军，寇新建，朱建军

（1.上海交通大学 船舶海洋与建筑工程学院，上海200240；2.中南大学 测绘与国土信息工程系，湖南 长沙410083）

内外方位元素的估计问题是近景摄影解析处理的核心问题，近景摄影测量的短摄影基线、构形不规则及大角度摄影、多重叠等特点增加了定向的难度.对于量测相机或经预检校的普通相机，相机的内方位元素已知，若有一定数量的控制点，可以通过直接线性变换、空间后方交会等传统解析方法确定外方位元素.对于无物方控制点的立体影像序列则只能实现度量重建［1］，还需要通过绝对定向才能得到物方坐标.未检校相机的内方位元素未知，若采用传统方法，需要通过自检校［2］或广义相对定向［3］恢复内方位元素，然后经相对定向得到独立模型，通过模型连接得到统一模型，最后经绝对定向获取物方坐标.由于自检校得到的内方位元素精度低，加之多个独立模型的连接误差累积等影响，导致定向结果误差较大.

本文采用改进的层次重建方法，摄影过程中保持内方位元素不变，选用其中的1张影像的像空间坐标作为参考坐标系，通过3张以上影像的同名像点恢复投影矩阵和结构，然后采用基于绝对二次曲面的自检校方法恢复相机内方位元素，从而在无物方法得到物方坐标，该方法既可应用于低精度的三维重建，也可以作为高精度光束法平差的初值，是一种区别于传统定向方法的新方法.但由于无物方控制和不考虑畸变，因此定向的精度相对较低，只能用于低精度的测量或作为光束法平差的初值。

1 层次重建原理

现实世界的空间关系用欧氏空间来描述，若不考虑镜头畸变和其他误差的影响，相机成像模型满足射影变换关系，摄影测量中将成像模型表达为共线方程，若写成齐次坐标的形式，与视觉领域的针孔（Pinhole）成像模型是一致的，为表达方便，本文均用齐次坐标的形式表示.

设任一空间点的物方坐标为＝表示其投影得到的像点坐标，不考虑相机的畸变，则投影模型可表示为［1］

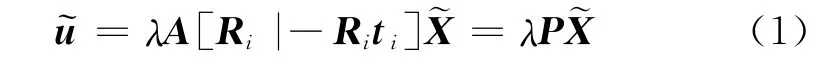
式中：A为相机的内部矩阵，若不考虑倾斜因子，共由4个独立参数构成，包括x、y方向上的比例因子αx，αy和像主点坐标u0，v0；Ri表示旋转矩阵；ti＝（tx tytz）T表示投影中心的物方坐标，Ri、ti统称为外方位元素，由6个独立参数组成；P为3×4的投影矩阵.

计算机视觉领域将几何变换分4个层次，即射影（Projective）变换、仿射 （Affine）变换、度量（Metric）变换和欧氏（Euclidean）变换，分别对应15，12，7，6个独立变换参数［4－5］.设某空间点变换前后的齐次坐标分别表示为变换关系表示为变换矩阵T为4×4的非奇异矩阵，对于不同层次的变换，T应满足不同的约束条件.层次重建的思路就是先利用立体影像的同名点进行射影重建，然后利用立体影像间的约束关系逐层过渡到欧氏重建.即先确定一个投影矩阵P和射影结构，使其满足很显然射影重建的结果不唯一，因为对于任一非奇异4×4的矩阵Q＝λPQQ－1也成立，层次重建的思想就是找到变换矩阵T，使其满足PT＝A［R｜－Rt］，其中，~XE为欧氏结构，R为旋转矩阵.近年来国内外学者采用改进的层次重建方法实现欧氏重建，如以平行透视或准透视代替通用的透视变换［6－7］，或考虑内方位元素改变的情况等［8］.

2 基于分解算法的射影重建

由投影关系式可知影像坐标受两种因素的影响，其一是投影矩阵，也称为相机的运动（motion）参数，其二是坐标，即结构（structure），从序列图像中恢复结构和运动是计算机视觉的一个基本问题.图像坐标是相机姿态和结构的双线性组合，如果其中一个因素保持不变，则像点坐标是另一因素的线性形式.分解方法就是基于这种考虑而得到的一种简洁高效的算法，它通过矩阵的奇异值分解（SVD）方法将图像测量矩阵分解成相机运动和三维结构分量.分解算法最早是由 Tomasi等［9］提出，Sturm，Heyden等改进了该方法［10－11］，并用于从序列图像中恢复运动和结构.

设有n个空间点，每个点在m幅图像中均有成像表示点i在第j幅影像的齐次坐标表示点i的射影结构，λij表示投影深度，则存在投影关系：

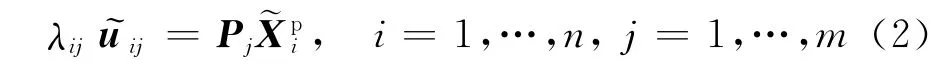
将所有像点组成一个联合矩阵，令P，X分别表示所有的投影矩阵和结构，则有：

由式（3）可以看出，矩阵Ws可以表示成3m×4的矩阵P和4×n的矩阵X的线性组合，因此Ws的秩应满足rank（Ws）≤4，当空间点的分布不存在奇异构形（共面或共线）的情况下，投影矩阵的秩应等于4.由于测量误差的影响使得Ws的秩大于4，需要找到一个秩为4的矩阵＾Ws逼近Ws，这可通过Ws的SVD分解实现，这就是基于分解算法的射影重建的思想，将Ws进行奇异值分解：

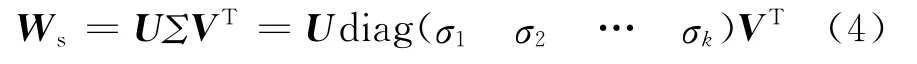
其中，k＝min（3m，n），σ1≥σ2≥…≥σk，U，V均为经svd分解后的矩阵，设U′和V′T分别表示U、V的前4列向量，则：

基于分解算法的射影重建过程归纳为以下步骤：① 将坐标归一化，即对所有像点uij（i＝1，…，m，j＝1，…，n）作相似变换或按文献［6］的规则选取归一化矩阵N；② 设所有尺度参数初值组成测量矩阵W；③ 将W进行奇异值分ss解，得到＾Ws；④ 根据计算尺度参数，并组成新的测量矩阵判断‖Ws－‖是否小于给定的限差，若大于限差则转入③继续计算，否则计算结束；⑤ 将投影矩阵进行逆变换得到N－1P.

3 方位元素估计

3.1 内方位元素估计

对于无任何物方控制的立体影像，需要通过自检校恢复内方位元素，视觉领域的自检校方法常采用基于绝对二次曲线和绝对二次曲面的自检校方法［5］，这里采用基于绝对二次曲面的自检校方法.射影重建恢复了射影结构，还需要进一步变换得到欧氏结构，若用表示第i张影像的欧氏投影矩阵，则其必须满足：

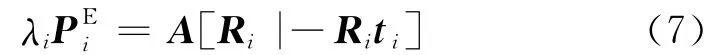
若存在一个非奇异的4×4的变换矩阵TPE可以将式（2）的射影重建转变为欧氏重建，则有：

式中，Ri为第i张影像的旋转矩阵.

取物方坐标为第一张影像的像空间坐标系，则有R1＝I，t1＝0，代入式（9），则TPE必须满足：

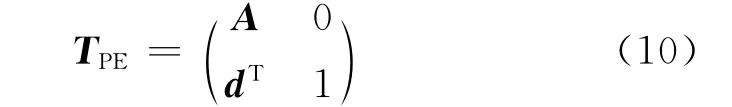
d＝（abc）T是一未知参数向量，其物理意义表示无穷远平面的法向量［2］.从射影变换到欧氏变换的工作就是利用已有的射影矩阵Pi，确定参数矩阵A、d，使所有影像均满足式（9）.

用T3表示TPE的前三列向量，pij为投影矩阵Pi的元素，代入式（9），有：

考虑旋转矩阵的正交性，将式（11）两边取转置后相乘：

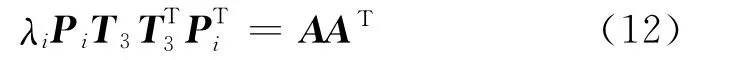
令，则式（12）可表示为

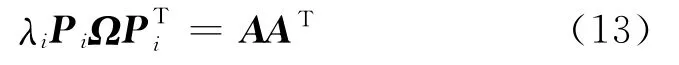
其中：

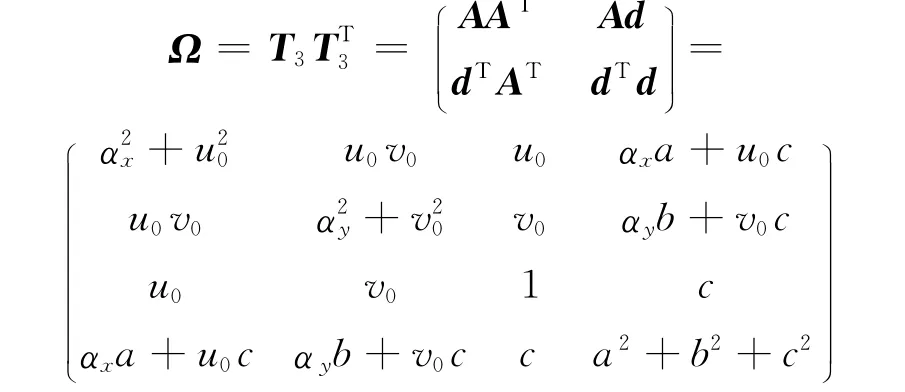
由于矩阵的对称性，每张影像按式（13）可组成6个方程，对于m个影像，未知参数为αx，αy，u0，v0，a，b，c，λi（i＝1，…，m），共有m＋7个，由于P1已经满足了式（13），因此至少需要已知两张像片的投影矩阵才能解出所有的未知参数，即共需要3张以上影像.

解算时先用线性求解参数初值，然后用最小二乘法求精，对于普通数码相机，像主点的坐标可近似选择影像中心，并将影像坐标平移至像主点位置，此时u0＝v0＝0，而绝大多数数码相机水平和垂直方向的比例系数近似相等，令αx＝αy＝α，，代入式（13），得：

不考虑各参数间的相关性，令Θ＝（α2aαbα c‖d‖21），将式（14）写成齐次方程的形式：

若共选用m张影像，则B为4（m－1）×6的矩阵，当m≥3时，可以在‖BΘ‖＝min的最小二乘准则下求解，此时Θ的值对应于矩阵B的最小特征值对应的特征向量.

以上计算没有考虑参数间的相关性，若要提高估计精度，需要用最小二乘法求精，可令目标函数F最小：

其中‖‖F表示矩阵的Frobenius范数，式（16）可以在已知参数初值的前提下采用最小二乘迭代方法，解算出内方位元素以及附加参数向量d，并进一步得到变换矩阵TPE.

3.2 外方位元素估计

通过上面的计算，恢复了内方位元素A和变换矩阵TPE，第1张影像的外方位元素已知，还需要恢复其他影像的外方位元素，对于第i（i＞1）张影像，令Q取PiTPE前三列向量，由式（9）得到：

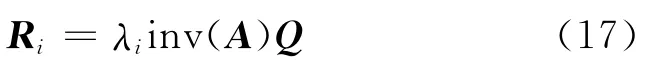
但射影重建过程中未考虑旋转矩阵的特性，并不能保证旋转矩阵满足det（Ri）＝1以及＝I的条件，可以先通过det（Ri）＝1的约束条件求出λi.

式（17）得到的Ri还未满足正交条件，需找正交矩阵＾Ri使其最接近Ri，为此将Ri进行SVD分解，设svd（Ri）＝UΣVT，则满足最小二乘‖＾Ri－Ri‖2F为最小的旋转矩阵为［12］：

4 算例

算例采用某近景摄影测量工程数据，该影像采用分辨率为1536×1024像素的Kodak DCS 420相机拍摄，拍摄过程中保持内方位元素不变，共拍摄18张照片，经光束法平差得到相机的内方位元素为：f＝1703.489，u0＝764.821，v0＝509.368，k1＝－3.79×10－8，k2＝2.60×10－14.控制点坐标用全站仪精确测量，测量精度为±1mm，选择其中的3张照片，经量测得到同名像点坐标（表1），量测精度为±0.5pixel.计算时假设主点位于影像中心，取η＝1／1000将影像坐标归一化，然后按分解算法进行射影重建，得到第2、3张影像的投影矩阵为

根据上述投影矩阵采用本文方法得到的相机内方位元素见表2，从表中可以看出内方位元素和采用传统的光束法平差结果极为接近，表明基于绝对二次曲面的自检校法能达到较高的精度.由于无物方控制，摄影基线相差一个尺度参数，将基线的X分量设为1，将得到的外方位元素和影像1－2和1－3相对定向参数比较，得到表3，可以看出差值不大，可用于确定定向参数的初值或用于低精度的近景摄影测量之中.需要指出的是，本文只选用3张影像，参与计算的像点数量和覆盖度也不太理想，若采用多张点位构形好、重叠度大的影像将有助于提高定向精度.

表1 像点的量测坐标及物方坐标Tab.1 The image coordinates and the 3Dcoordinates

表2 内方位元素及附加参数估计值Tab.2 Interior parameters and the additional unknowns estimation

表3 外方位元素值Tab.3 Exterior parameters estimation

5 结论和建议

本文采用了一种基于层次重建的近景影像定向方法，可以在无任何物方控制的条件下利用3张以上的未检校影像的同名点恢复相机的内外方位元素，是一种有别于传统摄影测量解析处理方法的新方法，但由于无物方控制和未考虑畸变，因此定向的精度相对较低，只能用于低精度的测量或作为光束法平差的初值.该方法的核心是射影重建和自检校，而自检校的精度取决于射影重建的精度，射影重建的精度除了相机本身的因素外，还与同名点的数量、分布、重叠度、量测精度等有关，因此在作业过程中要避免粗差，尽可能提高量测精度并保持较好的成像构形，否则可能导致计算失败.

［1］Heyden A，Åtrösm K.Euclidean reconstruction from constant intrinsic parameters［C］／／Proceeding International Conference of Pattern Recognition.Vienna：［s.n］，1996：339－343.

［2］Hartley R L.Self－calibration of stationary cameras［J］.Inter Journal of Computer Vision，1997，22（1）：5.

［3］Pan H P.A direct closed－form solution to general relative orientation of two stereo views［J］.Digital Signal Processing，1999，9（27）：195.

［4］Faugeras O.Stratification of 3D vision：projective，affine，and metric representations［J］.Journal of the Optical Society of America，1995，12（3）：465.

［5］Pollefeys M.Self－calibration and metric 3D reconstruction from uncalibrated image sequences ［D］.Leuven： Katholieke Universiteit.Department of Electrical Engineering，1999.

［6］邱志强，于起峰.从建筑物序列图像恢复三维结构［J］.武汉大学学报：工学版，2003，36（3）：13.QIU Zhiqiang，YU Qifeng.3D building structure from image sequences［J］.Engineering Journal of Wuhan University：Engineering Edition，2003，36（3）：13.

［7］Wang G H，Wu J.Quasi－perspective projection model：theory and application to structure and motion factorization from uncalibrated image sequences［J］.Inter Journal of Computer Vision，2010，87（3）：213.

［8］Wang G H，Wu J.Perspective 3－D euclidean reconstruction with varying camera parameters［J］.IEEE Trans on Circuits and Systems for Video Technology，2009，19（12）：1793.

［9］Tomasi C，Kanade T.Shape and motion from image stream under orthography：a factorization method［J］.International Journal of Computer Vision，1992，9（2）：137.

［10］Sturm P，Triggs B.A factorization based algorithm for multiimage projective structure and motion［C］／／Proceeding 4th European Conference on Computer Vision.［S.l.］：Springer，1996：709－720.

［11］Heyden A，Berthilsson R，Sparr G.An iterative factorization method for projective structure and motion from image sequences［J］.Image and Vision Computing，1999，17（13）：981.

［12］Zhang Z.A flexible new technique for camera calibration［J］.IEEE Trans Pattern Analysis and Machine Intelligence，2002，22（11）：1330.