Bayes估计中模糊先验信息的一类定量描述方法

张兴媛，潘洪亮，董德存

（1.同济大学 交通运输学院，上海201804；2.上海工程技术大学 航空运输学院，上海201620）

由于能够有效融合各种验前信息，近年来Bayes方法在小子样产品的可靠性评定中得到了非常广泛的应用［1－4］.尤其是在实验数据较少的情况下，运用Bayes方法，能够有效运用各种主观或客观的先验信息，以弥补现场实验数据的不足.相比较Bootstrap方法［5］，极大似然估计法等［6］，Bayes方法具有不受试验样本空间限制，同时评估结果能随新信息的出现而不断更新等优势，因此在可靠性研究中受到越来越多的关注.

使用Bayes方法的前提是先验分布的构造.通常，Bayes方法利用专家意见等先验信息的途径是将其用一个先验分布来描述，即根据先验信息按一定的方法来构造先验分布［7］.然而，当专家提供的是模糊信息时，难以有有效的方法来构造先验分布.文献［8］提出了一种Bayes分析的新思路：将试验数据视为“先验信息”，而将专家经验等先验信息视为“试验数据”，再利用Bayes公式进行统计推断.这种做法的好处是避免了在某些场合下由先验信息构造先验分布的困难，它提供了一条利用先验信息的新途径.

1 Bayes可靠性评估的思想

Bayes可靠性评估是一种基于Bayes定理的可靠性参数统计推断方法，它强调使用专家经验等先验信息以便很好地解决常规可靠性方法解决不了的小样本事件或无失效数据的可靠性评估问题.在连续随机变量的情形下，

2 可靠性评估

2.1 不精确可靠性数据的模糊描述

很多时候，专家由于自身的局限性或者对产品批次特性的难以把握，很难给出一个确切的可靠性特征量的估计值，常常会借助于模糊语言，如“产品的可靠度大约为0.95”，“失效率在某范围以内”等.对于可靠性评估过程中存在的不精确可靠性信息采用模糊理论中的模糊集合来描述.常用的隶属函数有三角形隶属函数，梯形隶属函数，矩形隶属函数以及正态隶属函数等.这四类模糊数都是根据其隶属函数的几何形状定义的.本文重点考察元件的失效率特性，所以采用三角形模糊数和正态形模糊数加以评估.

三角形模糊数的隶属函数可记作（a，b，c），其中a＜b＜c，a、c为上下限，表征模糊边界，b为极可能值，表征模糊信息的中心.三角形模糊函数记为

正态隶属函数可记为（b，σ），其中b、σ分别表示隶属函数的期望值和半宽，表示模糊信息的中心与模糊（半）宽度.正态模糊函数记为

2.2 相容性检验

先验信息是Bayes方法的基础和关键，它对最终的可靠性评估结果有着很大的影响.因此对于实验测得的样本数据作为先验信息，需对可信度进行相容性检验.在很多工程科研或试验单位常用简单的定性判别方法来说明相容性检验问题.如图比较说明法，时序模型趋时，则可认为这两个母体为同一母体，因此可以利用先验信息；否则，先验信息就不可以用.在对历史试验数据进行相容性检验时，若总体的分布函数形式己知，则可以使用参数方法进行总体相容性检验；若总体的分布函数形式未知，则适合用非参数方法进行相容性检验.常用的参数统计方法有参数的假设检验，Bayes置信区间估计等.当总体的分布函数形式未知时，可利用K－S检验、χ2检验，Wilcoxon秩和检验等.其中χ2检验虽然形式简单，然而它存在许多不足：需要较大的子样容量；划分子集（区间）受人为因素影响（如怎样划分，数目多少等）；分割子集使大量有用的信息没有得到充分利用，检验功效不高［9］.而 K－S检验也需大样本，考虑到这里样本数量较小，本文采用秩和检验.

为了检验试验数据X＝（x1，x2，…，xn1）和验前子样Y＝（y1，y2，…，yn2）是否属于同一总体，引入竞择假设

H0：X与Y属于同一总体

H1：X与Y不属于同一总体

将试验数据和验前子样两个子样混合排序（由小到大排序），可得次序统计量：

式中，vmax为粒子速度峰值，m·s-1；umax为比例粒子位移峰值，为比距离，m·kt-1/3；r为测点半径，m；Q为爆炸当量，kt TNT。

记yk＝Zj，即验前子样中的第k个元素yk，在混合排序中排列在第j位，即yk的秩为j，记为rk（y）＝j.则验前子样的秩和T为则可建立下列关系：P｛T1＜T＜T2｜H0｝＝1－α.其中α为弃真概率.给定α之下，T1，T2查秩和检验表得到.在检验水平α之下，如果T1＜T＜T2则采纳H0，即X与Y属于同一总体：如果T≤T1或T≥T2，则拒绝H0，即X与Y不属于同一总体.

2.3 模糊先验信息Bayes估计

指数分布产品的可靠性参数（失效率为λ）置信分布的推导过程如下：假设某指数产品预定失效次数为z，总试验时间为τ，则有：

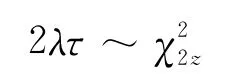
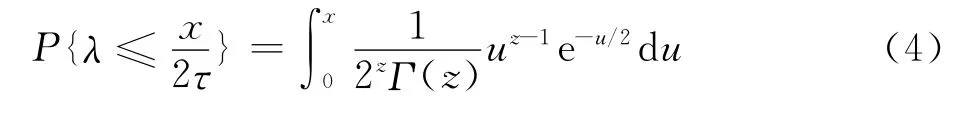
式中：Γ（z）指Γ函数（gamma函数），或写作：

如果将τ看作固定的，则式（5）规定了λ的一个分布，即：

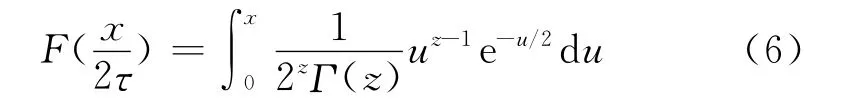
故，

式（7）即为失效率的置信分布Πb（λ），在此将其视为λ的“先验分布”.则失效率λ的密度函数为

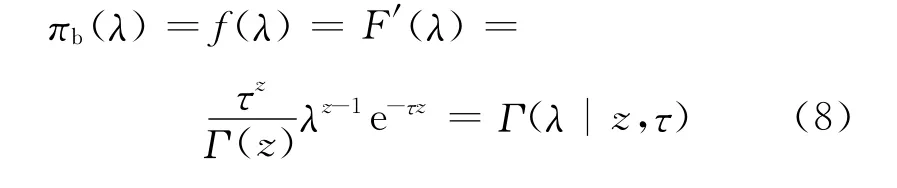
3 可靠性评估实例分析

对语音选择器组件进行了8次试验，总工作时间为15 632h；根据式（8），试验数据获取的该产品的失效率λ的置信分布为

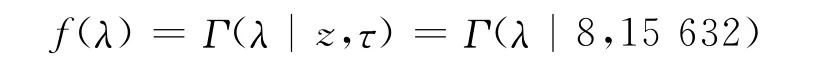
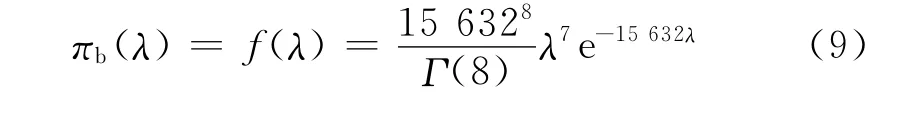
（1）可靠性专家根据自己的实践经验和实验室模拟试验的情况针对该产品的失效率λ给出的先验信息为“最可能值为0.000 56，下限、上限分别为0和0.001 5”.

① 可用三角模糊函数表示，由式（2），

将式（9）～（11）代入式（1）计算得到后验分布：

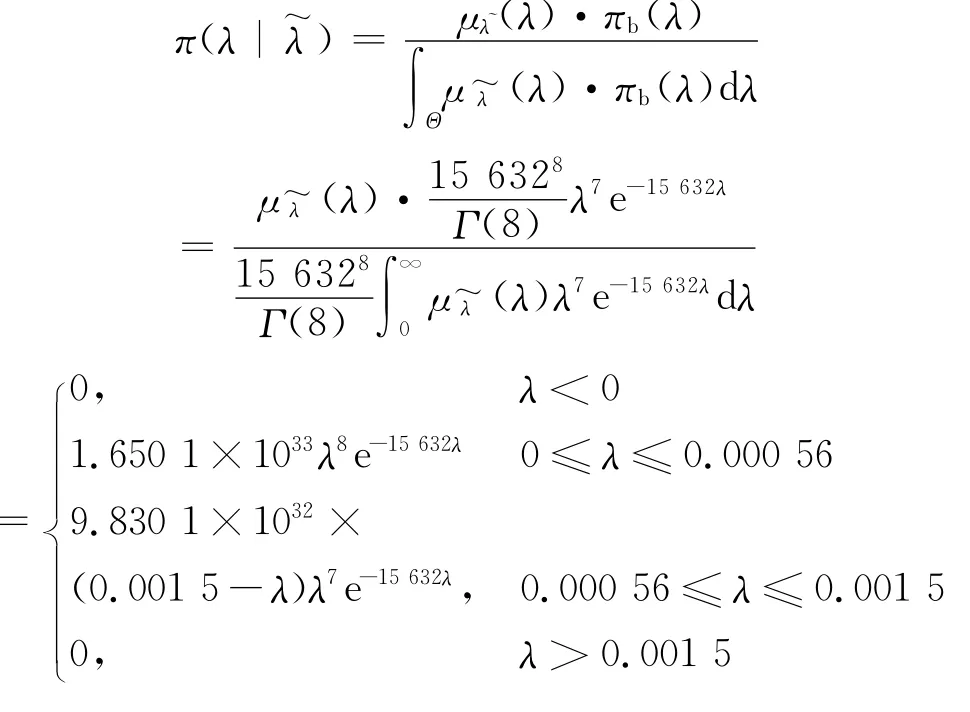
② 以a，b之差作为正态模糊先验函数的半宽，由式（2），则σ＝b－a＝0.000 56h，正态模糊先验函数为

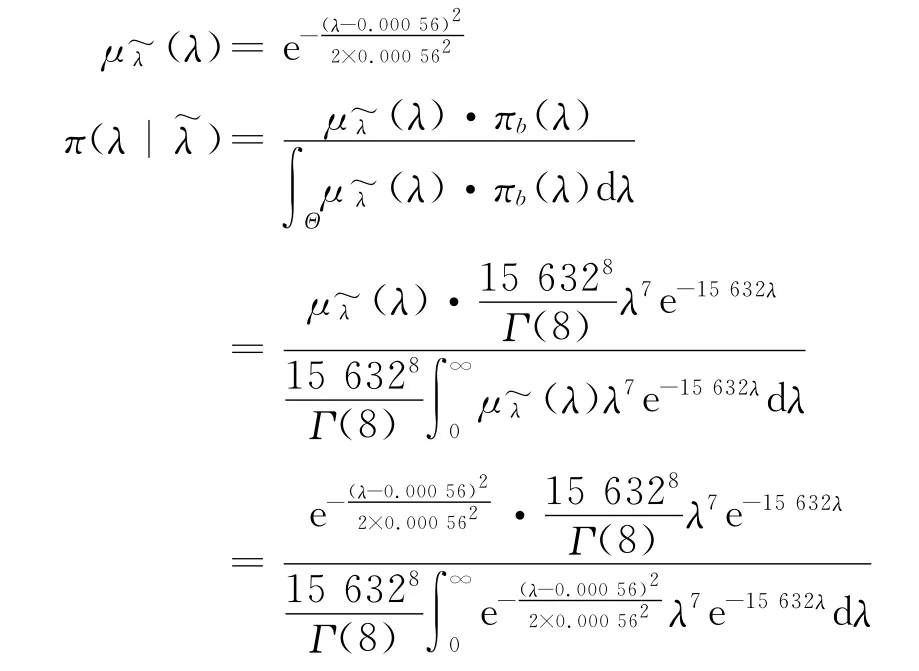
图1所示为仅根据实验数据得到的置信分布与归一化的Bayes先验分布及后验分布之间的关系（故障率—概率密度）.图中Bayes后验分布分别对应采用三角型和正态型模糊专家信息（宽带）的情况.由图1可见，在专家模糊信息分布较宽的情况下，采用三角分布的模糊专家信息具有较好的融合特性.Bayes后验分布是试验分布于专家分布的折中和融合，其峰值处于两种分布的峰值之间.并且后验分布相对于试验分布和专家信息分布置信区间宽度明显缩小，这说明Bayes估计在多说情况下能有效缩小置信区间范围，提高估计精度.而采用正态型分布的专家信息，后验分布与试验分布基本重合，专家信息没有体现.这是由于相同的置信点估计和置信区间条件下，正态分布比三角分布有更大的截尾，模糊区域更加宽泛.因此在Bayes融合中不能有效地体现.

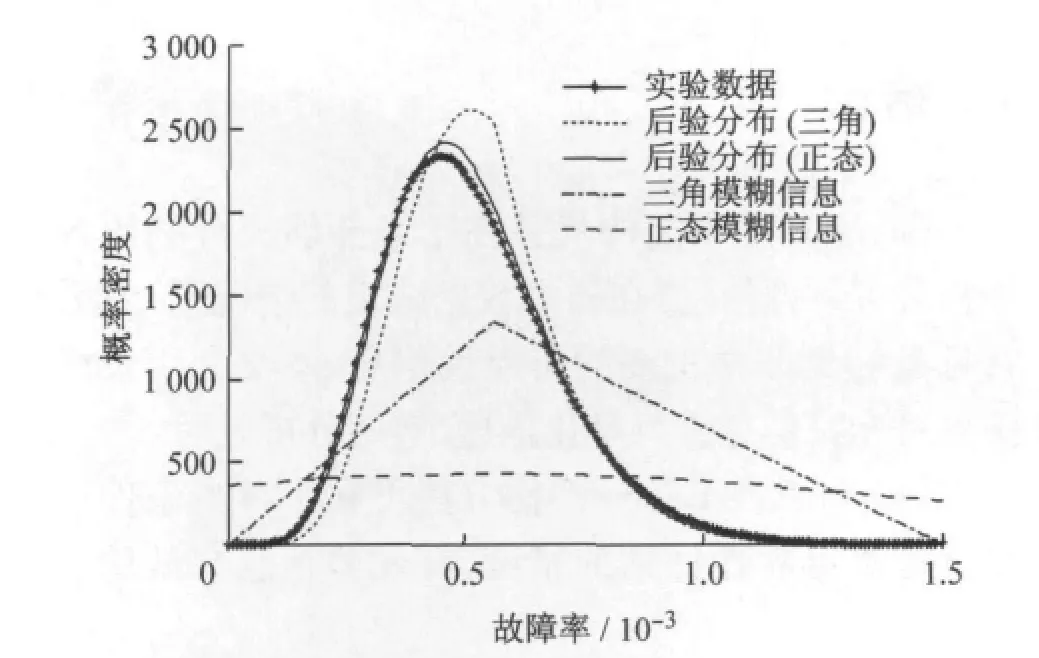
图1 专家模糊信息宽分布与Bayes后验分布之间的关系Fig.1 Relationship between narrow fuzzy prior distributions and posterior distribution

（2）模糊先验信息“最可能值为0.000 56，下限、上限分别为0.000 5和0.000 7”.可用三角模糊函数表示为：

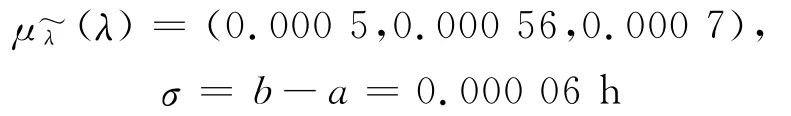
正态模糊先验函数为

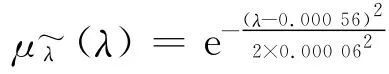
图2所示为仅根据实验数据得到的置信分布与归一化的Bayes先验分布及后验分布之间的关系（故障率—概率密度）.图中Bayes后验分布分别对应采用三角型和正态型模糊专家信息（窄带）的情况.由图2可见，在专家模糊信息分布较宽的情况下，采用正态分布的模糊专家信息具有较好的融合特性.Bayes后验分布是试验分布于专家分布的折中和融合，其峰值处于两种分布的峰值之间.采用三角模糊先验分布时，后验分布局限于先验分布的范围内，不能充分反映二者的融合.

图2 专家模糊信息窄分布与Bayes后验分布之间的关系Fig.2 Relationship between wide fuzzy prior distributions and posterior distribution

4 结论

Bayes评估方法的优势在于它能够充分利用各种相关可靠性信息.在样本数据缺乏的情况下，专家意见是一类非常重要的可靠性信息.本文利用隶属函数对专家信息进行量化描述.实例分析表明：

（1）可靠性Bayes评估方法可在小样本条件下显著提高可靠性评估的精度，在先验信息与试验信息相容的情况下，估计偏差也可以得到修正.

（2）在专家模糊信息置信区间相对试验数据较宽时，可以采用三角型隶属函数，可有效实现专家信息与试验信息的融合.而采用正态型函数时，由于带宽较宽，结果接近于无先验信息的评估.

（3）在专家模糊信息置信区间相对试验数据较窄时，可以采用正态型隶属函数，可有效实现专家信息与试验信息的融合.而采用三角型函数时，Bayes评估结果受限于专家信息的上下限，不能有效实现专家信息与试验信息的融合.

［1］Boudali H，Dugan J B.A discrete－time Bayesian network reliability modeling and analysis framework ［J］.Reliability Engineering and System Safety，2005（87）：337.

［2］Langseth H，Portinale L.Bayesian networks in reliability［J］.Reliability Engineering and System Safety，2007（92）：92.

［3］Doguc O， Ramirez－Marquez J E.A generic method for estimating system reliability using Bayesian networks ［J］.Reliability Engineering and System Safety，2009（94）：542.

［4］Montani S，Portinale L，Bobbio A，et al.A tool for reliability analysis of dynamic fault trees through conversion into dynamic Bayesian networks［J］.Reliability Engineering and System Safety，2008（93）：922.

［5］Mudelsee M，Alkio M.Quantifying effects in two－sample environmental experiments using bootstrap confidence intervals［J］.Environmental Modeling ＆Software，2007，22（1）：84.

［6］Cristiano C，Danilo M，Marco M，et al.Deterministic learning for maximum－likelihood estimation through neural networks［J］.IEEE Transactions on Neural Networks，2008，19（8）：1456.

［7］Wilson A G，Huzurbazar A V.Bayesian networks for multilevel system reliability ［J］.Reliability Engineering and System Safety，2007（92）：1413.

［8］刘晗，郭波.小子样产品可靠性Bayes评定中的相容性检验方法研究［J］.机械设计与制造，2007，5（5）：165.LIU Han，GUO Bo.Methods of compatibility test of Bayes assessment for product reliability under the circumstance of small sample［J］.Machinery Design ＆ Manufacture.2007，5（5）：165.

［9］赵永翔，杨冰，张卫华.随机疲劳长裂纹扩展率的新概率模型［J］.交通运输工程学报，2005，5（4）：6.ZHAO Yongxiang，YANG Bing，ZHANG Weihua.Probabilistic model of random－long fatigue crack propagation rates［J］.Journal of Traffic and Transportation Engineering，2005，5（4）：6.