轨道不平顺数字特征分析

梁志明，刘秀波，李红艳，李海浪

(中国铁道科学研究院 基础设施检测研究所，北京 100081)

轨道不平顺是指轨道几何位置相对轨道设计位置的变化。由于目前的测量方法无法得到轨道几何绝对位置，轨道不平顺一般由左右高低、左右轨向、水平、三角坑和轨距来描述和控制。轨道不平顺的形成和发展是很多带有随机性的因素共同作用的结果。这些因素包括钢轨的初始不平顺、线路铺设误差、道床路基的不均匀残余变形、线路维修和大修误差等。所有这些因素都使得轨道不平顺具有随机性。随机性的轨道不平顺包含许多不同幅值和波长的谐波成分，波长范围很宽，波长为0.01～200.00 m的轨道不平顺都很常见。根据国内外有关资料和专家的意见［1-5］波长1 m以下的轨面短波不平顺主要由钢轨接头、焊缝、不均匀磨耗、钢轨擦伤、剥离掉块、波浪和波纹磨耗以及轨枕间距等因素形成;波长为1～4 m的轨道不平顺主要由钢轨在轧制过程中形成的周期波和钢轨在使用中形成的波浪磨耗引起;波长为4～30 m轨道不平顺主要由道床路基的残余变形不均匀沉降、道床弹性密实度不均匀、各部件间隙不等、接头或焊缝形成的以钢轨长为基长的复杂周期波，中、小桥墩、桥台、桥头区、涵洞、道口等轨道刚度变化和桥梁动挠度等原因形成的不平顺;波长为30～200 m轨道不平顺多由道床路基沉降不均、路基施工过程中形成的先天性不平顺和跨度较大的桥梁静动挠度等原因形成的不平顺;200 m以上的轨道不平顺是由地形起伏、线路坡度变化等原因形成的。轨道不平顺的随机性决定了轨道不平顺不能用一个明确的数学表达式来表示，只能用描述随机数据的“均方值”、“标准差”、“功率谱密度”等统计函数来表示轨道不平顺的随机性特征。

以往轨道不平顺谱的计算都假设轨道不平顺具备平稳性和正态性，因此常取一段或几段线路的轨道不平顺谱表示整体轨道不平顺谱。但在轨道不平顺检测过程中发现，轨道不平顺常常具有非平稳特征。如果轨道不平顺随机数据样本是非平稳的，那么目前轨道不平顺谱的计算和统计方法就不合理。因此，对实际轨道不平顺的平稳性和正态性进行研究很有必要。

1 轨道不平顺平稳性和正态性检验方法

1.1 平稳性检验方法

最常用的方法有轮次检验［6］和逆序检验［7］，均为非参数检验。

1)轮次检验

轮次检验原理是将被分析的随机信号分成若干段，并求出各段的均方值(或者均方根值、方差、标准差等)，组成一个新时间序列。如果信号是平稳的，则新序列的变化将是随机的，而且没有趋势项。检验步骤是先求出这些均方值的中值，再逐个地将各段的均方值与中值比较，其中大于中值的均方值记为“+”，小于中值的均方值记为“－”，这种从“+”到“－”和从“－”到“+”变化的次数称为轮次数，用 r表示。一个序列的轮次数表明了同一随机变量的测量值是否独立。平稳随机过程的轮次数将满足一定的统计规律，具有如下的均值和方差

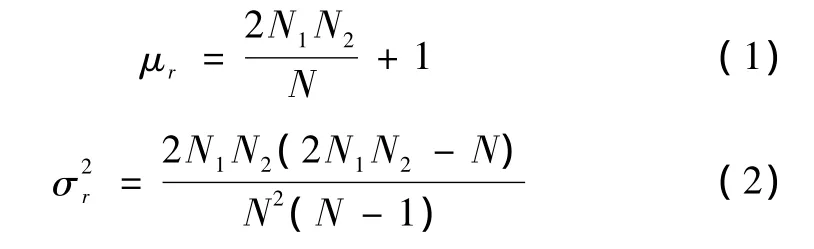
式中 N——样本记录等分段数;

N1——均值大于中值段的个数;

N2——均值小于中值段的个数;

r——轮次数。

对于平稳随机过程，当N→∞时，有 N1=N2，此时均值和方差简化为

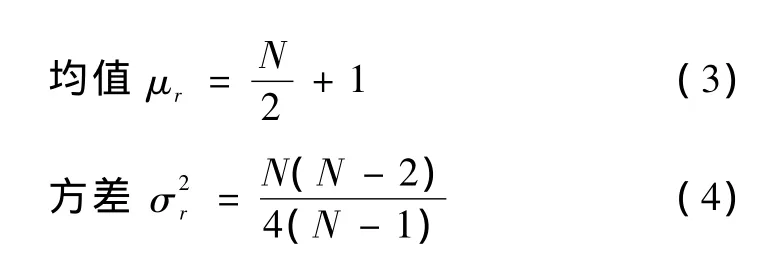
因此，式(1)是式(3)的一种逼近关系，其逼近程度与N的大小有关，在给定置信度和N的情况下，可以确定置信区间即

如果求得的轮次数r落在置信区间内，则所测量的随机过程是平稳的。落在置信区间外则是非平稳的。式(5)中的上、下限值可以由轮次查表得。

2)逆序检验

逆序检验是一种对均值或方差可能存在某种趋势进行检验的方法。首先由时间序列求出一个大致不相关的均值或方差的序列(把整个数据记录分成M段，然后求各段按时间平均的均值和方差)。设该序列为y1，y2，…，yM，每当出现 yj＞ yi(j＞ i，i=1，2，…，M －1)时，定义为yi的一个逆序。对于下标为i的已知值yi，其逆序数定义为与 yi相应的逆序的个数 Ai。逆序总数为

可以证明，以随机数序列出现的A的平均值和方差为

则统计量

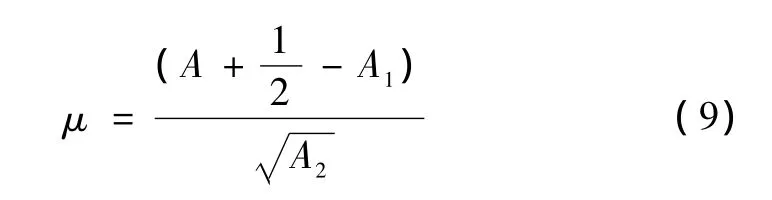
式中，A为逆序总数，A1为 A的平均值，A2为 A的方差。

渐近服从正态分布N(0，1)。根据M算出E［A］，然后按实际逆序数A得出μ值。如果μ值是处在±2之内，则可接受“序列无趋势”假设;否则拒绝该假设(在0.05显著水平上)。显然，如果 A很大，表明序列均值(或方差)有上升的趋势，而 A很小，表明序列的均值(或方差)有下降的趋势。

逆序非平稳趋势检验方法具有局限性，但对于单调的趋势随机数据序列是有效的。

1.2 正态性检验

在概率论与数理统计中，常用偏度和峰度值检验随机信号的正态性。满足正态分布随机信号的偏度和峰度近似服从正态分布。任意随机信号样本函数的偏度为S，峰度为K。可以根据下面的统计量对随机信号进行正态性检验［8］。

式中

式中，N为样本个数。

定义概率函数为

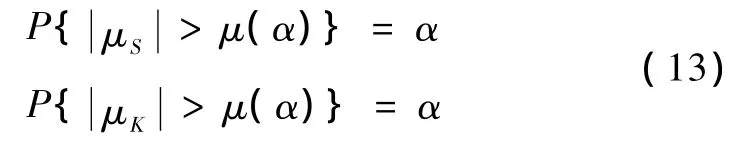
其中，α为显著水平，μ(α)可由查表得到。

根据式(10)计算随机信号样本函数的 μS和 μK，由表1，查 μ(α)则有:且，随机信号为正态分布;或，随机信号为非正态分布。

表 1 μ(α)

2 轨道不平顺统计量计算分析

2.1 轨道不平顺的平稳性

图1至图3分别为轨向、高低、轨距和水平的均方根变化曲线。从图中可以看出:如果把线路划分成不同区段，均方值变化趋势可以满足平稳性条件。这说明不同的线路条件、施工方式、维修方式、运营条件和地理环境等因素影响了轨道不平顺产生、发展和变化。线路较长时，由于线路常常划分成不同工程局施工、不同铁路局和工务段维修，使得线路设备和维修方式不尽相同，而且受不同区域地质和气候等因素影响，使得较长线路不满足平稳性条件。因此，在计算轨道不平顺谱时，不能通过局部区段轨道不平顺谱代替整条线轨道不平顺谱，而且也不能用简单平均方式计算轨道不平顺谱。

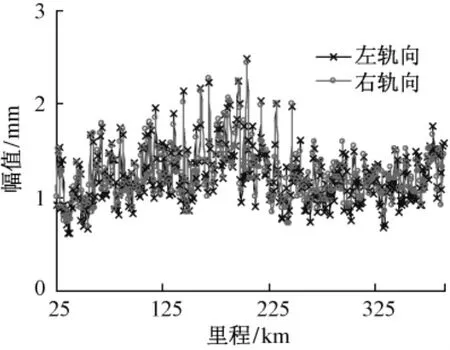
图1 轨向均方根变化曲线

图2 高低均方根变化曲线

图3 轨距和水平均方根变化曲线

2.2 轨道不平顺正态性

从图4轨道不平顺偏度变化曲线可以看出:水平不平顺偏度偏离零线较大，而且随里程变化较大，水平偏度大值主要出现在曲线头尾，而轨距偏度大值主要出现在道岔附近。

从图5轨道不平顺峰度变化曲线可以看出:轨距不平顺峰度除局部地段远大于3外，其余都接近3;水平不平顺峰度大于3。

由以上分析可知，部分里程不满足正态性。进一步研究发现，峰度大的位置一般包含幅值较大的长波局部不平顺，如图6所示线路设置的超高对水平不平顺的影响，正是这一原因使得轨道不平顺不能满足正态性，同时也表明轨道不平顺含有非平稳特征成分或趋势项。

3 结论

研究了轨道不平顺数字特征的统计量和检验轨道不平顺平稳性和正态性的方法。利用实测的轨道不平顺数据对轨道不平顺的数字特征、平稳性和正态性进行了研究。通过研究得到以下结论:

1)按1 000 m长度计算，轨道不平顺数据绝大多数里程不满足正态性条件。长波大幅值局部不平顺是产生轨道不平顺不满足正态性的主要原因。

2)线路局部区段满足平稳性条件，但整条线路基本不满足平稳性条件。

［1］ 赵国堂．高速铁路无碴轨道结构［M］．北京:中国铁道出版社，2006．

［2］ 袁长卿，高月婷．轨道不平顺性对高速铁路的影响［J］．铁道建筑，2007(增):109-112．

［3］ 陈宪麦，杨凤春，吴旺青，等．秦沈客运专线轨道谱的研究［J］．铁道建筑，2006(8):94-97．

［4］ COENRAAD ESVELD．ModernRailwayTrack(Second Edition)［M］．Holand:MRT-Productions，2001．

［5］ 杨飞，黎国清，刘金朝，等．高速铁路轨道不平顺预设试验最大幅值的研究［J］．铁道建筑，2011(7):112-115．

［6］ 刘秀波，吴卫新．钢轨焊接接头短波不平顺功率谱分析［J］．中国铁道科学，2000，21(2):26-33．

［7］ 杨位钦，顾岚．时间序列分析与动态数据建模［M］．北京:北京理工大学出版社，1988．

［8］ 中国电子、仪器仪表学会信号处理学会《振动数字信号处理程序库》编委会．振动数字信号处理程序库［M］．北京:科学出版社，1988．