有源干扰条件下机载MIMO雷达STAP协方差矩阵秩的分析
杨晓超 刘宏伟 王 勇 纠 博
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
1 引言
空时自适应处理(Space-Time Adaptive Processing, STAP)技术是机载 SIMO(Single-Input Multi-Output)雷达(即相控阵雷达)为了更好地抑制空时耦合的地杂波,检测地面动目标而提出的[1]。STAP中杂波协方差矩阵的秩,是SIMO雷达是否可以有效抑制杂波的重要指标[2]。典型的 STAP场景中,不仅包括杂波还包含有源干扰[2,3],文献[4]研究了在正侧阵时SIMO雷达杂波加有源干扰的协方差矩阵的结构,证明了杂波加干扰协方差矩阵秩的上界为两者秩之和减去有源干扰个数。一般情况下,在杂波加有源干扰协方差矩阵非满秩时,理论上SIMO雷达可以有足够的自由度来有效地抑制杂波和有源干扰,取得良好的性能。
相比于SIMO雷达,MIMO(Multi-Input Multi-Output)雷达有更多的空间自由度[5],将 MIMO 雷达用于机载平台,结合STAP技术来检测动目标成为近几年的研究热点[5-11]。文献[5]分析了发射正交波形时,机载MIMO雷达杂波子空间和杂波的秩;文献[6]和文献[7]分别分析了发射任意波形时机载MIMO雷达杂波的秩及杂波空时谱分布特性;文献[8]研究了发射相位编码正交信号和多载频信号时的MIMO雷达 STAP信号模型和杂波模型。文献[9]研究了采用频分正交信号的机载 MIMO雷达对地面动目标的角度和多普勒估计的CRB(Cramer-Rao Bound)。文献[10]对MIMO雷达进行子阵划分,然后再进行空时处理;文献[11]提出一种先时域多普勒滤波,然后再在空域采用双迭代算法进行降维的方法。
与SIMO雷达相似,MIMO雷达杂波加干扰协方差矩阵的秩也是其是否可以有效地抑制杂波和有源干扰的重要指标。文献[5]分析了MIMO雷达杂波协方差矩阵的秩,但目前还没有文献分析存在有源干扰时,MIMO雷达杂波加有源干扰协方差矩阵的秩。本文将文献[4]中SIMO雷达杂波加有源干扰协方差矩阵秩的结论推广到MIMO雷达,得到了正侧阵时 MIMO雷达杂波加有源干扰协方差矩阵秩的上界为两者秩之和减去有源干扰个数,文献[4]中的结论可以看作此结论在SIMO雷达时的特殊情况。由此结论进而得到一个有源干扰个数的范围,当有源干扰个数增加到此范围内时,SIMO雷达杂波加有源干扰协方差矩阵满秩,杂波和干扰不能被有效抑制引起性能严重下降,但此时MIMO雷达杂波加有源干扰协方差矩阵的秩要小于数据维数,MIMO雷达仍然可以有效地抑制杂波和有源干扰,有较好的理论性能,体现了MIMO雷达相对于SIMO雷达的优越性。
2 MIMO雷达STAP信号模型
考虑一个收发同置的机载MIMO雷达,发射阵有M个天线,接收阵有N个天线,都为均匀线阵,正侧阵放置。载机速度为v。目标,杂波,有源干扰相对雷达处于远场。各发射阵元发射相互正交信号,并且为窄带信号,发射脉冲重复周期为Tr。假设一个相参处理间隔(Coherent Processing Interval,CPI)共有K次脉冲。接收经过混频至基带后,用发射信号矩阵对每个接收阵元回波信号进行匹配滤波处理后排成列向量得到MN×1的输出,将K次脉冲的输出首尾相接排成更长的列向量,得到目标的输出为
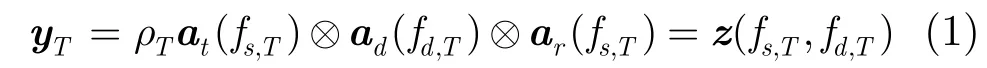
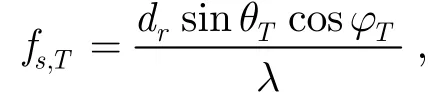

其中γ=dt/dr为发射阵元间距与接收阵元间距之比。

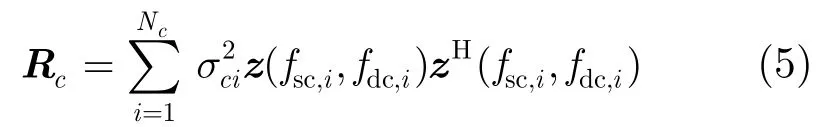
假设场景中存在J个相互独立的有源干扰,和雷达发射信号相互独立,并且在时域上各时刻之间也相互独立。其协方差阵可以表示为
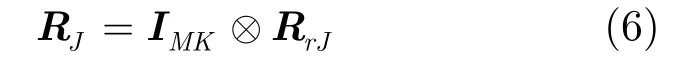

3 MIMO雷达杂波加干扰协方差矩阵秩的分析
对于正侧阵放置的SIMO雷达,在没有杂波内部运动时,由 Brennan条件[2],可以得到杂波协方差矩阵的秩rC,SIMO=rank(RC,SIMO) =N+β(K-1)。而其干扰协方差矩阵的秩为rJ,SIMO= r ank(RJ,SIMO)=JK[2]。但杂波加干扰协方差矩阵秩的上界并不等于杂波协方差矩阵的秩和干扰协方差矩阵的秩之和,文献[4]证明其上界为两者之和再减去干扰的个数,即
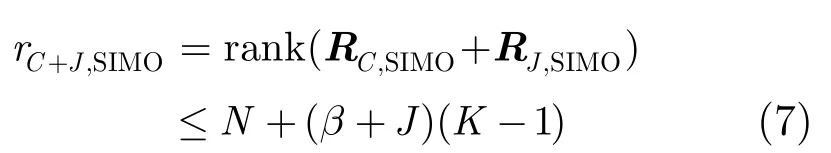
但目前还没有文献研究 MIMO雷达杂波加干扰协方差矩阵的秩,下面证明其上界为杂波协方差矩阵的秩与干扰协方差矩阵的秩之和再减去干扰的个数。
对于MIMO雷达,杂波协方差矩阵的秩为[5]

与文献[4]构造SIMO雷达杂波基向量的方法相似,可以构造MIMO雷达MKN× 1维的杂波基向量为
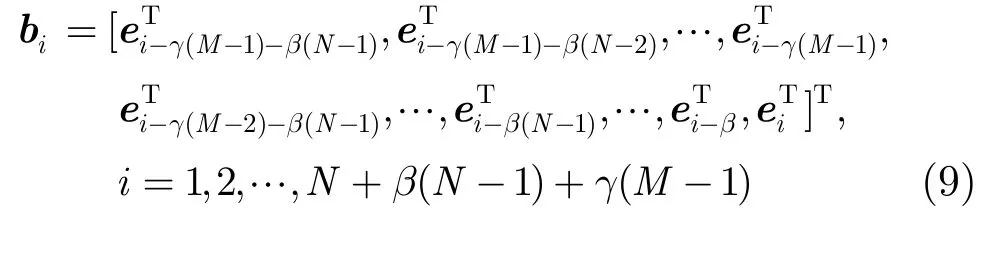

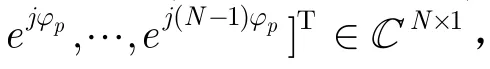

每个有源干扰对应MK个基向量,J个有源干扰一共有JMK个干扰基向量。与SIMO雷达杂波基向量和有源干扰基向量的关系[4]相似,可以验证对于MIMO雷达,第p个有源干扰的基向量和杂波的基向量有如下关系:

即第p个有源干扰的MK个基向量中至少有一个基向量可以用其他MK-1个基向量和N+β(K-1)+γ(M- 1 )个杂波基向量线性表示。对于每一个有源干扰,与其对应的基向量和杂波的基向量都有如式(11)的关系。所以,在总的有源干扰协方差矩阵的JMK个基向量中,至少有J个基向量可以由其他J(MK- 1 )个基向量和N+β(K- 1) +γ(M- 1 )个杂波基向量线性表示。由此可以得到MIMO雷达杂波加有源干扰协方差矩阵的秩满足

即 MIMO雷达杂波加有源干扰协方差矩阵秩的上界为杂波协方差矩阵的秩和有源干扰协方差矩阵的秩之和减去有源干扰的个数。
在SIMO雷达中,各发射阵元发射相同的信号,可以认为式(12)中M=1。此时式(12)与文献[4]的式(7)有相同的形式。因此,结论式(12)可以看作对文献[4]的结论式(7)的推广。
4 SIMO雷达和MIMO雷达在有源干扰条件下的性能比较
对于机载SIMO雷达,一般其收发天线共用,发射接收阵元间距相同[12]。为了在相同情况下对比SIMO雷达与MIMO雷达的性能,假设SIMO雷达与MIMO雷达均为收发阵元间距相同,即γ=1。
杂波加干扰协方差矩阵的秩,是SIMO雷达和MIMO雷达是否能够有效抑制杂波和干扰的重要指标。对于SIMO雷达,由于其协方差矩阵秩的最大值为数据维数NK,由式(7)可以得到在有源干扰个数J≥N-β时,有源干扰加杂波协方差矩阵秩的上界达到NK,此时杂波和有源干扰的抑制性能会受到很大的影响。而在有源干扰个数J=N-β-1时,有源干扰加杂波协方差矩阵秩的上界为NK-(K-1),此时SIMO雷达仍然有足够的自由度抑制杂波和干扰,性能不会有很大的下降。

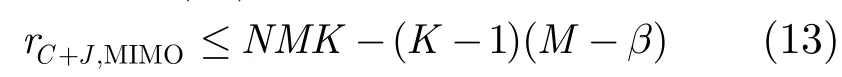
由式(13)可以看出,此时,MIMO雷达杂波加有源干扰协方差矩阵秩的上界与 MIMO雷达的数据维数NMK相差(K- 1 )(M-β),而当干扰个数J<N- 1时,与NMK相差更大,此时 MIMO雷达有足够的自由度来抑制杂波和干扰,性能不会有很大损失。所以可以得到,在干扰个数满足N-β≤J≤N- 1时,SIMO雷达的性能会有明显的下降,而 MIMO雷达的性能不会有很大的影响,显示了MIMO雷达相对于SIMO雷达的优势。
在此需要说明的是,由于有源干扰为干扰机发射的干扰信号,并非雷达发射信号的回波,所以有源干扰的抑制,不论对于SIMO雷达还是MIMO雷达,都只与接收的空间自由度有关,这也可以从MIMO 雷达有源干扰的协方差矩阵式(6)看出。而MIMO雷达相对于SIMO雷达更多的自由度来自于发射的空间自由度,并不能用来抑制有源干扰。没有杂波时,SIMO雷达和MIMO雷达抑制有源干扰的能力是相同的,最多为N-1个。但对于杂波,由于其为雷达发射信号被后向散射的回波,发射的空间自由度可以用来进行杂波抑制,由于机载雷达杂波的空时耦合性,所以机载MIMO雷达可以联合发射,接收空间自由度和时间自由度来抑制杂波,而机载SIMO雷达则只能联合接收空间自由度和时间自由度来抑制杂波。所以在杂波和有源干扰同时存在的环境中,MIMO雷达联合发射,接收自由度和时间自由度来抑制杂波,相比于SIMO雷达只能用接收自由度和时间自由度来抑制杂波,可以有更多的接收自由度来抑制有源干扰,所以在有源干扰个数增加到使得SIMO雷达性能严重下降时,MIMO雷达仍然有足够的自由度来抑制杂波和有源干扰,有较好的性能。
5 仿真实验
5.1 仿真条件
考虑一个雷达系统,发射阵元数M=5,接收阵元数N=8,发射和接收阵元间距为半波长,收发同置,正侧阵放置。一个CPI中的脉冲数K=8。载机高度9 km,目标在正侧视方向。有源干扰的方向分别 为θ1=20o,θ2=-2 0o,θ3=30o,θ4=-3 0o,θ5=40o,θ6=-4 0o,θ7=50o,且各干扰间相互独立,干噪比均为 70 dB。噪声为高斯白噪声,其协方差矩阵为单位矩阵I。
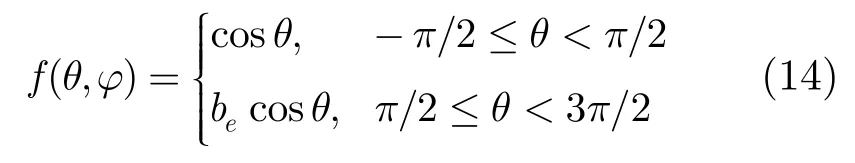
MIMO雷达与SIMO雷达仿真条件的区别仅在于发射信号的不同。对于MIMO雷达,各发射阵元发射正交信号。而SIMO雷达,各发射阵元发射相同信号,且每个阵元发射信号能量与MIMO雷达的相同,发射加权均为 1。假设每个发射阵元的阵元功率方向图相同,且均为余弦调制[12],后向衰减为60 dB,其形式如下:其中be代表后向衰减系数。对于 SIMO雷达和MIMO雷达,考虑相同的杂波背景,均为远距离杂波,每个距离环上独立杂波点个数Nc= 3 60,位置均匀分布,且同一距离单元内杂波点的RCS为独立同分布的随机变量,不同距离单元杂波点的RCS也独立同分布。下面说明对于SIMO雷达和MIMO雷达,进入单个接收阵元的单次脉冲的杂波能量是相同的。
对于SIMO雷达,单个阵元接收到的俯仰角为φ的距离单元的单次脉冲的杂波回波为

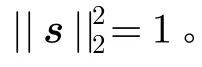

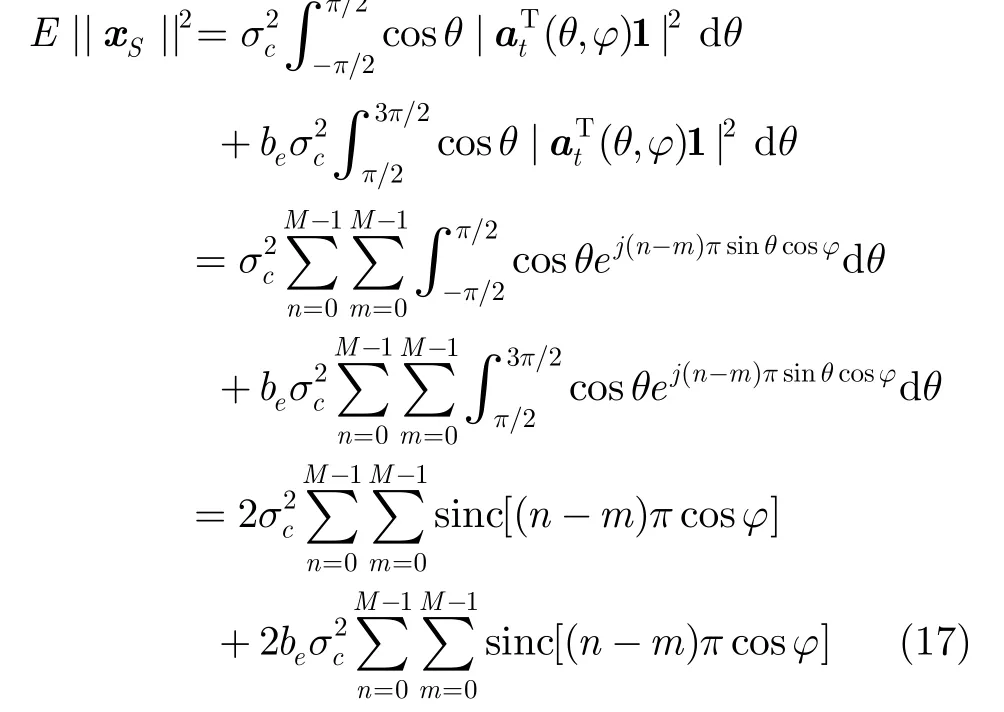
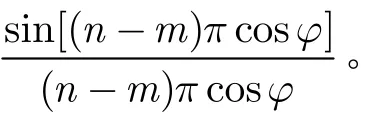

将式(18)代入式(17)可得

对于MIMO雷达,单个阵元接收到的俯仰角为φ的距离单元的单次脉冲的杂波回波为

其中S为发射信号矩阵,假设发射信号相互正交,并且满足SSH=I。此时MIMO雷达发射信号能量与SIMO的相同。由式(20)可得杂波回波的能量为

可以看出,对于SIMO雷达和MIMO雷达,单个接收阵元的单个脉冲杂波能量是相同的。在仿真中,SIMO雷达和MIMO雷达单个接收阵元的单个脉冲的杂噪比均为50 dB。
5.2 实验结果
在仿真中,采用信杂噪比(SINR)损失作为性能评价的指标。并且所用的杂波和有源干扰加噪声的协方差矩阵均为理论的协方差矩阵,不考虑有限样本数的影响。在计算SIMO雷达和MIMO雷达SINR损失时,均为全维处理,不考虑各种降维算法的影响,因此仿真中得到的SINR损失为SIMO雷达和MIMO雷达所能达到的最优性能。
图1为在β分别为1,2,3的情况下,SIMO雷达和MIMO雷达在不同有源干扰个数时的理论SINR损失。从图1(a), 1(b), 1(c)可以看出,在有源干扰数J=N-β- 1时,即分别为J=6,J=5和J=4(即分别对应β= 1 ,2,3)时,SIMO雷达的SINR损失与无干扰时的性能相差不大,在2 dB以内;但在有源干扰个数增加到J=N-β时,即分别为J=7,J= 6 和J=5(分别对应β= 1 ,2,3)时,SIMO雷达的 SINR损失在整个多普勒频率区间,性能都有了很明显的下降,尤其在低速区下降更为明显。而MIMO雷达在干扰个数J=N-β时,仍然保持了较好的性能。并且可以看出在β= 1 ,2,3的情况下,MIMO雷达在有源干扰个数为J=N- 1即7个时,其性能相比于无干扰时虽然也有了一定的下降,但下降的程度要远低于 SIMO雷达。当干扰个数从J=N-β- 1增加到J=N-β时,SIMO雷达性能严重下降,而MIMO雷达仍然有较好的性能,与本文之前的分析相一致。
为了说明当干扰个数J从N-β- 1增加到J=N-β时SIMO雷达性能下降的原因,图2 给出了SIMO雷达杂波和干扰加噪声的特征谱。由于噪声协方差矩阵为单位阵,所以杂波加干扰协方差矩阵的特征值对应于特征谱上大于0 dB的特征值,由此可得杂波加干扰协方差矩阵的秩为大于 0 dB的特征值的个数。在干扰数为J=N-β- 1,即分别为J= 6 ,J=5和J=4(分别对应β= 1 ,2,3)时,从图2可以看出,杂波加干扰协方差矩阵的秩为N+(β+J)(K- 1 ) = 5 7,而SIMO雷达全维的数据维数为64,因此有足够的自由度来抑制杂波和干扰,此时其SINR损失相对于没有干扰时没有明显的下降(见图 1)。在干扰数J=N-β,即分别为J=7,J= 6 和J=5(分别对应β= 1 ,2,3)时,杂波加干扰协方差矩阵满秩,因为所有的特征值都超过了噪声水平,其秩为64 =N+ (β+J)(K- 1 ),此时SIMO雷达没有足够的自由度来抑制干扰和杂波,所以其SINR损失有了明显的下降。
而对于MIMO雷达,从图3的杂波和干扰加噪声的特征谱上可以看出,在干扰数J=N-β,即分别为J=7,J=6和J=5(分别对应β= 1 ,2,3)时,其杂波加干扰的协方差矩阵的秩为N+β(K- 1 )+γ(M- 1 ) +J(MK- 1 ),即在β= 1 ,2,3时分别为292, 260, 228。而MIMO雷达全维的数据维数为320,所以MIMO雷达有足够的自由度来抑制杂波和干扰,仍然有较好的性能。这也体现了MIMO雷达相对于SIMO雷达可以利用更多的自由度来抑制杂波和干扰,在干扰较多严重影响SIMO雷达性能时,使得MIMO雷达还可以有效地抑制杂波和干扰,进行动目标的检测。而在干扰个数为J=N-1即7个时,MIMO雷达杂波加干扰协方差矩阵的秩在β= 1 ,2,3时分别为292, 299, 306,也与之前的分析相一致,此时MIMO雷达也有足够的自由度来抑制杂波和干扰,尽管性能相对于无干扰时会有一定的下降,但不会严重下降,不同于SIMO雷达。
6 结束语

图1 SIMO雷达和MIMO雷达SINR损失

图2 SIMO雷达杂波和干扰加噪声的特征谱

图3 MIMO雷达杂波和干扰加噪声的特征谱
将SIMO雷达杂波加有源干扰协方差阵秩的分析推广到MIMO雷达,得到MIMO雷达杂波加有源干扰协方差矩阵秩的上界为杂波秩与有源干扰秩之和减去有源干扰个数。并且得到一个有源干扰个数的范围,当有源干扰个数在此范围内时,SIMO雷达杂波加有源干扰协方差矩阵满秩,性能严重下降。而此时MIMO雷达杂波加有源干扰协方差矩阵非满秩,有足够的自由度来抑制杂波和干扰,性能没有明显的下降,显示了MIMO雷达相较于SIMO雷达的优越性。本文的分析与结论都是在比较理想的情况下得到的,可以对实际问题提供一定的参考。但本文只考虑了发射为理想正交波形的条件,对于发射为非正交波形的情况,以及如何再结合具体的情况对实际问题进行分析是下一步要进行的研究工作。
[1]Brennan L E and Reed I S. Theory of adaptive radar[J].IEEE Transactions on Aerospace and Electronic Systems,1973, 9(2): 237-252.
[2]Ward J. Space-time adaptive processing for airborne radar[R].MIT Lincoln Lab., Lexington, MA, Technical Report, 1015,1994.
[3]Klemm R. Principles of Space-Time Adaptive Processing[M].3rd Edition, London: The Institution of Engineering and Technology, 2006: 59-60.
[4]Richardson P G. STAP covariance matrix structure and its impact on clutter plus jamming suppression solutions[J].Electronics Letters, 2001, 37(2): 118-119.
[5]Chen Chun-yang and Vaidyanathan P P. MIMO radar space time adaptive processing using prolate spheroidal wave functions[J].IEEE Transactions on Signal Processing, 2008,56(2): 623-635.
[6]Wang G and Lu Y. Clutter rank of STAP in MIMO radar with waveform diversity[J].IEEE Transactions on Signal Processing, 2010, 58(2): 938-943.
[7]张西川, 谢文冲, 张永顺, 等. 任意波形相关性的机载MIMO雷达杂波建模与分析[J]. 电子与信息学报, 2011, 33(3):646-651.
Zhang Xi-chuan, Xie Wen-chong, Zhang Yong-shun,et al..Modeling and analysis of the clutter on airborne MIMO radar with arbitrary waveform correlation[J].Journal of Electronics&Information Technology, 2011, 33(3): 646-651.
[8]Wu Y, Tang J, and Peng Y N. Models and performance evaluation for multiple-input multiple-output space-time adaptive processing radar[J].IET Radar,Sonar&Navigation,2009, 3(6): 569-582.
[9]邹博, 董臻, 梁甸农. 基于STFAP的MIMO雷达运动目标参数估计的CRB研究[J]. 电子与信息学报, 2011, 33(8):1988-1992.
Zou Bo, Dong Zhen, and Liang Dian-nong. Research on CRB for moving target parameter estimation in MIMO radar based on STFAP[J].Journal of Electronics&Information Technology, 2011, 33(8): 1988-1992.
[10]李彩彩, 廖桂生, 朱圣棋, 等. MIMO雷达子阵级m-Capon 方法研究[J]. 系统工程与电子技术, 2010, 32(6): 1117-1120.
Li Cai-cai, Liao Gui-sheng, Zhu Sheng-qi,et al.. Study of subarray domain m-Capon method for MIMO radar[J].Systems Engineering and Electronics, 2010, 32(6): 1117-1120.
[11]吕晖, 冯大政, 和洁, 等. 机载MIMO雷达两级降维杂波抑制方法[J]. 电子与信息学报, 2011, 33(4): 805-809.
Lü Hui, Feng Da-zheng, He Jie,et al.. Two-stage reduceddimension clutter suppression method for airborne MIMO radar[J].Journal of Electronics&Information Technology,2011, 33(4): 805-809.
[12]Skolnik M I. Radar Handbook[M]. 2nd Edition, Boston:McGraw-Hill, 1990.

