基于软输出固定复杂度球形译码的高效迭代检测算法

沈 弘 赵春明

(东南大学移动通信国家重点实验室 南京 210096)

1 引言

多输入多输出(MIMO)技术可以在不增加发射功率和带宽的前提下显著提高无线信道容量，已成为长期演进方案(LTE)等通信标准的物理层关键技术之一。空分复用是MIMO技术的一种重要形式，其基本思想是将多天线信道分解为多个独立的并行子信道，通过在这些子信道上发送不同的数据流提高传输速率。由于空分复用系统会引入数据流之间的干扰，因而在接收端需要通过MIMO检测算法去除空域上的干扰，恢复发送数据流。目前文献中已经提出各种MIMO检测算法，其中迭代检测[1-4]是一种能够有效逼近MIMO信道容量的方案。最大后验概率(MAP)检测是最优的迭代检测算法，该方法需要遍历整个发送向量空间，因而在采用高阶调制或者数据流数较多的情况下，其复杂度非常高以至于难以实现。针对这个问题，文献[1]提出一种低复杂度的基于最小均方误差(MMSE)的软干扰抵消算法，但是其性能与 MAP检测相比有一定的差距；文献[3]对传统的硬输出球形译码(SD)算法进行改进，提出一种列表球形译码(LSD)迭代检测算法，该算法的性能虽然接近 MAP检测，但是其复杂度会随着噪声强度和信道条件的变化而改变，尤其在低信噪比或者信道条件差的情况下，复杂度仍然很高，因而不利于ASIC实现。文献[4]则在非迭代硬输出 M 算法[5]基础上提出一种迭代树搜索算法(ITS)，其优点是计算复杂度恒定，然而当采用高阶调制时，该算法仍需要较多的排序运算，并且某些比特的软输出值需要预先设定，导致性能上的损失。最近，文献[6,7]针对硬输出SD算法复杂度变化的缺点，提出一种固定复杂度球形译码(FSD)算法，该算法能以较低的复杂度获得近似硬输出 SD算法的性能，且不需要排序运算，适合ASIC实现。文献[8]提出实数域上的FSD算法，有效降低了高阶MIMO系统(如8×8)的检测复杂度。在FSD的基础上，文献[9]又提出一种软输出FSD(SFSD)算法，该方法通过比特翻转和路径添加两个步骤产生较高精度的软量。然而，SFSD算法并没有利用译码器反馈的先验信息更新检测器的软输出，因而其性能与 MAP迭代检测算法相比仍有很大差距，另外，它的预处理复杂度较大，需要多次求解矩阵的逆。

本文首先将SFSD算法推广到迭代检测中，使得其能够有效利用译码器反馈的软信息，并利用多级比特映射星座图[4]的特性大大减少分支度量的计算次数，之后又将检测顺序调整和QR分解这两个预处理步骤进行结合，在降低计算量的同时保证性能损失很小。最终的仿真结果表明，本文提出的算法能够达到近似 MAP的性能，并且复杂度远远低于MAP。

2 系统模型

图 1给出了采用迭代接收机的 MIMO系统框图。信息比特序列首先经过信道编码器和交织器，由此产生的比特序列再被映射为符号序列(假设共有Q= 2q个星座符号，q为调制阶数)，然后经过串并转换分为NT个子数据流，并从不同的天线上发射。接收端信号为

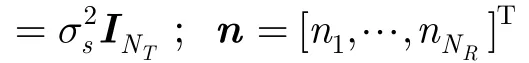
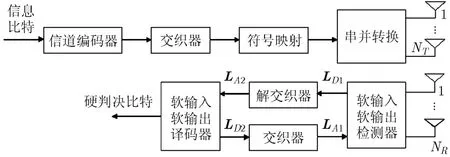
图1 MIMO迭代接收机系统框图

最优的软输入软输出检测算法是 MAP算法，其输出软量可采用Max-log近似得到[3]。

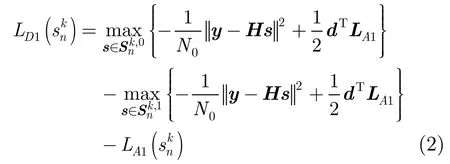
其中表示符号sn的第k个比特，分别表示满足和的发送符号向量集合。由于MAP算法需要计算次，因此当数据流数较多或者调制阶数较高时，复杂度会变得非常高。对于多输入多输出-正交频分复用(MIMOOFDM)系统，由于不同子载波的检测是独立进行的，因而本节介绍的迭代接收方案可以在 MIMOOFDM系统每个子载波上直接使用。

3 FSD和SFSD算法原理

FSD算法本质上是一种基于宽度优先原则的树形检测算法。对于前P层数据流，该算法采用遍历搜索的方法，而对后NT-P层数据流则只保留一条局部最优路径。当P满足(NR-NT)(P+ 1 ) + (P+ 1 )2≥NR时，FSD算法的性能与SD算法几乎一致(与非迭代MAP算法的性能也十分接近)。下面将介绍FSD算法的具体步骤。该算法首先通过以下步骤确定检测顺序并置换信道矩阵H的列向量：

(1)令i=1,H1=H,T1={1,2,…,NT}。

(3)交换H第Ti(ki)和NT-i+ 1列；删除Hi第ki列得Hi+1；删除Ti第ki个元素得Ti+1。

(4)如果i=NT- 1，则此时Hi+1只包含一列，Ti+1只剩余一个元素，表示已经完成检测顺序的调整；否则i的值增加 1，并跳转回(2)进入下一轮循环。

将按照上述步骤得到的信道矩阵记作，则接收信号可以写为

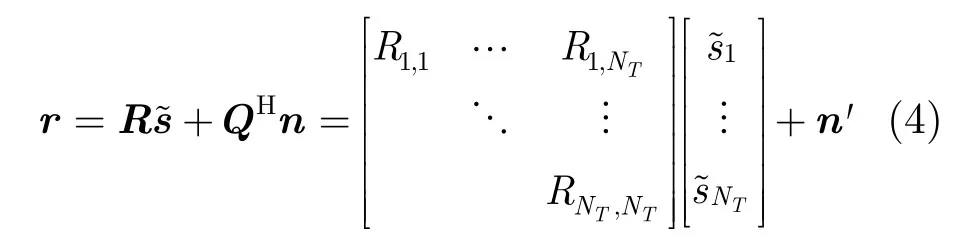
其中n'和n同分布。根据式(4)可定义符号i(i=NT,… ,1 )对应分支度量ui和路径度量wi为

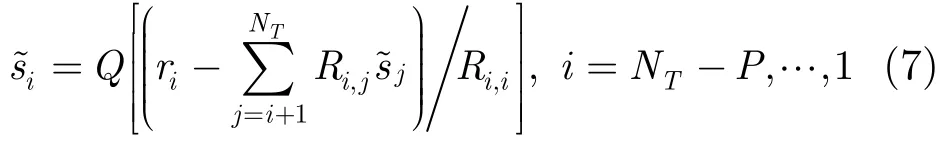
其中Q[·]表示星座图上的硬判决运算。将最终产生的路径集合记作LFSD，则硬判决输出为总路径度量值最小的路径：

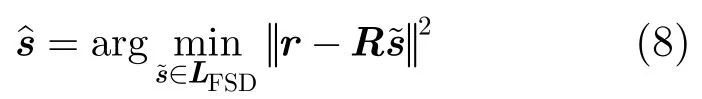
由于FSD算法只遍历前P层，使得有些路径上某些比特位只有0或1，不利于计算输出软量。SFSD算法在LFSD的基础上添加路径，保证所有比特位软量都可以计算，过程如下：

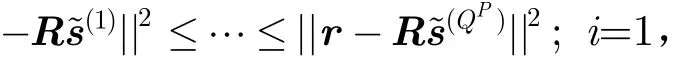
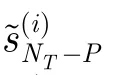
(3)如果i=NSFSD，则结束SFSD算法的树搜索过程，否则跳转回上一步。

用LSFSD表示 SFSD 算法产生的路径集合(包括FSD算法产生的QP条路径)，则最终的比特软量可以采用如下公式计算：

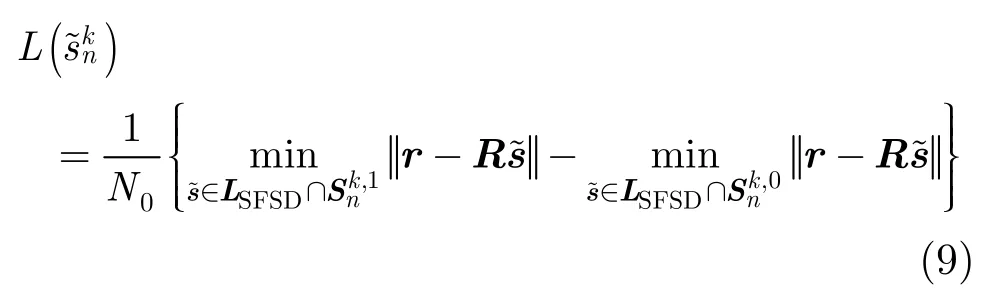
其中表示符号的第k个比特。这里我们采用欧几里德范数计算软量，可以有效地提高软量精度，该方法最早在文献[10]中提出。

文献[6,7]通过理论分析和仿真指出硬输出 FSD算法能以很低的复杂度获得近似最优硬输出的性能，其根本原因是FSD能根据不同数据流信噪比自适应的调整搜索方式。文献[9]则指出，SFSD 算法在FSD产生的符号向量集合基础上，通过比特翻转和添加路径两个步骤得到一个新的集合LSFSD，第一可以保证集合LSFSD中不会发生某个比特位只存在‘0’或者‘1’的情况，第二能确保新增加的符号向量与近似最优的＾sFSD尽可能地接近，从而使得检测器输出的软量十分精确且接近于最优软输出。

4 基于SFSD算法的迭代检测算法

SFSD算法虽然能产生较高精度软量，但是并没有利用译码器先验信息，因而不能获得迭代增益，此外该算法预处理需要较多的运算量。本文将针对这两个问题分别进行改进。

4.1 软输入软输出的SFSD算法

当检测器先验信息LA1≠0时，分支度量ui和路径度量wi需考虑LA1的作用，定义如下：

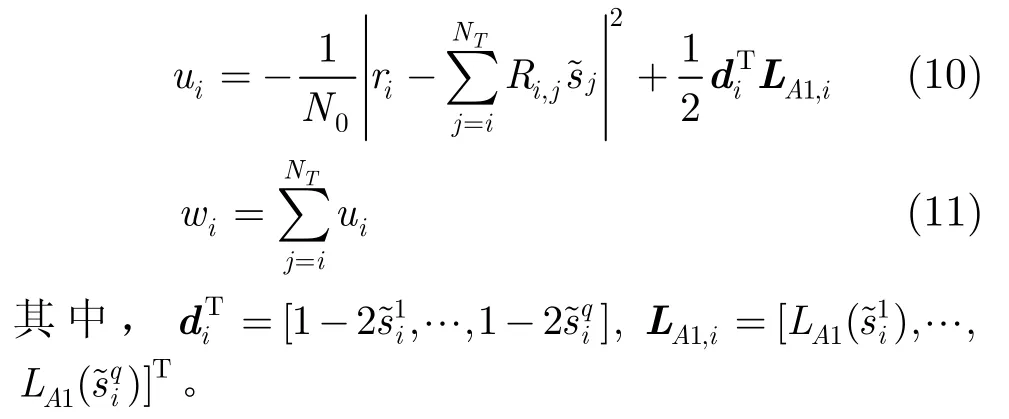
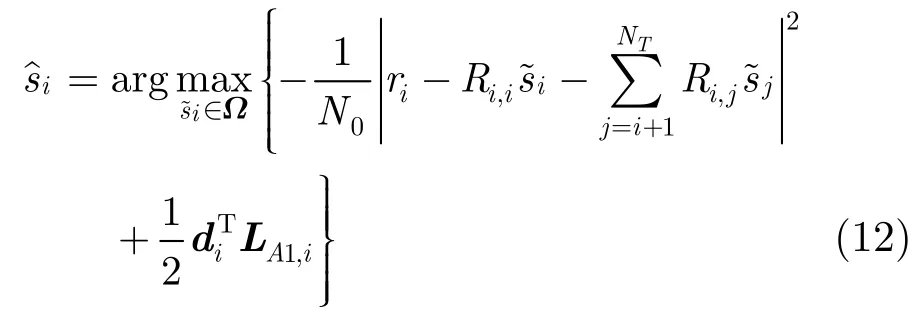
其中Ω是星座符号集合。本文提出的迭代SFSD算法在搜索发送符号向量集合时使用的方法和非迭代SFSD算法是一致的，包括FSD算法、比特翻转以及路径添加3部分。与SFSD算法的区别在于重新定义了计算软量时使用的路径度量和分支度量。根据之前对SFSD算法的分析可以推断，迭代SFSD算法同样能产生十分精确的软量，并且由于有效地利用译码器反馈的信息，其性能接近于 MAP迭代检测，事实上仿真结果也验证了这一结论。

将式(12)与式(7)进行对比可以发现，由于引入了先验信息，此时无法采用简单的符号硬判决运算，这就导致对于调制阶数较高的情况(如16QAM)，需要计算很多次分支度量值，显然对于实现是不利的。文献[4]利用多级比特映射星座图的特性，有效地简化了迭代树搜索算法中的度量计算，下面将采用文献[4]中的方法降低式(12)的计算复杂度。

图2中的实心圆表示采用多级比特映射的16 QAM 星座图，其中每个星座符号都用 4个比特表示。所谓多级比特映射的含义是：前两个比特代表了该符号所在的象限，例如“00”表示第1象限；而后两个比特则确定了该符号在象限中的位置，这样只需要两步搜索即可确定符号的具体位置(对于64 QAM 星座图则需要 3步搜索)。下面仍以 16 QAM 为例介绍如何利用多级比特映射减少搜索局部最优路径的运算量。图2中的空心圆表示每个象限内星座符号的中心，记作sC1,sC2,sC3,sC4。首先将这4个符号值分别代入式(10)计算分支度量：

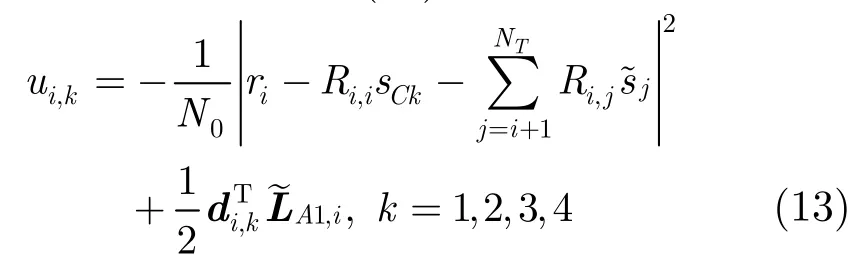
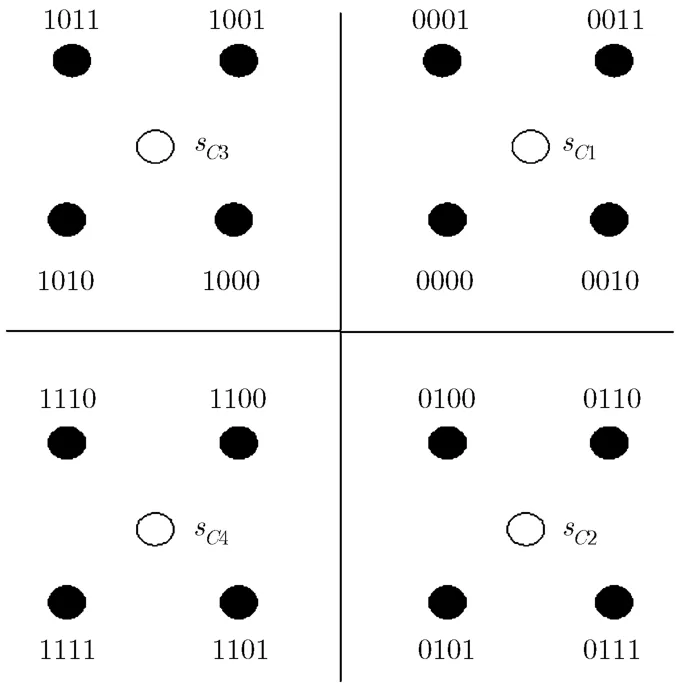
图2 多级比特映射的16 QAM星座图

4.2 简化的预处理步骤

SFSD算法的预处理包括调整检测顺序和 QR分解这两个步骤，其中调整检测顺序需要NT-1次矩阵求逆运算，当数据流较多时计算量很大。事实上，SFSD算法对最后NT-P层数据流的检测顺序调整和 V-BLAST检测[11]一致，即首先检测信噪比最高的数据流。为避免V-BLAST算法的矩阵求逆运算，文献[12]曾提出一种 SQRD检测方法，其基本思想是在QR分解同时确定检测顺序。下面我们将该方法推广到SFSD算法预处理中，具体步骤如下：

(1)令i= 1 ,H1=H,S=T1={1 ,2,… ,NT}。

(3)交换H的第Ti(ki)列和第NT-i+ 1列；交换S的第Ti(ki)个元素和第NT-i+ 1个元素；删除Hi的第ki列，得到Hi+1；删除Ti的第ki个元素，得到Ti+1。如果i=P，则进行下一步操作，否则i增加1并跳转回上一步。

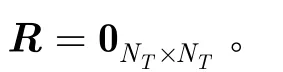
(5)当i≤NT-P时，按照式(14)求解ki：

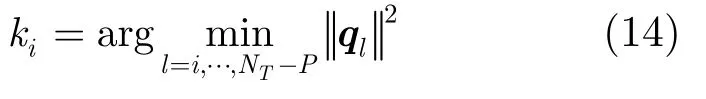
其中ql表示Q的第l列；分别交换Q和R的第i和ki列，交换S的第i和ki个元素。

(6)采用Gram-Schmidt正交化方法更新矩阵Q和R，包括以下几步：

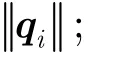
(b)qi=qi/ri,i;

(c)ri,l=qiHql,ql=ql-ri,lqi,l=i+ 1,… ,NT。

(7)如果i=NT，则完成预处理，否则i增加1并跳转回(5)。

该简化方法保证前P层数据流的检测顺序和SFSD算法相同，而后面NT-P层数据流的检测顺序则由SQRD算法确定，和原来的预处理方法相比，不但可以省去NT-P- 1次矩阵求逆，而且性能损失很小。这主要是因为SQRD算法能保证QR分解后得到的上三角阵R满足如下性质：较小的对角元在左上方而较大的对角元在右下方，又由于较大对角元对应的数据流具有较高的信噪比[12]，因而信噪比较大数据流可以先被检测。虽然这种检测顺序调整方式不完全等价于下文算法 1中多次求逆的方法，但基本思想是一致的，即减少误差传播影响。

5 算法性能仿真

本节将给出LTE下行链路环境中不同算法的性能，表1列出了仿真中采用的系统参数。

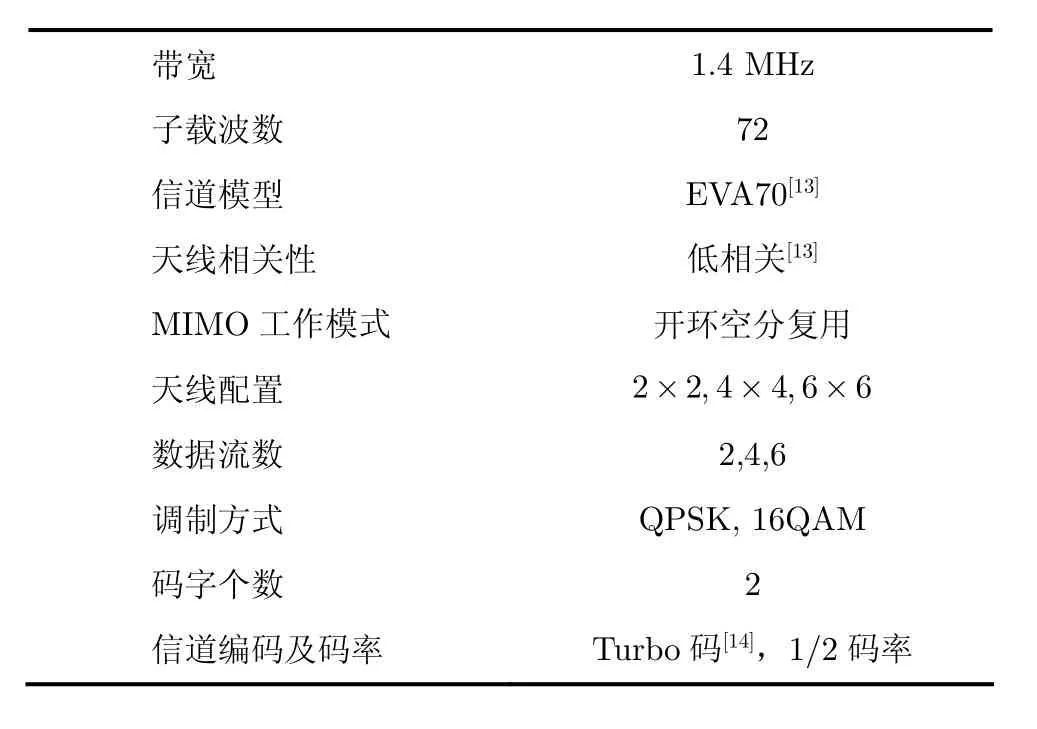
表1 LTE下行链路仿真参数

考虑 LTE下行链路中3种天线配置：2×2, 4×4和6×6。通过仿真发现3种天线配置下较为理想的NSFSD分别为1, 3和6。下文“基于SFSD的迭代算法1”是利用式(12)寻找每层局部最优路径，并采用原始SFSD算法的预处理；“基于SFSD的迭代算法 2”是在算法 1基础上，利用多级比特映射星座图特性减少分支度量计算并对简化预处理。

图3比较了2×2MIMO, 16QAM调制情况下两种基于SFSD的迭代算法误帧率性能。从图中可以看到，基于SFSD的迭代算法2和算法1的性能几乎无区别，这表明算法2采用的简化是合理的。此外两种基于SFSD的迭代算法在第1次迭代时能获得0.5 dB性能增益(误帧率0.1)，第2次迭代时增益变小，说明迭代趋于收敛。与 MAP算法相比，不进行迭代时基于SFSD的迭代算法2约有0.2 dB的损失(误帧率0.1)，而对于迭代一次和两次则几乎无损失。

图4比较了4×4MIMO, 16QAM调制情况下两种基于SFSD的迭代算法性能。从图中可以看到，基于SFSD的迭代算法2的误帧率十分接近算法1，这表明算法2的简化处理对性能影响很小。此外，两种基于SFSD的迭代算法在第1次迭代时即可获得0.7 dB的增益(误帧率0.1)，第2次迭代获得增益变小，说明迭代趋于收敛。与 MAP算法相比，不进行迭代时基于SFSD的迭代算法2约有0.25 dB的性能损失(误帧率 0.1)，迭代 1次时损失为 0.1 dB(误帧率0.1)。当迭代次数为2时损失变得更小。

图5比较了6×6MIMO, QPSK调制情况下两种基于SFSD的迭代算法与MAP算法的性能。从结果中可以看到，基于SFSD的迭代算法2的误帧率十分接近算法1，这表明即使在高阶MIMO情况下，算法2的简化处理也是有效的。在不进行迭代时基于SFSD的迭代算法2相对于MAP算法约有0.25 dB的性能损失(误帧率0.1)，而迭代1次时，性能损失则减小为0.1 dB(误帧率0.1)，两次迭代情况下损失变得很小。

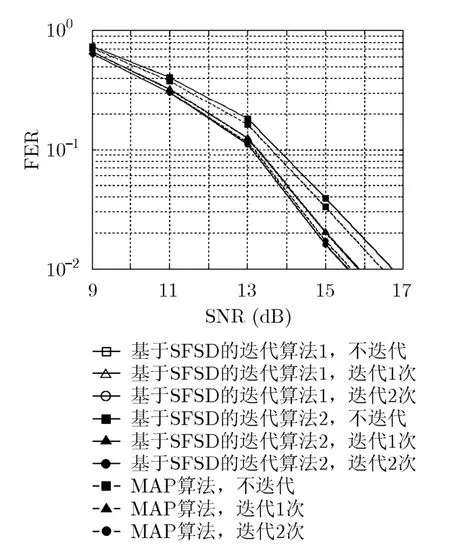
图3 基于SFSD的迭代算法性能(N T =N R = 2 , 16QAM调制)

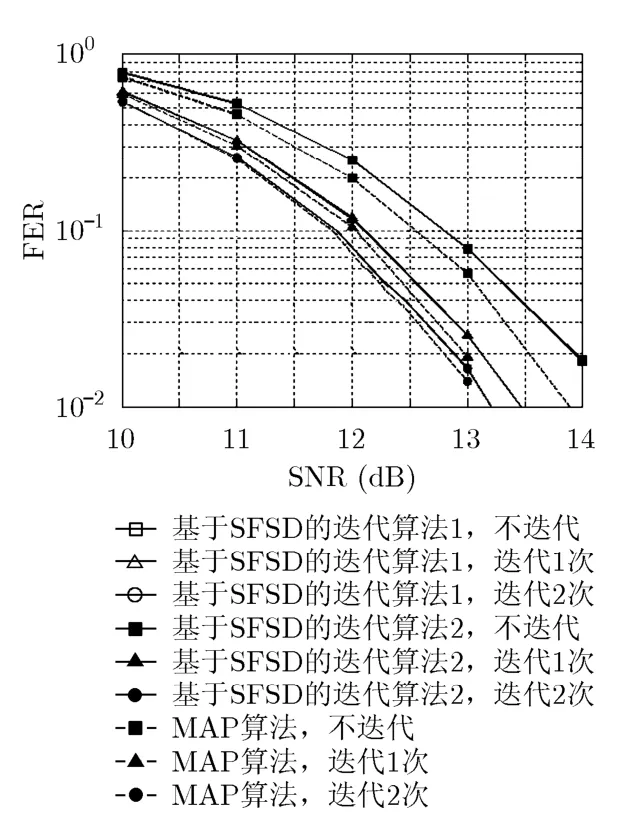
图4 基于SFSD的迭代算法性能 ( N T =N R = 4 , 16QAM调制)

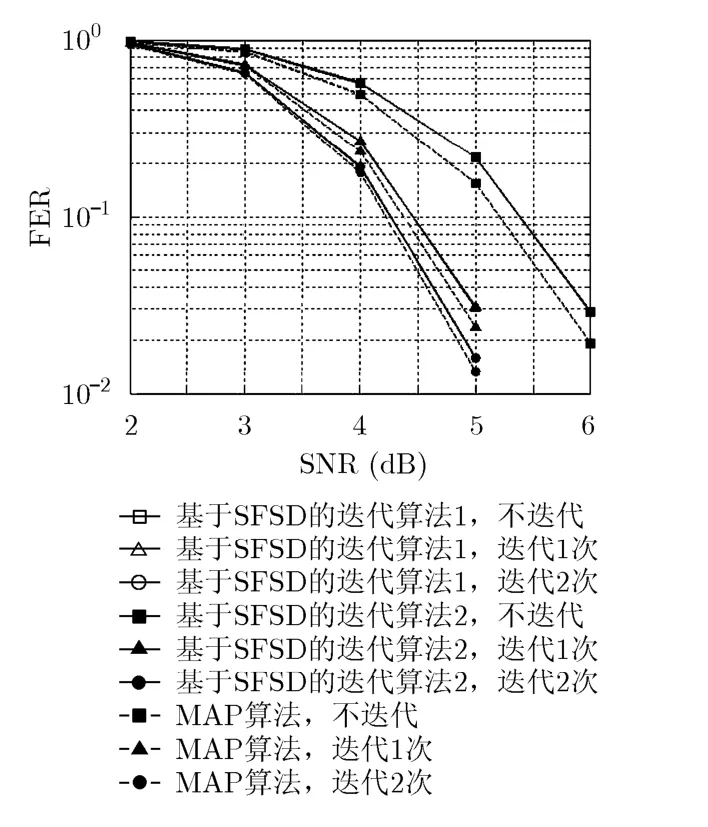
图5 基于SFSD的迭代算法与MAP算法性能比较( N T =N R = 6 , QPSK调制)

表2列出了MAP检测和两种基于SFSD的迭代算法的计算复杂度(单个子载波)。从表中可以发现，在2×2MIMO, 16QAM调制下，基于SFSD的迭代算法1计算量相对于MAP算法没有显著的减少，而算法2的计算量相对于算法1有明显下降，需要实数乘法数和实数加法数约为 MAP算法的1/2和1/3。在4×4MIMO, 16 QAM调制下，基于SFSD的迭代算法 1和算法 2的计算量均远小于MAP算法，且算法2复杂度最低。对于6×6 MIMO,QPSK调制，两种基于SFSD迭代算法计算量远小于MAP算法，且算法2具有更低复杂度。

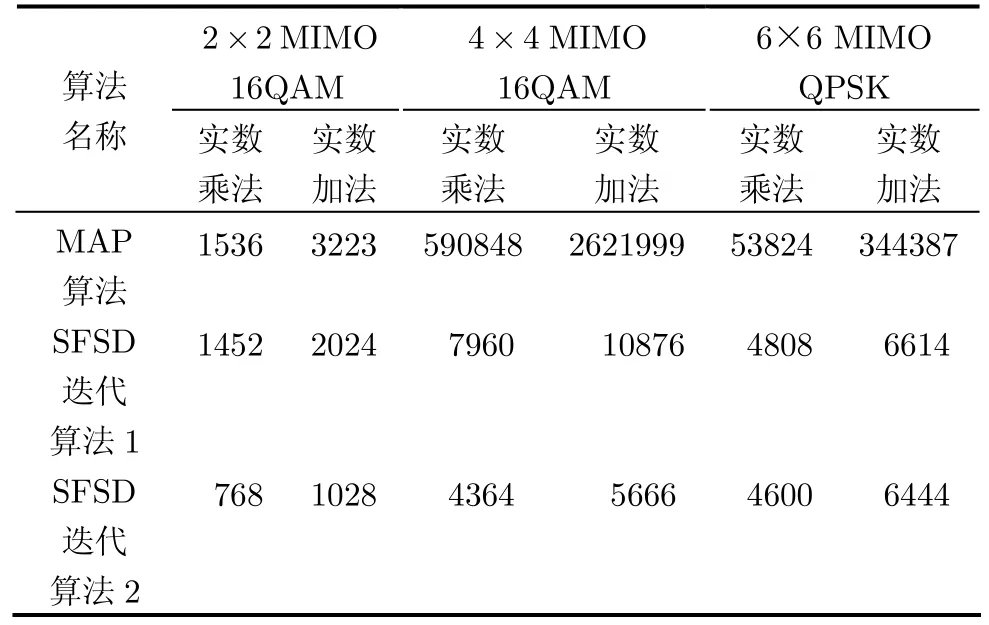
表2 算法复杂度比较(单个子载波)

6 结束语

本文提出了一种基于SFSD算法的MIMO迭代检测方案。该方法首先将译码器反馈的先验信息引入分支度量和路径度量的定义中，使得检测器软输出的精度在每次迭代过程中不断增加，获得明显的迭代增益。之后，该方案又利用多级比特映射星座图的特点，大大减少分支度量的计算次数。另外，本文还将调整检测顺序和QR分解两步相结合，减少了SFSD算法预处理中的矩阵求逆次数。在LTE下行链路环境中的仿真结果表明，本文的算法能够获得近似 MAP算法的性能，并且复杂度远低于MAP。另外本文提出的算法同样适用于调制阶数更高(如64QAM)的情况，也可以应用于发送数据流更多的MIMO系统。

[1]Sellathurai M and Haykin S. Turbo-BLAST for wireless communications: theory and experiments [J].IEEE Transactions on Signal Processing, 2002, 50(10): 2538-2546.

[2]Haykin S, Sellathurai M, De Jong Y,et al.. Turbo-MIMO for wireless communications [J].IEEE Communications Magazine, 2004, 42(10): 48-53.

[3]Hochwald B M and Ten Brink S. Achieving near-capacity on a multiple-antenna channel [J].IEEE Transactions on Communications, 2003, 51(3): 389-399.

[4]de Jong Y and Willink T J. Iterative tree search detection for MIMO wireless systems [J].IEEE Transactions on Communications,2005, 53(6): 930-935.

[5]Yue J, Kim K J, Gibson J D,et al.. Channel estimation and data detection for MIMO-OFDM systems [C]. Proceedings of IEEE GLOBECOM, San Francisco, USA, Dec. 2003:581-585.

[6]Barbero L G and Thompson J S. Fixing the complexity of the sphere decoder for MIMO detection [J].IEEE Transactions on Wireless Communications, 2008, 7(6): 2131-2142.

[7]Jaldén J, Barbero L G, Ottersten B,et al.. The error probability of the fixed-complexity sphere decoder [J].IEEE Transactions on Signal Processing, 2009, 57(7): 2711-2720.

[8]Zheng C, Chu X, McAllister J,et al.. Real-valued fixed-complexity sphere decoder for high dimensional QAM-MIMO systems [J].IEEE Transactions on Signal Processing, 2011, 59(9): 4493-4499.

[9]Barbero L G, Ratnarajah T, and Cowan C. A low-complexity soft MIMO detector based on the fixed-complexity sphere decoder [C]. Proceedings of IEEE ICASSP, Las Vegas, USA,March 2008: 2669-2672.

[10]Kawai H, Higuchi K, Maeda N,et al.. Likelihood function for QRM-MLD suitable for soft-decision Turbo decoding and its performance for OFCDM MIMO multiplexing in multipath fading channel [J].IEICE Transactions on Communications,2005, E88-B(1): 47-57.

[11]Foschini G J. Layered space-time architecture for wireless communication in a fading environment when using multiple antennas[J].Bell Labs Technical Journal, 1996, 1(2): 41-59.

[12]Wübben D, Böhnke R, Rinas J,et al.. Efficient algorithm for decoding layered space-time codes[J].Electronics Letters,2001, 37(22): 1348-1350.

[13]3GPP TSG-RAN, TS 36.101 v9.8.0. User Equipment (UE)radio transmission and reception (Release 9) [S]. 2011.

[14]3GPP TSG-RAN, TS 36.212 v9.3.0. Multiplexing and channel coding (Release 9)[S]. 2010.