阈算术代数系统及多值电流型CMOS电路设计

姚茂群 张官志 施锦河

①(杭州师范大学信息科学与工程学院 杭州 310018)

②(浙江大学信息与电子工程学系 杭州 310027)

1 引言

随着大规模集成电路的发展，人们对低电压、低功耗电路的设计要求更加迫切[1-4]。电流型电路以其具有高速度、宽带宽、失真小等优点，一直受到国际学术界的关注[4,5]，尤其在实现多值逻辑特别是高基值逻辑电路方面，电流型电路比电压型电路具有明显的优势[4-6]。多值逻辑电路由于提高了电路信息密度，减少了输入输出的引线数，一直得到国际上学者的重视[7,8]。

电流信号易于实现加法、减法、倍乘等算术运算，若能以算术运算形式表示电流型电路逻辑关系，将有助于电流型电路设计的简化[9,10]。然而，现有的逻辑电路代数系统主要以与、或、非运算为基本运算构成，更适于电压型电路的设计实现，如布尔代数系统与格代数系统。模代数系统中引入了模加法运算及模乘法运算，有利于电流型电路设计，但其代数结构复杂，根据模运算设计电路难度较大[8]。为充分发挥电流信号的运算特点，本文提出了阈算术代数系统，定义阈算术运算及非负运算为其基本运算，提出以阈算术函数表示电流型电路的逻辑关系，并定义了阈算术函数的图形表示——和图。进一步提出基于和图的三值电流型CMOS电路设计方法，所设计的电路结构简单，经HSPICE仿真软件模拟具有正确的逻辑功能。和图在电流型CMOS电路设计中的应用，达到了简化电流型电路设计的目的。

2 阈算术代数系统

首先提出一个对任意基数R完备的运算集合，其中定义信号变量x,y,z∈ ( 0,1,2,… ,m)为m值逻辑信号，阈值t,t1,t2∈(0.5,1.5,… ,m-0.5),m为正整数。下面定义基本运算。

定义1阈算术运算。

文献[11]建立了基于开关-信号理论的电流型电路设计方法。将电路中的变量分为状态变量与信号变量，并提出了它们相互作用的联结运算。

联结运算I：描写开关信号控制元件开关状态的物理过程。

联结运算II：描写开关状态控制信号操作的物理过程。

开关：信号理论就是通过信号与阈值的比较控制开关的通断从而实现对信号传输的控制。为建立阈算术代数系统，本文将两个联结运算结合，提出阈算术运算，其定义为

(1)高阈算术运算：

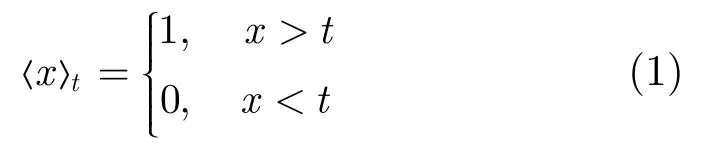
(2)低阈算术运算：

(3)双阈算术运算：

式(1)-式(3)中，x∈ ( 0,1,2,… ,m)，阈值t,t1,t2∈(0.5,1.5,…,m-0.5),m为正整数。

电流型CMOS电路中，包括串联开关传输运算与并联开关传输运算。串联开关传输运算可由阈算术运算及乘法运算直接实现。对于并联开关传输运算，其物理意义为当电路中有一个开关导通，就能实现信号的传输，为此本文定义了并阈算术运算，以符号“∨”表示，如式(4)所示。

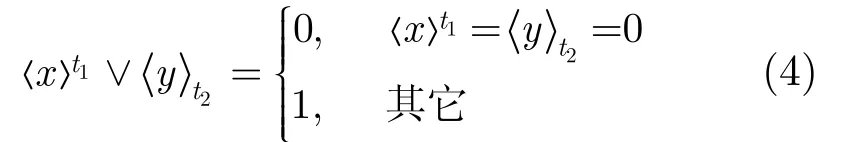
我们规定并阈算术运算“∨”的优先级高于乘法运算“·”。

根据阈算术运算的特点，可有如下性质：

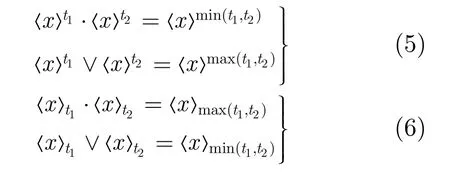
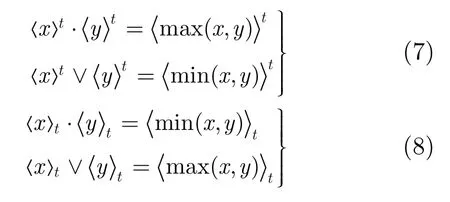
定义2非负运算。

普通算术运算中包含减法运算，由其构成的函数运算结果可为正值或负值，正负值混合情况的出现使代数运算复杂化。并且应用于电流型电路，正值及负值分别代表电流信号的正向及反向，电流的双向性使电路结构复杂化。为避免此种情况，需限制函数值的取值范围，因此本文定义了非负运算：

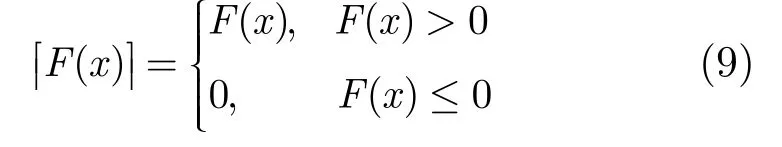
式(9)中变量x∈ ( 0,1,2,… ,m),F(x)表示由算术运算和阈算术运算组成的函数。

定义3阈算术代数系统与阈算术函数。

以算术运算、非负运算及阈算术运算为基本运算组成的代数系统称为阈算术代数系统，其逻辑关系的解析表示称为阈算术函数。

要建立一个代数系统，首先必须证明其基本运算构成完备运算集。根据文献[8]，如果使用某组运算集合可以把任何单变量函数以变量与诸函数值之间的具体运算给予表示，那该组运算集合也可用于表示更多变量的函数，并因此而组成完备运算集。

由阈算术运算的特点，可以方便地得到任意三值单变量阈算术函数F(x)的如下表示：

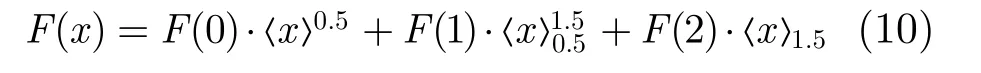
为便于区分，本文规定以大写F表示的函数为阈算术函数，以小写f表示的函数为逻辑函数，在逻辑函数中“.”“+”分别表示“与”“或”运算，而在阈算术函数中“.”“+”则分别表示算术乘法运算和算术加法运算，表示乘法的点符可省略。按照文献[8]的定理即可证明阈算术运算和算术运算组成完备运算集。

由式(10)通过对变量的逐次展开可获得有更多变量的函数的规范展开，以二变量三值阈算术函数F(x,y)为例，可有

仿照二值代数中的术语，式(11)各项中阈算术运算的乘积可称为最小项，各变量取值下的阈算术函数值为最小项对应的系数。

可以证明在三值代数系统中有如下性质：

(a)相补率：

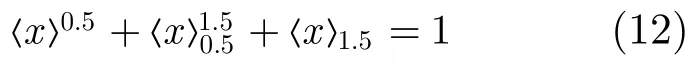
(b)变量还原律：

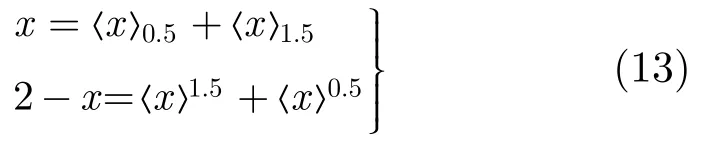
(c)阈值变换律：

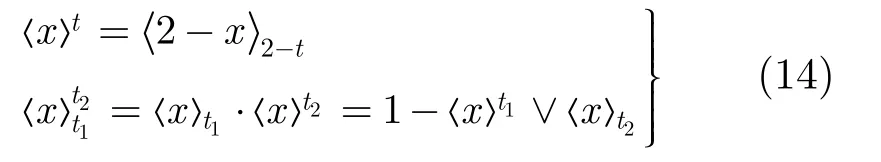
式(13)，式(14)中，2 -x即为三值逻辑代数中变量x的非运算。

定义4和图。阈算术函数的图形表示，称为和图。

与逻辑函数的K图相似，本文提出和图为阈算术函数的图形表示。和图坐标排列与K图一样，其中格内填入值为对应变量取值下的阈算术函数值。如图1为一个任意二变量三值阈算术函数F(x,y)的和图。

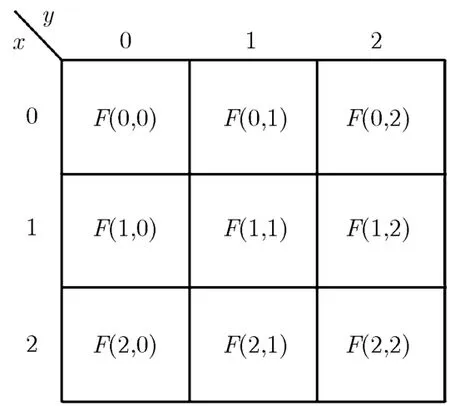
图1 和图的一般表示

从和图的定义可知，K图实际上也是和图，是和图的一个子集。通过和图表示阈算术函数使其特点清晰，各输入输出项之间的关系可以得到直观判定，并且阈算术函数间的相互运算可通过对应的和图经阈算术代数运算直接得到，和图的这一特性对于阈算术函数的简化具有重要的作用。

3 基于和图的三值电流型CMOS电路设计

电路的结构设计取决于其所对应函数的运算关系。本文阈算术代数系统理论根据电流型电路易于实现算术运算的特点提出，充分发挥了电流信号在算术运算中的潜力，阈算术函数由算术运算、非负运算、阈算术运算为基本运算组成，相较于传统逻辑函数的表示方式具有显著优势。

逻辑电路基本的电路单元是构成电路的基础，电流型CMOS电路中加、减、倍乘等算术运算对应的电路单元可通过电流镜及线接方便地实现[12]，图2为本文提出的电流型 CMOS电路阈算术运算实现。根据逻辑电路的阈算术函数表示，结合电流型CMOS电路的基本算术单元，可以方便地设计出对应的电流型电路。

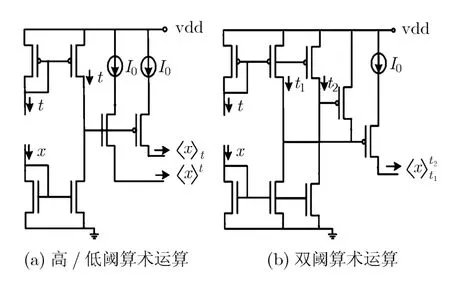
图2 电流型CMOS阈算术运算电路

本文以三值电流型CMOS电路设计为例，提出一种基于和图的三值电流型CMOS电路设计方法。K图是和图的一个子集，我们将待设计逻辑函数的K图称为目标和图，可以写出阈算术函数规范展开形式，再通过式(12)-式(14)的性质化简函数式。结合图2所示的单元电路就可以设计出相应的电流型CMOS电路。然而阈算术函数的函数式往往较为复杂，难以直观采用阈算术运算的性质化简。为此本文提出一种基于和图设计三值电流型 CMOS电路的方法，步骤如下：

(1)根据所需设计电路的逻辑函数，画出K图，即目标和图。

(2)观察目标和图的特点，构造一个较为简单的阈算术函数，使其和图与目标和图尽可能相似。

(3)再构造一个或多个和图将其与步骤(2)的和图进行阈算术代数运算得到目标和图，由此图形运算过程求得对应的阈算术函数表达式。

(4)根据所得的阈算术函数，结合图2的单元电路，设计出相应的三值电流型CMOS电路。

步骤(3)中，和图的阈算术代数运算具体包括阈算术运算及加法、减法(非负)、乘法 3种算术运算形式。图3所示为高阈算术运算相应的和图运算。

例1设计三值比较运算的电流型 CMOS电路。当x＞y时，输出为0;x=y时，输出为1;x＜y时，输出为2。

如图4(a)为三值比较运算的K图，即目标和图。由比较运算包含的实际算术意义，容易想到对x与y做相减运算，结合目标和图的特点，可构造出阈算术函数F1(x,y) =y+ 1-x，其和图与目标和图相似，如图4(b)所示。

图3 和图的高阈算术代数运算

比较图 4(a), 4(b)，对所构造的阈算术函数F1(x,y)做进一步的阈算术代数运算，使最终得到的阈算术函数的和图与目标和图相同，由此可得

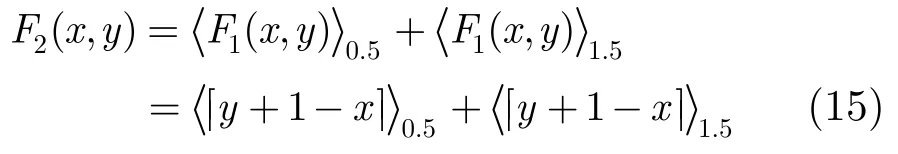
根据式(15)设计出三值比较运算的电流型CMOS电路，如图4(c)所示，输入电流信号x首先经过电流镜反向再接入电路。

例2设计三值二变量模三乘运算f1(x,y)=x⊗y的电流型CMOS电路。

模三乘运算的目标和图如图 5(a)所示，由目标和图发现在x=0或y=0时，阈算术函数的值为0。因此f1(x,y)对应的阈算术函数可以表示成如下形式：

图4 三值比较运算的电流型CMOS电路

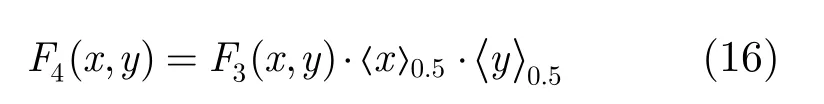
式(16)中函数F3(x,y)表示对目标和图进行裁剪，即不考虑x=0或y=0的和图对应的阈算术函数。裁剪后变量x与y的取值范围由三值变为二值，目标和图的规模大幅减少。构造和图并通过图形间的相互运算得到最终和图，过程如图5(b)所示。

由图5(b)得出阈算术函数F3(x,y)的表达式：

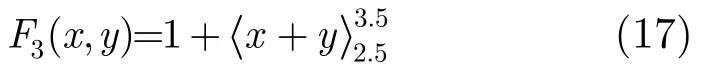
因此，模三乘运算经和图化简后，最终的阈算术函数表达式为

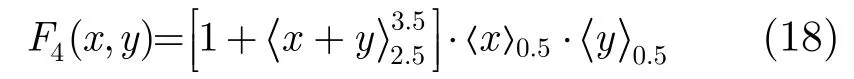
由式(18)设计出二变量模三乘运算的电流型CMOS电路，如图5(c)所示。

采用TSMC 0.18 μm CMOS标准工艺参数对图5(c)电路进行Hspice模拟，模拟时选取逻辑值(0, 1,2)相对应的电流值分别为(0, 10 μA, 20 μA)，并取vdd=1.8 V，负载为图2(a)所示高阈算术运算电路。模拟得到的电路瞬态特性如图5(d)所示，模拟结果表明所设计电路具有正确的逻辑功能，电路的平均延迟为0.69 ns，体现了电流型电路的高速特点。

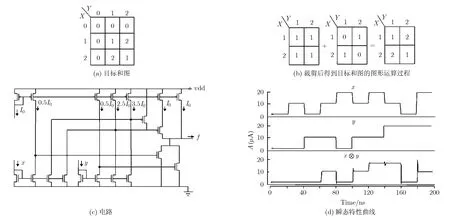
图5 二变量模三乘运算的电流型CMOS电路

例2二变量模三乘运算的电流型CMOS电路设计过程，充分发挥了图形表示的直观性，利用目标和图构造阈算术函数，再通过所构造的阈算术函数的和图与目标和图比较，对阈算术函数做进一步阈算术代数处理，最终得出所设计逻辑函数的阈算术函数表示。和图方法的设计过程具有规范性和普遍适用性。电路设计的过程简单，所设计的电路结构简单并且具有整形功能。阈代数系统及和图方法的运用简化了电流型CMOS电路的设计。目前电流型数字电路设计的主要方法是由开关-信号理论作指导[6,8,12,13]，但开关-信号理论中电流型电路定义的基本运算未充分运用电流信号易于求和、相减、倍乘等特性。并且开关-信号理论指导电流型电路设计时，没有提出系统的逻辑函数化简方法，逻辑电路的函数表示往往通过其真值表或K图直接得到，电路设计过程具有特殊性。本文提出的阈算术代数系统理论及基于和图的设计方法，充分利用电流信号易于求和、相减、倍乘的特性，使电流型电路的设计及函数化简过程简单、规范。因此本文提出的阈算术代数系统及电流型电路设计方法具有系统、规范和高效的特点。

4 结束语

电流信号易于实现算术运算，这一特性使电流型电路在算术运算和多值领域展示了巨大潜力。本文定义了阈算术运算、非负运算，证明了阈算术运算与算术运算构成完备集，从而建立了阈算术代数系统，并进一步提出了和图为阈算术函数的图形表示。最后将阈算术代数系统应用于三值电流型CMOS电路设计，提出了基于和图的电流型三值CMOS电路设计方法，利用和图将逻辑函数表示成阈算术函数形式，所得的函数形式简单，适合电流型CMOS电路的实现。所设计的电路经Hspice模拟具有正确的逻辑功能，阈算术代数系统的提出为电流型电路的设计提供了一种新的简单有效的方法。

[1]Aan-Tuan D, Kong Z H, Yeo K S,et al.. Design and sensitivity analysis of a new current-mode sense amplifier for low-power SRAM[J].IEEE Transactions on Very Large Scale Integration(VLSI)Systems, 2011, 19(2): 196-204.

[2]殷树娟, 李翔宇, 孙义和. 标准数字工艺下 16位精度低电压低功耗∑△模数调制器设计[J]. 电子与信息学报, 2010, 32(1):464-469.

Yin Shu-juan, Li Xiang-yu, and Sun Yi-he. Design of 16 bit low-power ∑△ modulator with standard digital technology[J].Journal of Electronics&Information Technolgy, 2010,32(1): 464-469.

[3]Trescases O, ProdiA, and Wai Tung-ng. Digitally controlled current-mode DC-DC converter IC[J].IEEE Transactions on Circuits and Systems,2011, 58(1): 219-231.

[4]Yuan F. Low-voltage CMOS current-mode circuits: topology and characteristics[J].IEE Proceedings-Circuits Devices and Systems, 2006, 153(3): 219-230.

[5]Bhatia V, Pandey N, and Bhattacharyya A. A 4-bit expandable algorithmic current-mode analog to digital converter for use in digital control systems[C]. India International Conference on Power Electronics (IICPE),New Delhi: IICPE, 2010: 1-4.

[6]盛法生, 杭国强, 吴训威. 多值模运算的 I2L电路实现[J]. 浙江大学学报(理学版), 2002, 29(1): 50-54.

Sheng Fa-sheng, Hang Guo-qiang, and Wu Xun-wei. I2L circuits design of multiple-valued modulo-operations [J].Journal of Zhejiang University(Science Edition), 2002, 29(1):50-54.

[7]高虹, 汪鹏君. 三值钟控传输门绝热逻辑电路研究[J]. 电路与系统学报, 2011, 16(3): 93-97.

Gao Hong and Wang Peng-jun. Study on ternary clocked transimission gate adiabatic logic circuit[J].Journal of Circuits and Systems, 2011, 16(3): 93-97.

[8]吴训威. 多值逻辑电路设计原理[M]. 杭州: 杭州大学出版社,1994: 18-46.

Wu Xun-wei. Design Principles of Multivalued Logic Circuits[M]. Hangzhou: Hangzhou University Press, 1994: 18-46.

[9]杭国强, 应时彦. 新型电流型CMOS四值边沿触发器设计[J].浙江大学学报(工学版), 2009, 43(8): 1970-1974.

Hang Guo-qiang and Ying Shi-yan. Novel current-mode CMOS qunaternary edge-triggered flip-flops [J].Journal of Zhejiang University(Engineering Science), 2009, 43(8):1970-1974.

[10]El-Hariry Yassmeen M, and Madian A H. MOS Current mode logic realization of digital arithmetic circuits[C]. 2010 International Conference on Microelectronics (ICM 2010),Cario: ICM, 2010: 128-131.

[11]Wu X W and Deng X W. Design of ternary current-mode CMOS circuits based on switch-signal theory[J].Journal of Electronics, 1993, 10(3): 193-202.

[12]沈继忠, 邵志龙, 蒋征科. 基于并联开关的低电压低功耗电流型 CMOS电路设计[J]. 电子与信息学报, 2004, 26(8):1325-1331.

Shen Ji-zhong and Shao Zhi-long, Jiang Zheng-ke. Design of low voltage low power current-mode CMOS circuits based on parallel switches[J].Journal of Electronics&Information Technolgy, 2004, 26(8): 1325-1331.

[13]杭国强. 基于开关信号理论的电流型CMOS多值施密特电路设计[J]. 电子学报, 2006, 34(5): 924-927.

Hang Guo-qiang. Design of current-mode CMOS multiplevalued Schmitt triggers based on switch-signal theory[J].Acta Electronica Sinica, 2006, 34(5): 924-927.