非耗散耦合复杂网络受控同步能力分析
刘歌群 许晓鸣
(上海理工大学光电信息与计算机工程学院 上海 200093)
1 引言
复杂网络[1,2]因刻画了复杂系统的本质特征而成为研究热点,同步[3,4]作为复杂网络重要的动力学行为而备受关注。目前多数研究工作采用了耗散耦合网络模型[3-11],耗散耦合是网络节点通过状态变量之差耦合的一种情况[5],当节点通过状态变量直接耦合时,网络就不再是耗散耦合的,如产品价格网络,甲产品的价格直接进入乙产品的成本,又如交通网络,A路口的车辆直接行驶进入B路口。鉴于非耗散耦合网络巨大的应用意义[6-10],其同步问题需要研究。
网络在两种情况下可能取得同步,一是自同步,二是通过控制同步,因此网络有两种同步能力,即自同步能力和受控同步能力。文献[11]提出了研究复杂网络同步问题的主稳定函数法[11,12],对于耗散耦合网络,文献[13,14]发现,当同步化区域为 (- ∞,a1)形无限区间时,外耦合矩阵第二大特征值越小网络同步能力越强,文献[15]指出,当同步化区域为有限区间时,外耦合矩阵最小特征值与第二大特征值之比越小,网络同步能力越强。这些结论指的都是耗散耦合网络的自同步能力[16],而对于非耗散耦合网络,因为网络不可能自同步,所以只能分析它的受控同步[6,7,17]能力。与耗散耦合网络的自同步能力相对应,非耗散耦合网络的耦合强度及外耦合矩阵特征值对网络受控同步能力会有什么影响,目前很少看到相关结果,为此本文对这一问题进行专门研究。
2 非耗散耦合网络模型及预备知识
考虑如下的线性时不变非耗散耦合复杂动态网络:
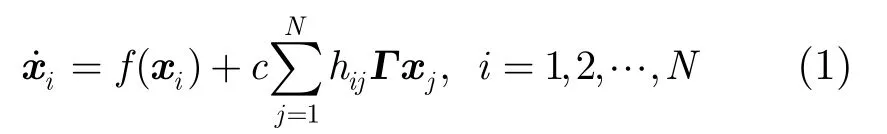
当外耦合矩阵对角线元素非零且满足矩阵行和为0时,网络为耗散耦合网络。耗散耦合网络外耦合矩阵有且仅有一个重数为1的0特征根,对应的右特征向量为 (1 /) [1,1,… , 1 ]T, 0为最大特征值,对应同步流形[3,11,16]。非耗散耦合网络与耗散耦合网络在结构上的主要区别在于外耦合矩阵主对角线元素,为了对非耗散耦合网络的受控同步能力进行分析,先给出非耗散耦合网络外耦合矩阵特征值的分布规律。设lmin=lN≤…≤l2≤l1=lmax为H的N个特征值,由矩阵理论,有以下结论。
引理1

利用矩阵理论可以很容易得到本引理。引理 1表明,非耗散耦合网络外耦合矩阵的特征值有正有负,分布在原点两侧。
在动态网络式(1)中,当t→∞时若x1(t)→x2(t)→ … →xN(t) →s(t),则称网络达到渐近同步。同步状态s(t) ∈Rn为孤立节点状态方程的解,可以是平衡点、混沌轨道或者周期轨道,满足˙(t)=f(s(t))。
3 非耗散耦合网络同步控制律与受控同步能力分析
把网络式(1)在同步状态s(t)上线性化,令yi(t) =xi(t) -s(t),得到方程

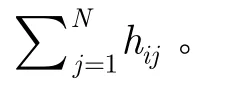
注释1式(3)中由于项ckiΓs(t)的存在,若s(t)≠ 0 且节点i不施加控制,则在yi(t) → 0时˙i(t)→ckiΓs(t) ≠ 0 ,网络同步状态不稳定,所以非耗散耦合网络不能自同步。这一点是非耗散耦合网络与耗散耦合网络在同步能力上的根本区别,耗散耦合网络满足特定条件[3,4,11-16]时可以自同步,而非耗散耦合网络不存在自同步的可能性,只能通过分散控制[6,7]实现同步。
考虑控制律

把控制律式(4)施加于网络式(1)得到闭环网络

注释2控制律式(4)是一种对消控制,即通过项 -ckiΓs(t)把使得网络同步状态不稳定的因素对消掉。对消控制是控制工程及复杂网络控制中常见的一种手段[18-20],因为参数ki已知,所以控制律式(4)是易行的。由于非耗散耦合网络在现实世界中普遍存在,其同步问题异常重要[1,2,6-10,21],对同步不稳定项进行处理是非耗散耦合网络同步研究绕不开的问题,控制律式(4)给出了一种可行方法。
注释3引入 -ckiΓs(t)的网络与耗散耦合网络并不相同。耗散耦合网络通过状态变量之差进行耦合的方式,相当于每个节点自动引入 -ckiΓxi(t),而控制律式(4)给每个节点引入的是 -ckiΓs(t),所以网络式(5)与常见的受控耗散耦合网络[1,3,4,7,14]并不相同,因此本文考虑的是新问题。
注释4复杂网络受控同步能力因控制方式而异,控制律不同,网络参数对受控同步能力的影响也不同。控制律式(4)采用了内耦合矩阵形式的反馈控制,所以本文分析的网络受控同步能力是“内耦合形反馈控制意义下的”受控同步能力。之所以选择内耦合形反馈控制,原因有二:一是该反馈形式与网络节点之间的耦合方式相同,反馈阵为cd倍的Γ,与网络本身结构特征一致,易于实现且待设计参数只有一个,即d;二是该反馈形式非常流行,为已有大多数文献所采用,如文献[1,3,4,11,12,14]。

令D=dIN,特征矩阵G为利用Kronecker积把闭环网络式(5)整理为紧凑形式

易知特征矩阵G为实对称阵,故存在非奇异阵P∈RN×N使P-1GP=Λ, 其 中Λ=diag(m1,m2,…,mN),mN≤…≤m2≤m1为G的特征值。利用相似变换y(t) = (P⊗In)η(t),把网络式(7)变换为N个解耦的低维子系统

由文献[11,16],使得网络式(8)主稳定方程系统阵为
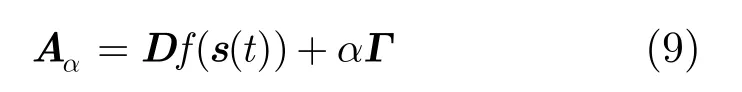

定理1当∃Si⊆S使c(l1-lN) <ai2-ai1时,网络式(1)可在控制律式(4)作用下在s(t)取得同步,控制增益d∈ (ai1/c-lN,ai2/c-l1)。
证明由同步化区域定义及文献[3,11,13-16],当cmi∈Si,i= 1 ,2,… ,N时受控网络式(5)在s(t)取得同步。因G=H+dIN,有mi=li+d,i=1,2,…,N,同步条件变为cli+cd∈Si,i= 1,2,… ,N。再由H阵的特征值为实数,lN和l1分别为最小与最大特征值,可知c(l1-lN)为G阵特征值在实轴上分布范围的宽度,通过选择cd可使该范围在实轴上平移。故当c(l1-lN) <ai2-ai1时,可通过选d∈(ai1/c-lN,ai2/c-l1)使条件cli+cd∈Si,i=1,2,…,N满足,从而使受控网络式(5)在s(t)取得同步。证毕
注释5定理1表明,l1-lN越小,非耗散耦合网络越容易通过控制取得同步,网络同步能力也就越强。

以下考虑孤立同步化区域包含原点的情况,即0∈Si的情况。
定理2若 ∃Si= (ai1,ai2)⊆S,其中ai1<0,ai2> 0 ,选控制增益d=0,则非耗散耦合网络式(1)在控制律式(4)作用下在s(t)取得同步的条件为c<min(ai1/lN,ai2/l1)。
证明当c<min(ai1/lN,ai2/l1),d=0时,总有(clN+cd,cl1+cd) = (clN,cl1)⊆ (ai1,ai2),由同步化区域定义及文献[3,11,13-16],受控网络式(5)在s(t)取得同步。 证毕
注释7定理 2表明,当孤立同步化区域包含原点时,非耗散耦合网络可以通过耦合强度的缩放实现同步,此时控制律式(4)退化为

控制律式(10)施加于网络之后,受控网络从形式上看相当于耗散耦合网络,但由注释3分析可知,它并不是耗散耦合网络。另外这种情况下网络参数对同步能力的影响与耗散耦合网络也是不同的。
以下再考虑定理1中Si为无限区间的情况。
推论1若 ∃Si=(- ∞,ai2)⊆S, - ∞ <ai2<∞,则网络式(1)总可在控制律式(4)作用下在s(t)取得同步,控制增益d∈(- ∞,ai2/c-l1)。
证明显然ai1=-∞,因c,l1,lN为有限值,总有c(l1-lN) <ai2-ai1=ai2-(- ∞) =∞ 成立使定理1条件满足,由定理1可知推论1结论成立,控 制 增 益d∈ (ai1/c-lN,ai2/c-l1) = (- ∞,ai2/c-l1)。 证毕
注释8推论1表明,当网络包含 (- ∞,a2)型孤立同步化区域时,其中 - ∞<a2<∞,非耗散耦合网络总能通过控制取得同步,控制增益最小幅值取决于耦合强度及外耦合矩阵最大特征值。
推论2若 ∃Si= (ai1,∞ )⊆S,- ∞ <ai1< ∞ ,则网络式(1)总可在控制律式(4)作用下在s(t)取得同步,控制增益d∈ (ai1/c-lN, ∞ )。
证明因ai2=∞,与推论 1证明过程类似,可知推论2成立。 证毕
注释9推论 2表明,当网络包含(a1,∞)型孤立同步化区域时,其中 - ∞<a1<∞,非耗散耦合网络总能通过控制取得同步,控制增益最小幅值取决于耦合强度及外耦合矩阵最小特征值。
4 仿真分析
已知Lorenz系统[23]节点动力学方程为

该系统的混沌轨道见图 1。 利用 Lorenz系统构成20节点非耗散耦合小世界网络[24]见图2。


图1 Lorenz振子 x i 1 -x i 3相轨迹曲线图
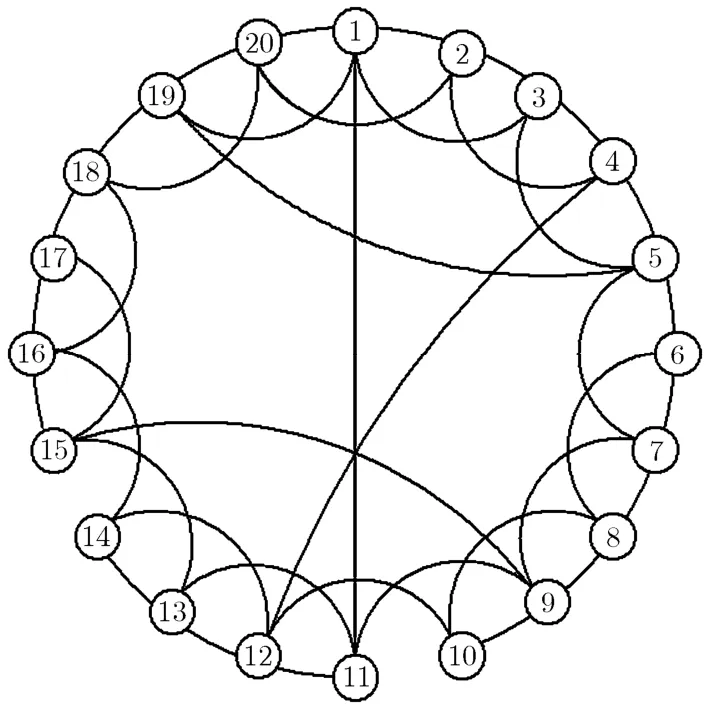
图2 网络拓扑结构
设内耦合矩阵为已知同步化区域S=(-5 2,- 2 4),外耦合矩阵特征值lN=- 2 .8602,l1= 4 .1096。
选c=0.1,d=- 5 00时网络同步曲线如图3所示,选c=1,d=- 3 8时网络同步曲线如图4所示,选c=4,d=-1 0.13时网络同步曲线如图5所示,选c=10,d=-4时网络同步曲线如图6所示。
由同步化区域范围可知,本例中0∉S。根据定理1,耦合强度c=0.1时控制增益范围为(-517.198,-244.1096),耦合强度c=1时控制增益范围为(- 4 9.1398,- 2 8.1096),耦合强度c=4时控制增益范围为(- 1 0.1398,- 1 0.1096),耦合强度c=10时控制增益范围为∅。图3~图5中,控制增益选在范围之内,网络都取得了同步,而图6由于c=10时定理1条件不能满足,网络不能同步。从所计算的控制增益范围可以看出,当耦合强度较小即c=0.1时,控制增益的绝对值比较大,为350左右,而随着耦合强度从c=0.1增大到c=1再增大到c=4,控制增益的绝对值也从 350左右减小到 35左右再减小到10左右,由此说明随着耦合强度的增大,网络实现同步控制所需要的控制增益绝对值越来越小。在c= 4 时,控制增益范围比较小,这种情况下受控网络同步过程较慢(见图5)。
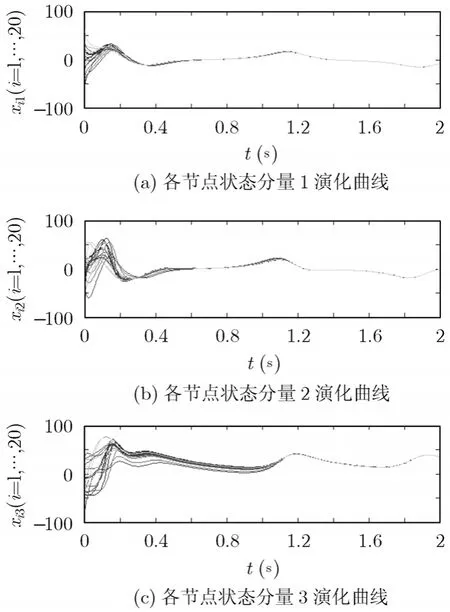
图3 网络同步曲线(c=0.1,d =-5 00)
5 结论

图4 网络同步曲线(c=1,d =-3 8)

图5 网络同步曲线(c=4,d =-1 0.13)

图6 网络同步曲线(c=10,d=-4)
非耗散耦合网络在现实中普遍存在,但其同步问题的报道并不多见。从本文分析可知,非耗散耦合网络不能自同步,其同步能力要从受控同步的角度进行分析,这一点恰是非耗散耦合网络同步问题的特殊性。本文研究了非耗散耦合网络“在内耦合形反馈控制意义下的”同步能力。研究发现,非耗散耦合网络的受控同步能力与耗散耦合网络的自同步能力不同,耦合强度越小,网络通过控制取得同步的可能性越大,但在同步化区域不包含原点的情况下所需要的控制增益绝对值也越大。此外,外耦合矩阵最大最小特征值之差越小,网络受控同步能力越强,这一点与I型及II型耗散耦合网络[13-16]的自同步能力规律也是不同的。非耗散耦合网络与耗散耦合网络同步能力上的差异源于外耦合矩阵特征值的分布规律,正如引理1所述,非耗散耦合网络外耦合矩阵的特征值分布在原点两侧,不象耗散耦合网络那样分布在原点及负实轴上,所以网络同步能力对外耦合矩阵最大最小特征值及耦合强度的依赖性不同。本文研究结论对于非耗散耦合网络的构建具有参考意义,该结论指明,如何选择网络参数可使网络所需同步控制增益幅值更小、能耗更低,可使网络更容易通过控制取得同步。
[1]郭雷, 许晓鸣(主编). 复杂网络[M]. 上海: 上海科技教育出版社, 2006: 1-20.
Guo Lei and Xu Xiao-ming. Complex Networks[M]. Shanghai:Shanghai Scientific & Technological Education Publishing House, 2006: 1-20.
[2]Dorogovtsev S N. Lectures on Complex Networks[M]. Oxford:Clarendon Press, 2010: 1-15.
[3]Chen Guan-rong, Wang Xiao-fan, Li Xiang,et al.. Some Recent Advances in Complex Networks Synchronization. In:Kyamakya K. Recent Advances in Nonlinear Dynamics and Synchronization[M]. Springer-Verlag Berlin Heidelberg, 2009:3-16.
[4]Delellis P, Bernardo M, Gorochowski E,et al..Synchronazation and control of complex networks via contraction, adaption and evolution[J].IEEE Circuits and Systems Magazine, 2010, 10(3): 64-82.
[5]Sepulchre J A and Babloyantz A. Controlling chaos in a network of oscillators[J].Physical Review E, 1993, 48(2):945-950.
[6]Siljak D D and Zecevic A I. Control of large-scale systems:beyond decentralized feedback[J].Annual Reviews in Control,2005, 29(2): 169-179.
[7]Duan Zhi-sheng, Wang Jin-zhi, Chen Guan-rong,et al..Stability analysis and decentralized control of a class of complex dynamical networks[J].Automatica, 2008, 44(4):1028-1035.
[8]Liu Hui, Lu Jun-an, Lv Jin-hu,et al.. Structure identification of uncertain general complex dynamical networks with time delay[J].Automatica, 2009, 45(8): 1799-1807.
[9]Yao Jing, Guan Zhi-hong, and Hill D J. Passivity-based control and synchronization of general complex dynamical networks[J].Automatica, 2009, 45(9): 2107-2113.
[10]Xu Yu-hua, Zhou Wu-neng, Fang Jian-an,et al.. Structure identification and adaptive synchronization of uncertain general complex dynamical networks[J].Physics Letters A,2009, 374(2): 272-278.
[11]Pecora L M and Carroll T L. Master stability functions for synchronization coulped systems[J].Physical Review Letters,1998, 80(10): 2109-2112.
[12]Sorrentino F and Porfiri M. Analysis of parameter mismatches in the master stability function for network synchronization[J].Europhysics Letters, 2011, 93(5): 50002.
[13]Wang X F and Chen G. Synchronization in scale-free dynamical networks: robustness and fragility[J].IEEE Transactions on Circuits&SystemsI, 2002, 49(1): 54-62.
[14]Wang Xiao-fan and Chen Guan-rong. Pinning control of scale-free dynamical networks[J].Physica A, 2002, 310(3,4):521-531.
[15]Barahona M and Pecora L M. Synchronization in Small-World Systems[J].Physical Review Letters, 2002, 89(5):054101.
[16]Chen Yong-hong, Rangarajan G, and Ding Ming-zhou.General stability analysis of synchronized dynamics in coupled systems[J].Physical Review E, 2003, 67(2): 026209.
[17]Liu Yang-yu, Slotine J J, and Barabasi A L. Controllability of complex networks[J].Nature, 2011, 473(7346): 167-173.
[18]Fan Chun-xia, Jiang Guo-ping, and Jiang Feng-hua.Synchronization between two complex dynamical networks using scalar signals under pinning control[J].IEEE Transactions on Circuits And SystemsI, 2010, 57(11):2991-2998.
[19]Hu Cheng, Yu Juan, Jiang Hai-jun,et al.. Synchronization of complex community networks with nonidentical nodes and adaptive coupling strength[J].Physics Letters A, 2011, 375(5):873-879.
[20]Wu Jian-she, Jiao Li-cheng, and Chen Guan-rong. Cluster synchronization in a network of non-identical dynamic systems[J].Chinese Physics B, 2011, 20(6): 060503.
[21]龚美静, 瞿少成, 王晓燕. 一种通过异结构同步实现混沌保密通信新方法[J]. 电子与信息学报, 2009, 31(6): 1442-1444.
Gong Mei-jing, Qu Shao-cheng, and Wang Xiao-yan. A novel method of realizing chaotic secure communication by synchronization of different structure[J].Journal of Electronics&Information Technology, 2009, 31(6):1442-1444.
[22]Duan Zhi-sheng, Chen Guan-rong, and Huang Lin.Disconnected synchronization regions of complex dynamical networks[J].IEEE Transactions on Automatic Control, 2009,54(4): 845-849.
[23]Lorenz E N. Deterministic nonperiodic flow[J].Journal of the Atmospheric Siences, 1963, 20: 130-141.
[24]Watts D J and Strogatz S H. Collective dynamics of small-world networks[J].Nature, 1998, 393(6684): 440-442.

