大气噪声模型参数的非线性回归估计
1 引言
在超低频通信系统中,大气噪声的干扰一直困扰着通信工作者。大气噪声是由雷电等噪声源引起,是一种典型的非高斯噪声[1-3]。然而目前通信系统的最优接收机都是在高斯噪声背景假设的前提下设计的,在实际中往往达不到预期的性能,甚至有时会导致接收机性能的恶化。随着电子技术的蓬勃发展以及对通信质量的需求的不断提升,对于大气噪声的研究越来越引起超低频工作者的兴趣[4,5]。大气噪声的研究,早在上个世纪50年代就已开展,但那时主要的工作集中于对大气噪声模型的建立。模型流派主要有两类,一类是经验模型,另一类是分析模型。其中分析模型虽然比经验模型表达式更复杂,但因为有实际的物理过程支撑,且同实测数据也有更好的一致性,因此得到了长足的发展。分析模型中最著名也应用最广的是Middleton的统计物理模型,该模型通过对噪声源泊松分布的假设,详细分析了噪声传播过程,推导了噪声的概率模型[6,7]。该模型主要可分为Class A 噪声模型和Class B噪声模型。Class A 噪声带宽小于接收机带宽,一般应用于宽带系统;Class B噪声带宽大于接收机带宽,较多应用于窄带系统。由于在实际中,超低频接收机一般设计为窄带接收机,因此本文研究的大气噪声模型为Class B噪声模型。
自Class B模型的诞生之后,由于其概率密度函数表达式复杂,信号处理难度较大,因此有些学者将α稳定过程作为Class B模型的一种简化形式,以此来研究非高斯噪声[8,9]。然而,在实际中,接收机不仅受到非高斯噪声的影响,而且同时会受到高斯噪声影响。这部分高斯噪声不仅会来自于接收机系统内部,也会来自于外部。因此,在实践中,α稳定过程作为大气噪声模型在性能比Class B模型要差[7]。然而,由于Class B模型的复杂,对Class B噪声的研究甚少,特别在Class B参数估计上,只有Middleton的一些成果。而且这些成果一般都基于经验分析,在实际中性能不理想,特别是难以应用于实时信号处理中,特别是接收机的设计中。本文从特征函数出发,采用非线性回归估计,并设计了初始值估计方案和特殊序列,快速估计了Class B噪声模型参数。实验表明,该方法精度高,迭代收敛快,有很高的实用价值。
2 Class B模型
Middleton通过对噪声产生和传播机制的建模,推导出Class B噪声模型。Middleton假设噪声由高斯背景噪声N(t)和脉冲噪声X(t)构成。X(t)由一系列接收到的干涉波形组成。
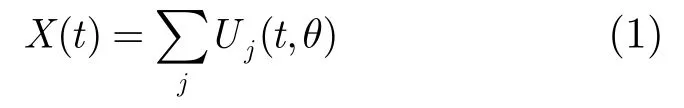
其中Uj(t,θ)代表第j个干扰源产生的波形,θ代表相关的各种参数。假设在时间和空间上波形产生服从泊松分布,最终可推得概率密度函数[7]
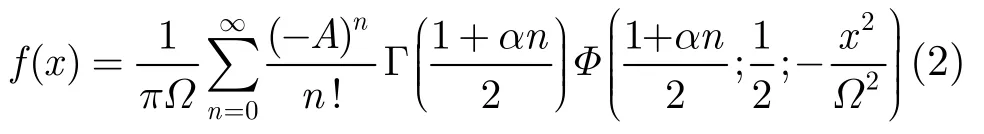
其中A是“重叠系数”(overlap index),也称为“脉冲系数”(impulsive index),指干扰源在单位时间平均发射的数目。α是空间传输密度因子,一般取0<α<2。Ω为归一化因子。Γ(x)代表Γ函数,而Φ(a;b;x)指的是合流超几何分布。从式(2)可以看出Class B噪声模型的概率密度表达式是级数形式,表达式复杂,且是正负项交替,收敛速度慢。也正因为这,使得对Class B噪声模型参数估计造成了很大难度。虽然其概率密度表达式复杂,但特征函数却相对简单,且是闭合形式[7]。
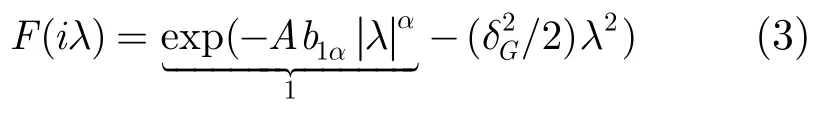
其中b1α是α的函数,是高斯噪声分量。如果单独取式(3)中的第1项作为近似,则Class B噪声模型就退化成对称α稳定分布(Sα S)。其实高斯分布本质上也是Sα S分布的特例,即α=2。从另一个方面说,Class B模型可以看成对称α稳定过程(Sα S)和独立高斯过程(G)的混和模型。下一节将从式(3)出发,推导非线性回归模型。
3 非线性回归估计
不妨将式(3)中,用γ替换Ab1α,指代Sα S过程中的离差(dispersion),于是式(3)等价于
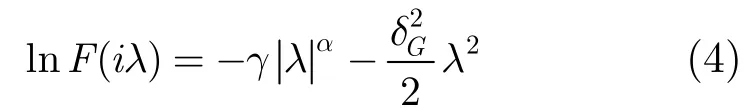
根据特征函数的定义有

若设观测到的数据为{xk},k= 1 ,… ,N,则式(5)的估计为
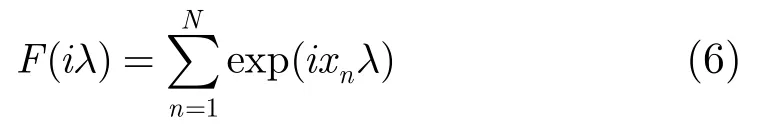
结合式(4)和式(6)有
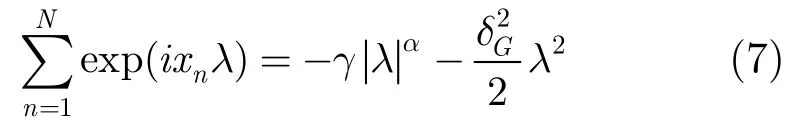
因此通过特定的序列{λk},可以利用非线性回归方法求解式(7)。
设θ= {α,γ,δG} = {θ1,θ2,θ3}为F(iλ)的参数空间。将F(iλi,θ)在θ0展开有
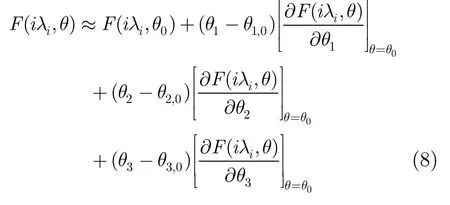
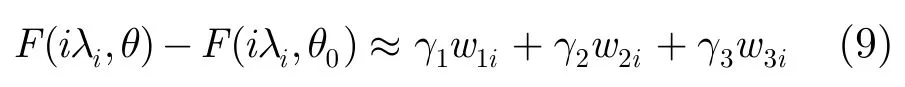
对于式(9),可以通过线性回归方法求解,即
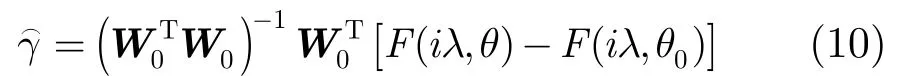
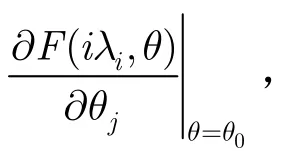
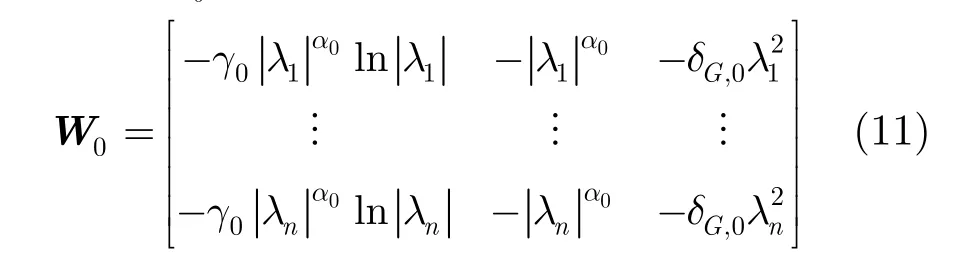
设平方误差为
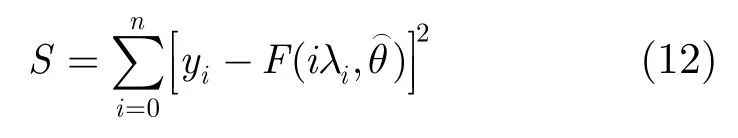
因此,为了使在迭代过程中满足式(12)不断收敛,优化后的非线性回归算法为:
步骤1 估计初始参数θ0;
4 初始值估计和{λk}序列的生成
由于对估计Class B的参数的文献较少,没有已知的较好的经验估计方案,因此本文提出一种新的思路粗略估计Class B参数作为初始值。可以看到,Class B噪声模型本质上是两个α稳定过程的混和模型,其中一个是α=2的高斯过程,另一个是α< 2 的稳定过程。而在大气噪声中,往往是α<2的稳定过程表达得多,占了主要的部分。因此,不妨先假设接收到的数据{xk}满足α<2的稳定过程,首先估计参数α和γ,然后在估计高斯分量的δG。
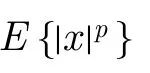
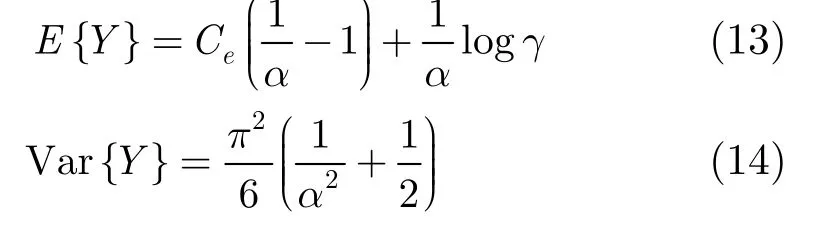
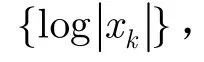
观察大气噪声数据中,其非高斯特性的表达主要由高幅度的脉冲体现出来。若将高幅度脉冲数据剔除掉,那么其非高斯特征就会减弱。因此,设f0.75(xk)为75%分位点,取xk<f0.75(xk)的所有值,并计算其方差,即可得到估计值σ2。由于在其中包含了非高斯部分的表达,σ2的值会高于。进一步扣除掉非高斯噪声的能量,有 =σ2-2γ(α稳定过程γ相当于高斯过程中的/2),这样就能较好地初步估计出了高斯分量的δG。
解决了迭代的初始值估计,还有存在{λk}序列选取的问题。由于实际中一般可以假设收到的大气噪声数据服从对称分布,因此有
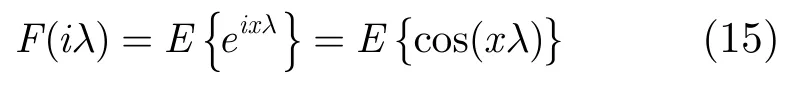
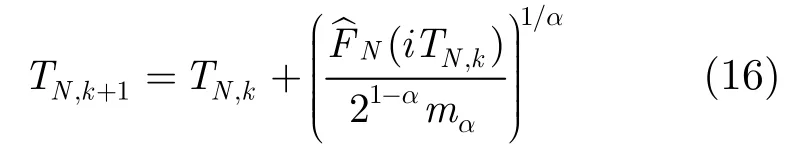
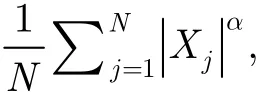
下面我们引入定理[10]:
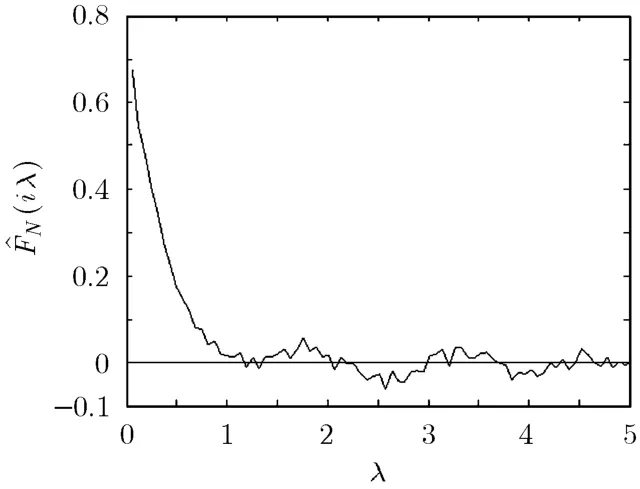
图1 N (i λ )的零点摆动现象
定理1对于任意固定值N<∞,当k→∞时,有TN,k→AN。(证明从略)
因此,只要构造足够长的序列{TN,k},就可以无限逼近AN。在实际中,为了计算方便,可以取α= 1 。只要获得了AN的值,就可通过将区间(0,AN)划分为T等分,来构造序列{λk|λk=k(AN/T),k=1,…,T} 。
5 仿真及实际结果
在本文中统计的参数为θ= {α,γ,δG} ={θ1,θ2,θ3} 。由于Class B噪声模型可以看成是对称α稳定过程(Sα S)和独立高斯过程(G)的混和模型。因此噪声的产生由两个噪声源相加,一个Sα S噪声源,利用文献[11]中的方法产生;另一个是高斯噪声源。一般地,以均平方相对错误率(MSNRE)作为标准,即
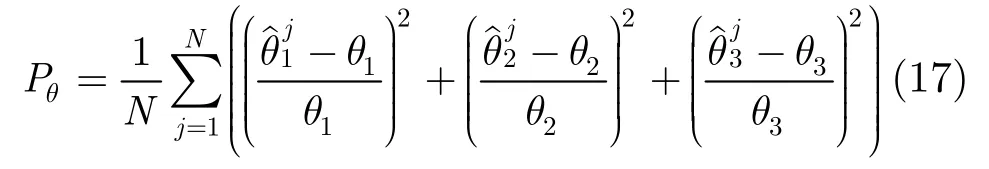
其中此时的N为仿真实验次数,θi为第i个参数实际值,为第j次实验第i个参数的估计值。
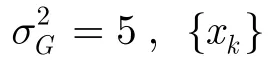
在仿真实验中,设置α=0.5,γ=2,= 5 ,{λk}的长度为T为40。每次实验运行100次。当观测数据长度K为2500时,图2为经验曲线、理论曲线以及估计曲线三者关系的示意图,X轴为λ的值,Y轴为lnF(iλ),其中经验曲线通过FN(iλ)的估计获得。可以看到,本文提出的方案估计出的参数与实际参数有很高的一致性。如图3所示,当观测数据长度为1000, 2500, 5000时,迭代次数同MSNRE的关系图。数据表明,本方案迭代次数少,一般都能在10次迭代中得到收敛,同时从图中容易观察到随着数据长度的增加,迭代的精度也随之增加。

表1 α的初步估计值
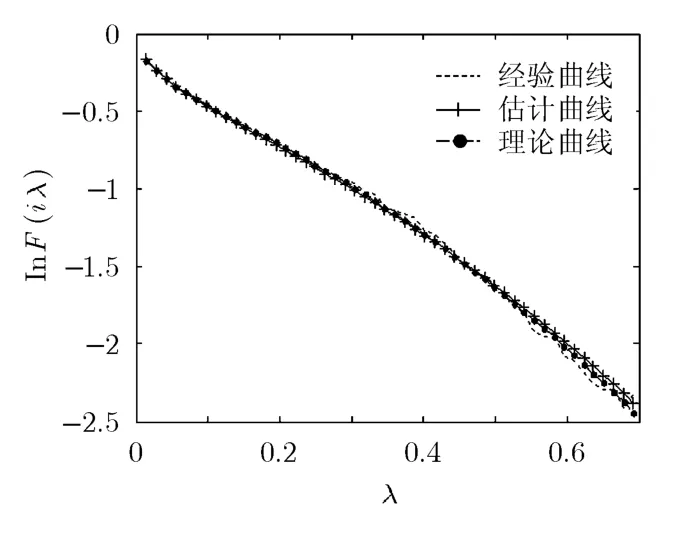
图2 经验曲线,估计曲线及理论曲线关系
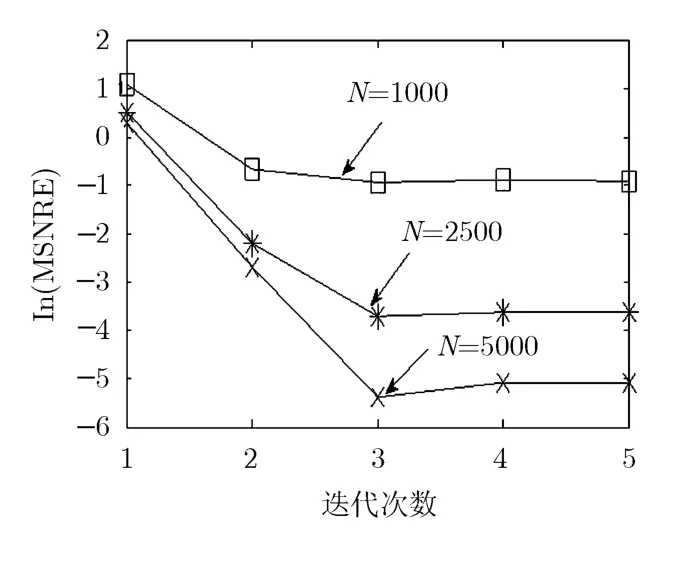
图3 不同数据长度对MSNRE的影响
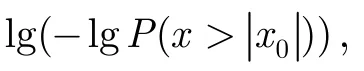
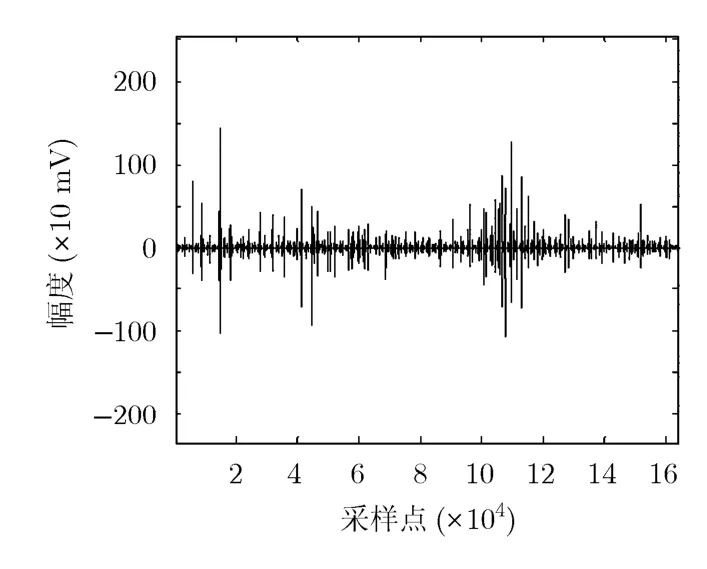
图4 大气噪声信号
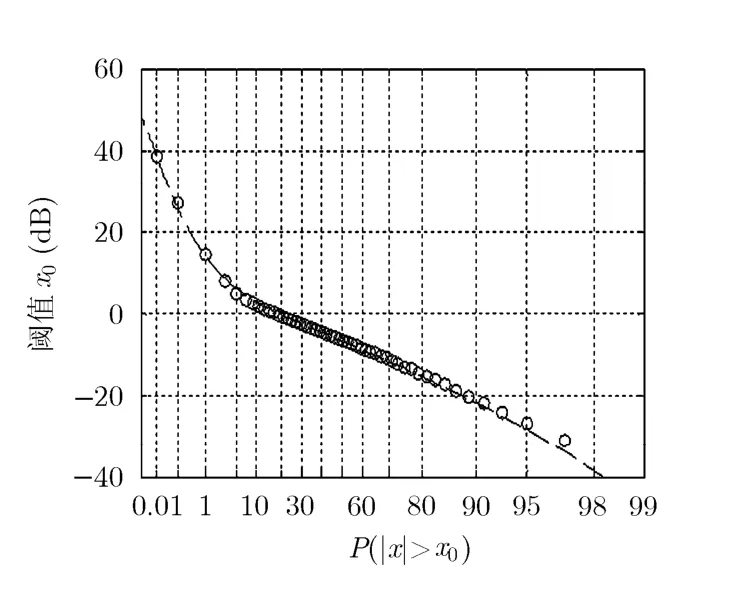
图5 实测数据及估计结果的APD
6 结论
通过对Class B噪声模型的研究,本为提出了一种利用非线性回归模型估计Class B噪声模型的方法。由于概率密度函数表达式复杂且收敛慢等因素,本文从特征函数出发,推导了非线性回归模型,并优化了迭代算法,使其加快了收敛速度并减少迭代次数。特别地,利用Class B模型的特殊性,设计了初始值估计方案。同时,分析实际中情况,设计了{λk}选取的方案。最后仿真结果及实测数据的估计结果表明,本文提出的算法收敛快,精度高,估计出的参数能很好地反映实际情况。本文的研究结果对超低频非高斯噪声信道的检测和估计具有较重要的理论和实际意义。
[1]Abraham D A. Detection threshold approximation for non-Gaussian backgrounds[J].IEEE Journal of OceanicEngineering, 2010, 35(8): 335-341.
[2]许玲, 靳致文, 王西乾. SLF/ULF大气噪声谱密度全球分布预测[J]. 电波科学学报, 2010, 25(4): 773-778.
Xu Ling, Jin Zhi-wen, and Wang Xi-qian. Estimation of SLF/ULF noise global distribution[J].Chinese Journal of Radio Science, 2010, 25(4): 773-778.
[3]Goken C, Gezici S, and Arikan O. Optimal signaling and detector design for power-constrained binary communications systems over non-Gaussian channels[J].IEEE Communications Letters, 2010, 14(2): 100-102.
[4]蒋宇中. 非高斯噪声中的 Turbo码的性能改进研究[J]. 应用科学学报, 2006, 24(4): 336-340.
Jiang Yu-zhong. Performance improvement of Turbo code in non-Gaussian noise[J].Journal of Applied Science, 2006,24(4): 336-340.
[5]Rosado-Munoz A. FPGA implementation of an adaptive filter robust to impulsive noise: two approaches [J].IEEE Transactions on Industrial Electronics, 2011, 58(3): 860-870.
[6]Middleton D. Statistical-physical models of electromagnetic interference[J].IEEE Transactions on Electromagnet Compact, 1977, 19(5): 106-127.
[7]Middleton D. Non-Gaussian noise models in signal processing for telecommunications: new methods and results for Class A and Class B noise models[J].IEEE Transactions on Information Theory, 1999, 45(4): 1129-1149.
[8]Nikias C L and Shao M. Signal Processing with Alpha-Stable Distribution and Applications[M]. New York: Wiley, 1995.
[9]Khalil H K. Performance of an optimal receiver in the presence of alpha-stable and Gaussian noises[J].IEEE Statistical Signal Processing Workshop(SSP), 2011, 56(8):573-576.
[10]Welsh A H. Implementing empirical characteristic function procedures[J].Statistics and Probabilitys Letters, 1986, 4(7):65-67.
[11]Chambers J M, Mallows C L, and Stuck B W. A method for simulation stable random [J].Variables, Journal of American Statistical Association, 1976, 71(5): 340-344.

