分布作用速调管大信号计算模型的研究
黄传禄 丁耀根 王 勇 谢兴娟②
①(中国科学院电子学研究所中国科学院高功率微波源与技术重点实验室 北京 100190)
②(中国科学院研究生院 北京 100039)
1 引言
分布作用速调管(EIK)作为一种新型微波器件,与传统速调管相比,在高频段具有频带宽,效率高的优点。其高频结构采用多间隙耦合腔,以提高注波互作用效率,并增加了带宽[1,2]。速调管中电子注与电磁场的相互作用,包括间隙中电子注与高频场的互作用、以及电子注在自身空间电荷场作用下的群聚等过程是速调管的主要物理过程。这些物理过程对系统的效率和带宽等工作特性具有直接影响。注波互作用过程的计算机模拟[3-6],对于速调管快速准确的设计与制造具有重要意义。利用空间电荷波小信号理论[7],以及微波网络等效分析的方法,可以得到群聚段小信号下的增益频宽等特性,但对于输出腔等非线性段的注波互作用却无法准确分析[2]。分布作用速调管的注波互作用大信号模拟在目前尚没有合适的计算模型和软件工具。现有的大多数速调管注波互作用模拟软件,无论是基于传统的一维电子圆盘模型[3],还是2.5维的圆环模型[5],乃至利用PIC粒子方法的互作用模型[4,6]都不能有效地模拟分布作用速调管。在实际模拟中需要将多间隙耦合腔等效为单间隙腔,但这种等效掩盖了很多物理事实,例如多间隙中高频场的场型模式分布,以及耦合腔的稳定性[8]等。全时域的3D粒子模拟软件[9],虽然可以直接由边界条件模拟任意间隙情况,但由于其使用复杂,计算时间长,计算资源要求高,其应用具有局限性,无法普遍应用。为开展分布作用速调管的研究,需要发展一种能快速,方便计算EIK注波互作用的大信号计算模型。
本文基于一维电子圆盘模型,采用时间积分的方式建立分布作用速调管注波互作用的大信号计算模型,发展了基于这种模型的用于双间隙耦合腔的计算程序,并与文献[9]中的EIK实例仿真结果进行了比较验证。利用程序计算分析了双间隙耦合腔注波互作用特性,并扩展到更多间隙情形。另外对程序在计算速度、稳定性以及扩展到2维圆环模型等方面进行了分析。
2 物理模型
2.1 电子圆盘运动方程
根据一维电子圆盘模型,电子圆盘在高频电场和空间电荷场作用下的相对论运动方程[2]为
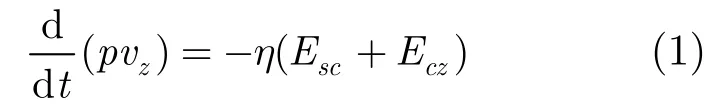
其中p= [ 1 - (vz/c)2]-1/2为相对论因子,c为光速;η=e/m0为电子荷质比;Esc为电子圆盘受到的空间电荷场;Ecz为作用在电子圆盘上的高频电场。
进行时间和轴向距离归一化:τ=ft,y=fz/v0,其中f为工作频率,v0为电子直流速度。则电子圆盘的运动方程归一化形式为
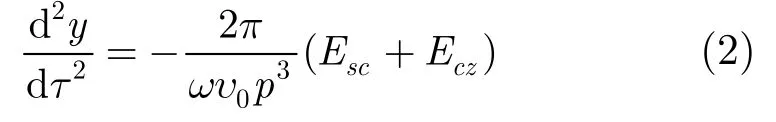
该方程离散后化为差分方程,可以用龙格-库塔法求解。
2.2 空间电荷力的计算
根据电子圆盘模型,采用静电场格林函数法[7],可以得到一个电子圆盘受到一个高频周期内其它所有电子圆盘的空间电荷作用力的总和。
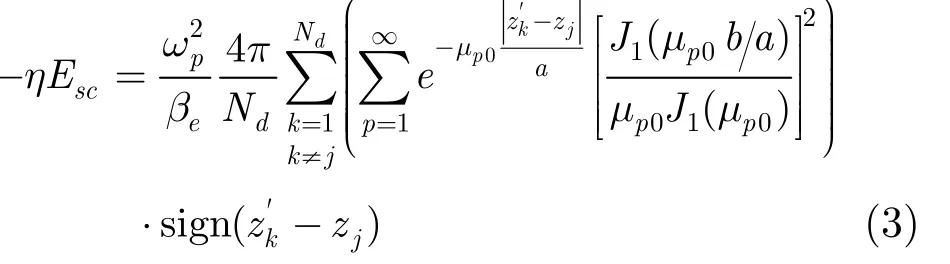
式(3)表示位于zj的电子圆盘受到位于zk(k=1:Nd,k≠j)的电子圆盘的库仑作用力。其中,Nd为一个高频周期内划分的电子圆盘数,ωp为等离子体角频率,βe为电子纵向传播常数。b为电子注半径,a为漂移管半径,μp0为零阶贝塞尔函数的第p个根,J1(x)为一阶贝塞尔函数。sign(x)为符号函数,x> 0 时,sign(x) = 1;x<0时,sign(x) = - 1。
2.3 间隙高频电场的计算
谐振腔单个间隙电场由间隙电压和场型分布函数得到[3]
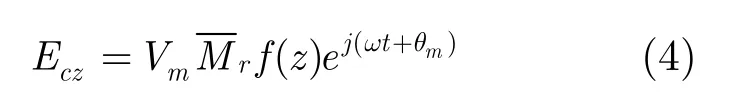
式(4)中Vm是间隙电压幅值,θm为相位。Mr为径向耦合系数,是间隙电场对电子注截面取平均的结果。f(z)是高频场型函数,在本模型中使用高斯分布函数[3]。
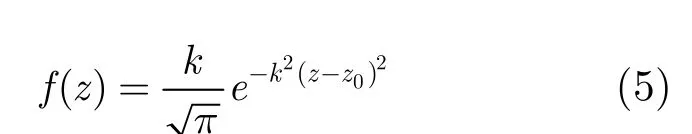
其中k= (a2-b2+δd2)-1/2,δ的取值反映了漂移头形状对场型的影响,一般取1/4~1/6。
利用上面单间隙场型分布形式,双间隙耦合腔的间隙电场可描述为
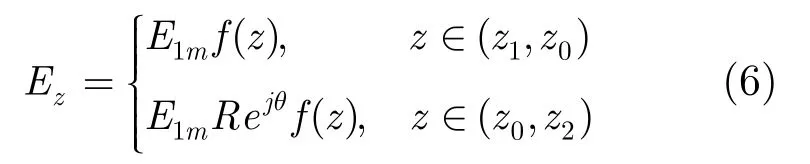
式(6)中E1m为耦合腔间隙 1电场幅值;R,θ分别为间隙2电场与间隙1电场的幅度之比与相位差。对于2π模式,R=1,θ=0;对于π模式,R=1,θ=π。 (z1,z0)为间隙1电场区域, (z0,z2)为间隙2电场区域。
2.4 双间隙耦合腔等效电路模型
双间隙耦合腔间隙的电子注与高频电场的互作用过程,是通过如图1的等效电路[2]实现的。电子注(电子圆盘)由于运动而在间隙上产生感应电流,通过等效电路网络产生间隙电压,从而形成间隙电场,并反作用于电子注,影响其运动状态。这样相互作用经过迭代达到稳定状态,便是注波互作用模拟的主要过程。
图1中元件参数由耦合腔的冷测参数,如谐振频率f、特征阻抗R/Q、品质因数Q等得到,其中G1,G2分别为两个耦合腔的损耗电导,包括腔体损耗电导与电子电导。由图1可以得到电路的阻抗矩阵。电路的感应电压由感应电流基波分量与阻抗矩阵相乘得到:
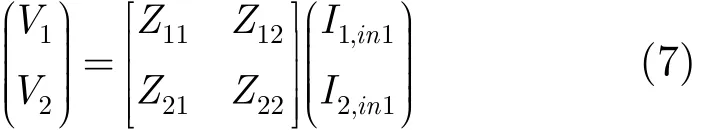
式(7)中的间隙感应电流根据拉姆定律由式(8)求得[2]。
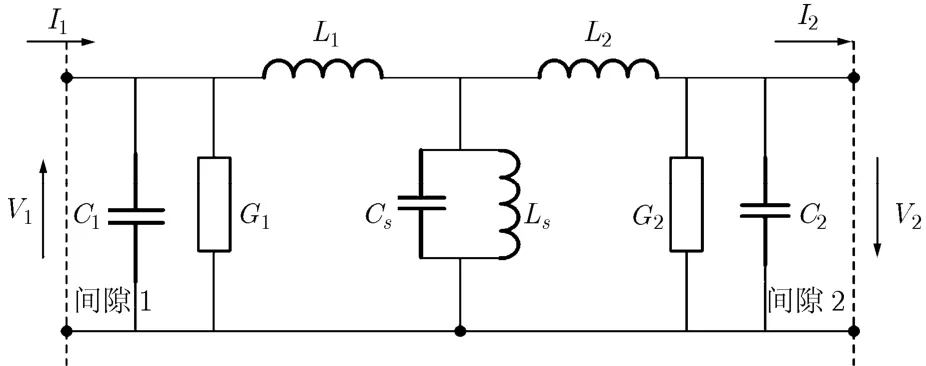
图1 基于TM010模式的双间隙耦合腔等效电路
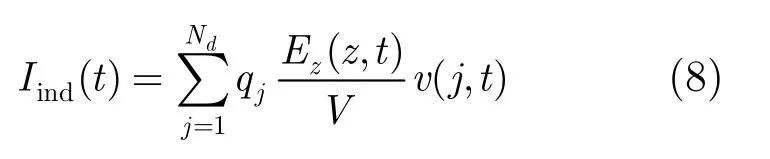
qj为电子圆盘的电量,Ez为间隙电场,V为间隙电压幅值,v为电子圆盘的运动速度。将感应电流进行傅里叶级数展开,即得到各次谐波的感应电流分量。
2.5 双间隙阻抗矩阵中电子电导计算
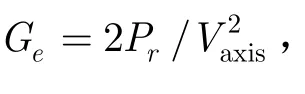
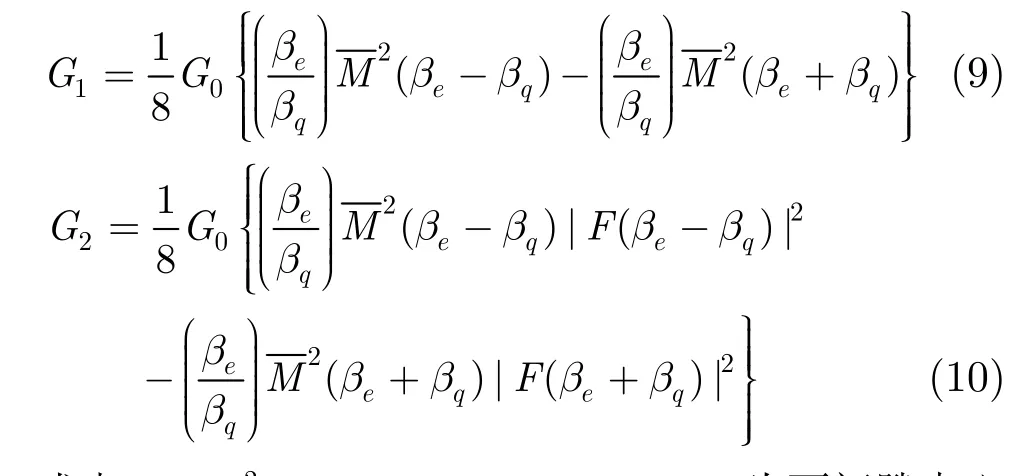
式中 |F(x) |2= 1 + 2 cos(θ+Px) /R。P为两间隙中心距离。R,θ的意义同式(6)定义。M(βe-βq),M(βe+βq)分别是对应快波与慢波的单间隙耦合系数。βe为电子传播常数,βp为对应的等离子传播常数。βq=Fβp,F为等离子体频率缩减因子。
2.6 计算程序流程
依据上面物理模型编写了模拟程序,程序采用超松弛迭代法[2],比较前后两次得到的间隙电压是否收敛。由于前面群聚段属于小信号,相比较后面的非线性段容易收敛,所以程序设计采用从输入腔到输出腔依次判别收敛,对于已经收敛的谐振腔,不再进行迭代计算。这样可以有效的节省计算时间,提高计算速度。图2是程序的架构流程图。
3 计算结果
利用编写的大信号计算程序,以文献[9]中的EIK实例做了相应的计算模拟,与文献的仿真结果进行了对比。文献中给出了利用粒子仿真软件MAGIC3D得到的模拟结果。该实例为 Ka波段EIK,中心频率35 GHz。其高频结构共7个谐振腔,除末前腔外,其余均采用双间隙耦合腔。其设计输出功率为1 kW,增益为35 dB,效率为17.8%, 3 dB带宽为200 MHz。电子注电压14 kV,电流0.4 A。
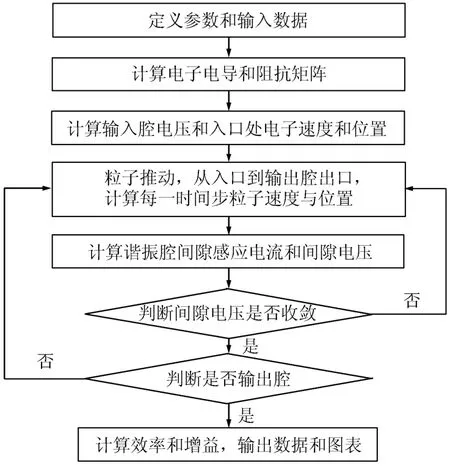
图2 计算程序流程
双间隙耦合腔的电场通过耦合槽和漂移管相互耦合[2,9],目前并没有准确的解析模型描述其电场分布。式(6)的场型分布中用到的高斯函数(式(5))是依照于单间隙情况,无法考虑到由于相互耦合而造成的场型变化。除了解析场型外,还可以利用高频软件计算出场型分布,然后以文件格式导入程序中,但这样做非常繁琐,不符合程序设计的初衷。对于1维程序,由于仅考虑轴向电场,两间隙相互耦合对其影响相对不大,所以在程序中采用高斯函数合成(式(6))来模拟耦合腔间隙场型分布。图3为采用式(6)的双间隙场型分布与高频软件仿真的场型分布的比较。模型采用2π模式,场型为距离归一化形式。从图中可以看出,对于轴线上的轴向电场分布,在两间隙中心左右,解析场型和仿真场型非常接近,而在两间隙之间的漂移段,仿真结果有电场的分布,而解析场型由于没有考虑耦合的情况,所以没有电场分布。但这方面的差别,对1维情况来说影响很小,可以不考虑。
图4是在中心频点(35 GHz)上的输出功率随输入功率的变化趋势图。可以看出,1维模型计算结果与文献中MAGIC3D结果变化趋势一致。两仿真结果的饱和激励点比较一致,都在0.3 W左右。图5 是在固定激励(0.25 W)点上输出增益随频率变化趋势图,图中两者的增益-频率特性比较符合一致。两仿真结果的3 dB增益带宽也比较符合,从图中可以看出3 dB带宽能达到200 MHz左右。
从图 4,图 5两图还可以看出,利用模型仿真得到的功率或增益明显高于用粒子仿真软件MAGIC3D得到的结果。这是由于本文模型是基于1维理论,假设磁场无限大,不考虑径向分量变化,忽略了电子注的径向波动,截获等不利影响[2,5,9],所以结果普遍高于2维乃至3维仿真结果。
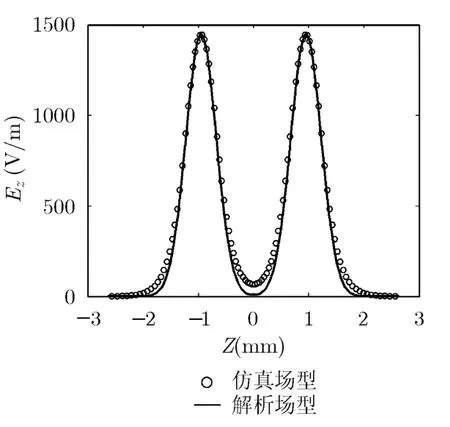
图3 双间隙耦合腔间隙场型分布
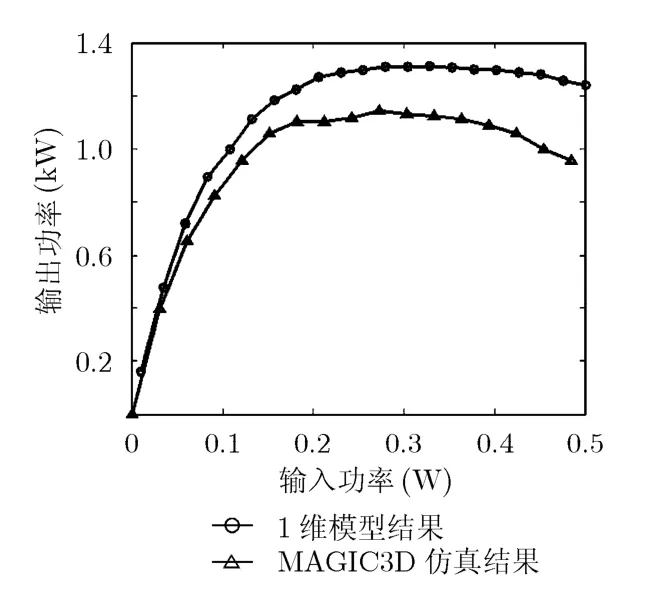
图4 输出功率仿真结果图
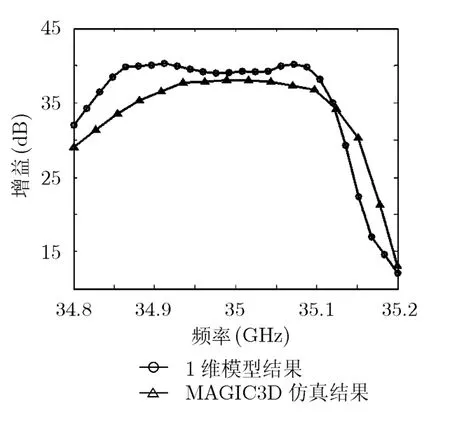
图5 增益-频率特性
利用本文模型编写的程序,计算时间短,计算资源要求少,可以快速地给出输出功率、效率、增益等特性参数。用本文的EIK实例,进行单频单激励点计算,经过对比验证,得到本模型程序计算时间小于10 s,等效成单间隙腔后利用其他2.5D程序,大概需要十几分钟,而利用MAGIC3D则需要将近35个小时。在内存等资源消耗方面,本文程序也远远小于其它计算程序。尽管本文1维程序计算结果普遍高于2维乃至3维结果,但其反映的特性曲线变化趋势正确,并且计算速度快,对于速调管初始参数的设计、确定谐振腔的位置、频率偏谐等仍具有重要的参考意义。本文模型还可以采用 2.5维圆环模型,便能考虑径向分量变化,电子截获等物理事实,从而可以得到更加准确的模拟结果。
根据速调管群聚理论[7],电子注在线性段群聚电流很小,群聚相位变化也很小,在非线性段群聚电流迅速增加,相位变化剧烈,不再满足稳相条件。在输出间隙应使群聚电流达到最大值,以保证最大的输出效率。从群聚电流分布,以及电子的群聚相空间图可以看出互作用情况的好坏,检验参数设计的合理性。图6 是在中心频点处电子注的归一化群聚电流(Ib/I0)的轴向分布图,在群聚段,运动电流很小,在后面增益区,群聚电流,尤其是基波分量,随距离迅速增大,在输出间隙位置达到最大值。图7 是对应的归一化相空间群聚图,由此图也可以看出输出腔电子群聚明显,能量交换剧烈。这说明该模型能正确反映注波互作用中电子群聚的物理过程[7]。
4 结束语
本文基于1维圆盘模型发展了一种可用于模拟分布作用速调管注波互作用的大信号计算模型,并编制了相应的计算机程序。通过对文献相关数据的验证,可以看出这个模型能有效地反映注波互作用的基本物理过程。但1维模型没有考虑径向电场分量和磁场,不能完全反映物理事实,如电子注径向波动和截获等情况,得到的计算结果普遍高于2维与3维仿真结果。对于双间隙高频电场分布的解析方法也没有考虑到其存在的耦合情况,这不可避免的带来计算误差。尽管如此,该模型及计算程序执行效率高,计算速度快,计算结果对器件设计的初步参数具有重要意义。本文模型还可以采用更加精确的2维圆盘模型,同时对进一步发展其他EIK注波互作用计算模型也具有参考意义。
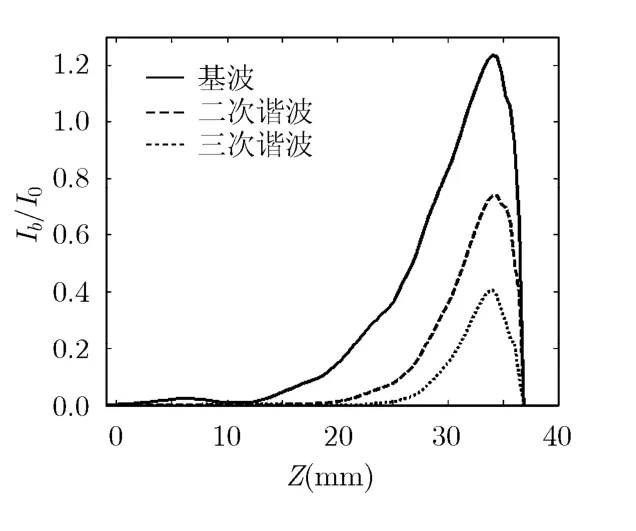
图6 群聚电流轴向分布
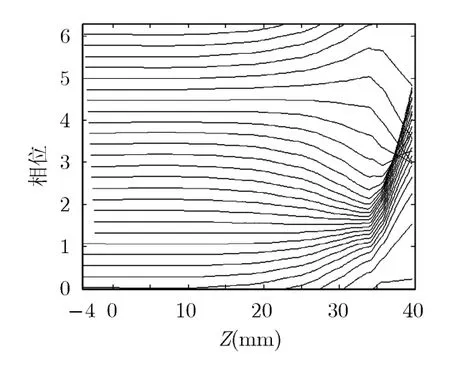
图7 群聚相空间图
[1]Chodorow M and Wessel-berg T. A high-efficiency klystron with distributed interaction [J].IEEE Transactions on Electron Devices, 1961, 8(1): 44-55.
[2]丁耀根. 大功率速调管的理论与计算模拟[M]. 北京: 国防工业出版社, 2008: 95-100.
Ding Yao-gen.Theory and Computer Simulation of High Power Klystron [M]. Beijing: National Defense Industry Press,2008: 95-100.
[3]Yonezawa H and Okazaki Y. A one-dimension disk model simulation for klystron design [R]. SLAC-TN-84-5, 1984.
[4]Gao Dong-ping, Du Chao-hai,et al.. Develop a 2.5-dimensional particle-in-cell code for efficient high-power klystron design [J].IEEE Transactions on Plasma Science,2010, 38(6): 88-96.
[5]赵鼎. 速调管非线性注波互作用程序的研究[D]. [博士论文],中国科学院电子学研究所, 2007.
Zhao Ding. Research on nonlinear beam-wave interaction program for klystrons [D]. [Ph. D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2007.
[6]高冬平, 丁耀根, 等. 基于速调管 2.5维粒子模型的非线性注波互作用的研究[J]. 电子与信息学报, 2010, 32(10):2490-2495.
Gao Dong-ping, Ding Yao-gen,et al.. The nonlinear beam-wave interaction of high power klystrons based on a 2.5-dimensional particle-in-cell model [J].Journal of Electronics&Information Technology, 2010, 32(10):2490-2495.
[7]谢家麟, 赵永翔. 速调管群聚理论[M]. 北京: 科学出版社,1965: 88-93, 128.
Xie Jia-lin and Zhao Yong-xiang. Bunching Theory of Klystrons [M]. Beijing: Science Press, 1965: 88-93, 128.
[8]全亚民. 速调管的稳定性问题研究[D]. [博士论文], 中国科学院电子学研究所, 2008.
Quan Ya-min. Research on the stability of a klystron [D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2008.
[9]Hsu H. Introduction of design and 3D computer modeling of a Ka-band EIK[D]. [Ph.D. dissertation], University of California Davis, 2006.
[10]全亚民, 丁耀根, 王树忠, 等. 多注双间隙耦合腔电子电导计算与模拟[J]. 电子与信息学报, 2009, 31(5): 1214-1217.
Quan Ya-min, Ding Yao-gen, Wang Shu-zhong,et al..Calculation and simulation of the electronic conductance in double gap coupling MBK cavity [J].Journal of Electronics&Information Technology, 2009, 31(5): 1214-1217.
[11]黄传禄, 丁耀根, 王勇. 双间隙耦合腔电子电导的理论与计算仿真[J]. 物理学报, 2011, 60(12): 128401.
Huang Chuan-lu, Ding Yao-gen, and Wang Yong. The theory and computer simulation of beam-loading conductance in the double-gap slot-coupled cavity [J].Acta Physica Sinica,2011,60(12): 128401.

