基于霍夫变换的高速微弱目标检测算法
庞存锁 侯慧玲 韩 焱
(中北大学电子测试技术国家重点实验室仪器科学与动态测试教育部重点实验室 太原 030051)
1 引言
随着科学技术的发展,尤其是隐身技术和超音速技术的日渐成熟,具有隐身和高速性能的飞行器越来越多,研究提高传统雷达对高速微弱目标检测能力的信号处理方法具有重要意义。为了检测高速微弱目标,长时间相参积累技术是一种有效方法[1],但长时间积累导致目标回波包络在不同脉冲周期之间走动,传统的基于单元的动目标检测方法已不能有效适应该类目标的检测,需在检测前进行回波包络对齐。针对包络对齐的问题已经有不少研究,文献[2-4]研究了包络移位和包络插值的包络对齐方法;文献[5-8]研究了基于Keystone变换的包络对齐方法,但该方法存在速度模糊;文献[9]研究了基于脉冲压缩前的距离走动补偿方法,但存在补偿通道多的问题。文献[10]利用最大似然准则的方法研究了包络对齐,并提出利用霍夫变换的方法估计高速目标的思想,但文中没有分析HT的具体运算过程,且存在运算量大的问题。
以上研究方法虽然能够实现包络对齐,但运算量大,实时性差。为此,本文以线性调频脉冲压缩雷达为例,提出了一种并行HT(PHT)方法,此方法利用叠加原理能够提高运算速度,满足实时性的要求;最后给出了仿真实例,仿真结果表明了算法的有效性。
2 高速目标回波信号特点
针对线性调频脉冲压缩雷达,根据文献[9, 10]可得第n个回波信号的包络时延走动Δtn与目标速度、加速度等有关,可表示为

(1)b0nPRT表示由速度引起的第n个脉冲相对于第1个脉冲的走动时延,其导致的距离走动单元为
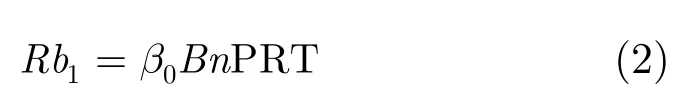
(2)a/c(nP RT)2表示由加速度引起的第n个脉冲相对于第1个脉冲的走动时延,其导致的距离走动单元为
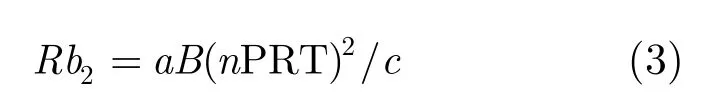
需注意通常加速度引起的距离走动可以忽略,如信号带宽为5 MHz,停留时间为0.5 s,根据式(3)知加速度要想产生 1个距离单元的走动需大于240 m/s2,一般目标的加速度不可能达到这么大,故可忽略其对距离走动的影响。因此,高速目标回波间的距离走动主要由速度引起,且走动单元与积累时间近似为直线。
3 基于HT的高速目标检测
3.1 HT检测高速目标速度和距离的基本原理
高速目标回波信号离散采样后,其目标速度v0,距离R0与直线斜率k、截距b的关系可表示为

根据式(4),式(5)可得目标初始距离,径向速度与极径,极角间的关系为

其中v0<0表示目标接近雷达,v0>0表示目标远离雷达,fs为采样频率, (r0,q0)为HT后最大值对应的极坐标值。
3.2 极径ρ和极角θ的量化间隔
从高速目标的回波特点出发,我们推导了极径量化间隔Δr,极角量化间隔Δq的值。
由文献[9]可得搜索未知高速目标时的速度间隔可表示为

其中BNT为发射信号带宽与积累脉冲时间的乘积。
将式(8)代入式(4),式(6)可得 Δq为
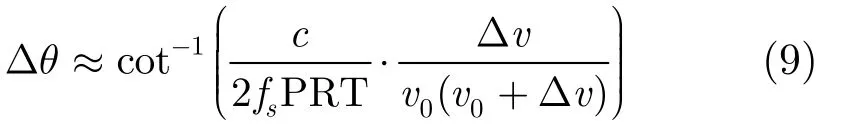
假定高速目标回波脉冲间的距离走动单元最大不超过一个距离分辨单元,可得Δr为
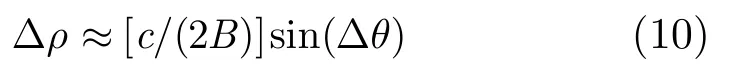
3.3 一种基于并行运算的HT方法(PHT)
HT虽能够检测直线,但文献[10]中的方法运算量大,难以满足实际应用。这里借鉴文献[11]中计算HT的思想对目标回波矩阵进行处理。
(1)PHT原理
引理利用如图1所示的PHT几何关系,可得

证明如图 1(a)所示,设l为穿过坐标系XoY中A点的直线,ro(A,q)为从原点o到l的垂线,q为垂线和坐标轴X的夹角。o'点为数据矩阵中的另一点,ro(o',q)为从原点o到h的垂线,这里设h为穿过o'点的直线,且h||l,ro'(A,q)为从o'点到l的垂线,其对应的坐标系为xo'y,如图1(b)所示。
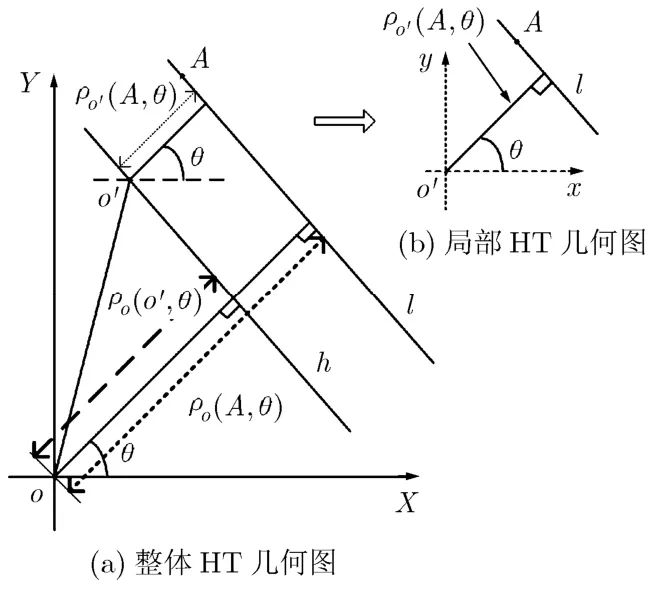
图1 PHT几何关系图
由HT 的定义可得,坐标系XoY中A点,o'点相对于原点o的HT可分别表示为


在图1(b)坐标系xo'y中,A点相对于点o'的HT可分别表示为
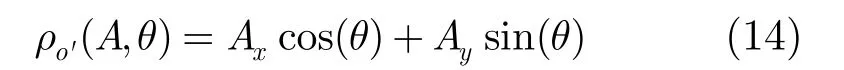
其中(Ax,Ay) 为点A在坐标系xo'y中的坐标。
由图1几何关系及式(12)-式(14)可得
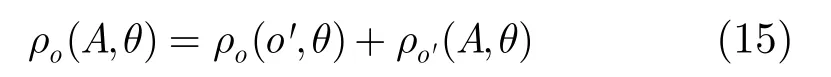
式(15)也可表示为式(11)的形式,这一方法可推广为直线上某一点关于坐标原点的HT可用任意多个点HT的叠加表示。因此,该方法利于并行运算,可减小HT的运算时间。
(2)PHT的应用 式(15)证明了点的HT叠加原理,这一部分将讨论该原理在雷达回波矩阵中的应用。
为了应用该原理,需对回波矩阵进行子矩阵分解。设雷达回波矩阵[M,N]可分为k1×k2组子矩阵,即[M,N]可表示为

由式(15),式(16)可得k1×k2组子矩阵的并行HT叠加过程可表示为
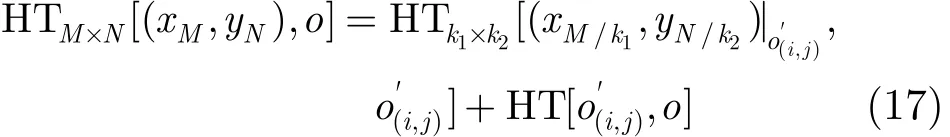
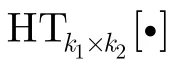
另外,由式(15)可知,如果 HT处理的回波矩阵能分解为大小相等的几组子矩阵,则每组子矩阵中相同位置点的 HT相同,则式(17)可进一步表示为
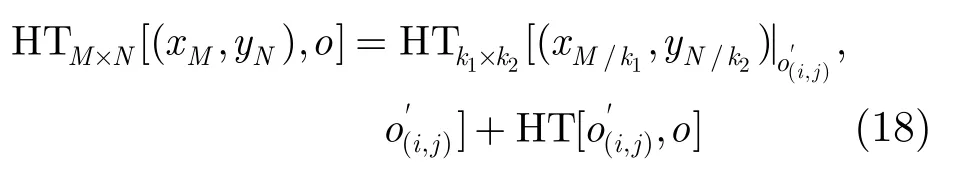
式(18)的这一性质可节约存储空间并能提高 HT计算效率。
4 仿真实例
设观测目标相对于雷达的初始距离为100 km,径向速度为3000 m/s,加速度为5 m/s2,信号载频为3 GHz,基带信号带宽为5 MHz,积累脉冲数为128,脉冲重复周期为1 ms,采样频率为10 MHz,脉冲宽度为0.1 ms,噪声为复高斯白噪声。
4.1 PHT对高速目标的检测流程
根据上述参数,由式(16)可把回波矩阵[M,N]分为4个165×64的子矩阵,其中行代表目标的距离单元数,列代表回波脉冲数。图2为PHT对4个子阵的执行过程。图 2(a)为采用文献[10]方法处理的结果,图2(b)为采用PHT处理过程。 从图2(b)可看出,子阵I,II,IV中3维图的峰值比较明显,且对应的 2维投影交点位置相同,这与直线l分布在图2(a)中I,II,IV区的情况相吻合。图2(c)为4个子阵执行PHT后的3维显示结果,与图2(a)处理结果相同,验证了PHT的正确性。
4.2 PHT检测性能
为了验证算法性能,本节采用峰值检测方法比较了文献[4]中包络插值,文献[7]中Keystone及本文算法在不同信噪比下对目标初始距离、径向速度的检测概率。经过200次Monte Carlo仿真实验,从图3可看出包络插值和Keystone算法检测性能基本一致,在信噪比低于-40 dB时,检测性能略高于本文方法,这是由于本文算法为了减少搜索次数所取量化间隔略大于其它两种方法。图4给出了目标在不同速度下本文方法与包络插值方法复乘次数的比较,从图4可看出包络插值与本文算法所用的复乘次数在一个数量级上,但本文方法采用了分解并行运算,故运算时间比包络插值约低4倍,且随着分解子矩阵的增多,可进一步提高运算速度,满足实际应用。

图2 PHT的执行过程示意图

图3 3种算法检测性能比较

图4 包络插值和HT算法复乘次数比较
5 结论
目标高速运动引起回波在脉冲间走动,影响雷达检测性能。本文提出了一种并行HT的高速目标检测方法,该方法适合于对高加速目标进行检测,同时能提高算法的实时性。文中结合实际应用,仿真比较了并行HT方法与包络插值、Keystone方法对高速目标的检测性能,指出在检测性能相同的情况下,本文方法复乘次数较其它方法少,且随着分解子矩阵的增多,可进一步减少运算时间。
[1]张月, 邹江威, 陈曾平. 泛探雷达长时间相参积累目标检测方法研究[J]. 国防科技大学学报, 2010, 32(6): 15-20.
Zhang Yue, Zou Jiang-wei, and Chen Zeng-ping. Long-time coherent integration targets detection method for ubiquitous radar[J].Journal of National University of Defense Technology, 2010, 32(6): 15-20.
[2]Chen C and Andrews H C. Target-motion-induced radar imaging [J].IEEE Transactions on Aerospace and Electronic Systems, 1980, 16(1): 2-14.
[3]Wang K, Luo L, and Bao Z. Global optimum method for motion compensation in ISAR imagery[C]. Proceeding Conference Radar’97, Edinburgh, UK, 1997(10): 233-235.
[4]Wang G Y and Bao Z. The minimum entropy criterion of range alignment in ISAR motion compensation[C].Proceeding Conference Radar’97, Edinburgh, UK, 1997(10):236-239.
[5]Perry R P, DiPietro R C, and Fante R L. SAR imaging of moving targets [J].IEEE Transactions on Aerospace andElectronic Systems, 1999, 35(1): 188-200.
[6]Zhu D, Li Y, and Zhu Z. A keystone transform without interpolation for SAR ground moving-target imaging [J].IEEE Geoscience and Remote Sensing Letters, 2007, 4(1):18-22.
[7]苏军海, 刑孟道, 保铮. 宽带机动目标检测[J]. 电子与信息学报, 2009, 31(6): 1283-1287.
Su Jun-hai, Xing Meng-dao, and Bao Zheng. Wideband radar detection for maneuvering target[J].Journal of Electronics&Information Technology, 2009, 31(6): 1283-1287.
[8]秦国栋, 陈伯孝, 陈多芳, 等. 一种多载频MIMO雷达高速运动目标多维参数估计方法[J]. 电子学报, 2010, 38(12):2763-2768.
Qin Guo-dong, Chen Bai-xiao, Chen Duo-fang,et al.. A method of multiple parameters estimation for high speed moving targets in multi-carrier-frequency MIMO radar[J].Acta Electronica Sinica, 2010, 38(12): 2763-2768.
[9]Tao R, Zhang N, and Wang Y. Analysing and compensating the effects of range and Doppler frequency migrations in linear frequency modulation pulse compression radar [J].IET Radar,Sonar&Navigation, 2011, 5(1): 12-22.
[10]Theagenis J A and Gregory O G. Range, radial velocity, and acceleration MLE using radar LFM pulse train [J].IEEE Transactions on Aerospace and Electronic Systems, 1998,34(4): 1070-1084.
[11]Satzoda R K, Suchitra S, and Srikanthan T. Parallelizing the Hough transform computation [J].IEEE Signal Processing Letters, 2008, 15(2): 297-300.

