60 GHz毫米波通信中一种新的波束搜索算法
邹卫霞 杜光龙 李 斌 崔志芳 胡玉聪 张 芳
(泛网无线通信教育部重点实验室 北京 100876)
(北京邮电大学无线网络实验室 北京 100876)
1 引言
随着多媒体应用业务的不断发展,无线通信应用对传输速率的需求与日俱增,目前无线局域网(Wireless Local Area Networks, WLANs)和无线个域网(Wireless Personal Area Networks, WPANs)所能提供的数百Mbps峰值传输速率已然难以满足应用需求[1]。在此趋势的推动之下,能提供Gbps传输速率的60 GHz无线通信以绝对优势脱颖而出,在全球范围内受到广泛关注[2]。60 GHz频段隶属于毫米波(millimeter-wave),占据约2 GHz带宽[3-6],适合于高速、短距离通信场景。同时,由于其波长甚短,亦使多天线系统易于集成实现,进而可利用波束赋形技术(beam-forming)改善传输质量,提升系统容量[7]。作为60 GHz通信系统的一个显著优势,波束赋形技术已应用于目前60 GHz相关标准中,例如 IEEE 802.15.3c[5]和 802.11ad[6]。
波束赋形技术通常分为自适应阵列天线系统(adaptive-array system)和固定波束切换系统(switched-beam system)[8,9]。鉴于实现复杂度及功率消耗等因素,60 GHz通信系统通常倾向于采用后者,即预先设计好一组备选用波束模式的天线加权向量(beam steering vector)或者称为波束码本(beam codebook),在实际数据传输时,从码本中选取最优波束进行通信[3,10,11]。因此,区别于传统意义波束赋形,可将60 GHz通信系统中波束赋形称为波束搜索(beam searching)。目前为止,有关波束搜索算法的文献相对较少,仅在已制定的 IEEE 802.15.3c标准以及正在制定的IEEE 802.11ad标准草案中进行了初步研究。这两个标准中的波束搜索算法均基于两阶段搜索模式,相比于简单穷举搜索(exhaustive search)而言,这两种方案均在一定程度上有效降低搜索复杂度,缓解协议包头负担。然而随着码本数目的增加,这类基于遍历搜索的算法依然会受到搜索维数灾难的影响,其搜索时间将变得难以承受。
本文首次以最大化收-发设备之间的信号传输功率为目标函数,将波束搜索问题建模成2维波束编号平面上的数值化寻优问题。充分利用天线阵元数增多时,所形成的波束越细这一特性,基于分区而治(dividing and conqueing)的思想提出一种逐步细化准则下波束搜索算法。分析表明,相比于现有算法呈现出的O(N)甚至O(N2)搜索复杂度,该算法具有对数搜索复杂度O{ log2(N) },实验仿真进一步验证了本算法的有效性。
2 系统模型及直接搜索算法
2.1 系统模型
使用波束赋形技术的系统发射端含Mt个天线阵元,接收端含Mr个天线阵元,在发射端,信号乘以发送权重矢量w后发射到空间中;相应地,接收端将接收信号乘以接收权重矢量c后,进行加权求和得到输出信号送至信号处理模块[3,10,11]。为降低功耗和实现复杂度,实际60 GHz通信设备中,加权矢量各分量均为相移因子,即|wi|= 1 。因此,可简单地将发射信号经过不同相移后,利用阵列天线发射出去[3,10,11]。
波束码本可定义为一个M×N的矩阵W,其中行数M为天线阵元数,列数N为波束数目,为降低增益损失,一般设置N=2M[3,10,11]。对于均匀分布的1维线性阵,其第n个波束的阵列响应因子为[3]

其中wm,n为码本中第n个波束的第m个天线阵元的加权因子,d为天线阵元间距,λ为信号的波长,θ为来波方向与天线阵法线方向的夹角(波达角),一般设置d=λ/2。
文献[12-16]给出了毫米波通信环境下的信道模型及冲击响应,这里采用IEEE 802.15.3c的信道模型[13]。

其中L是总的路径簇数目(paths),Kl是第l簇路径中的子路径数目(sub-paths),αk,l为相互独立的路径复增益,τk,l为对应的时延,θk,l和φk,l分别为接收端和发送端的信号到达角和离开角,文献[13]给出了其各自的分布律。由此,可以得出接收信号的信噪比为

式中Ap(θ),Aq(φ)分别代表接收端和发射端的波束阵列响应因子,p和q分别为收端和发端所选用的波束编号(即式(1)中的n),θk,l和φk,l分别为第k簇中第l条子路径的发送端和接收端信号波达角,为噪声功率。Δφ表示信号的有效发射窗口,即对于每条路径,只有对应于发射端的Δφ角度范围内的信号将被接收到。这里近似认为对于每一条路径,接收端的阵列响应因子Ap(θk,l)为常数。对于一对分别具有32个天线阵元相距在10 m范围内的天线阵来说,其有效发射窗口Δφ大小约1°到10°左右。考虑到经过波束赋形后发射能量将会非常集中,在设备间存在直射径情况下,为简化分析,可将非直射径的传播能量忽略,此时SNR可简化为

波束搜索的目的为通信双方在各自的波束码本中搜索出最优波束popt,qopt用于通信,即
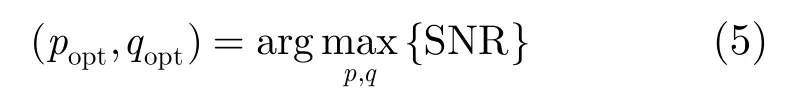
假设噪声功率与来波方向不相关,则此时信噪比仅依赖于接收功率,因而优化目标函数可以简单定义为接收功率。由此,可以得到接收功率与收发波束对对应的离散2维曲面,如图1所示。图1中,x,y坐标分别为发送端和接收端的波束编号,设置收发双方各有32天线阵元,因此各有64个波束,同时设置有效发射窗口Δφ=8°,并将接收到的功率进行了归一化处理。
2.2 现有波束搜索算法

图1 接收功率2维曲面
假设相互通信的两个设备(通信请求端Initiator和响应端Responder)天线阵元数分别为MI,MR,波束总数为NI,NR(NI=2MI,NR=2MR)。对于最基本的遍历搜索而言,通信双方将进行NI×NR次训练序列的发送,方可确定出最优波束对。已有的标准(IEEE 802.15.3c[5], IEEE 802.11ad[6])均在此基础上进行了优化改进,但是由于搜索算法依然基于遍历搜索,因此复杂度(训练序列发送次数)仍然过高。
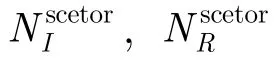

由式(6)可看出,IEEE 802.15.3c中的波束搜索仍然具有平方复杂度。与之类似,IEEE 802.11ad的波束赋形同样分为两个阶段并基于遍历搜索,其复杂度甚至高于N3c,具体可参考文献[6]。
2.3 直接2维曲面搜索
由 2.1节的分析可知,波束搜索问题最终转化为2维曲面的最优化问题,优化的目标函数即为接收到信号的功率强度。但是实际中功率曲面的梯度信息是未知的,因此首先可以想到的是,利用无约束直接搜索(direct search)算法在该曲面上搜索,这无疑会大大降低搜索复杂度。然而,通过对这种直接搜索的方法进行仿真后却发现其搜索成功率很低,如图2所示。在图2中,搜索值为算法的搜索结果,而最大值则为实际的最大功率值。仿真结果显示该方法的成功率只有45%左右。经过分析,其原因是由于有波束旁瓣的存在,使得接收功率曲面存在众多的褶皱(局部最小值,如图1),当使用直接搜索算法的时候,算法经常停留在局部最优值而提前终止,因此造成了搜索成功率较低。
3 逐步细化波束搜索算法

图 2 直接2维搜索仿真结果
由上节知,由于现有标准中的波束赋形的实现算法均为基于遍历搜索,随着天线阵元数目的增多,波束搜索过程的能耗和时耗将大大增加,这极大地限制了波束赋形技术所带来的优势。同时由于旁瓣的存在使得接收功率曲面存在很多褶皱,这也使得直接搜索算法难以工作。为此,本文提出一种逐步细化的搜索方法(Step-Wisely Refinement, SWR),其基本思想是首先使用较宽的波束搜索(这可以使用较少的天线阵元数来产生),然后再使用具有较高方向分辨率的细化波束继续搜索,逐步发现具有不同主瓣宽度波束下的最优波束对。这样,经过若干次迭代搜索之后,将最终确定最优波束对。
3.1 理论分析


其中δ=2π(d/λ) sinθ为加权后相邻阵元所接收信号间的相位差。令|An(θ)|= 0 ,可求出主瓣两侧的第1对零增益点为δ=±2π/M,因而零点主瓣宽度为
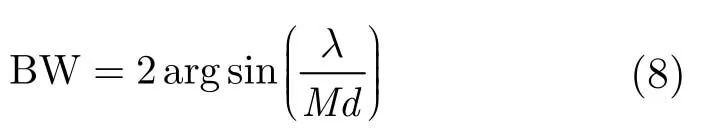
显然,由式(8)可明显看出主瓣宽度将随着天线阵元数目的增多而变窄。

在每一轮细化搜索过程中,算法将在类似图 1所示的功率曲面(搜索空间)上进行 2维搜索。当天线阵元数目加倍时,波束数目也将加倍,因而若上一轮细化搜索的结果 (p(i-1),q(i-1))为全局最优点,则本轮最优波束编号与初始波束编号最多只相差 1。由于波束数目N=2M,相邻波束的主瓣方向弧度差为π/(2M),由式(8)可得

由式(9)可以得出,对于均匀加权直线阵,在每轮细化搜索过程中,初始波束对的主瓣方向必然在本轮最优波束的主瓣范围内。因此在每轮细化搜索过程中,算法均能够终止于全局最优点,同时,算法只需简单地遍历包括初始点以及其周围的8个点(共9个点)即可得出本轮的全局最优点。
3.2 算法描述及复杂度分析


表1 算法描述
对于一对天线阵元数均为M的相互通信的设备,整个搜索过程的迭代次数显然为log2M。假设在首轮 2维搜索过程中平均探测点数为c;而在i> 1 时每轮细化搜索过程中,算法需要遍历9个点,因而本算法的搜索复杂度为
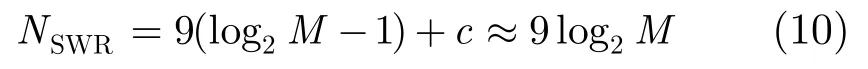
即本算法的渐进复杂度为O{ log2N}(这里使用字母N是为与算法复杂度分析的惯用字母相一致)。这相对于现有标准无疑有极大性能提升。
4 数值模拟
图3为仿真结果,其中图3(a)为搜索复杂度,图3(b)为搜索结果。其中横坐标为仿真实现的序号,图3(a)纵坐标为搜索复杂度,图3(b)纵坐标为功率值。仿真时进行了100次随机实现,设置收发双方的天线阵元数均为 32,因此双方各有 64个波束方向,同时设置有效发射窗口大小为8°,可以看到搜索结果很好地符合了实际全局最优值。可以看出,平均需要大约44个搜索点也即平均大约需要44次收发训练序列即可。

图3 搜索复杂度(a)与搜索结果(b)
图4对本算法的稳健性进行了仿真,比较了随着有效发射窗口的改变,也即设备间距离改变时算法的复杂度以及成功率的变化特性。图中横坐标为有效发射窗口,左侧纵坐标为搜索复杂度,右侧纵坐标为成功率统计。仿真时每改变一次有效发射窗口值,均进行100次随机实现并取其均值。同时将搜索值大于实际最优值95%时统计为搜索成功,即搜索结果比实际最优值损失小于0.22 dB。从图中看出,本算法搜索复杂度稳定在44次以下,并且全部搜索成功,因而本算法对于不同的有效发射窗口(设备距离)保持了稳定工作性能。
图5显示了随着天线阵元数的增长,搜索复杂度的增长情况。其中横坐标为设备的天线阵元数,纵坐标为搜索复杂度。图中对于本文算法的每一点均为进行100次随机实现后得出复杂度均值,而对于IEEE 802.15.3c,则分别给出了sector2,4,8,16N= ,其余的条件相同的情况下的搜索复杂度。从图中可以看出,随着天线阵元数的增加,本文算法的复杂度要明显优于IEEE 802.15.3c的搜索复杂度,而所付出的代价为波束码本的增大。这为60 GHz毫米波通信设备以支持较大天线阵提供了性能保障。
5 结束语
本文对60 GHz通信系统系统提出了一种逐步细化的波束搜索算法,该算法以接收信号的功率作为优化目标函数,并充分利用波束的宽度随天线阵元数的增多而变窄的特性。理论分析和仿真实验均证明了该算法仅具有O{ log2(N) }的搜索复杂度,这相对于已有标准中基于遍历搜索的算法,其搜索性能得以极大的提高。同时可看出,该算法并不需过多的计算量。同时,该算法不仅适用于60 GHz通信系统,其对于任意基于码本的多波束切换系统以及多维天线阵具有普遍的适用性。
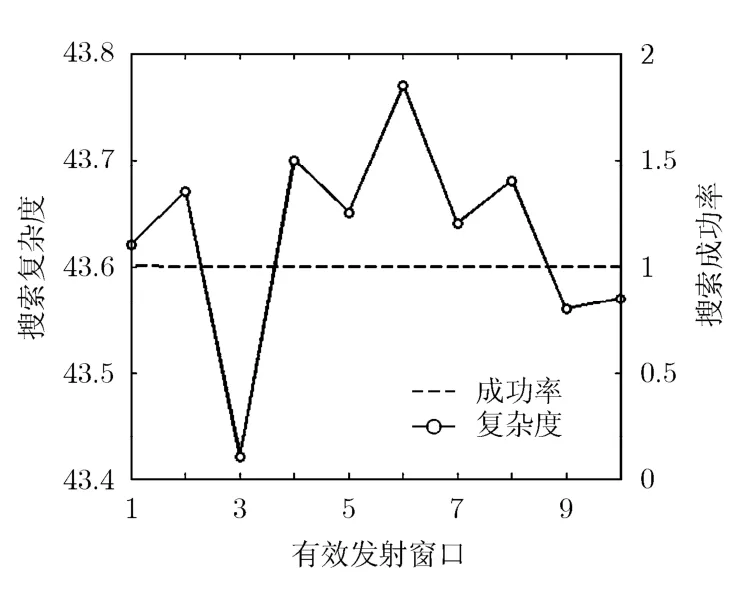
图4 有效发射窗口改变时的算法性能
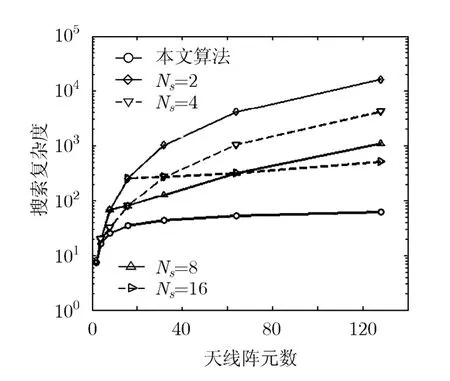
图5 本算法和IEEE 802.15.3c中波束搜索算法复杂度对比
[1]Maruhashi K, Kishimoto S, Ito M,et al.. Wireless uncompressed-HDTV-signal transmission system utilizing compact 60-GHz-band transmitter and receiver[C]. IEEE MTT-S International Microwave Symposium Digest, Long Beach, CA, June 12-17, 2005: 1867-1870.
[2]Xia Peng-fei, Qin Xiang-ping, Niu Hua-ninget al.. Short range gigabit wireless communications systems: potentials,challenges and techniques[C]. IEEE International Conference on Ultra-Wideband, ICUWB, Singapore, Sep. 24-26, 2007:123-128.
[3]Wang J, Lan Z, Pyo C,et al.. Beamforming codebook design and performance evaluation for millimeter-wave WPAN[C].Proc. of the IEEE Vehicular Technology Conference (VTC 2009 Fall), Anchorage, USA, Sep. 20-23, 2009: 1-6.
[4]Tan Y C M. Computational modelling and simulation to design 60 GHz mmwave antenna[C]. 2010 IEEE International Symposium Antennas and Propagation and CNC/USNC/URSI Radio Science Meeting, Toronto, Canada, July 11-17,2010: 1-4.
[5]James P K. Gilb(Technical Editor). IEEE Standards 802.15.3cTM——Part 15.3: Wireless Medium Access Control (MAC)and Physical Layer (PHY) Specifications for High Rate Wireless Personal Area Networks (WPANs) Amendment 2:Millimeter-wave-based Alternative Physical Layer Extension[S]. New York, USA, IEEE Computer Society, 2009.
[6]Cordeiro C(Technical Editor). IEEE P802.11ad TM/D0.1——Part 11: Wireless LAN Medium Access Control(MAC) and Physical Layer (PHY)Specifications-Amendment 6: Enhancements for Very High Throughput in the 60 GHz Band[S]. New York, USA, IEEE 802.11 Committee of the IEEE Computer Society, 2010.
[7]Xu Hong-hua and Liu Ke. Research on wireless communication networks in the 60 GHz frequency band[C].2010 International Conference on Internet Technology and Applications (iTAP), Wuhan, China, Aug. 21-23, 2010: 1-4.
[8]Winters J H. Smart antennas for wireless systems[J].IEEE Personal Communications, 1998, 5(1): 23-27.
[9]Chryssomallis M. Smart antennas[J].IEEE Antennas and Propagation Magazine, 2000, 42(3): 129-136.
[10]Wang Jun-yi, Lan Zhou, PyoChang-Wooet al.. Beam codebook based beamforming protocol for multi-gbps millimeter-wave WPAN systems[J].IEEE Journal on Selected Areas in Communications, 2009, 27(8): 1390-1399.
[11]Wang Jun-yi, Lan Zhou, PyoChang-Wooet al.. Beam codebook based beamforming protocol for multi-gbps millimeter-wave WPAN systems [C]. GLOBECOM 2009-2009 IEEE Global Telecommunications Conference, Honolulu,HI, USA, Nov 30-Dec 04., 2009: 1-6.
[12]Foerster J R, Pendergrass M, and Molisch A F. Channel model for ultra-wideband personal area networks[J].IEEEWireless Communications, 2003, 10(6): 14-21.
[13]Yoon Seokhyun, Jeon Taehyun, and Lee Wooyong. Hybrid beam-forming and beam-switching for OFDM based wireless personal area networks[J].IEEE Journal on Selected Areas in Communications, 2009, 27(8): 1425-1432.
[14]Hirokazu Sawada, Kazuya Fujita, Shuzo Katoet al.. Impulse response model for the cubicle environments at 60 GHz[C].2010 Asia Pacific Microwave Conference-(APMC 2010),Yokohama, Japan, Dec. 7-10, 2010: 2131-2134.
[15]Hirokazu Sawada, Kazuya Fujita, Shuzo Katoet al.. Impulse response model and parameters for indoor channel modeling at 60 GHz[C]. 2010 IEEE Vehicular Technology Conference(VTC 2010-Spring), Taipei, China, May 16-19, 2010: 1-5.
[16]Papio A, Grau A, Balcells Jet al.. 60 GHz channel characterization using a scatterer mapping technique[C].2010 4th European Conference on Antennas and Propagation(EuCAP), Barcelona, Spain, Apr. 12-16, 2010: 1-5.

