基于ARIMA模型的外汇占款预测

崔连翔，曾繁华，黄万华

0 引言

央行为维持汇率稳定而在外汇市场抛本币购外汇的行为，增强了货币供给的内生性，通过外汇占款渠道投放基础货币越来越多，并日益成为基础货币的主要来源。而这将通过货币乘数作用,导致货币供应量更大幅度增加。在其他条件不变的情况下，货币供应量增加意味更多缺乏商品与服务支撑的绝对剩余购买力流入市场，市场供需只有通过物价上涨的方式才能实现新的均衡。

外汇储备增加并非必然地对物价水平产生影响，只有在货币当局为保持汇率稳定而在外汇市场以本币收购外汇时，才会导致因外汇占款的大量被动投放而对物价水平产生较强的通胀压力。外汇储备主要以外汇占款为中介影响物价水平，因此冲销外汇储备对物价上涨的压力，其实际就是冲销外汇占款增长所形成的过量流动性。

本文用Johansen协整检验方法，对外汇储备与物价水平的长期均衡关系进行协整检验，并利用ARIMA模型对外汇占款数据的变化趋势进行短期预测。

1 外汇储备与物价水平的协整检验

1.1 数据的选取、处理与检验

外汇储备以外汇占款为中介，通过货币发行量对物价水平产生影响。因此，本文将对物价水平(CPI)、外汇储备额(FR)及货币供应量（M1）之间的关系进行实证检验。本文外汇储备FR和货币发行量M1的月度数据由中国人民银行网站的统计数据整理计算，CPI数据源自Wind资讯。为减缓数据波动和消除异方差，本文对数据均做对数化处理，并分别用LCPI、LFR、LM1表示，所有检验均由EVIEWS 6.0完成。

经典回归模型建立在稳定变量的基础上，对非稳定变量用经典回归模型进行回归，将会导致“伪回归”。但若非稳定变量之间存在某种线性组合为I(0)，即它们之间是协整的，则可用经典回归模型方法进行回归。本文将用协整检验方法，利用2001年1月至2011年8月的月度数据，对外汇占款与通货膨胀间的长期关系进行检验。

1.1.1 单位根检验

变量间存在协整关系的前提是变量原序列都是非平稳序列，且各序列均为一阶单整序列，即服从I(1)。因此进行协整检验之前，首先应对各序列进行单位根检验，为了减缓数据的剧烈波动，对各组数据均做对数化处理。

表1 原序列单位根检验

从表1检验结果可知，原序列的ADF值均大于显著性10%的临界值，因此，不能拒绝有一个单位根的原假设，认为原序列均存在单位根，即原序列均是非平稳的。

表2 一阶差分序列单位根检验

从表2检验结果可知，一阶差分后序列的ADF检验值均小于显著性1%的临界值，且含有一个单位根的概率P值均小于1%，因此可以拒绝差分后序列有一个单位根的原假设，接受一阶差分序列不存在单位根的备选假设，一阶差分后序列是平稳的。

ADF检验结果表明，LCPI、LFR和LM1均为一阶单整序列I(1)，满足对其进行协整检验的条件。

1.1.2 Granger因果检验

为防止序列间出现伪相关，在进行协整检验前，对序列进行Granger因果检验，其滞后2阶的检验结果如下：

表3 Grnager检验

从表3检验结果看，LFR是LCPI的格兰杰成因，即外汇储备与物价水平间存在显著地因果关系，外汇储备变动会引起物价水平的变化；LCPI与LM1互为格兰杰原因，即一方面物价水平的变动会引起货币发行量的变化，另一方面货币发行量的变动也会影响物价的变化。LFR与LM1互相都不是对方格兰杰原因，这可能是因为中央银行采取的货币冲销操作有效缓解了外汇占款投放导致的货币扩张压力。

经检验，可以确认序列LCPI与LFR、LM1之间存在因果关系，序列间不存在伪相关，序列间的关系具有现实经济意义。

1.2 Johansen协整检验及标准化协整方程

1.2.1 最优滞后期

协整检验对滞后期的选择极为敏感，故在进行协整检验前应先确定滞后期。因为协整检验进行回归的是原序列的差分序列，所以协整检验中的滞后期比无约束VAR模型最优滞后期少一期。即若无约束VAR模型的最优滞后期为p，则协整检验方程所设定的的滞后期为p-1。

原序列最优滞后期可在无约束VAR模型估计结果窗口进行，并根据LR、FPE、AIC、SC和HQ等标准选出无约束VAR模型的最优滞后期。建立LCPI、LFR和LM1三变量的VAR模型，在EVIEWS估计结果输出窗口，依次选择View/Lag Structure/Lag Length Criteria，并在出现的对话框中输入所要考察的最大滞后期（本文输入EVIEWS自动推荐的8），所得结果如表4所示。

表4 滞后期判别

表4检验结果表明：按照LR、FPE、AIC准则选取的滞后期均为2，而依SC、HQ标准选定滞后期为1。依据多数原则，本文所取滞后期为2，由于协整检验的滞后期比原序列的滞后期少1，可知协整方程的最大滞后期为1。

1.2.2 协整检验

Johansen协整检验通过迹统计量（Trace）和最大特征值（Max-Eigenvalue）统计量进行判定，两者均采用循环检验规则。

（1）迹检验和最大特征值检验

对变量进行滞后1期、序列与协整方程均不含趋势项与截距项的Johansen协整检验，检验结果如表5所示。

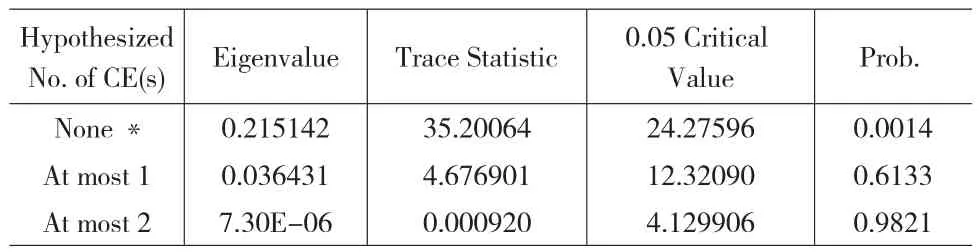
表5 迹检验

在表5检验结果中，原假设None表示至多存在0个协整关系，即没有协整关系，该假设下迹统计量的概率P值为0.0014，表示可以拒绝原假设，认为至少存在一个协整关系；At most 1的原假设为最多存在一个协整关系，该假设下迹统计量的概率P值为0.6133，表示不能拒绝原假设；检验到此结束。通过迹统计量可判断LCPI、LFE和LM1间存在一个协整关系。

表6 最大特征值检验

表6最大特征值的检验规则与迹检验相同，就本文而言，最大特征值的检验结果与迹检验结果一致，认为LCPI、LFR和LM1之间存在一个协整关系。

（2）协整方程

依据Eviews提供的标准化协整关系可得出最终协整方程：从系数t值可知，协整方程的系数均十分显著，检验所得系数符号与理论相符，各序列在5%的显著性水平上存在协整关系。

1.2.3 协整方程解读

从协整方程可得出如下结论：

（1）尽管LCPI、LFR和LM1本身均为一阶单整的非平稳序列，但在样本期内，LCPI、LFR和LM1存在着长期稳定的正相关关系。

（2）在长期内，外汇储备与货币量对物价水平起到明显的推动作用。由于对数函数是常弹性函数，故协整方程的经济意义是：在其它条件不变的条件下，外汇储备每增长一个百分点，将推动物价水平上涨0.57个百分点；而货币量每增加一个百分点，将推动物价上涨0.67个百分点。

2 ARIMA模型的外汇占款预测

虽然从根本上解决外汇储备增长对物价水平形压力问题，需要切断或有效消弱外汇储备与货币发行量间的联系，但在该问题是到根本解决之前，对外汇占款进行被动冲销以减缓过量流动性对物价水平的上涨压力，仍是我国货币当局的重要任务。

对外汇占款进行较为准确的预测，不仅有利于货币当局进行冲销的主动性，而且对货币当局合理组合冲销工具及政策制定都大有裨益。因此，本文将利用ARIMA模型对外汇占款的趋势进行短期预测，以便为需要者提供参考。

2.1 ARIMA模型简述

ARIMA（p,d,q）模型全称是单整自回归移动平均模型，是一种精度较高的时间序列短期预测方法，该模型由Box和Jenkins于上世纪70年代初创立，所以又称为Box-Jenkins模型。任何时间序列都具有ARIMA（p,d,q）的模型形式，该模型包含3种情况，即自回归AR(p)模型、移动平均MA(q)模型和自回归移动平均ARMA(p，q)模型。

2.1.1 ARIMA模型的形式

若时间序列Yt经d次差分成为平稳序列,而该序列的d-1次差分却并不平稳，则称序列为d阶单整序列，记为Yt～I(d)。令 yt=ΔdYt=(1-B)dYt，则 yt是平稳序列，即yt～I(0)，可以对 yt建立ARMA(p,q)模型：

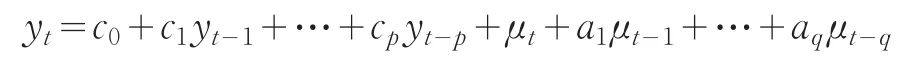
将上式移项，并用滞后算子表示为：

经过d阶差分变换后的ARMA(p，q)模型称为ARIMA（p,d,q）模型，令

Ψ(B)=1-c1B-c2B2-…-cpBp

Φ(B)=1+a1B+a2B2+…+aqBq，

并将yt=ΔdYt=(1-B)dYt代入，则上式可转化为：

Ψ(B)(1-B)dYt=c0+Φ(B)μt

由定义可知，AR(p)和MA（q）分别为ARMA(p,d,0)和ARMA(0,d,q)时的特殊形式。

2.1.2 ARIMA建模过程

对时间序列运用Box-Jenkins方法进行建模时，主要通过序列平稳性检验及运用序列相关图对序列所适合的模型类型进行识别，以确定建模所需的适当的d、p和q。该建模过程主要有以下四个步骤组成：

（1）对原序列进行平稳性检验，并据此确定模型中单整阶数d。

（2）根据序列自相关系数和偏自相关系数，并依简约原则识别p和q的值。

（3）估计模型的未知参数，检验参数的显著性及模型本身的合理性。

（4）进行诊断分析，验证模型预测值与实际值特征的吻合性。

2.2 外汇占款月度数据的ARIMA(p,d,q)建模

本文将依据2000年1月至2011年8月间外汇占款的月度数据进行建模，为了检验模型的预测有效性，将2011年1月至8月的数据留为检验预测效果的备用数据。为了减少数据波动和消除异方差，本文对外汇占款的月度数据进行对数化处理并以LFE表示。

2.2.1 单整阶数d的识别

确定单整阶数d即检验时间序列经过d次差分后才转变为平稳序列，可以通过序列图进行简单和直观的判断：

图1 LFE与DLFE趋势图

从图1中可知，LFE有明显随时间增长而上扬的趋势，具有非稳定序列的特征，经一阶差分后DLFE的时间趋势已经消除，序列值围绕均值（近似为零）上下波动，具有稳定序列的特征。

序列图提供了序列稳定性的直观初步判断，为更精确的识别单整阶数，对LFE和DLFE进行ADF检验，以判别其统计意义上的稳定性，进而确定单整阶数d，用EVIEWS对两个序列分别进行不含截距项和趋势项的单位根检验，检验结果如表7所示。

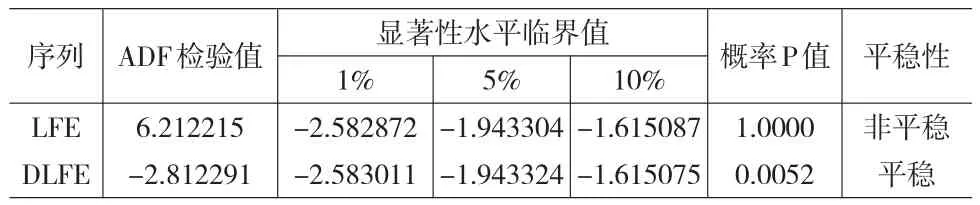
表7 ADF单位根检验

从表7可知，LFE的ADF值6.212215远大于10%显著水平临界值-1.615168，不能拒绝序列具有单位根的原假设，该序列为非平稳序列。而经过为一阶单整序列，其ADF检验值小于1%显著水平下的临界值，可以拒绝DLFE序列具有单位根的原假设，认为该序列为稳定序列。

可知，在经过一阶差分后LFE序列转变为平稳序列，LFE为一阶单整序列，即LFE～I(1)，故可知d=1。

2.2.2 p和q的识别

通过单位根检验可知，时间序列LFE为一阶单整序列。因此，可以借助DLFE，即LFE一阶差分序列的自相关系数ACF图和偏自相关系数PACF图对p和q进行初步判断。若将ACF图和PACF图中相关系数突然降为零称为“截尾”，相关系数逐渐衰减称为“拖尾”，则据此总结出ARIMA模型的图形识别方法如表8所示。

表8 ARIMA模型图形初步识别方法

除利用相关图对ARMA模型进行初步判断外，实际操作中还需用其他辅助准则进行判断。第一，通过试设模型后对其进行比较，选择AIC和SC值最小、调整R 值最大的模型，该方法在判别ARMA(p,q)时最为重要；第二，如果上述判别值无法同时实现，则依“简约原则”进行选择，即选择模型设立单一、滞后期较小的模型；第三，对于AR(p)模型需进行稳定性检验，排除残差存在序列相关性的模型。

对ARIMA(p,d,q)模型中的p和q进行初步识别，首先需利用EVIEWS软件获得D(LFE)序列的相关图，其滞后24期的相关图如下：

图2 DLFE相关图

图中，中心实线表示零轴，此线右边观测值为正值，左边为负值，虚线表示到零轴正负各2倍标准误的置信区间，若相关系数的绝对值超置信区间，则被认为显著不为零。从图中可知，DLFE序列的自相关系数ACF缓慢衰减，具有明显的“拖尾”特征，偏自相关系数PACF在2阶后其值均显著为零，具有明显的“截尾”特征，依据ARIMA模型的图形识别方法，可以初步判定p=2，q=0。因此，可初步判断模型形式为AR(2)，即对LFE序列可建立ARIMA（2，1，0）模型，其模型形式为：

DLFEt=c0+c1×DLFEt-1+c2×DLFEt-2+μt

2.2.3 ARIMA模型估计

从EVIEWS主菜单中选择Quick/EstimateEquation，在弹出的窗口中输入：DLFE C AR(1)AR(2)，或在命令窗口输入：LSDLFECAR(1)AR(2)，得到ARIMA（2,1,0）的输出结果：

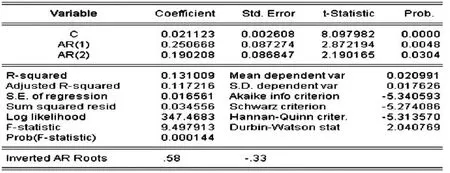
图3 ARMA估计结果

依检验结果可得ARIMA（2,1,0）模型估计方程：

2.2.4 模型的论断与检验

完成模型的识别与参数估计后，还需对估计结果进行检验，以诊断所建立的模型是否合理与可靠。合理的ARIMA(p,d,q)模型须通过三方面的检验：（1）模型参数估计值必须通过显著性水平的t检验；（2）ARIMA(p,d,q)模型的全部特征根的倒数都必须在单位圆内，保证模型的稳定性；（3）模型的残差必须通过Q统计量检验，即残差序列为白噪声序列，不存在自相关。

从模型检验结果可知，模型中各参数的t值均在5%的显著性水平上通过了显著性检验，同时AIC和SC值较小，说明模型的整体效果良好。ARMA模型的输出结果在最后一行提供了AR、MA特征多项式根的倒数，自回归特征方程两个根倒数分别为0.58和-0.33，均在单位圆内，说明模型具有稳定性。

在检验过模型参数显著性和模型稳定性之后，还要利用Q统计量对模型的残差进行白噪声检验，若残差序列不是白噪声序列,意味着残差序列还存在着有用信息没有被提取,需要进一步修正模型。若残差序列是白噪声序列，则意味着所建立的模型是适合的。本文残差序列的样本数量为129个，故该序列检验的最大滞后期取检验结果如图4所示。

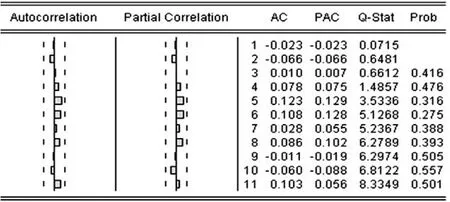
图4 残差相关图

从图4可知，自相关和偏自相关值均在置信区间内，说明残差项估计自相关系数和偏自相关系数值在0.05的显著性水平上与零没有显著差异，Q(11)=8.3349且各期Q统计量的p值都远大于0.05，不能拒绝原假设，认为模型误差序列为白噪声序列，不存在自相关。

以上检验结果表明，ARMA(2,1,0)模型通过了对其进行的各项检验，该模型是合适的。

2.3 ARIMA模型预测

建模的主要目的就是进行预测，为制定货币政策及工具操作提供依据，所以模型的预测性能尤为重要。在用该模型进行预测之前,有必要对其预测能力进行检验。模型预测能力一般用MAPE(平均绝对百分比误差)度量,其计算公式如下:

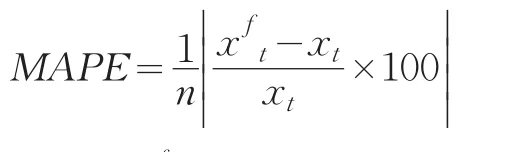
式中，xft为预测值,xt是序列实际值,n是预测期数。MAPE评估预测能力如下:MAPE小于或者等于0.10则表明模型预测能力极佳；0.10～0.20表明预测能力优良；0.20～0.50表明模型预测合理；MAPE大于0.50表明模型预测不正确。

2.3.1 区间内预测

模型预测分为静态预测和动态预测，本文使用静态预测方法进行预测。对模型预测能力的检验分为两部分:对样本期内模型的预测能力检验与对样本期外模型的预测能力检验。

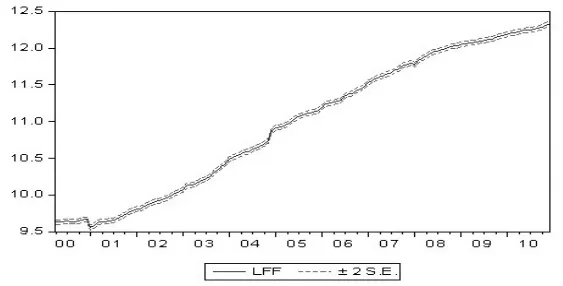
图5 样本期内的预测结果

首先，对样本期间内的数据进行预测，其预测结果如图5。

图5中，中间蓝色实线为LFE的预测序列线图，两则红色虚线为2倍标准误置信区间。从预测结果看，样本期间内，模型的预测值与实际值的平均绝对百分比误差MAPE为0.091141,表明模型在样本区间内的预测能力“极佳”。

2.3.2 区间外预测

为检验模型对样本期外的预测能力，将模型预测区间外推至2011年8月，并将2011年1月至8月的预测值与实际值进行比较。由于静态预测只能进行点预测，即一次只能预测一期，本文通过将预测值逐期加入样本并重新进行预测的方式，来得出各期预测值，结果如表9所示。

表9 静态预测值与实际值

为了更直观的观察其预测效果，作预测值与实际值的序列图：

图6 预测值与实际值

图6中，LFER为实际值序列，LFEF为预测值序列。从表9和图6可知，模型预测误差随预测期延长而扩大，但在8期预测中预测误差均未超0.5%，说明利用该模型进行短期预测效果较好。

预测结果表明，无论样本期内还是样本期外，模型的预测效果都较好，依据模型进行的预测是可靠的。将模型期间外推,利用2000年1月至2011年8月的数据对2011年9月至2012年4月进行预测。为便于对外汇占款数据进行直观分析，在EVIEWS命令窗口中输入GENR FE=EXP(LFE)命令，将预测数据转换为外汇占款的水平值，预测结果如表10所示。

表10 预测值

为直观分析外汇占款的增长趋势，将2009年1月后的实际值及2011年9月至2012年4月的预测值在一个序列图中进行观察。

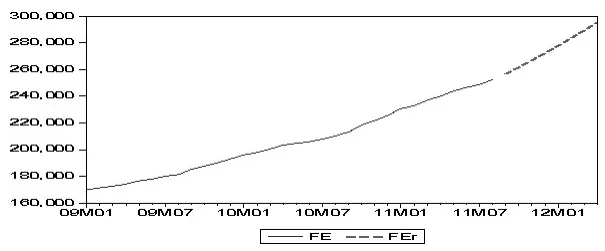
图7 预测值与实际值序列图

图7中FE为外汇占款实际值，FEr为预测值。从预测结果看，外汇占款增长趋势在短期内仍将持续，货币当局进行外汇占款冲销的任务依旧繁重。

3 结论

协整检验结果显示：在长期内，外汇储备与物价水平存在显著正相关，外汇储备持续增长将导致我国物价水平大幅上涨。ARIMA模型检验结果表明：本文建立的模型设立恰当、拟合良好、可信度高。依据ARIMA模型对外汇占款进行较为准确的预测，可增强货币当局进行冲销的主动性和有效性，并为货币政策制定及冲销工具组合选择提供可靠借鉴。

从预测结果可知,我国外汇占款在短期内仍将保持增长态势，通货膨胀压力依旧存在。外汇占款日益成为货币供给的新的主要渠道，对我国货币政策的独立性及有效性的负面影响日益严重。

只有切断外汇增加与货币供应增长的直接联系，才能从根本上解决外汇储备与外汇占款的被动增长，保持货币政策的独立性和有效性，可行方法之一是建立外汇平准基金，并加强对国际热钱进出的监管。除此之外，还需进一步完善外汇管理制度、改善汇率的形成机制以增强汇率弹性、促进外汇市场发展和允许国民自由使用外汇等。这不仅将有效消除外汇储备对我国物价水平的压力，而且可使货币当局从被动冲销的泥潭中解脱出来，专一于其币值稳定的目标并强化其货币政策独立性和有效性。

[1] 邓小勇,杨志明.我国外汇占款变动的预测研究[J].金融发展研究，2011,(5).

[2] 高铁梅.计量经济分析方法与建模[M].北京：清华大学出版社，2011.

[3] 康璐璐.GARCH模型在主要消费指数实证研究中的应用[J].现代商业，2010,(20).

[4] 李海明.外汇储备变动对我国货币政策的影响分析[D].上海外国语大学，2010.

[5] 李海海,曹阳.外汇占款的通货膨胀效应[J].中央财经大学学报，2006,(11).

[6] 易丹辉.时间序列分析方法与应用[M].北京：中国人民大学出版社，2011.

[7] 易丹辉.数据分析与EVIEWS应用[M].北京：中国人民大学出版社，2008.

[8] 张鹏,柳欣.我国外汇储备对通货膨胀的影响[J].世界经济研究，2009,(2).