基于BP神经网络优化算法的工业企业经济效益评估

蔡 云,张靖妤

0 引言

BP神经网络是神经网络中最精华、最完美的一种，企业的经济效益评价问题，从本质上讲属于一类模式识别问题，而人脑在这类问题的处理上有很大的优势，BP神经网络在该领域有着显著的优越性。基于现有评价方法的局限性，本文提出一种基于BP神经网络优化算法的工业企业经济效益评估方法，该方法把传统的因子分析法和BP神经网络算法结合起来，把神经网络的智能化和因子分析的简化结合起来，能避免人为计取权值和相关系数过程中的主观影响和不确定性，优化算法后的BP模型可以大大节约运算时间，很好地实现了快速全面客观进行工业企业经济效益评估。

1 BP神经网络优化算法

1.1 BP神经网络

人工神经网络(Artificial Neural Network)由于其具有大规模并行处理、容错性、自组织、自适应能力以及联想功能强等特点，已成为解决很多实际问题的有力工具。

一个多层人工神经网络模型可以描述如下：

（1）网络包含一个输入层，N(N＞1)个隐含层和一个输出层。

（2）第k层包含Nk个神经元。

（3）第k-1层第i个神经元到第k层第j个神经元的权值表为

BP网络是一种多层前馈型神经网络，其神经元的传递函数是S型函数，输出量为0～1之间的连续量，它可以实现从输入到输出的任意非线性映射。BP学习算法要求神经元模型的传递函数为有界连续可微函数，由具有这种传递函数的神经元组成的网络，通过学习可以用一个连续的超曲面（而不仅仅是一个超平面）来完成划分输入样本空间的功能。在输入样本空间复杂的情况下，采用输入层、隐含层、输出层三个层次，各层间实现全连接，此时学习后的网络可以以n-1个超曲面构成一个符合曲面，完成复杂的分类任务，弥补了单层感知器的缺陷。BP神经网络结构通过误差反向传播来消除误差。在训练中通过计算输出值与期望值之间的误差，来求解输出层单元的一般化误差，再将误差进行反向传播，求出隐含层单元的一般化误差，调整输出层和隐含层及输入层之间的连接权值与隐含层、输出层的阈值，直到系统误差可以接受为止，此时的权值、阈值不再改变。其中三层前馈BP神经网络的结构如图1所示。

X=(x1，x2，……，xn)T为输入向量，Y=(y1，y2，……，ym)T为输出向量，n表示输入向量的维数，m表示输出向量的维数。各层间神经元形成全互联接，各层次内的神经元没有任何耦合。

虽然BP算法在神经网络中得到了广泛的应用[3]，但由于BP算法是一种误差逆向传播的算法，该算法不具有全局搜索能力，导致该算法训练次数多使得学习效率低，收敛速度慢。

1.2 BP神经网络改进算法

本文采用了动量法和学习率自适应调整的策略，从而提高了学习速度并增加了算法的可靠性。动量法降低了网络对于误差曲面局部极值的敏感性，有效地抑制了网络陷于局部极小。标准BP算法实质是一种简单的最速下降静态寻优算法[4]，在修正权值或权值向量X(k)时，只是按照时刻的负梯度方式进行修正，而没有考虑到以前积累的经验，即以前时刻的梯度方向，从而常常使学习过程发生振荡，收敛缓慢。改进的算法为:

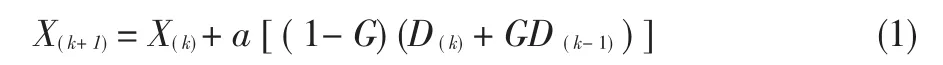
其中:X(k)既可表示单个的权值，也可表示权值向量，D(k)=-5E/5X(K)为k时刻的负梯度，D(k-1)为k-1时刻的负梯度，a为学习率(a＞0)，G为动量因子，G∈[0，1]。

这种方法所加入的动量项实质上相当于阻尼项，它减小了学习过程的振荡趋势，从而改善了收敛性。自适应调整学习率有利于缩短学习时间。标准BP算法收敛速度慢的一个重要原因是学习率选择不当，学习率选得太小，收敛太慢;反之，则有可能修正过速，导致振荡甚至发散。自适应调整学习率的改进算法可表示为:

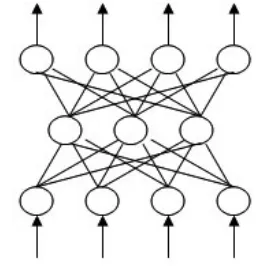
图1 前馈神经网络模型

2 运用优化BP神经网络算法进行工业企业经济效益评估

2.1 BP模型的建立

建立一个神经网络模型并完成训练学习，主要包括三个阶段:配置阶段、训练阶段、分类阶段。

第一，输入节点的选择。工业企业经济效益的评估可根据一系列的主要经济技术指标来度量。本文是将《2010中国工业经济统计年鉴》中部分省、市、自治区独立核算的27个城市的工业企业的9个监测指标值作为BP模型的输入节点。评估指标临界点的确定，一方面是参照国际上公认的标准，另一方面充分结合了中国的实际情况。这9个工业企业经济效益评价的指标为：x1：100元固定资产原值实现产值（%）；x2：100元固定资产原值实现利税（%）；x3：100元资金实现利税（%）；x4：100元工业总产值实现利税（%）；x5：100元销售收入实现利税（%）；x6：每吨标准煤实现工业产值（元）；x7：每千瓦时电力实现工业产值（元）；x8：全员劳动生产率（元/人.年）；x9：100元流动资金实现产值（元）。进行输入节点的输入时，需要对原始数据进行归一化处理，将它们转化为闭区间[0，1]上的无量纲性指标值，本文采取的归一化方法是将每一指标值除以各自领域上的最大值。

第二，隐层节点数的选择。隐单元数的选择与输入输出单元的多少有直接的关系，可参考以下公式确定:n1=（m+n）/2+a。其中m为输入神经元数，n为输出神经元数，a为1-10间的常数，本文取n1=10。

第三，输出节点的选择。输出节点的选择对应于评价结果。为此，需要确定期望输出。在神经网络的学习训练阶段，“样本”的期望输出值应该是已知量，它可由历史数据资料给定或通过一些数学统计方法评估得出。本文采用多变量因子分析法的评价结果作为期望值。

首先，根据《2010中国工业经济统计年鉴》中28个省、市、自治区独立核算工业企业的9个经济指标的原始数据，利用主成份法提取出4个公因子[5][6]，其累计方差达到96.244%(96%以上)，这4个公因子是相互独立的，分别代表企业经济效益的4个方面，集中反映了我国省、市、自治区独立核算的工业企业的经济效益状况，因此分析具有很大的客观性。4个公因子的表达式为：

F1=0.358x1+0.391x2+0.404x3+0.449x4+0.413x5+0.415x6+0.107x7+0.082x8-0.037x9

F2=-0.438x1+0.347x2+0.328x3+0.052x4-0.227x5-0.272x6+0.672x7+0.413x8-0.154x9

F3=0.050x1-0.391x2-0.316x3-0.224x4+0.406x5+0.298x6+0.664x7+0.391x8+0.241x9

F4=0.807x1-0.057x2+0.007x3-0.012x4-0.407x5-0.306x6+0.292x7-0.372x8-0.476x9

其次，计算出各地区工业企业公因子得分如表1所示，以各公因子的方差贡献率占4个因子总方差贡献率的比重作为权重进行加权汇总，得出各工业企业经济效益的得分F(F=(62.700×F1+14.813×F2+13.493×F3+5.238×F4)/96.244)，其因子得分见表1。

将工业企业经济效益状况分为I[1000]很差，Ⅱ[0100]较差，Ⅲ[0010]较好，Ⅳ[0001]很好4种不同的效益好坏程度，分别对应于因子得分表中的4种状态:F∈(-1，-0.70)，F∈（-0.70，0），F∈（0，0.8），F∈（0.8，2）。

表1 各城市因子得分表

表2 27城市神经元值

表3 各城市工业企业分类经济效益评价

2.2 BP优化算法模型的训练与检测

运用改进的BP神经网络模型对工业企业经济效益的模型进行学习训练，把隐层的阈值函数由sigmoid函数变为gauss函数，输出层根据样本自适应的sigmoid函数，误差标准采用标准均方误差。如前所述，本文建立的BP模型共有9个输入神经元，10个隐层神经元，4个输出神经元；实验中学习率η=0.1，动量系数α=0.6，可接受的误差标准ε=0.001。我们利用前1～27个省、市、自治区独立核算工业企业的衡量企业经济效益状况的27个模式对这一神经网络进行学习训练175次后达到误差要求。在完成神经网络的训练后，用第28个城市即新疆自治区独立核算工业企业的经济效益样本值对模型进行检验。

2.2.1 模型的训练

训练时，27个城市独立核算工业企业的9个输入神经元的值如表2所示（其中xi，i=1～9表示效益评价指标，每行代表1个城市工业企业的各个经济指标值）。

各个城市工业企业的期望输出、模型的实际输出以及由它们分类得到的经济效益评估如表4-表5所示：

2.2.2 模型的检验

表4 第28个城市新疆自治区的指标输入

表5 模型实际输出

通过优化算法BP模型检测运算表明：

（1）优化算法后的模型通过175次后达到误差要求，仅为标准BP模型运算次数的20%左右，大大缩短模型的评价运行时间。

（2）实际输出与期望输出非常接近，误差ε=0.001也满足要求。同时我们知道上述评估和分析结果与我国各省、市、自治区独立核算工业企业实际情况是完全一致的：上海、江苏、浙江、北京、天津，这五个省、市、自治区的经济效益在全国来说是很好的，其中上海的经济效益最好。而青海、宁夏、山西、内蒙的经济效益是很差的。

因此，优化算法后的BP模型可大大节约运行时间并具有很好的评估分析效果，可用此神经网络模型对我国省、市、自治区独立核算的工业企业进行经济效益的评估和分析。

3 结语

本文在现行工业企业效益评价方法的基础上提出了更客观的评估方法，应用BP神经网络进行工业企业经济效益评估的可行性。将企业的经济指标作为人工神经网络的输入，结合提出的优化算法模型，利用网络的分类功能对企业进行分类评估，算例表明了该方法的可行性。但随着社会发展，传统的工业企业经济效益评估方法将不能全面反映企业情况，更客观、更多元化的评估方法将被尝试提出。因此，本文提出的方法将在工业企业经济效益评估领域或类似领域中发挥积极的作用。

[1] 史林渠.基于层次分析法与模糊综合评价的绩效考核研究[J].北京石油管理干部学院学报,2011,(3).

[2] 钱芝网.BP神经网络及其在供应商选择评价中的应用[J].工业工程与管理,2011,(3).

[3] 齐振国，楚建东.基于BP神经网络的项目评估模型研究[J].沈阳师范大学学报(自然科学版),2010,(1)．

[4] 赵川，杨洁，曾强，刘爱军.遗传算法改进的BP神经网络在协同创新评价中的应用[J].机械,2010,(8).