竞争供应链在突发事件下的决策及协调策略
侯 玲,陈东彦,滕春贤
0 引言
近来年,经济全球化环境中的市场竞争越来越体现在供应链之间的竞争,正如全球领先的企业管理软件公司甲骨文公司总裁拉里·埃里森所说:市场上只有供应链而没有单个的企业,21世纪的竞争不再是企业与企业之间的竞争,而是供应链与供应链之间的竞争。因此,给出供应链竞争环境下供应链的决策具有重要的理论意义和实际价值。本文将把扰动引进到竞争供应链的协调管理研究中,并给出扰动下竞争供应链的协调策略。
1 基本模型与假设
1.1 模型假设
如图1所示,假设在市场中有两条竞争的供应链,每条供应链由一个制造商和一个零售商组成,销售具有质量差异的可替代产品,且两条供应链间信息完全对称。假设制造商i(i=1,2后同)的单位产品生产成本为ci,单位批发价格为ωi;零售商i的单位产品零售价格为 pi(给定的外生变量),单位缺货损失为bi,未售出的产品的商誉损失vi,且 pi>ωi>ci>vi。假设两种产品的随机总市场需求量为d,其分布函数和概率密度函数分别为Fp(x)和fp(x)。其中 p=(p1,p2)表示两种产品的价格向量,即产品的总需求受价格的影响,且设Fp(x)为严格单调增加的二次可微函数,满足Fp(0)=0,Fp(∞)=1,其反函数为,显然仍为严格单调增加的二次可微函数。
不难看出,在上述假设下若想探讨两条竞争供应链的决策,必须首先给出每种产品的需求情况,下面对此进行分析。
由于两种产品为不同质产品,消费者的选择受自身工资水平、产品价格及品牌效应等的影响,因此假设消费者对产品i的需求受产品价格 pi和顾客服务水平Si的影响。并假设消费者对产品特征Si的偏好系数为a,则消费者对产品i的效用函数可描述为
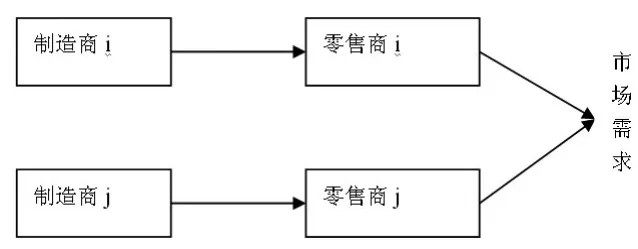
图1 竞争供应链系统结构图

其中,U0为两种产品的固定效用。显然,产品价格越低,则服务水平越低,即当 p1<p2时,有S1<S2。因此,两种产品的效用函数可用图1表示。
其中,a0∈(0,+∞)。在市场中由于不同的消费者有不同的偏好系数,设消费者对产品服务水平的偏好a服从连续随机分布,分布函数和概率密度分别为H(a)和h(a)。由图1知,a0是两种产品的效用函数的交点,即满足下式

图1 产品1和2的效用函数图
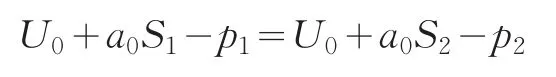
那么
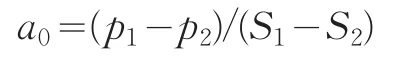
一般的,消费者将选择两种产品中效用较大的产品,因此可分别得出市场上两种产品的市场份额
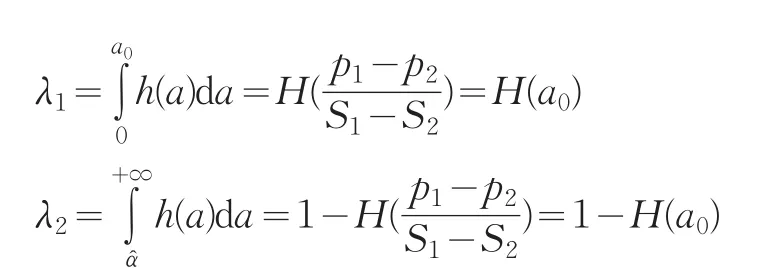
不难看出,增大产品i的服务水平Si,则产品i的市场份额会增大,即dλi/dSi>0;增大竞争对手产品 j的服务水平Sj,产品i的市场份额会减小,即dλi/dSi<0;增大产品i的价格 pi,则产品i的市场份额会减小,即dλi/dpi<0;增大竞争对手产品 j的价格 pj,产品i的市场份额会增大,即dλi/dpi>0。
由于当产品偏好a0固定时,两种产品的市场份额将固定,现假设两种产品的市场份额分别为λi和 λj,且λi+λj=1,则两种产品i、j的需求函数可分别表示为
di=λiD,dj=λjD
因此,产品i的需求di的分布函数和概率密度函数分别为

综上,在实际的市场中,在给定市场总需求的情况下,我们可以根据每种产品的价格和消费者对产品的偏好来获得供应链竞争环境下各单链的市场需求情况,因此在供应链的运作过程中各参与者可通过调节影响产品的特征函数来提高自身在市场中的竞争优势。
1.2 基本模型
在上述假设下,产品i的期望销售量为
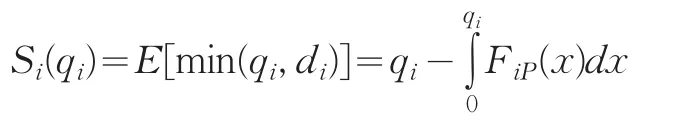
期望未销售量为
Li(qi)=qi-Si(qi)
经推导,可得零售商i、制造商i和供应链i的期望利润分别为

2 基准决策模型
如果供应链内部存在盟主成员,以最大化整条供应链的利润为目标进行决策,称此类供应链为集权式供应链。如果供应链成员以最大化自身利润为目标进行决策,则称此类供应链为分权式供应链。所谓协调供应链的实质是建立相应的机制使分权供应链利润与集权供应链利润相一致。
2.1 两供应链的集权式决策
当两供应链均采用集权式决策时,供应链i的最优决策为:

由于Πi(qi)是关于qi的可微凹函数,即所以Πi(qi)关于qi的一阶必要条件是求解优化问题(7)的充要条件,通过求解可得到此时供应链i的最优订货量为

不难看出,最优订购量随自身供应链所获得的市场份额增大而增大,随竞争供应链的市场份额增大而减小。
2.2 分权式决策下的协调契约设计
在2.1节中,仅给出了两竞争供应链均集权决策时的最优决策,但在实际的市场运作中,供应链一般表现为分权形式,而分权供应链很难达到集权供应链的效果,因此研究竞争供应链的契约形式非常重要。假设制造商i采用回购加线性补贴加利润共享契约(ωi,ei,zi,ϕi),即在此契约下,零售商i按单位批发价格ωi向供应商i订购货物,供应商i对过剩产品或不足产品按(ei,zi)给零售商补贴成本,零售商i在销售季节结束后需要把一定比例的销售收入支付给制造商i。其中,ei为回购价格,zi为线性补贴价格。假设支付比例为1-ϕi,有如下定理:
定理1在供应链竞争环境下,若制造商i采用回购加线性补贴加利润共享契约,则无论制造商 j采用何种契约形式,只要(ωi,ei,zi,ϕi)满足关系式
ωi=ϕici+(1-ϕi)pi,ei=(1-ϕi)(pi-vi),zi=(1-ϕi)bi
则回购加线性补贴加利润共享契约可使分权供应链利润与集权供应链利润相一致。
由此可见,如果制造商i采用回购加线性补贴加利润共享契约,则无论竞争供应链采用何种契约,只要制定合适的契约参数,都可增加供应链系统整体利润,实现供应链成员的共赢。
推论1在供应链竞争环境下,若两个制造商均采用回购加线性补贴加利润共享契约,则当ωi=ϕici+(1-ϕi)pi,ei=(1-ϕi)(pi-vi),zi=(1-ϕi)bi(i=1,2)时,两分权供应链可同时达到集权供应链的效果。
3 需求和成本发生扰动后竞争供应链的最优决策及协调策略
在实际的市场运作中,由于突发事件的存在使得需求和成本发生变化,例如“911”袭击事件导致航空需求的突然下降,禽流感的爆发使得对家禽的需求大幅度下降等等。而不可预测的需求的变化,又导致制造商的生产成本发生变化。那么在需求和成本均发生扰动的情况下,竞争供应链应如何决策,扰动后的竞争供应链如何达到完美协调,这也是亟待解决的问题。
3.1 扰动发生后集权供应链的决策
扰动下供应链i的期望销售量、期望未销售量变为

而整条供应链i的利润变为


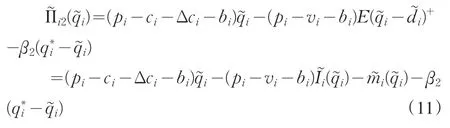
定理2在供应链竞争环境下,当突发事件导致市场随机需求和生产成本同时扰动时,供应链i的最优订购量为
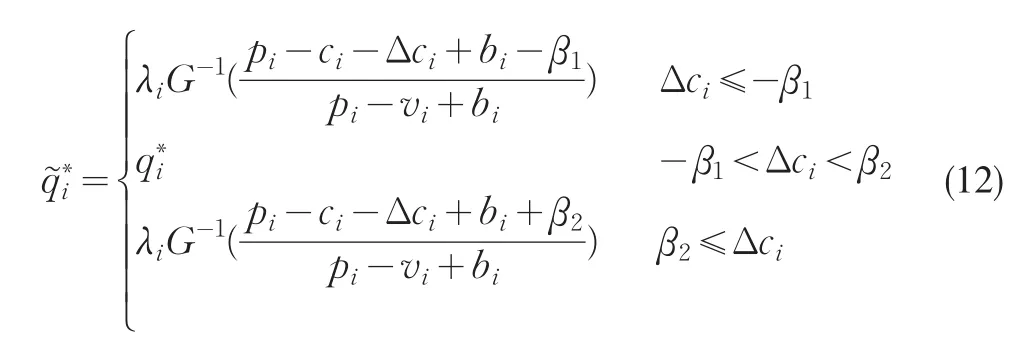
定理2说明在供应链竞争环境下,制造商的生产成本在小的范围内扰动时,可保持原生产计划不变,即具有鲁棒性。但当制造商的生产成本扰动范围较大时,决策者要对原生产计划进行调整,做出增大或减小生产规模的决定,且订货量随着自身市场份额的增大而增大,随着竞争对手的市场份额的增大而减小。
定理3 在供应链竞争环境下,当突发事件导致市场随机需求和生产成本同时扰动时,若Δci≤ Ωi,则若则其中,
由定理3可知市场规模的大小直接影响竞争供应链系统的决策,那么当市场规模增大或减少时供应链的决策发生的变化有如下推论。
推论2在供应链竞争环境下,如果突发事件导致市场规模增大,即Gi(q)≥Fi(q),对任意qi≥0,只要制造商的生产成本满足 -ci<Δci≤β2,则;如果突发事件导致市场规模减小,即Gi(q)≤Fi(q),对任意qi≥0,只要制造商的生产成本满足 Δci≥-β1,则
推论2表明,当市场规模增大时,供应商会通过采用适当的成本增大生产规模来应对需求的增加;当市场规模减小时,供应商会通过减小生产规模来应对需求的减小。
3.2 扰动发生后协调契约设计
我们已经获得了在生产成本和需求同时发生变化时的集权式供应链i的最优决策,但我们并不清楚回购加线性补贴加利润共享契约是否仍然可以协调需求和生产成本同时发生扰动下的竞争供应链,下面对这一问题进行探讨。
假设扰动后制造商i提供给零售商的回购加线性补贴加利润共享契约为有如下定理:
定理4在供应链竞争环境下,当突发事件导致分权决策供应链的市场规模和生产成本同时发生变化时,若制造商i采用调整的回购加线性补贴加利润共享契约则无论制造商 j采用何种契约形式,都能实现竞争供应链的完美协调。
证明:当供应链i的市场规模和生产成本同时发生变化时,采用回购加线性补贴加利润共享契约后,零售商i的利润为
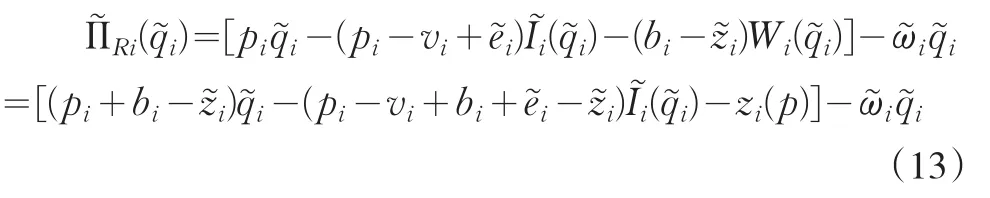
比较(9)式和(13)式可知,当
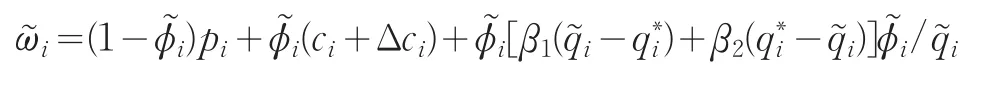

由定理4不难验证,当两供应链均采用回购加线性补贴加利润共享契约时,亦能达到供应链i的完美协调。
4 结论
以往对突发事件的研究主要集中在单条供应链系统中,通常只考虑需求是确定的。本文以竞争供应链为研究对象,研究了随机需求下突发事件导致市场需求和生产成本同时发生扰动的情形下竞争供应链的决策问题,并通过设计改进的回购加线性补贴加收益共享契约建立了协调机制。研究发现:当突发事件导致市场规模增加时,供应商会通过增大生产规模来应对需求的增加;当突发事件导致市场规模减小时,供应商会通过减小生产来应对减小的需求。另外,改进的回购加线性补贴加收益共享契约能使竞争供应链在突发事件下达到渠道最优利润,且能任意分配利润,即改进的回购加线性补贴加收益共享契约具有抗突发事件的特性。
[1] McGuire T W,Staelin R.An Industry Equilibrium Analysis of Down⁃stream Vertical Integration[J].Marketing Science,1983,(2).
[2] Moorthy S K.Strategic Decentralization in Channels[J].Marketing Sci⁃ence,1988,(7).
[3] Whang,S.Coordination in Operations:a Taxonomy[J].Journal of Oper⁃ations Management,1995,12(4).
[4] Chen F,A.Federgruen,Y.Zheng.Coordination Mechanisms for De⁃centralized Distribution Systems with One Supplier and Multiple Re⁃tailers[J].Management Science,2001,47(5).
[5] Cachon,G,Lariviere M.Supply Chain Coordination with Revenue Sharing Contracts[J].Management Sci.,2005,(51).
[6] 甘永辉,徐兵.供应链间的竞争与协调合同设计研究[J].南昌大学学报,2006,37(2).
[7] Zhao,X.,Shi,C.Structuring and Contracting in Competing Supply Chains[J].International Journal of Production Economics,2009,(11).
[8] Clausen J,Hansen J,Larsen J.Disruption Management[J].OR/MS Today,2001,28(5).
[9] Qi X T,Bard J,Yu G.Supply Chain Coordination with Demand Dis⁃ruptions[J].Omega,2004,32(4).
[10] Xu MH,Qi X T,Yu G,et a1.Coordinating Dyadic Supply Chains when Production Costs are Disrupted[J].IIE Transaction,2006,38(9).
[11] Xiao T J,Qi X T.Price Competition,Cost and Demand Disruptions and Coordination of a Supply Chain with One Manufacturer and Two Competing Retailers[J].The International Journal of Management Sci⁃ence,2008,36(5).
[12] Chen K B,Xiao T J.Demand Disruption and Coordination of the Supply Chain with a Dominant Retailer[J].European J of Operation⁃al Research,2009,197(1).
[13] 曹二保,赖明勇.需求和成本同时扰动时多零售商供应链协调[J].系统工程理论与实践,2010,30(10).

