基于偏最小二乘方法的信用评分模型

魏秋萍，张景肖

0 引言

在建立信用评分模型时，备选的自变量过多是一个非常突出的问题。尽管已经有比较成熟的变量选择方法如IV值、Gini指数等，但是使用这些方法做变量选择时仍有很多的自变量无法取舍，并且这些自变量之间往往存在着多重共线性。

当自变量之间存在多重共线性时，使用普通最小二乘法（Ordinary Least Squares）或者极大似然法（Maximum Likelihood Estimation）往往会放大模型的误差，弱化模型的预测精确度，使得模型的稳健性欠缺。这时一般采用偏最小二乘（Partial Least Squares，简称PLS）方法。其思想是通过对系统中的数据信息进行分解和筛选，提取最能解释因变量的主成分的手段来克服多元回归模型中常见的多重共线性问题。

偏最小二乘模型出现于上个世纪60年代，经济学家Wold H.[1]在给一些变量组拟合因果关系路径时首次使用该算法。Wold H.[2]等把偏最小二乘方法用于化学计量学中的变量降维来克服变量的多重共线性。Frank[3]等把偏最小二乘方法和主成分分析等方法进行比较，说明了偏最小二乘方法是一种有效的降维技术。在此后，偏最小二乘方法在各个涉及多元分析的领域有了广泛的应用。在国内，王惠文[4][5]对偏最小二乘思想展开了比较深入的研究，并应用该方法来解决实际经济问题。

本文将针对信用评分中的变量众多问题展开研究，并建立基于偏最小二乘方法的信用评分模型。

1 基于偏最小二乘方法的信用评分模型

线性回归模型用自变量的线性组合来解释因变量的变异，通过普通最小二乘法来估计函数中的各个参数。线性回归在参数估计中唯一的约束条件为：要使得对样本中因变量的预测误差最小。偏最小二乘回归模型是对线性回归模型的一个改进，该算法兼顾了因变量的变异和自变量的变异两个目标。

偏最小二乘回归参数估计的核心思想为：先从自变量中提取能够最佳解释因变量的主成分，再对这些主成分应用最小二乘法拟合线性回归模型，通过不断迭代得到偏最小二乘回归模型的参数估计值。

其中，T是根据自变量提取出来的主成分矩阵，对因变量具有最强的解释能力；Q是主成分矩阵T的回归系数矩阵；E为误差矩阵，代表了模型的噪音。上述模型也等价于：

对于某一个观测而言，其预测值为：

这里，H小于自变量X的维度d。

偏最小二乘算法抽取的潜在主成分不仅可以解释建模样本中因变量的变异，还可以解释自变量的变异。在信用评分模型中，因变量的取值是好客户还是坏客户是表现出来的特征，是度量客户风险大小的一个标识；而自变量如学历、婚姻、职业等也都是表现出来的特征。自变量往往并不是决定因变量的因素，真正决定客户好坏的本质特性是不可观测的潜在因素，如客户的偿还意愿、客户的偿还能力等。客户的偿还意愿是他的婚姻、学历教育和职业等特征综合出来的表现其道德修养的主成分，客户的偿还能力是他的收入、年龄和工龄等特征综合出来的表现其经济水平的主成分。基于这种业务特点，能够同时解释因变量和自变量变异的偏最小二乘模型在业务逻辑上更利于信用评分模型的创建。

1.1 限制预测值的偏最小二乘回归模型

基于偏最小二乘回归模型拟合模型和估计参数的独特思路，使得它更加能够解释信用评分模型要解决的业务问题。但是，该模型也存在着一定的局限性，必须对其做出一些修正才能应用于信用评分模型的创建。

一般来说，偏最小二乘模型适用于因变量为连续变量的情况，它估计出的预测值会在(-∞,+∞)这个范围内变化。在信用评分模型中，因变量是只有两种可能取值的属性变量，可以用0（表示好客户）和1（表示坏客户）来表示其取值。但是创建信用评分模型是为了得到每个申请人未来成为坏客户的概率，而不是直接预测因变量的值到底是1还是0。因此，如信用评分模型输出形式是预测概率P(yt=1|X)，它就可以被看成是一个连续变量，只是取值范围在0到1之间。这样只要根据偏最小二乘法的一般原理略加限制修改，就可以让其适用于信用评分模型。

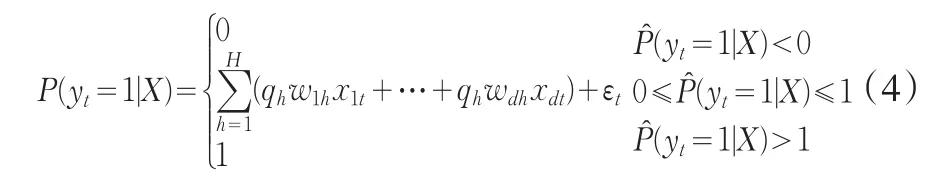
这样通过对偏最小二乘回归模型的预测值加以限制，就可以从技术上保证它可以应用于信用评分模型的创建。

1.2 偏最小二乘Logistic回归模型

为了使得偏最小二乘回归的思想能够适用于信用评分模型的创建，限制预测值的偏最小二乘回归模型从控制预测值的角度对模型做出了改进。除了这种改进思路以外，还可以结合偏最小二乘回归和Logistic回归的思想来解决信用评分模型的实际问题。这两种思想的结合产生了偏最小二乘Logistic回归模型，该模型是由V.E.Vinzi和M.Tenenhaus提出的[5]。

4.强化人才保障。一是要做好电子商务人才的引进工作，尤其要重视做好高端人才的引进工作，引进一批处于电子商务发展前沿、运行和管理经验丰富的优秀人才和团队。二是强化对电子商务人才的培训培养工作，注重发挥社会培训机构的作用，并加强与高校的战略合作，利用在渝高校的巨大人才资源优势，全方位培训电商从业人员，运用多种途径培养高级电子商务职业经理，打造一支高素质的电子商务专业人才队伍。三是探索完善电商人才“留住”机制，营造市内电商人才宜居宜业良好环境，为我市电子商务产业发展提供人才保障。

偏最小二乘Logistic回归模型的主要假设是：事件发生的概率的Logit变换可以用主成分来解释，而这个主成分综合了自变量的信息，也可以解释自变量的变异。把偏最小二乘Logistic回归模型应用于信用评分模型，则可以表示为

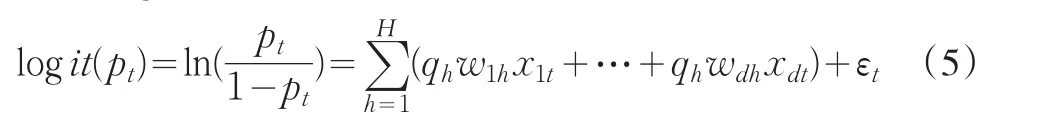
这里 pt=P(yt=1|xt)表示一个申请人在未来成为坏客户的概率。偏最小二乘Logistic回归等价于Logistic回归加上偏最小二乘回归模型，它兼顾了两种模型的优点。不管从技术的角度还是从业务的角度分析，源自偏最小二乘思想的偏最小二乘Logistic回归都非常适用于创建信用评分模型。偏最小二乘方法用影响因变量和自变量的潜在因子来解释模型，不但能解决信用评分模型中常出现的变量共线性问题，也更符合业务逻辑,必然在信用评分领域发挥独特的作用。

2 实证分析

针对某商业银行信用卡的实际数据，分别利用Logistic回归、神经网络、支持向量机、决策树、限制预测值的偏最小二乘回归和最小二乘Logistic回归这六种建模方法分别创建信用评分模型，并比较它们所得的预测结果。评判各个模型预测结果的优点和不足将依据模型在训练集、测试集和样本外验证集上的性能表现。源自实际数据的建模样本中共有24583条观测，25个自变量和1个因变量。样本中好坏客户所占的比例分别为96.75%和3.25%。可以把建模样本中60%的观测选择作为训练集，用于模型的创建；选择剩下的40%的观测作为测试集，用于样本内的测试和评价。在分割训练集和测试集的时候采用分层抽样的方法来保证训练集和测试集中好坏客户的占比和原来样本中的占比保持一致。同时，还选择了一个从其它时间段获得的记录数为14750条的样本外验证集来评价模型的准确性和可推广性，该数据集中的观测和建模样本中的观测完全不重合。样本外验证集中的好坏客户的占比也是96.75：3.25。

实证分析的具体结果如表1。

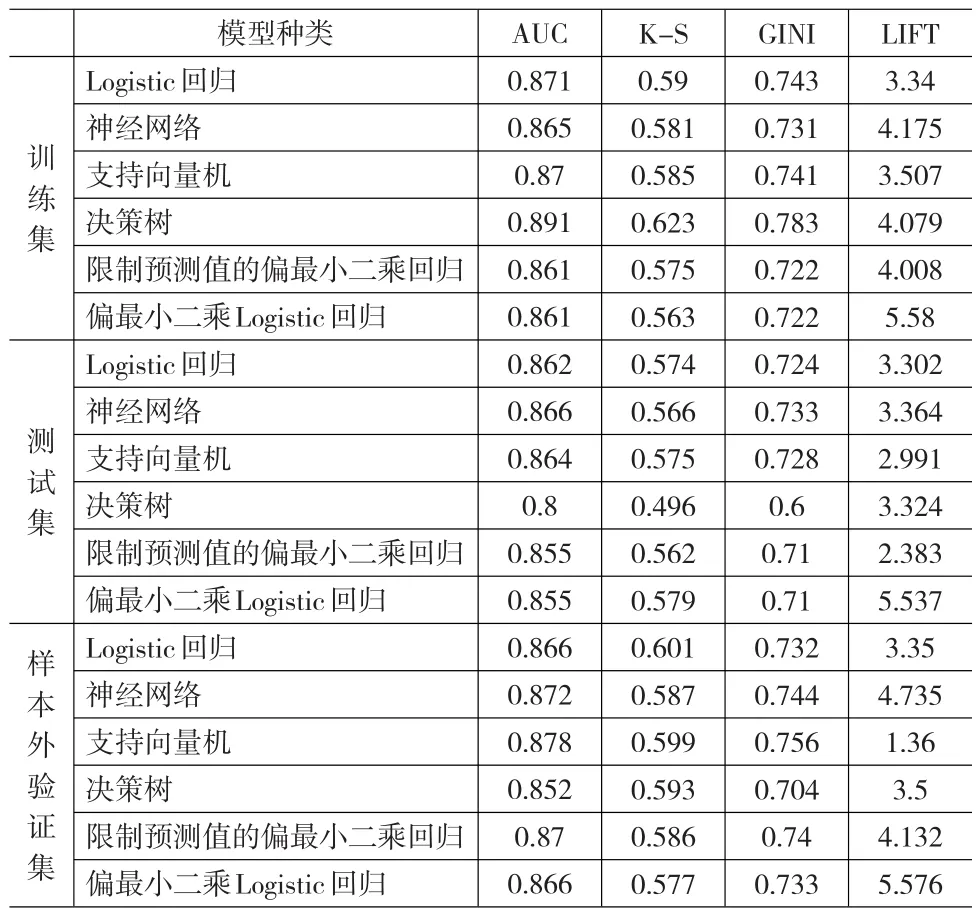
表1 各种评分模型建模方法的实证分析结果

由上面的结果可知：

（1）Logistic回归模型创建的信用评分模型在训练集、测试集和样本外验证集的AUC统计量分别为0.871、0.862和0.866，K-S统计量分别为0.59、0.574和0.601，GINI系数的值分别为0.743、0.724和0.732，Lift值分别为3.34、3.302和3.35。训练集的评价统计量取值略优于测试集和验证集的取值，并且这些统计量相对比较稳定。这说明了Logistic回归模型具有稳定性的优点。

（2）神经网络模型创建的信用评分模型在训练集、测试集和样本外验证集的AUC统计量分别为0.865、0.866和0.872，K-S统计量分别为0.581、0.566和0.587，GINI系数的值分别为 0.731、0.733 和 0.744，Lift值分别为 4.175、3.364和4.735。这些统计量的值相对比较大，表明了模型有较好的预测准确性。一般情况下，都是训练集的评价统计量要优于测试集和样本外验证集的，但是样本外验证集的验证统计量普遍要高于测试集的，这在一定程度上也表明了神经网络并不是很稳定性的算法。

（3）支持向量机算法创建的信用评分模型在训练集、测试集和样本外验证集的AUC统计量分别为0.87、0.864和0.878，K-S统计量分别为0.585、0.575和0.599，GINI系数的值分别为0.741、0.728和0.756，Lift值分别为3.507、2.991和1.36。尽管AUC、K-S统计量和GINI系数表现出了较好的稳定性，但是支持向量机算法的LIFT值相对不稳定，这也说明了该算法有微弱的不稳定性。

（4）决策树的结果相对不理想，它在训练集中有很好的性能表现，AUC、K-S统计量和Gini指数都是最高的，但是到了测试集中这三个指标都是最低的，决策树模型在样本外验证集中的表现也是相对比较差的。这些结果表明用决策树创建信用评分模型得到的结果最不稳定。

（5）限制预测值的偏最小二乘回归模型创建的信用评分模型在训练集、测试集和样本外验证集的AUC统计量分别为0.861、0.855和0.87，K-S统计量分别为0.575、0.562和0.586，GINI系数的值分别为0.722、0.71和0.74，Lift值分别为4.008、2.383和4.132。只有测试集的LIFT值相对偏小，其他统计量的表现都比较稳定。这也说明限制预测值偏最小二乘回归模型具有稳定性的优点。

（6）偏最小二乘Logistic回归模型创建的信用评分模型在训练集、测试集和样本外验证集的AUC统计量分别为0.861、0.855和0.866，K-S统计量分别为0.563、0.570和0.577，GINI系数的值分别为0.722、0.71和0.733，Lift值分别为5.58、5.537和5.576。各个验证集上的验证统计量都保持了稳定的特点，这说明了偏最小二乘Logistic回归模型具有稳定性的优点。同时，该模型的Lift值和其他模型相比取值更大更加稳定，这表明偏最小二乘Logistic回归在识别最坏的坏客户的能力要优于其他算法。

总而言之，以上六种建模方法均可用来创建信用评分模型，除了决策树以外，其他五种建模方法创建出的模型效果各有优劣。实证研究的结果也表明，限制预测值的偏最小二乘回归和偏最小二乘Logistic回归模型这两种基于偏最小二乘思想的信用评分模型具有良好的预测效果，值得进一步推广。

3 结论

信用评分模型的建模方法不拘一格，现代常用的统计模型和机器学习算法都可以用来创建信用评分模型。每一种建模方法各有优缺点，在使用的过程中必须根据实际需要来决定选用哪一种算法。同时，采用不同的建模方法来创建信用评分模型可以互相验证彼此的准确性。本文提出的限制预测值的偏最小二乘回归模型和和偏最小二乘Logistic回归模型用潜在的因子同时解释了因变量和自变量的变异，在实际运用中具有很好的可操作性，实证分析的结果也表明，用这两类这两种基于偏最小二乘思想的信用评分模型具有比较好的性能表现。

[1] Wold,H.Estimation of Principal Components and Related Models by Iterative Least Squares[A].In P.R.Krishnaiah,ed.Multivariate Analy⁃sis[C].New York:Academic Press,1966.

[2] Wold,H.Soft Modelling by Latent Variables:the Non-linear Iterative Partial Least Squares(NIPALS)Approach,Papers in Honor of M.S.Bartlett[C].Academic Press,London,1975.

[3] Frank,I.E.,Friedman,J.H.A Statistical View of Chemometrics Re⁃gression Tools[J].Technometrics,1993,(35).

[4] 王惠文.偏最小二乘回归方法及其应用[M].北京：国防工业出版社,1999.

[5] 王惠文等.偏最小二乘回归的线性与非线性方法[M].北京：国防工业出版社,2006.