贝叶斯假设检验与经典假设检验的对比研究

张 静

0 引言

显著性检验在经典统计中作为统计推断重要内容之一，被广泛应用在各个领域。显著性检验是通过样本信息对总体的某个假设做出拒绝或不拒绝的决策，是用推断的方法解决决策的问题，不能给出决策错误时所产生的损失大小，并且在使用显著检验过程中出现一系列问题。相比之下贝叶斯检验方法能较好的处理这些检验问题。

1 经典检验结果的不确定性

经典假设检验首先根据问题的要求提出假设，通过给定的显著水平确定检验的拒绝域，然后根据样本是否落入拒绝域来判断拒绝还是接受原假设。但是，在实践中由于假设的建立不同、显著水平α大小不同，往往会出现同一问题和同一组样本数据得到完全相反的检验结果，使得检验所得的“显著”结果在实际中并无重大意义。

假如有一组调研人员做了一个关于总体均值在0.12处的单侧Z检验,显著水平α=0.05，获得抽样结果z=0.015，若假设为 H0:μ≤0.12, H1:μ＞0.12，由于拒绝域为{z ≥1.645}，而z=0.015＜1.645,z值没有落入拒绝域故认为总体均值不大于0.12。然而若假设变为H0:μ≥0.12, H1:μ＜0.12时，其拒绝域为{z ≤-1.645} ，而z=0.015＞-1.645,z值没有落入拒绝域，即认为总体均值不小于0.12，与上述的结论是相反的。

一个双尾检验变为单尾时，检验结果有可能超越“统计显著”的界限。假如我们做了一个双尾Z检验，获得抽样结果z=1.85,检验p值≈0.06，当α=0.05时检验结果是不拒绝原假设，即不显著。将检验改为单尾时，单尾检验p值比双尾检验p值缩小一半，检验结果立即变为显著的了。若将显著水平α增大到0.07时双尾Z检验又变为显著了。

相比之下，贝叶斯检验中，无论如何建立假设，也无需给出显著水平，只要给出参数的后验分布，通过计算各假设的后验概率，对假设的后验概率大小的比较，就可以得到确切的检验结果，即检验结果是稳定的。

2 经典检验中显著水平的误导

在经典假设检验中，p值越小，意味拒绝H0的证据越充分。但事实上经典检验中p值常常是高估拒绝H0的证据。当样本容量很大时，抽样结果与H0的微小差别，总能得到一个极小的p值，导致拒绝H0的结论，然而这个结论并没有实际意义。即便是在中等样本量时，一个小的p值也几乎不提供拒绝H0的证据，即经典的犯错误的概率或显著性水平，把原假设是否有效引导到完全错误的印象中去。

例如，假设观测样本 X1,X2,…,Xn来自分布N(θ,σ2)，σ2已知。检验假设 H0:θ=θ0,H1:θ≠θ0，采用贝叶斯方法进行检验。给θ先验分布为：在θ=θ0时π0=π(θ0)=1/2，在 θ≠θ0时 π(θ)=π1g1(θ)，其中 π1=1-π0=1/2,g1为 N(μ,τ2)，当给出先验的具体值 μ=θ0,τ=σ时，可给出不同样本容量n及不同抽样结果下的p值及α0如下表。

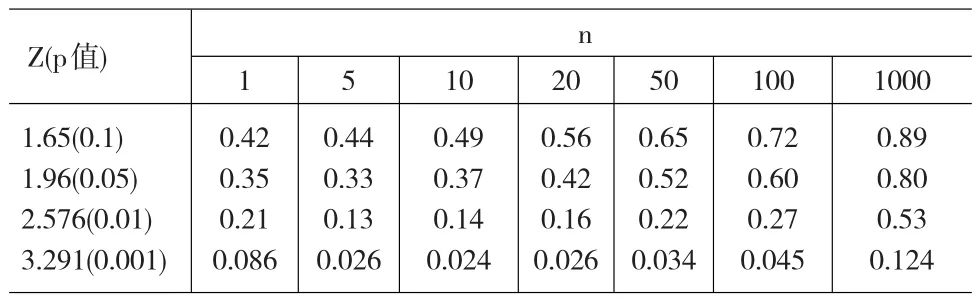
Z(p值)n 1 5 1.65(0.1)1.96(0.05)2.576(0.01)3.291(0.001)0.42 0.35 0.21 0.086 0.44 0.33 0.13 0.026 10 0.49 0.37 0.14 0.024 20 0.56 0.42 0.16 0.026 50 0.65 0.52 0.22 0.034 100 0.72 0.60 0.27 0.045 1000 0.89 0.80 0.53 0.124

从表中的数据可以看出若由观测值得z=1.96,意味经典检验中拒绝H0的显著水平是0.05，由于0.05够小，拒绝H0的证据看似足够充分，所以结论是拒绝原假设。然而，H0的后验概率是很大的，从小的n时的1/3，到大的n时接近1。即当p值为0.05时几乎不提供拒绝H0的证据。同时可以证明，对任何合理的先验，在同一组样本数据下，经典检验中的较小的p值都对应较大的后验概率α0。于是，出现了经典犯错误的概率或p值对否定H0的根据进行完全错误的描述[1]。

3 经典最优与贝叶斯方法的等价性

假设观测样本 X1,X2,…,Xn来自分布 N(θ,σ2)，σ2已知，π(θ)～ N(μ,τ2)，考虑检验 H0:θ≥θ0, H1:θ＜θ0，若以“0—Ki”为损失函数，则可得贝叶斯检验的拒绝域为：，其中与经典的α水平、一致最大功效检验的拒绝域具有相同的形式。在经典检验中拒绝域的临界值由α决定，而在贝叶斯检验中则由损失和先验信息决定。结论是：（1）经典检验中α选取没有准则，通常为0.05或0.01，但这个惯例并没有严格地被大多数统计学家严格遵守，α的选择具有主观性；（2）经典犯第一类错误概率α不能说明犯错误时所产生的损失的大小；（3）每一α水平的最大功效检验相对应一个贝叶斯检验，即或者对假设的先验及损失做主观选择或者对α水平做主观选择；（4）贝叶斯方法充分运用了合理的先验信息及抽样信息，并且给出决策错误时的损失，其结论更加可靠，因而贝叶斯方法可以看作是提供了一个选择检验的显著水平大小的合理方法。

4 经典检验不宜处理多个假设的情况

对于问题 H0:θ∈Θ0↔H1:θ∈Θ1若 Θ0⋃Θ1≠Ω（Ω为参数空间），假设检验中常常存在两者皆可的区域，即产生第三个假设θ∈Θ2。例如，若要求检验两种药物的治愈率 ，合 理 的 方 法 是 三 个 假 设 ：H0:θ1-θ2＜-ε，H1:θ1-θ2＞ε H2:| θ1-θ2|≤ε，其中 ε＞0 的选择是认为|θ1-θ2|≤ε为两种药是等效的。经典假设检验中常处理的情况是非此即彼，对这类问题无法定义p值；另外，当检验涉及三个及三个以上的多重比较问题，经典的检验将增加犯第一类错误的概率，所以，经典假设检验方法亦不宜处理多重假设问题，而贝叶斯假设检验通过计算每一个假设的后验概率，接受后验概率最大的假设。因此，贝叶斯方法更易处理多个假设的检验问题。

5 结论

无论是经典假设检验，还是贝叶斯假设检验，人们关心的问题是假设检验的结果是否真能反应原假设的真伪，但以“显著水平”为中心的经典假设检验理论并不能直接回答这个问题。本文通过对两种检验方法的对比研究，指出了经典检验方法存在的一些问题，以及贝叶斯检验方法在解决这些问题时的优势。

[1] [美]James O.Berger.统计决策论及贝叶斯分析[M].北京：中国统计出版社,1998.

[2] 傅军和.经典检验p值的若干问题[J].统计与决策，2009,(1).

[3] 茆诗松.贝叶斯统计[M].北京：中国统计出版社，1999.

[4] 韦博成.参数统计教程[M].北京：高等教育出版社，2006.