两类错误条件下方差检验中样本容量的确定

郭 文

0 引言

样本容量是指按照某种规则从总体中抽取出来的样本观察单位的数目。在抽样调查中，样本容量的研究是一个非常重要的问题,样本容量直接影响着犯两类错误的概率。在假设检验中，一般讨论的是犯第一类错误的情况，通常只给出犯第一类错误的概率，那么在样本容量自由选择的情况下，犯第二类错误的概率是无法控制的。而犯第二类错误的情形一般在医学、风险控制、质量控制等领域应用较多。在研究这些领域时，我们希望能同时控制两类错误的概率，那么样本容量就需要通过计算来确定。目前国内外对样本容量的研究大多是建立在调查精度和费用控制的基础上。本文研究样本容量的角度与之不同，是在控制两类错误的前提下，对方差检验中样本容量进行探讨。

1 两类错误的概念

如果把假设检验中构造的统计量记为T，把显著性水平α下确定的拒绝域记为，把接收域记为W，则当T服从正态分布时，双侧检验的与W如图1所示。图中阴影部分为拒绝域，非阴影部分为接受域W。

当原假设H0为真时，由于样本的随机性，仍然有可能以α的概率拒绝原假设H0,这就是第一类错误，简称弃真，α为弃真的概率。如图1，弃真显然就是H0为真时T落入拒绝域Wˉ的事件，所以

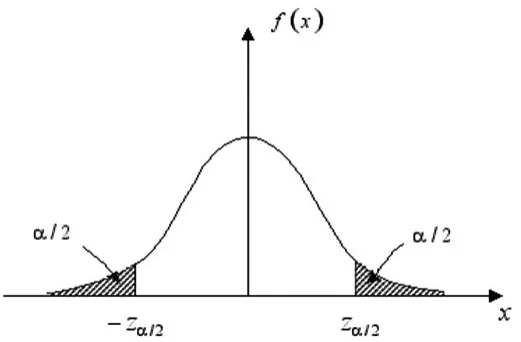
图1 双侧检验的拒绝域与接收域

当原假设非真时，我们也仍然有可能接受它，这就是第二类错误，简称取伪，取伪的概率以β表示。取伪显然是当H0为非真时，T落入接受域W的事件，所以

P{T ∈ W| H0非真} =β

2 单母体情形下样本容量的确定

2.1 μ已知

设随机样本(X1,X2,…,Xn)来自正态总体X～N(μ,σ2)，μ=μ0已知。

对于右侧检验，首先建立假设检验：

其次构造χ2统计量：

当H0为真时：

当 H1为真时：

根据定义，有

因此

uα、uβ为标准正态分布的上α分位点、β分位点。

将式（2）、（3）代入式（1）得：

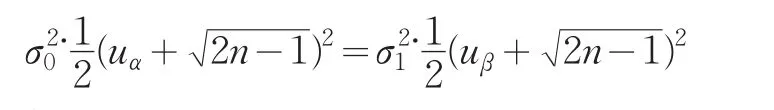
解得：

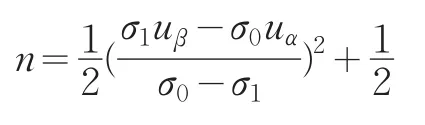
同理，可计算出左侧检验样本容量为：

双侧检验时样本容量为：

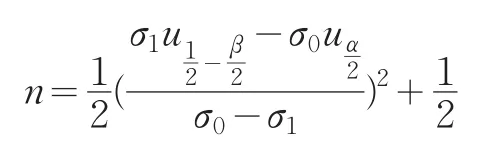
2.2 μ未知

设随机样本(X1,X2,…,Xn)来自正态总体 X～N(μ,σ2)，μ未知。

对于右侧检验，首先建立假设检验：

构造χ2统计量：

当H0为真时

当H1为真时

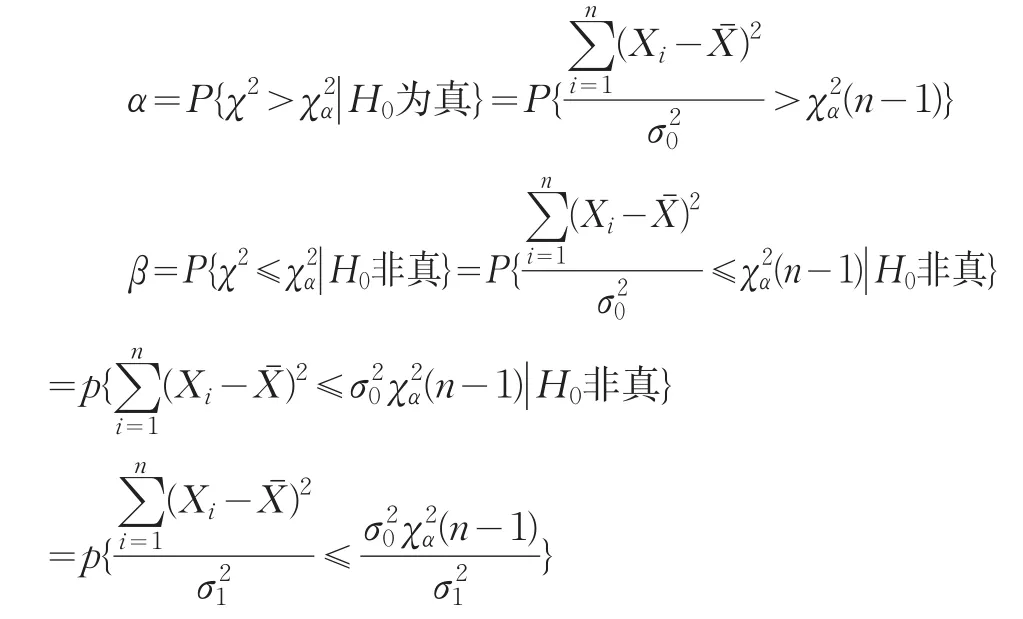
因此

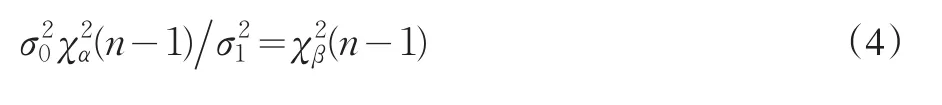
同样，当n充分大时（通常n＞45），有

这里uα、uβ为标准正态分布的上α分位点、β分位点。

将式（5）、（6）代入式（4）得：

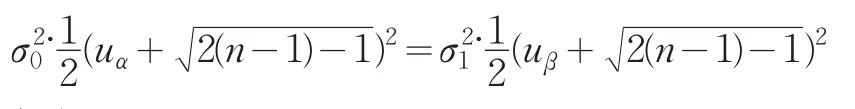
解得

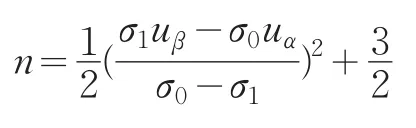
同理，可计算出左侧检验样本容量为：

双侧检验时样本容量为：

3 双母体情形下样本容量的确定

3.1 μ1、μ2已知

设 X1,X2,…,Xm和Y1,Y2,…,Yn是分别从服从和分布的两个母体中抽出的独立子样，μ1、μ2已知。

首先建立假设检验：

其次构造F统计量：

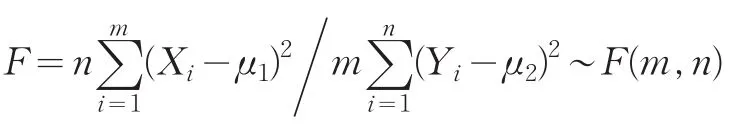
对于右侧检验，建立假设检验：

则

则

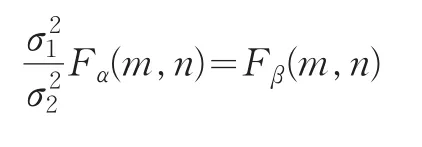
当n→∞时，有 Fα(m,∞)=

又因为

因此

同理

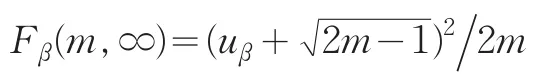
所以，当n→∞时，有

解得：

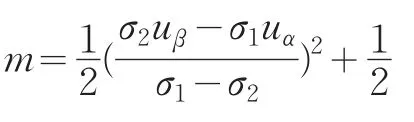
同理，可计算出左侧检验时样本容量为：

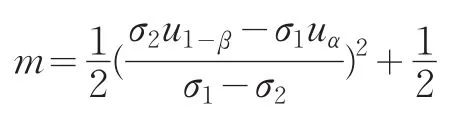
双侧检验时样本容量为：

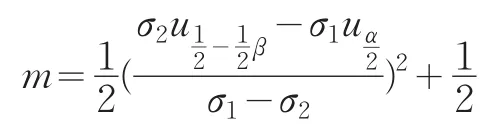
3.2 μ1、μ2未知

设 X1,X2,…,Xm和Y1,Y2,…,Yn是分别从服从和分布的两个母体中抽出的独立子样，μ1、μ2未知。

首先建立假设检验：

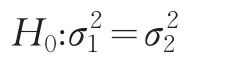
其次构造F统计量：

当H0成立时，F∼F(m-1,n-1)。

对于右侧检验，建立假设检验：

则

则

当n→∞时，有 Fα(m-1,∞)=

又因为

因此

同理

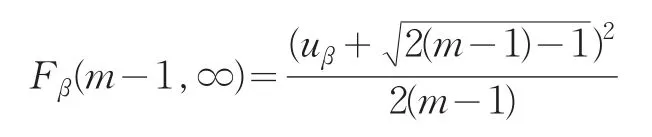
所以，当n→∞时，有

解得：

同理，可计算出左侧检验样本容量为：

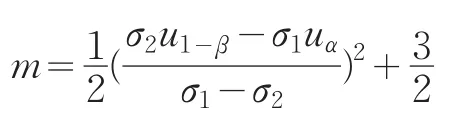
双侧检验时样本容量为：

4 结论

以上我们对方差检验中单母体及双母体方差已知、方差未知情形下两类错误与样本容量的关系进行了探讨，并在控制两类错误的条件下，给出了确定样本容量的公式。从上面的讨论可以看出，方差检验中样本容量的确定是件比较复杂的事情，必须给予足够的重视。在实际操作中，样本容量的确定既要考虑精度要求，又要考虑经费预算、可操作性等，必须通过综合考虑，以达到一个最优样本容量的选择。

[1] 陈国铭，李世英.统计质量控制：估计和检验[M].北京：中国石化出版社，北京,1995.

[2] 陈希孺.概率论与数理统计[M].合肥：中国科学技术大学出版社，2009.

[3] 魏宗舒.概率论与数理统计教程（第二版）[M].北京：高等教育出版社，2008.

[4] 冯士雍，施锡铨.抽样调查——理论、方法与实践[M].上海：上海科学技术出版社，1994.

[5] W.G.Cochran.Sampling Techniques[M].Chichester:John Wiley&Sons，1997.