基于网络质量控制的复杂供应链网络稳健性研究

徐 兴 李仁旺 吴新丽 刘海霞

1.浙江理工大学，杭州，310018 2.浙江科技学院，杭州，310023

0 引言

近年来，Internet、交互式Web应用及电子商务的出现彻底改变了传统的供应链结构模式，多层的供应链结构已转变为基于Internet的开放式全球供应链网络。目前，国际上以Dirk Helbing为首的一批科学家在采用复杂网络理论研究供应链网络时发现，供应链管理中的牛鞭效应与网络的拓扑结构性质有关［1－2］，因此构建一个具有稳健性的供应链网络，是实现复杂供应链网络管理的基础和关键。

国内外关于复杂供应链网络的研究主要集中在基于复杂系统理论的供应链适应能力分析和供应链企业节点间知识共享等方面［3－4］，但都没有考虑到复杂供应链网络的拓扑结构性质。基于网络图论的复杂供应链网络建模研究知识清楚地展示了供应链网络内各企业节点之间的关系［5］，但无法清楚地表明供应链网络的稳健性和脆弱性。文献［6－7］分别建立了随机需求下的供应链鲁棒性设计模型和干扰事件风险下的可靠供应链系统设计模型，但事实上，供应链网络的稳健性不仅与供应链中节点企业的稳定性有关，还与供应链网络的结构有关。

目前尚未见到对复杂供应链网络的拓扑结构和演化过程中稳健性的专门研究，一般都只是依据复杂网络的性质，指出其稳健性和脆弱性［8］。本文运用复杂网络理论，以图论和社会网络分析的网络静态几何量及其分析方法为基础，对复杂供应链网络进行建模分析，同时结合质量统计学的原理与分析方法，从网络质量控制的角度来研究复杂供应链网络拓扑结构的几何性质、结构的稳健性以及网络演化过程中的动态稳健性。

1 复杂供应链网络的构建方法

1.1 网络拓扑结构的构建方法

从复杂系统科学的视角出发，供应链系统的形成、发展和变化都可以看作是供应链系统内各组成要素及其与外部环境相互作用的结果。因此供应链系统不只是单个企业的供应链，而是一个盘根错节的多层产业供应链网络［9］，其构建方法如下：将供应链中不同的企业实体作为网络的节点，将企业之间的联系作为网络的边，边的方向从供应链中上一级企业指向下一级企业，边的权重为父节点及其子节点的数目，如图1所示。

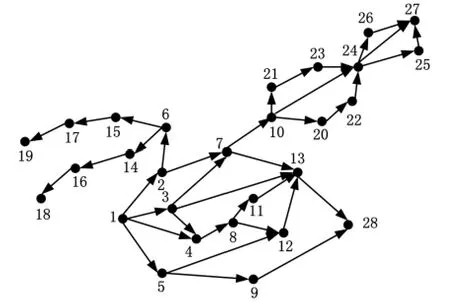
图1 供应链网络拓扑结构图

1.2 无标度供应链网络的形成

在网络拓扑结构图中，节点的入度是指指向该节点的边的条数，节点的出度是指从该点出发的边的条数，这里假设x表示企业合作复杂网络的节点，r表示该网络节点之间的边。i、j为网络中任意的两个节点，如果i和j之间存在边，即i企业和j企业存在合作关系，令r（i，j）＝1。假设网络中的节点i有ki条边，则相应的复杂网络中企业合作的静态统计量定义如下：

两点之间的距离

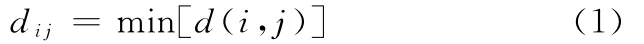
式中，d（i，j）为节点i、j之间的距离。

节点的度

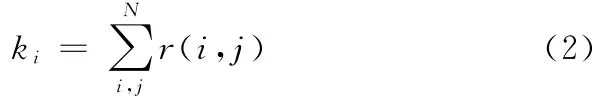
式中，N为网络中节点的总数。

节点的聚类系数

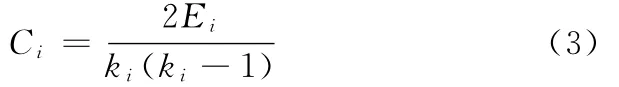
式中，Ei为与节点ki实际相连的边数。

根据构建的供应链网络拓扑结构图，编制网络处理程序，运用式（1）～式（3）便可求得网络各节点的上述统计量特征值，以进一步分析网络的各种特性。假设某供应链网络中的节点的度ki如表1所示，运用式（3）可求得这些节点的聚类系数Ci（表1）。

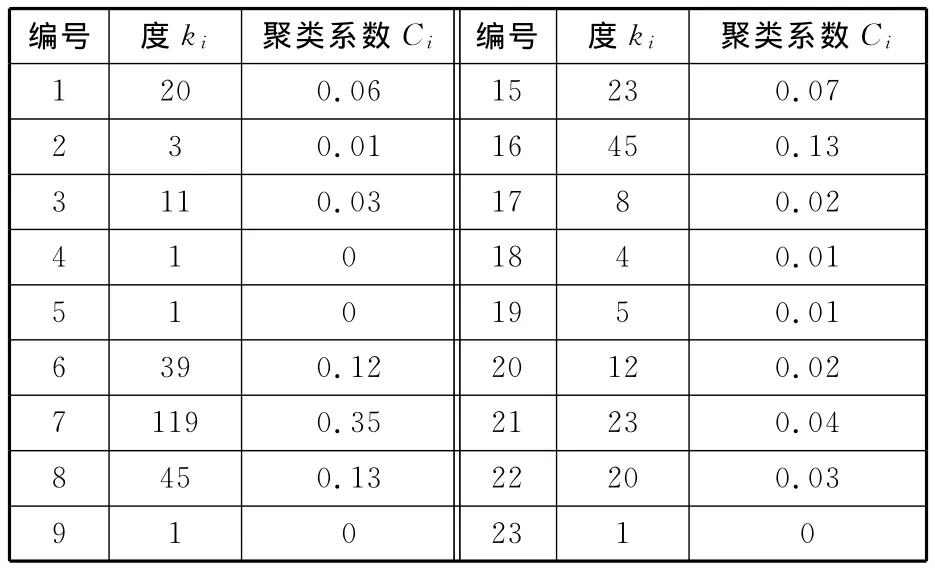
表1 节点的度和聚类系数

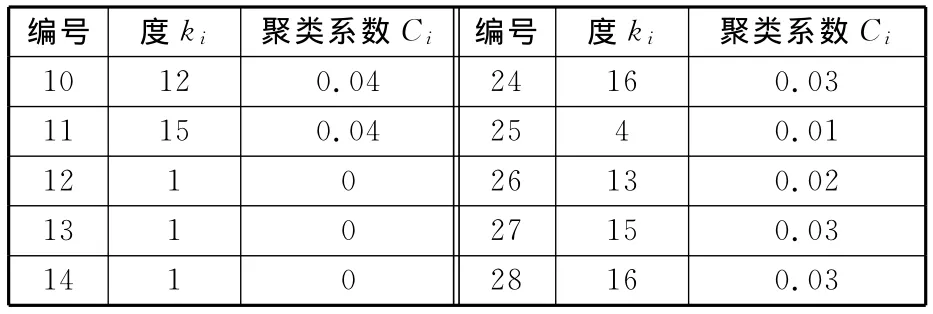
续表1

通过对上述供应链网络中各节点的聚类系数的计算，可发现该供应链网络中某些具有较大节点度的节点同样具有较大的聚类系数；再对每个节点的度的分布概率进行统计，发现该网络中大多数节点拥有少量的连接，而少数节点则拥有大量的连接，而且其节点的度的概率分布并没有峰值，这说明其节点的度分布服从幂律分布，符合无标度网络的特性，如图2所示。

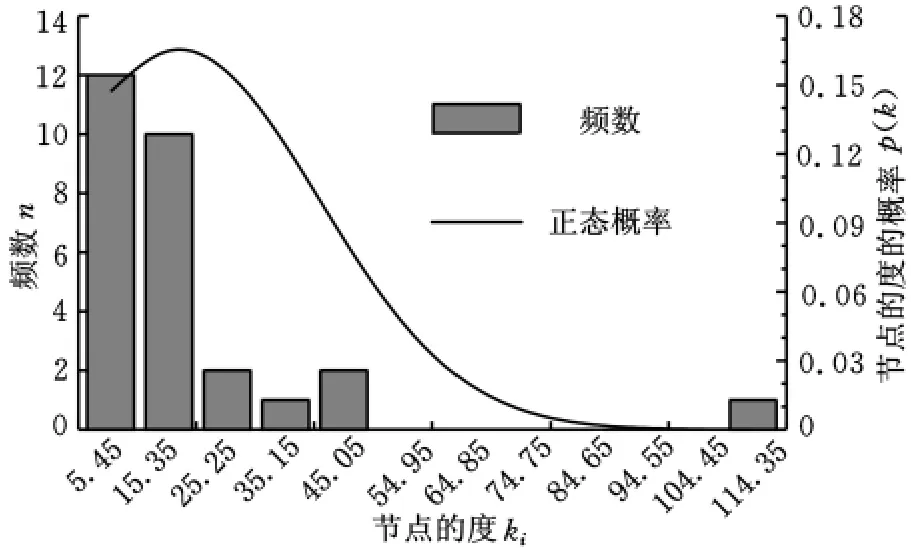
图2 节点的度的概率及分布

此外，随着网络的不断扩大，新的节点（图3的实心节点）倾向于连接已经有多个连接点的原节点（图3的空心节点），这样经过充分长时间的演化后，供应链网络中节点的度的分布将不再随时间变化，从而形成无标度供应链网络。

图3 无标度供应链网络形成过程示意图

2 无标度供应链网络稳健性分析

2.1 全球化供应链网络的模式及特征

互联网技术的快速发展和全球经济一体化使企业的采购和销售得以在全球范围内进行，出现了设计、采购、生产、配送和销售等业务遍及全球的供应链运作及管理模式。但是，全球化供应链面临着更大的不确定性，从而使供应链上的企业面临更大的风险。因此，在进行供应链网络结构设计时，必须充分考虑到网络的稳健性。

传统的供应链管理大都面向制造业产品，然而，在终端产品与内容服务的融合成为一种趋势以后，硬件和功能将不会再成为产品关注的焦点和瓶颈，未来发展的重点和主要竞争领域将是产品与内容的融合。如2011年，苹果公司成为全球第一大上市公司，这除了它不断创新之外，其稳健的供应链网络设计也为它的成功提供了坚实的保障，苹果公司稳健的供应链网络主要表现在：①苹果公司集中了全世界最优秀的部件和服务供应商来满足其大量的生产需求，供应商无法扩充产能来供应其他企业，这样供应链网络中的一些重要供应商（网络中的核心节点）就不会受到其他企业高利润的诱惑，从而影响供应链网络的稳定性；②苹果公司为供应商支付工厂建设费用，以此换取新零部件的采购权，并且在新的生产线实现大批量生产后，进行大量采购，这样就不会导致供应商由于资金短缺，不再生产某种型号的产品零部件，从而退出供应链网络。因此，为了保证供应链的稳定和正常运行，企业必须针对各种风险及其特征进行及时分析，采取不同的防范策略，保证供应链运行状况时刻处于有效的监控状态。

当企业把其供应链向国际延伸时，就会面临如何设计全球化供应链网络的问题，网络中节点的结构决定了整个供应链网络结构的复杂程度和稳定程度。Albert等［10］指出，无标度网络包含一些重要节点（这些节点的存在使网络既对随机失效具有稳健性，同时又具有易于被攻击的脆弱性），但并没有给出这些重要节点的相关定义。许多专家学者都对无标度网络进行了研究，通过对一些数据的计算，在实际复杂网络中发现了无标度网络的特性。但到目前为止，无标度网络尚无较严格的定义，并且相关文献也没有给出严格的理论依据［11］。因此，本文从网络质量控制的角度直观地定义供应链网络增长的无标度特性，明确网络的中枢节点及稳健性供应链网络的概念，并对无标度供应链网络动态增长过程中的稳健性进行分析。

2.2 无标度供应链网络的中枢节点

复杂供应链网络的稳健性可解释为：网络中某一节点遭受破坏时，仍能继续维持其运转能力，而不会对整个网络造成重大影响。如果网络中的某一节点在遭受外部随机攻击时，使网络发生灾难性故障，则称此节点不合格。按照质量控制的原理，只有当络节点的不合格率都小于某个预先期望的数，这样的网络才具有一定的稳健性。根据这个原理，首先给出无标度供应链网络中枢节点的定义：（V（t），E（t））表示一个随机的复杂供应链网络，V（t）为供应链网络在时刻t的节点集，即在供应链中的全部企业的集合，E（t）为在时刻t企业节点的边集，N（t）为网络在时刻t的企业个数，E（N（t））为网络在时刻t的企业平均数，ki（t）为企业i在时刻t的度。P｛ki（t）＝k｝（k＝1，2，…）表示企业i在时刻t的瞬态度分布。

无标度供应链网络中枢节点的定义为：如果A、B是V（t）的 两 个 真 子 集，A≠ ∅，B≠∅，A，B⊂V（t），且A∪B＝V（t），A∩B＝∅，存在K＞0，当k≥K时，∀t＞0，∀i∈A，j∈B，使得P｛ki（t）≥k｝＞P｛kj（t）≥k｝，则称A为无标度供应网络的中枢节点，这些节点即供应链中的某些核心企业。

2.3 稳健性供应链网络

稳健性供应链网络中的部分节点或边遭到随机破坏时，仍能够继续维持其功能。记p（t）＝｜A｜/E［N（t）］，｜A｜为集合A的势，若p（t）＜ε成立，ε∈ （0，1），则称该网络的中枢节点不合格率小于预先期望的数ε，那么这样的无标度网络（V（t），E（t））具有一定的稳健性。这里，为了方便统计分析，往往采用供应链网络中各节点的度来进行稳健性统计分析。在供应链网络中，中枢节点往往具有较高的度，但如果超出一定的范围，一旦这些节点受到攻击，将会使整个网络产生故障。按照质量控制的原理，当然是希望网络中全部节点的度都在安全阈值内，这样的网络才具有一定的稳健性。

本文借鉴质量控制中SPC（statistical process control）的原理，运用应用数学统计分析理论对供应链网络中各节点的度的分布情况随时进行监视和控制，实现对供应链网络节点度分布的实时管制，以减少供应链网络结构稳健性的变异［12］。一旦发现有网络中枢节点发生异常情况，即节点的度超过安全阈值σ，则立即采取措施进行调整，从而保证整个供应链网络能够稳定运行。

安全阈值σ分为控制上限σUCL和控制下限σLCL；设所有节点的度的平均值为T；控制上限σUCL＝T＋A2R，控制下限σLCL＝T－A2R。其中，R为每个节点的度的极差平均值；A2为常数，R、A2随样本容量n的不同而不同，参数值见Xbar－R系数表。由表1中的n＝28，查得A2＝0.729。

因此，对表1所示供应链网络中各节点的度分布情况，运用SPC分析软件中的测量系统分析（measurement system analysis，MSA），对27个子组进行试验统计，可得控制系数为0；控制参数的上下限均为20.89；稳定性判断的平均值超控制限数为27，基于超控控制限的判断为不可接受，图4为稳定性分析图，从中可随时查看网络中哪些节点超出了控制界限范围。

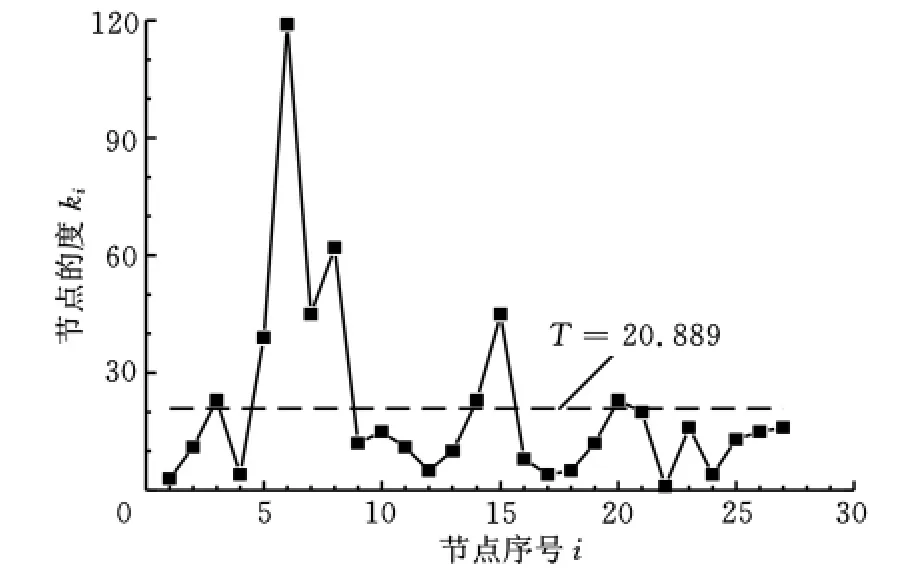
图4 稳定性分析图

3 供应链网络动态增长过程中的稳健性分析

3.1 网络增长过程中的稳态度分布

文献［5］指出，供应链网络随机增长过程P（t）服从参数λ的Poisson过程。Poisson模型满足以下两个条件：

（1）随机增长。假设刚开始的网络中已有m0个企业，新企业的加入服从参数λ的Poisson过程。当一个新的企业进入该供应链网络时，新企业具有的m（m＜m0）条边将会连接到已经存在于网络中的各个企业节点。

（2）择优连接。在选择新企业节点的连接时，连接概率Π取决于节点i的度ki，即满足

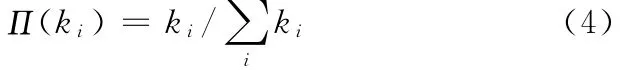
因为供应链网络中节点的到达过程P（t）服从参数λ的Poisson分布，所以当t充分大时，P（t）就可代表在t时刻到达网络的节点数，因此

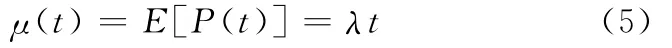
假定ki是连续实值变量，由于ki的变化率正比于概率Π（ki），因此满足动态方程：

其中，网络的平均度为2m。因此当t充分大时，有

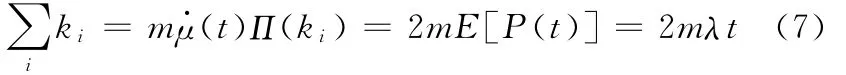
将式（7）代入式（6）得

由定义可知ki（ti）＝m，解方程（式（8））得

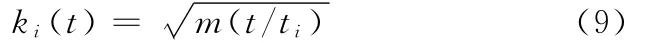
式中，ti为第i个企业进入网络的时刻。

由式（9）得

因为节点达到的过程服从参数λ的Poisson过程，因此节点达到的时间服从

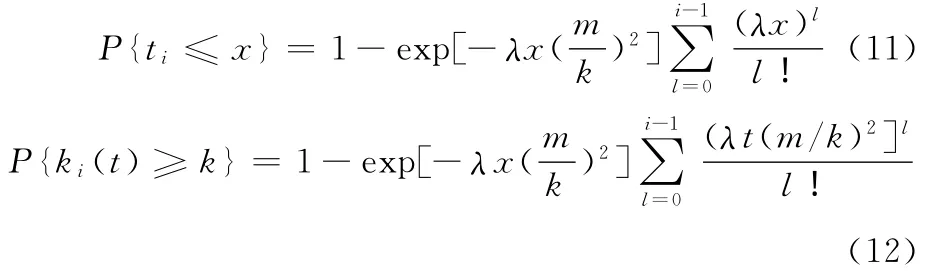
对于充分大的t，当j＞i＞0，k＞m时，有P｛ki（t）≥k｝＞P｛kj（t）≥k｝成立，则证明网络中存在满足上文中定义的中枢节点。

当k≫m时，由式（12）有

因此，网络的稳态平均度分布为

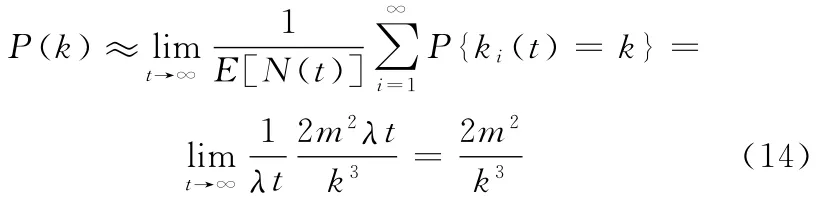
由式（13）、式（14）可知，网络的稳态平均度分布为2m2/k3，说明无标度供应链网络虽然在不断地增长，新的企业节点会不断地融入到某个供应链网络中，但网络通过自适应调节作用，使其平均度分布仍然能达到一个稳定的状态，显示出稳健性。

3.2 增强供应链网络的稳健性

上述内容说明，供应链网络在不断的择优增长过程中对随机失效是具有稳健性的，但同时不能忽略的是，该网络也同样易于受到攻击，只要外部作用在具有较大的度的网络中枢节点上，即攻击供应链网络中的核心企业时，将会导致整个供应链网络出现破坏性的故障，从而导致整个网络瘫痪，因此如何增强网络的稳健性至关重要。下文介绍一种增强供应链网络增长过程中稳健性的方法。

在整个供应链网络的形成过程中，传统的方式是通过改变网络的生长机制，使之在未来的发展中形成小世界网络，以提高整个网络的稳定性。本文在无标度网络遵循的增长、择优连接两种机制基础上，改变择优机制，使之形成一个指数度分布的新网络拓扑结构。具体的网络生产模型如下：

（1）增长。从一个具有m0个节点的网络开始，每次引入一个新的节点，连接到m个已经存在的节点上，这里m≤m0。

（2）优先连接。一个新的节点在t时刻与一个已经存在在网络中的节点i相连的概率

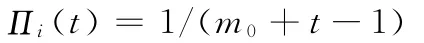
可见，由上述生长机制产生的网络，其节点的连接概率与节点的度完全无关，由概率论知识可知，其平均度分布p（k）＝e1－k/m/m，可见其网络中节点是服从指数分布的，因此可以减弱网络中核心节点的作用。由于核心节点作用的弱化，整个网络就没有较大的攻击点，从而提高了网络的稳定性。

4 应用实例

针对目前汽车行业零部件分布范围广、使用数量大等特点，以浙江省的汽车零部件企业集群为对象来构建供应链网络，以使整车制造企业能更好地管理汽车零部件供应商。在考虑各因素的影响下，以MATLAB为开发工具，主要通过对节点的度的分布、随机点及边的生成情况等方面的研究，直观地仿真出汽车摩托车配件行业供应商的网络分布图，并通过网络中各节点的度的分布情况展现该供应链网络的中枢节点，最后通过网络稳健性的检验，清晰地查看网络中节点的分布是否存在异常情况。

现以从中国青年汽车集团采购部获取的102个汽车零部件供应商的信息为例，假设该供应链网络的增长特征如下：供应链初始节点数m0＝20；每次引入新节点时，新生成的边数m＝5；增长后的网络中节点的总数N＝102；初始网络时，m0个节点均是孤立的。

4.1 网络的度分析

通过以上模式的增长后，运用MATLAB编程对每节点的度、分布情况进行统计和分析，最后输出的各个节点的度的分布和概率如图5所示。

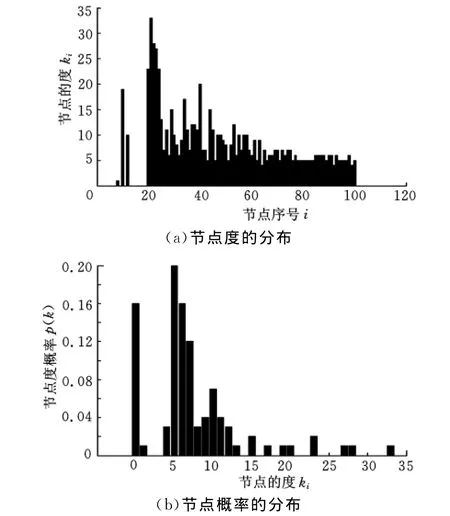
图5 节点的度和概率的分布图

图5中，度为5的节点有17个，度为6的节点有14个，度为7的节点有10个，而度为27、28、33的节点各有1个，度为0的节点有10个。可看出该网络中只有少数的节点具有很高的度，如节点21、22、23，满足P｛ki（t）≥k｝＞P｛kj（t）≥k｝的条件，成为该供应链网络的中枢节点。

4.2 网络的稳健性分析

前面的数据可证明，该供应链网络中绝大多数节点都只有很少的连接，符合无标度网络的特性。通过图5中每个节点的度的分析，对整个供应链网络中节点的度的分布进行MSA分析，得到图6所示的结果。从图6可以看出，有几个节点已明显超出了平均值水平，因此，如果对这些超过控制上限范围的节点企业进行破坏，整个汽车零部件供应链网络将会产生破坏性的伤害。

图6 MSA稳健性分析图

这说明该供应链网络在不断的增长过程中，虽然对一般的随机错误具有很强的免疫力，但是要想始终保持该网络的稳定性，不可避免地需要对该供应链网络中的中枢节点进行相应的保护，从而使该随机网络最终显示出稳定的状态。

5 结语

用复杂网络理论来描述复杂供应链网络，具有简单、直观的特点。复杂网络理论是解决复杂供应链网络中拓扑结构构建的一种可行方法，通过对供应链网络中各企业节点参数进行统计，重点分析具有无标度网络特性的供应链网络，从网络质量控制的角度观察无标度供应链网络，从而给出稳健性供应链网络的定义及其定量分析方法，为无标度供应链网络的分析提供较为科学的依据。本文只是将网络质量控制的原理初次引入到复杂供应链网络的管理，这是网络稳健性分析的开端和基础，更多的课题有待更深入的研究，比如在增强供应链网络稳健性的优化方法方面需要定量的描述等工作。对于这些工作，网络质量控制的原理和复杂网络的理论是一种较为实际并且有效的研究方法。

［1］汪小帆，李翔，陈关荣.复杂网络理论及其运用［M］.北京：清华大学出版社，2006.

［2］胡一肱，朱冰心.复杂网络理论在供应链管理中的应用［J］.物流科技，2007（9）：101－108.

［3］Kinder T.Go with the Flow－A Conceptual Framework for Supply Relations in the Era of the Extended Enterprise［J］.Research Policy，2003，32（3）：503－523.

［4］Thomas M U.Supply Chain Reliability for Contingency Operation［C］//Proceeding of Annual Reliability and Maintainability Symposium.Washington D C，2002：61－67.

［5］郭进利.供应链型网络中双幂律分布模型［J］.物理学报，2006，55（8）：3916－3920.

［6］Santoso T，Ahmed S，Goetschalckx M，et al.A Stochastic Programming Approach for Supply Chain Network Design under Uncertainty［J］.European Journal of Operational Research，2005，167（1）：96－115.

［7］Snyder L M，Scaparra M P，Daskin M S，et al.Planning for Disruptions in Supply Chain Networks［M ］//Tutorials in Operations Research.INFORMS，Hanover，MD，USA：2005.

［8］樊蓓蓓，祁国宁.基于复杂网络的产品簇结构建模及模块分析方法［J］.机械工程学报，2007，43（3）：187－192.

［9］白少布，薛恒新.随机需求下树形供应链网络库存控制策略研究［J］.中国机械工程，2006，17（22）：2338－2341.

［10］Albert R，Barabas A L.Statistical Mechanics of Complex Networks［J］.Reviews of Modern Physics，2002，74：47－97.

［11］郭进利，王翠萍.从网络质量控制角度观察无标度网络［J］.上海理工大学学报，2007，29（1）：22－25.

［12］张根宝.现代质量工程［M］.北京：机械工业出版社，2007.