永磁轴承最小悬浮转速与转动惯量的关系研究

许自豪 钱坤喜 王 颢

江苏大学，镇江，212013

0 引言

为使人工心脏泵长期工作，不因机械磨损而影响其使用寿命，人工心脏泵一般均采用磁悬浮轴承［1－7］。Earnshaw定理指出：一个处在静磁场中的永磁体不可能在全部自由度上实现稳定平衡［8］。Braunbeck［9］经过理论推导认为，在静电场、静磁场和静力场中，如果相对介电常数ξr和相对导磁率μr都不小于1，要实现磁悬浮是不可能的。受Earnshaw定理和Braunbeck推论的影响［8－10］，纯永磁悬浮被认为是不可能达到稳定平衡的，因此现有的磁悬浮技术主要有电磁磁浮和超导磁浮。超导磁浮技术需要大型冷却装置，装置体积过大，不适合人工心脏这样的微型装置，即无法满足植入性的要求。电磁悬浮技术需要复杂的位置测量和反馈控制装置，增加了装置的体积和质量，且自身能量消耗大，这对提高人工心脏的可植入性、可靠性、改善受者的生活品质都是不利的。

Earnshaw定理和Braunbeck推论都是在静态下推导出的结论，笔者基于陀螺效应理论［11－12］提出了运动系统中永磁悬浮的新理论：旋转体在磁力和非磁力（液体压力、空气浮力等）形成的混合力场中可以达到稳定的悬浮，一旦永磁悬浮达到平衡，利用陀螺效应就可以在只有永磁力单独作用的情况下使永磁悬浮保持稳定［13－15］。

江苏大学生物医学研究所发明了一种新型永磁悬浮轴承［16］并成功应用于人工心脏泵，实现了心脏泵转子的六自由度稳定悬浮，解决了纯永磁悬浮不能实现稳定平衡的难题；同时发现永磁悬浮旋转体存在一个最小临界速度，当转速大于此最小临界速度时旋转体会产生陀螺效应，达到稳定平衡［13－15］。

虽然该新型永磁悬浮轴承已成功应用于心脏泵，但该轴承的悬浮稳定性还不明了，有待进一步研究。本文以该新型永磁悬浮轴承为研究对象，以利用该永磁轴承设计的永磁悬浮透平机为研究载体，通过测量透平机转子的偏心距，分析其磁悬浮性能和稳定性，探索影响永磁悬浮旋转体最小稳定转速的因素，即永磁悬浮旋转体实现稳定平衡的最小转速与转动惯量的关系。

1 材料和方法

1.1 传统永磁悬浮轴承和新型永磁悬浮轴承

传统的永磁轴承（图1）只能实现径向支撑或轴向支撑。若要实现叶轮式心脏泵转子的稳定悬浮，需要设计出能同时在径向和轴向产生永磁回复力的磁悬浮轴承，即该轴承需要同时实现径向支撑和轴向支撑。

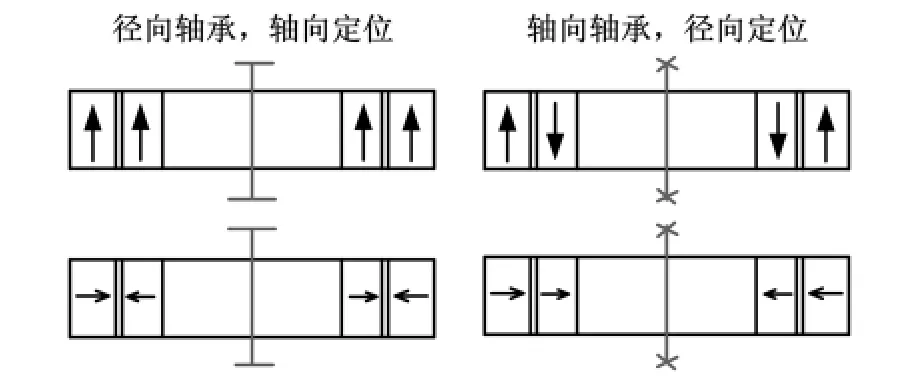
图1 传统的径向永磁轴承和轴向永磁轴承

图2所示为江苏大学生物医学工程研究所研制的一种新型永磁悬浮轴承［11］。小磁环3和大磁环5同心排列，充磁方向相同，但是直径大小不同。在2个磁环中间，有3个磁场区域：A、B、C。在A域和C域，磁力相斥；在B域，磁力相吸。在磁力的作用下，2个磁环保持一定的距离，实现推力和拉力的平衡。如果两磁环相对距离发生变化，将产生一个回复力。回复力的轴向分量相当于磁力弹簧，径向分量相当于径向轴承。利用该新型永磁轴承设计了一种永磁悬浮透平机，本文对该永磁轴承的悬浮稳定性进行深入研究。

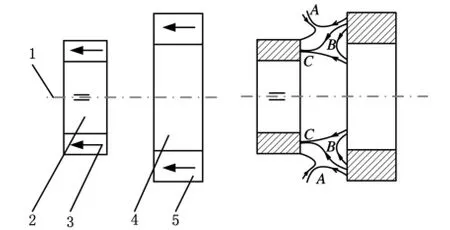
图2 新型永磁轴承

1.2 新型永磁悬浮透平机模型

笔者设计的透平机模型结构如图3所示：同一定子中可安装3个结构和尺寸相同但转动惯量不同的转子。

图3 永磁悬浮轴承透平机结构示意图

现在结合图3详细说明永磁悬浮透平机的结构及工作原理。叶轮3与环形永磁磁钢5、7和9被安装在转子上，环形永磁磁钢4、6、8、10被安装在定子上。永磁磁环4与5、9与10大小相等，同轴同向排列，互相吸引（吸引力互相平衡或抵消）。永磁环6、7、8可等效为两组新型永磁轴承，每一组均可同时起到轴向轴承和径向轴承的作用。永磁环4、5、9、10可增加透平机磁悬浮结构的稳定性。静止时，转子会倾斜，与定子产生径向接触；当转子旋转并达到一定转速时，转子将会产生一种陀螺效应，使得自身开始脱离定子并达到完全悬浮的状态，从而实现稳定的永磁悬浮。按照图3所示永磁悬浮透平机模型的结构，制作了实物模型（图4）。

图4 永磁悬浮透平机模型整体图

图4为永磁悬浮透平机模型的整体图，上部有叶轮，可利用高压空气吹动其旋转。高压气流推动叶轮旋转，从而带动整个转子旋转。当转子达到一定的转速时，从设计上来讲，转子就可以与定子脱离，实现6个自由度的稳定悬浮。

由图5可见，两侧定子和转子上各装有一套磁环，左边的盖板可旋入右边的基座。3个转子的结构和尺寸相同，但转动惯量各不相同，衬底材料分别选用有机玻璃、铝和不锈钢。工作前，透平机模型的转子四周都涂有润滑油，以防止转子转速过慢未能悬浮时，与定子因接触产生的磨损而损坏整个模型。

图5 永磁悬浮透平机模型的定子和转子

1.3 透平机转子转动惯量测量装置

因透平机转子本身由不同材料组装而成，所以无法通过计算得到其转动惯量，只能通过测量得到。3个转子的转动惯量由图6所示的装置测量。

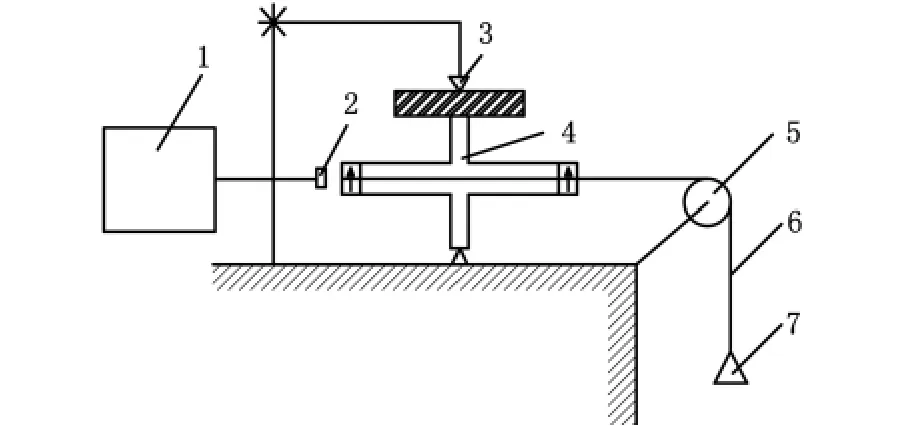
图6 转动惯量测量平台

该装置包括转子固定底座、滑轮、砝码、霍尔传感器和信号处理装置，其测量原理为：细绳绕在转子上，砝码由静止自由下落，通过细绳带动转子加速转动。转子上固定有永磁环，转子转动过程中产生的磁场变化会引起旁边的霍尔传感器输出电压发生周期性变化——转子旋转一周，输出电压变化一个周期，利用信号处理装置检测传感器输出电压，并由输出电压曲线计算出转子的转动惯量。

1.4 透平机转子偏心距测量方法

1.4.1 转子偏心距计算模型

因为透平机定子上的永磁磁环与传感器的相对位置固定，霍尔传感器均匀分布在定子四周（图7）。旋转时，转子中心位置的不断变化使得转子上的磁环在传感器的位置所产生的磁场大小发生变化，进而引起霍尔传感器的输出电压发生变化。因此，可以根据传感器输出电压的变化判断转子中心位置的变化。试验中采用线性霍尔传感器UGN3503U提取转子位置信号。建立透平机转子中心到传感器的距离与霍尔传感器输出电压关系的数学模型，在此基础上建立转子偏心距的数学计算模型。

图7 霍尔传感器在透平机定子上的分布

（1）传感器输出电压与转子中心到传感器距离的关系。图8中，O为定子和传感器运动轨迹的圆心，A为转子的圆心，B为传感器所处的初始位置，C为传感器运动到的位置，∠BOC＝α为传感器绕轨迹中心运动的角度，D为BC中点；定子内半径R＝40.50mm，转子半径r＝40.00mm，传感器 运 动 轨 迹 半 径R＋c＝44.85mm，c＝4.35mm。

图8 转子中心到传感器距离的计算模型

用χ表示转子中心到传感器的距离，则

令α以10°为间隔，从0°递增到180°，即当传感器分别转过上述角度时，记录传感器的输出电压，共得到19个采样点，并绘制成散点曲线图（图9）。

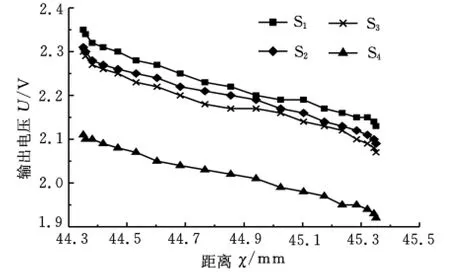
图9 输出电压U与距离χ的关系

从图9可以看出，传感器输出电压U与转子中心到传感器的距离χ之间近似呈现线性关系，利用一元线性回归分析方法，找出二者之间的线性关系，所得回归方程为

（2）转子偏心距模型的建立。图10是偏心距测量的模型示意图，O1为定子和4个传感器所在圆周的圆心，O2为转子的中心；S1、S2、S3、S4为径向均匀分布的霍尔传感器。点H1、H2是由转子中心O2分别向AC、BD作的垂线与AC、BD的交点。

图10 偏心距测量模型

令4个霍尔传感器S1、S2、S3、S4的输出电压分别为U1、U2、U3、U4；用χ1、χ2、χ3、χ4分别表示转子中心到S1、S2、S3、S4的距离，则

由式（2）可得偏心距计算公式：

1.4.2 转子偏心距测量系统

图11所示为永磁悬浮透平机转子偏心距的测量系统。利用此测量系统，对透平机模型转动时转子的偏心距和转速进行测量。

图11 偏心距测量系统

图12为整个测量系统的方框图。4个霍尔传感器和速度传感器被均匀地固定在透平机模型侧面上，传感器电压输出端与偏心距检测装置相连。偏心距检测装置由稳压电源供电。转子顶部固定有叶轮。首先，利用空气压缩机产生高压气流吹动叶轮旋转，使转子达到相当高的转速，然后撤掉高压气流，同时检测装置开始记录转动速度和4个霍尔传感器的电压。在无外界任何干扰的情况下，转子转速因空气阻力缓慢下降，转速较低时检测装置停止记录数据，并把已记录数据通过RS232串行接口上传至计算机中。计算机接受并保存这些数据以便进行下一步的处理。

图12 偏心距测量系统步骤示意图

偏心距检测装置每4ms检测一组数据，一组数据包括4个霍尔传感器的电压值和测量转速的脉冲数。

2 实验数据及结果分析

本次实验中，透平机模型转子外半径r＝40.00mm，定子内半径R＝40.50mm，最大偏心距R－r＝0.50mm。只要转子偏心距达到或接近最大偏心距时，就认为转子未能完全悬浮，与定子有接触；反之，如果偏心距小于最大偏心距且保持一定的距离，那么就可以认为转子与定子无接触，实现了稳定悬浮。悬浮和未悬浮的分界点所对应的转速即为最小悬浮转速。

为分析转子最小悬浮转速，需建立转速与此转速时的最大偏心距之间的关系。转速由转速传感器测出，因为转速是不断在变化的，所以测出的转速实际上是一段时间内的平均转速，再通过上述偏心距计算结果找出此时间段内的最大偏心距，并将所得数据利用软件Origin绘制成散点曲线图。

图13 转子A转速与最大偏心距随时间变化的关系图

由图13可以清楚地看到，由于空气阻力的影响，转子的速度随时间不断下降。当时间在0～1s时，转子速度一直大于4597r/min，最大偏心距稳定徘徊在0.44mm左右，小于0.50mm，此时可以认为转子达到悬浮状态，与定子没有接触。1s之后，转子最大偏心距达到0.50mm，认为转子与定子有接触，未能达到悬浮。因此，这个转子实现稳定悬浮的最小悬浮转速便是4597r/min。

由图14得出，当时间小于0.75s时，转子转速大于3030r/min，转子偏心距一直在0.36mm附 近，明 显 小 于 0.50mm。当 转 速 低 于3030r/min时，转子的偏心距达到0.50mm，说明转子与定子有接触。因此，认为在转速在3030r/min以上，转子就能悬浮。转子B的最小悬浮转速大约为3030r/min。

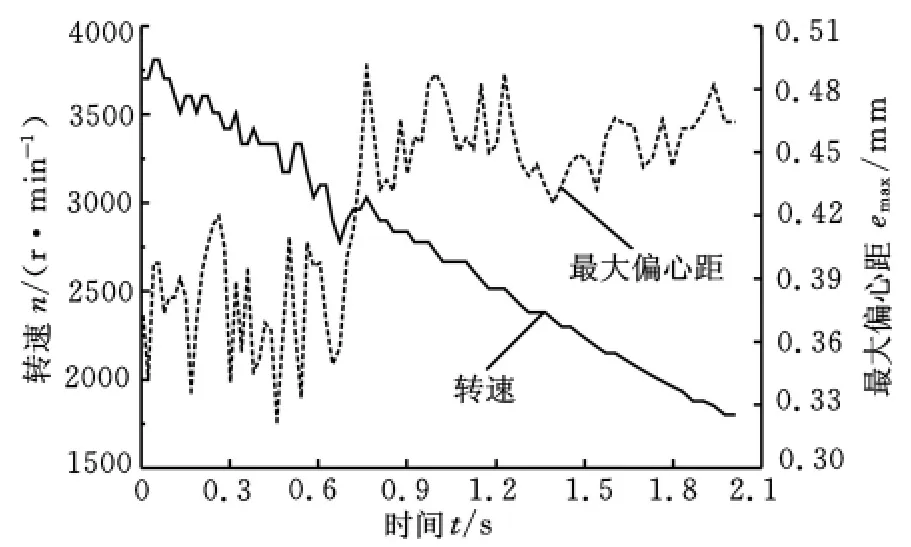
图14 转子B转速与最大偏心距随时间变化的关系图

由图15得出，当时间小于1.25s时，转子转速一直大于2222r/min，转子偏心距在0.40mm附近，明显小于0.50mm。当转速低于2222r/min时，转子的偏心距将近0.50mm，说明转子与定子有接触。因此，认为在转速在2222r/min以上，转子就能悬浮。转子C的最小悬浮转速大约在2222r/min。

图15 转子C转速与最大偏心距随时间变化的关系图

由转动惯量测量装置测得转子A、B、C的转动 惯 量 分 别 为6.293×10－5kg· m2、1.074×10－4kg·m2、2.081×10－4kg·m2。根据以上3个转子转速与最大偏心距随时间变化的关系图，以转子转动惯量为横坐标，对应的转子最小悬浮转速为纵坐标，可得最小悬浮转速与转子转动惯量的关系曲线图（图16）。

图16 转动惯量与最小悬浮转速关系曲线图

由图16可以明显地看出，永磁悬浮轴承转子的最小悬浮转速与转子转动惯量负相关，即随着转动惯量的增大，转子稳定悬浮需要的最小转速减小。这与陀螺玩具具有类似的道理：对于尺寸相同的陀螺来说，密度大的材料制作的陀螺，其转动惯量也大，其保持稳定旋转所需要的转速也较低。这与较重的陀螺更易旋转起来的直观认识是一致的。

3 结语

本文从磁悬浮人工心脏泵入手，基于新的理论设计了新型永磁悬浮轴承，设计了永磁悬浮透平机，并测量了其旋转时的转子偏心距，分析了永磁悬浮轴承转子最小悬浮转速与转子转动惯量的关系。

数据显示，转动惯量分别为6.293×10－5kg·m2、1.074× 10－4kg·m2、2.081× 10－4kg·m2的转子所对应的最小悬浮转速分别为4597r/min、3030r/min、2222r/min。结果表明，同永磁悬浮心脏泵一样，永磁悬浮透平机同样具有陀螺效应，能在一定的转速之上维持稳定的旋转，并且最小临界转速与转动惯量负相关，即转动惯量越大的转子悬浮需要的转速越小。而且，永磁悬浮轴承转子的转动惯量越大，系统稳定所需的最小转速越小，系统的稳定性越好。

［1］刘淑琴，边忠国，李红伟，等.磁悬浮轴承人工心脏泵的研究［J］.中国科技成果，2009（4）：14－16.

［2］Hideo H，Tadahiko S，Setsuo T.Third－generation Blood Pumps with Mechanical Noncontact Magnetic Bearings［J］.Artificial Organs，2006，30（5）：324－338.

［3］刘晓军，刘小英，胡业发，等.人工心脏泵磁悬浮转子质量不平衡及磁耦合研究［J］.中国机械工程，2006，17（16）：1651－1655.

［4］杨晟，刘淑琴，关勇.轴流式磁悬浮人工心脏泵驱动电机的研究［J］.中国机械工程，2010，21（8）：893－896.

［5］Jahanmir S，Hunsberger A Z，Heshmat H，et al.Performance Characterization of a Rotary Centrifugal Left Ventricular Assist Device with Magnetic Suspension［J］.Artificial Organs，2008，32（5）：366－375.

［6］Kataoka H，Kimura Y，Fujita H，et al.Influence of Radial Clearance and Rotor Motion to Hemolysis in a Journal Bearing of a Centrifugal Blood Pump［J］.Artificial Organs，2006，30（11）：841－854.

［7］郭龙辉，张杰民，刘晓程.第三代血泵的研究进展［J］.中国胸心血管外科临床杂志，2010，17（4）：321－325.

［8］Earnshaw S.On the Nature of the Molecular Forces which Regulate the Constitution of the Luminiferous Ether［J］.Trans.Camb.Phil.Soc.，1842，7：97－112.

［9］Braunbeck W.Freischwebende Koerper im Elektrischen und Magnetischen Feld［J］.Z.Phys.，1939，112：764－769.

［10］Geim A K，Simon M D，Boamfa M I，et al.Magnet Levitation at Your Fingertips［J］.Nature，1999，400（6742）：323－323.

［11］Harrigan R M.Levitation Device：U.S.4382245［P］.1983－05－03.

［12］Simon M D，Heflinger L O，Ridgway S L.Spin Stabilized Magnetic Levitation［J］.American Journal of Physics，1997，65：286－292.

［13］Qian K X，Zeng P，Ru W M，et al.New Concepts and New Design of Permanent Maglev Rotary Artificial Heart Blood Pumps［J］.Medical Engineering and Physics，2006，28（4）：383－388.

［14］Qian K X，Wan F K，Ru W M，et al.Study on Stable Equilibrium of Levitated Impeller in Rotary Pump with Passive Magnetic Bearings［J］.Journal of Medical Engineering and Technology，2006，30（2）：78－82.

［15］Qian K X，Xu H X.Gyro－effect and Earnshaw’s Theorem：Stable and Unstable Equilibrium for Rotary and Stationary Permanent Magnetic Levitators［C］//2nd International Conference on Bioinformatics and Biomedical Engineering.Shanghai，2008：1323－1325.

［16］Qian K X.Novel Magnetic Spring and Magnetic Bearing［J］.IEEE Trans.Magnetics，2003，91（1）：559－561.