双金属复合滑动轴承的衬层厚度与温升的关系
邢书明,于冬
(1.北京交通大学 绿色铸锻研究所,北京 100044;2.沈阳铁路信号有限公司,沈阳 110025)
双金属复合滑动轴承(以下简称双金属轴承)与单一金属滑动轴承相比,具有强度高、成本低、使用可靠性高等优点,既能承受高载荷,又具有优异的耐磨性和耐热性[1],故其应用越来越广。相应地,其制造工艺也呈现多样化趋势[2-3]。但是由于双金属轴承存在界面及钢层的导热能力较弱,故其工作过程的温升比单一金属轴承更加值得关注。温度对轴承的摩擦特性影响显著[4],若温度超限可能导致咬合甚至抱死的现象。然而双金属轴承工作过程的传热和温度场研究却十分有限[5-7],至今未见定量计算其温升的数学模型,关于衬层厚度等因素对温升的影响规律的认识仍停留在定性层面。下文根据传热学原理,对双金属轴承工作过程的热行为进行了理论分析,得到了衬层厚度、轴承尺寸和工作条件对轴承温升的影响规律,进一步得到了基于许用温度的衬层尺寸设计计算公式,所得结果可以为双金属轴承设计与制造提供有益参考。
1 衬层温度计算模型
双金属轴承一般由衬层(内层)和钢层(外层)组成,两层之间达到了冶金结合[5,8]。轴承工作时,衬层与轴之间因摩擦而生热,热量通过轴承外壁传出。在工作初期,轴承温度会不断变化,属于不稳定态传热;当工作一定时间后,摩擦生热与轴承的散热之间建立起了平衡,轴承的温度场不再随时间变化,这时属于稳定态传热。若忽略轴承的端部效应,则轴承的传热系统可以看作是双层圆筒壁径向的一维传热。鉴于轴承工作过程的温度变化范围有限,可以认为热物理参数为常数。当达到热平衡时,轴承的温度分布如图1所示。图中t为温度;t0为环境温度;t1,t2,t3分别为对应的轴承内壁、衬层与钢层交界面以及轴承外表面的温度;q为热流密度;r为半径;r1,r2,r3分别为双金属轴承的内半径、界面处半径和外半径;R1,R2,R3分别为衬层、钢层和外表面的热阻;Ф1,Ф2,Ф3分别为通过衬层、钢层和外表面的单位时间的热量(简称热通量)。假定轴承内部为传导传热,双层金属分界面处结合良好,忽略其界面热阻,轴承外表面与环境之间为对流换热,换热系数为h∑,衬层和钢层的导热系数分别为λ1和λ2。根据Fourier定律[9],长度为l的双金属轴承的衬层、钢层及外表面的温度差分别表示为
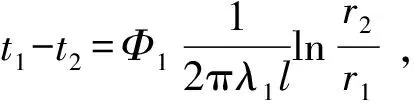
(1)
(2)

(3)

Ⅰ:衬层;Ⅱ:钢层
当传热达到平衡时,流过每个串联热阻的热通量相等,记为Ф,即 Ф1=Ф2=Ф3=Ф,联立(1)~(3)式并整理可得轴承内壁温度的表达式为

(4)
令轴承工作过程的最大温升Δt=t1-t0,于是(4)式可以变为

(5)
轴承在使用过程中的热量来源于轴承与轴之间的摩擦热,虽然轴承与轴之间有润滑膜,但鉴于润滑膜很薄,且没有显著的流动,所以双金属轴承衬层内表面可看作是恒定热流密度的传热。设单位时间单位摩擦面积摩擦产生的热量为Q(J·s-1·m-2),轴承所受的径向平均压强为p(MPa),径向等效承载面积为2πr1l,于是径向压力F=2πr1lp(N),轴承与轴之间的摩擦系数为f,则轴承所受的摩擦力为Ff=2πr1lpf。设轴承工作时轴的旋转线速度为V(m/s),单位时间的摩擦热等于摩擦力与运动速度的乘积,即
Q=2πr1lpfV。
(6)
另一方面,忽略其他无功损耗,则热平衡时有
Q=Φ=2πr1lpfV。
(7)
将(7)式代入(5)式,并令衬层厚度为δ1,即r2=r1+δ1,化简整理得
(8)
令

K值的大小反映了轴承的结构尺寸r1,r2,r3和传热能力(各层的热导率λ1和λ2以及外边界的散热条件h∑)对温升的影响程度,不妨将系数K称为双金属轴承的热结构因子。于是(8)式简化为
Δt=KpfV。
(10)
由(10)式可见,轴承的温升受工作条件p,f以及热结构系数制约。在轴承热结构一定的前提下(即K值不变),双金属轴承工作过程的温升随径向载荷和摩擦系数呈线性规律增大。因此强化轴承与轴之间的润滑,减小衬层与轴间的摩擦系数,对于降低温升具有重要的实际意义。
2 热结构因子及其影响因素
由(10)式可见,热结构因子K值越大,在相同载荷和润滑条件下的温升倾向越大,所以K值的大小反映了轴承温升的敏感程度,有必要深入研究K值的影响。
在一定的工作条件下,轴承的内径r1受轴径控制,而其外径、衬层厚度以及衬层材料是3个主要的可变因素,为此用(9)式分别对衬层导热系数λ1、衬层厚度δ1及外径r3求偏导数,得
(11)
(12)
(13)
(11)式恒为负值,说明K随衬层导热系数λ1的增大而减小,即K是衬层导热系数λ1的非线性减函数。为了降低轴承温升,要尽量提高衬层材料的导热系数。(12)式的符号随衬层与钢层导热系数的相对大小而变化。当λ1>λ2时为负值,即衬层材料导热系数大于钢的导热系数时,K随衬层厚度的增大而减小,K是衬层厚度δ1的非线性减函数;当λ1<λ2时为正值,即衬层材料导热系数小于钢的导热系数时,K随衬层厚度的增大而增大,K是衬层厚度δ1的非线性增函数。只有双金属轴承衬层材料的导热系数大于钢的导热系数时,增大衬层厚度才有意义。(13)式则恒为正值,即增大轴承外径r3(相当于增大轴承厚度)将使滑动轴承的热结构系数K增大,温升敏感性增大。因此在满足力学性能要求的前提下,轴承厚度越小越有利于降低温升。
3 基于许用温度的衬层厚度设计
实际上,对于给定的衬层材料制成的双层轴承,一般都有一个许用温度或许用温升。常见衬层材料的许用温度为140~280 ℃[10]。设衬层许用温度为tc,对应许用温升为ΔTc=tc-t0,用tc代替(8)式中的t1或用ΔTc代替(8)式中的t1-t0,并加以整理即可得到对应于一定的许用温度,或许用温升条件下的衬层最小厚度δ1的计算式,即
(14)
或
(15)
可见,只要知道了许用温度(或许用温升)、内径、外径和材料的导热系数,即可根据(14)或(15)式计算出衬层厚度。该衬层厚度就是对应于许用温度的临界厚度。
为了说明此临界厚度是最大厚度还是最小厚度,用(14)式对许用温度或许用温升求偏导数,得
(16)

(17)
可见,当衬层导热系数大于钢背导热系数(λ1>λ2)时,该偏导数值小于零,衬层厚度是许用温度的减函数,这时随着许用温度的提高可以减小衬层厚度,(14)或(15)式给出的是衬层厚度的最小值。为了确保实际温升小于许用值,必须使衬层厚度大于(14)或(15)式计算的厚度,即这时的临界衬层厚度是最小厚度。
但是当衬层的导热系数小于钢背的导热系数(λ1<λ2)时,该偏导数值大于零,衬层厚度是许用温度的增函数,这时随着许用温度的提高可以增加衬层厚度,(14)或(15)式给出的是衬层厚度的最大值。为了确保实际温升小于许用值,必须使衬层厚度小于(14)或(15)式计算的厚度,即这时的临界衬层厚度是最大厚度。这说明双金属轴承的衬层厚度并不是越大越好。
4 结论
(1)双金属轴承工作过程的温升是功率、径向载荷和摩擦系数的线性增函数,其比例系数反映了双金属轴承结构和材料传热特性对轴承温升的综合影响作用。热结构因子越大,滑动轴承越容易温度超限。
(2)双金属轴承的热结构因子K是衬层导热系数λ1的非线性减函数,是衬层厚度δ1的非线性减函数(当λ1>λ2时)或非线性增函数(当λ1<λ2时)。
(3)双金属轴承的衬层厚度存在临界值。当衬层导热系数大于钢背导热系数(λ1>λ2)时,临界厚度是确保温升不超限的最小衬层厚度;当衬层导热系数小于钢背导热系数(λ1<λ2)时,临界厚度是确保温升不超限的最大衬层厚度。

