汽车等速万向节传动轴的可靠性设计与解析
石宝枢
(比亚迪汽车有限公司 传动轴总厂,广东 深圳 518118)
符号说明
d——轴的直径,mm

Dw——钢球直径,mm
F——失效率
G——材料剪切弹性模量,MPa
IP——轴横截面的极惯性矩
k——轴半径的计算系数
n——安全系数
r——轴的半径,mm

R——可靠度
W——轴承受的转矩,N·mm

zR——可靠性系数
σr——轴半径的标准差,mm
σW——传动轴承受的转矩的标准差,N·mm
τ——轴的剪切应力,MPa

στ——轴剪切应力的标准差,MPa
δ——许用剪切应力,MPa

σδ——许用剪切应力的标准差,MPa
α——轴半径的偏差系数
θ——轴单位长度的扭转角,rad
η——传动效率
汽车等速万向节传动轴总成主要的失效模式是传动轴疲劳断裂。其根本原因是在传动轴总成产品设计时:(1)对其载荷和强度的变化未予考虑;(2)对传动轴的可靠度没有进行定性的分析和定量的确定;(3)对传动轴的直径没有进行精确的可靠性设计与计算。
下文将对等速万向节传动轴进行可靠性设计与计算。同时,还就某些参数对传动轴可靠性的影响进行系统、定量地分析。
1 传动轴的转矩及产生的剪切应力
汽车等速万向节传动轴总成为一端固定,另一端承受转矩。
1.1 转矩
转矩与材料剪切弹性模量、扭转角和极惯性矩成正比,其值为[1]
W=GθIP,
(1)
对于实心轴,IP=πd4/32。
汽车等速万向节传动轴总成的固定端一般为球笼式万向节,该万向节内部基本属于静态运转工况。在该工况下,钢球与星形套和钟形壳之间均为共轭Hertz接触。显然,星形套、钟形壳和钢球主要承受接触应力[2]。根据Hertz接触理论的分析和应力的计算,汽车传动轴的额定转矩为[3]
(2)
考虑到可靠性,对传动轴必须给定足够的安全系数n,一般n=1.8~2.0,若传动轴总成的传动效率为η,则其平均转矩(即计算转矩)为
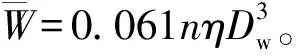
(3)
1.2 剪切应力
在W的作用下,传动轴产生的剪切应力为
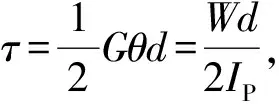
(4)
对于实心轴,
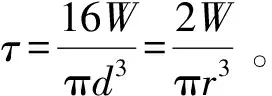
(5)
轴产生的剪切应力的平均值为
(6)
1.3 剪切应力的标准差
由于τ=2W/πr3,τ亦符合正态分布,根据2个正态分布函数之比,将新的概率密度函数一部分在均值处展开为Taylor级数,略去其高次项,取其线性项,可得出传动轴剪切应力的方差为[4]
(7)
则,标准差为
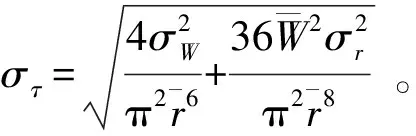
(8)
2 传动轴的可靠性设计
根据上述已知条件,可对汽车等速万向节传动轴进行如下的可靠性设计。由于载荷、强度、结构尺寸、工况等均具有变化性和统计本质,因此通过概率密度函数来进行研究。
当轴的剪切应力τ和许用剪切应力δ均是正态分布时,其概率密度函数分别为[5]
(9)
(10)
由于可靠度是指许用剪切应力超过实际剪切应力(即δ>τ)的概率,如令y=δ-τ,则f(y)为
(11)
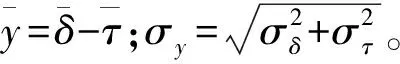
可靠度R为y>0的概率,即
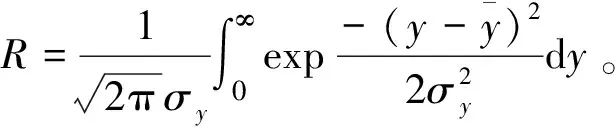
(12)
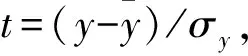
(13)
由于标准正态分布函数为偶函数,所以,(13)式可变为
(14)
(15)
联立上述方程组即可求解。
3 设计实例
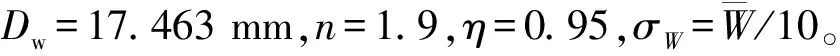
按R=0.999,查标准正态分布表得可靠性系数zR=3.091。
将有关的已知参数代入(6)式和(8)式,得剪切应力的平均值和标准差分别为
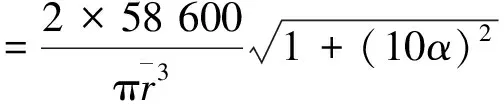
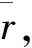
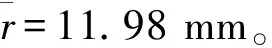
此产品小批试制后,随机抽取10个传动轴总成样品,分别进行静扭强度试验、20万次扭转疲劳试验、可靠性和耐久性试验以及50 000 km高速和强化道路试验,样品均完好无损。这表明,无论在理论还是实践上,上述设计结果不仅能够满足规定的可靠性要求,而且是优化设计的最佳值。
4 各参数对传动轴可靠度的影响
基于上述实例,研究轴半径偏差、许用剪切应力标准差、轴平均半径对传动轴可靠度的影响。
4.1 轴半径偏差的变化对可靠度的影响
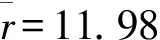

(16)
现改变半径偏差系数α值,计算相应的zR值及R,以分析传动轴半径偏差的变化对其可靠度的影响。R随α的变化曲线如图1所示。
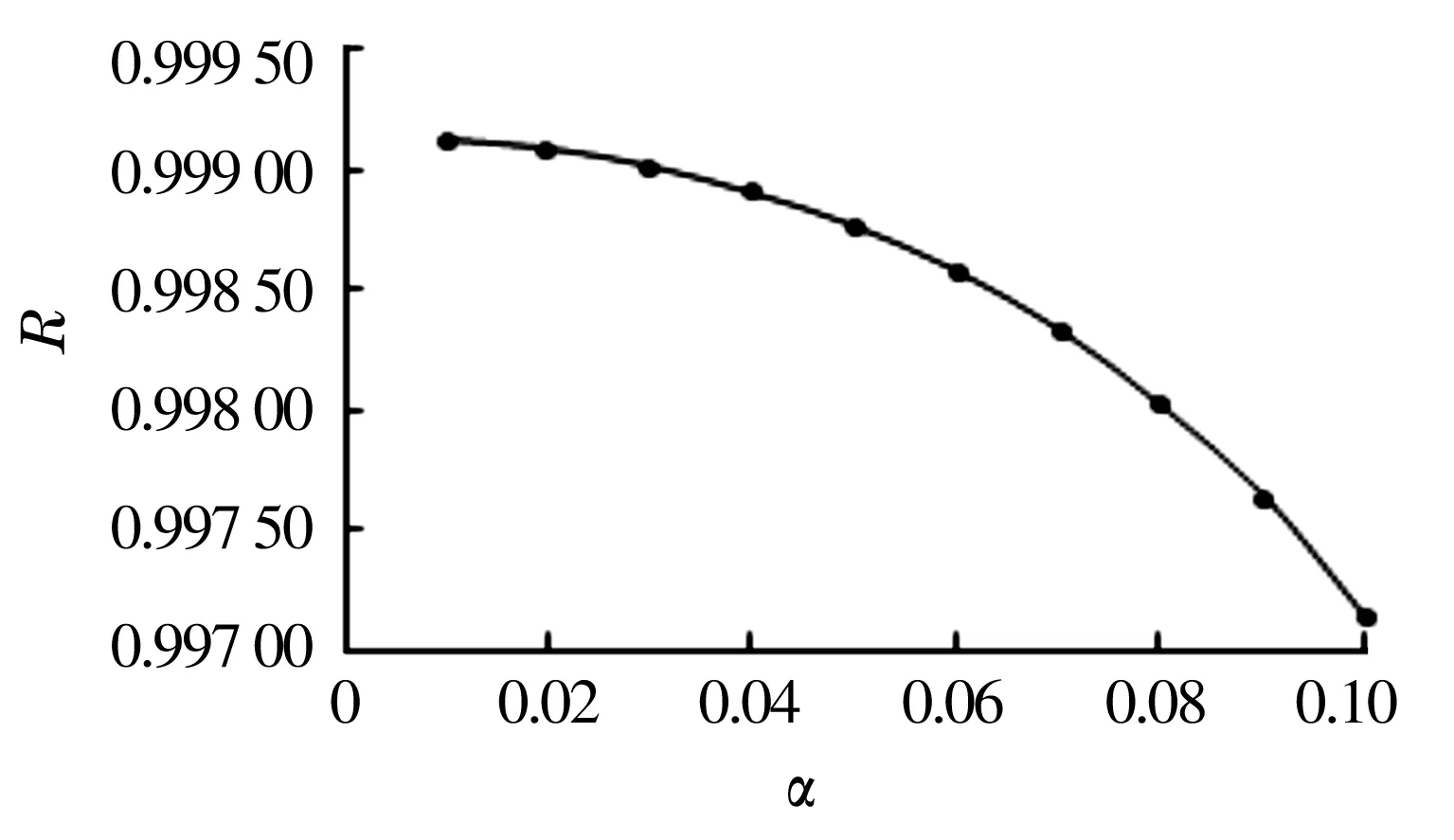
图1 可靠度随半径偏差的变化曲线
由图1 可以看出,可靠度R随传动轴半径偏差系数α的增大而减小。因此,减小传动轴半径的偏差,或者提高该尺寸的公差等级和稳定性,可确保传动轴具有较高的可靠度。
4.2 许用剪切应力标准差变化对可靠度的影响
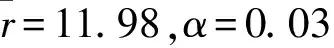
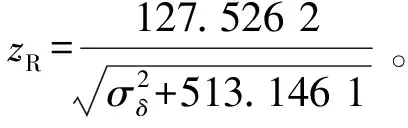
(17)
现改变σδ值,计算相应的zR值及可靠度R,以分析许用剪切应力标准差的变化对传动轴可靠度的影响。R随σδ的变化曲线如图2所示。
由图2可以看出,传动轴可靠度R随σδ的增大而减小,所以尽可能保持载荷和工况的稳定,亦是提高传动轴可靠性的关键。
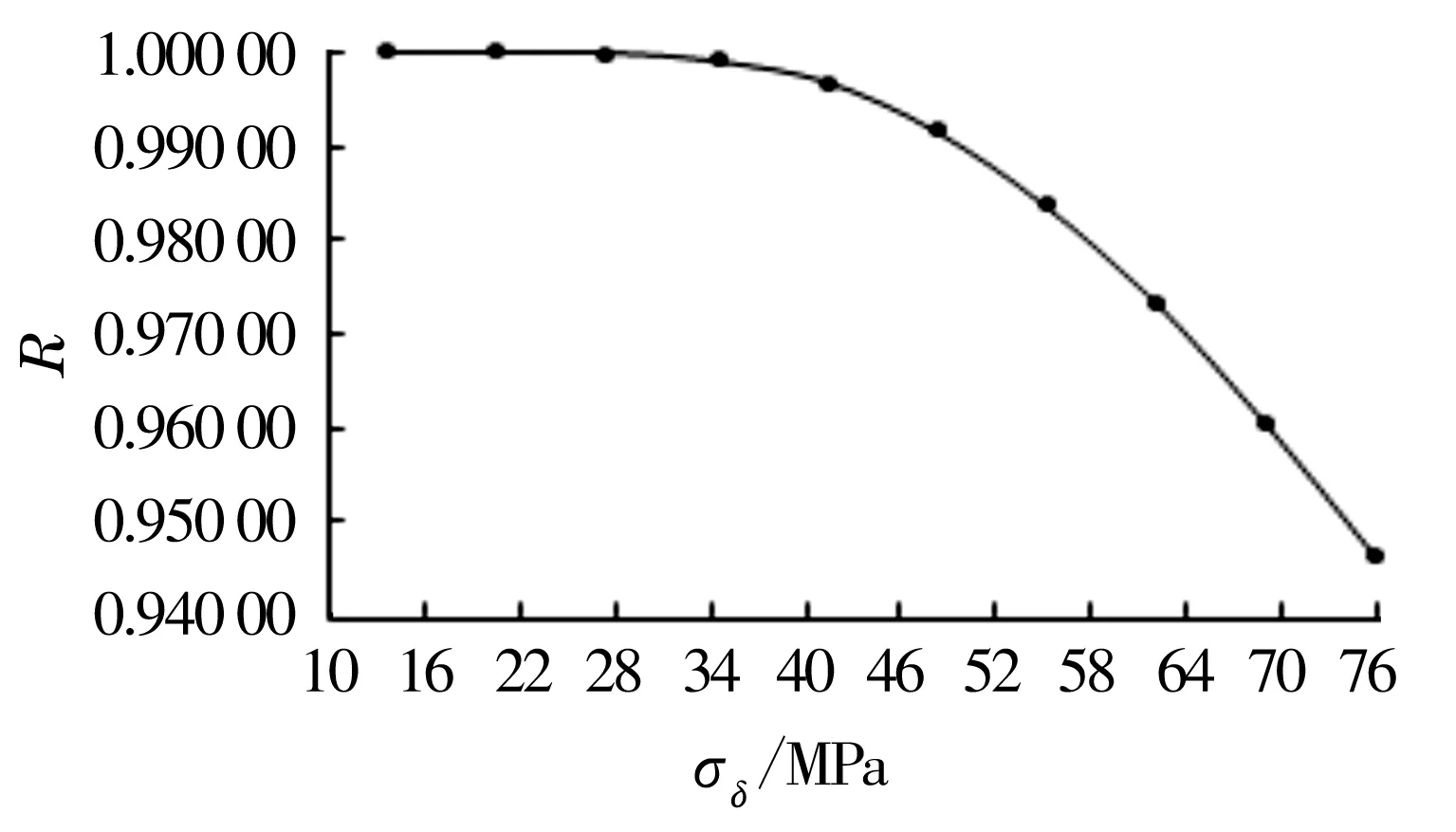
图2 可靠度随许用剪切应力标准差的变化曲线
4.3 轴平均半径的变化对可靠度的影响
将α=0.03,σδ=34.45代入(6),(8)和(15)式组成的方程组得
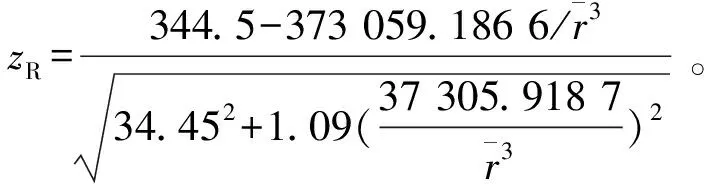
(18)
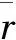
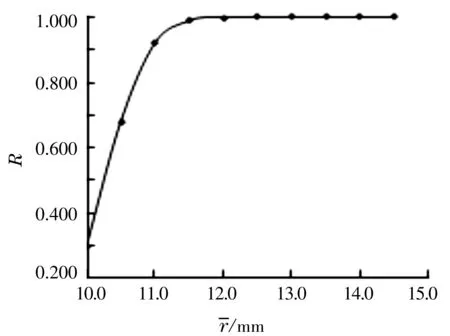
图3 可靠度随平均半径的变化曲线
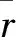
5 结束语
在汽车等速万向节传动轴的可靠性设计中,传动轴的许用剪切应力及尺寸等基本参数不变,而这些参数的标准差均增大,传动轴的可靠度将迅速下降。因此,当传动轴许用剪切应力及尺寸等参数平均值不变时,严格控制其分散性,是保证传动轴可靠性的重要措施之一。

