平稳小波变换在轴承振动信号去噪中的应用
隋文涛,张丹
(山东理工大学 a.精密制造与特种加工省级重点实验室;b. 电气与电子工程学院,山东 淄博 255049)
许多机械是在非平稳状态下工作,采集的振动信号往往受到噪声信号干扰。研究机械振动信号的滤波消噪,对机械设备的故障诊断有着重要的理论和实践意义[1-4]。
传统的消噪方法是根据信号和噪声的频谱分布规律,采用滤波器进行信号降噪。先采用Fourier变换将含噪信号变换到频域,然后采用低通滤波器进行去噪。但是,当噪声和信号的频带有重叠时,比如信号含有白噪声,低通滤波去噪效果较差。传统的消噪方法的理论基础是Fourier变换,存在保护信号局部特性和抑制噪声之间的矛盾。小波变换具有良好的时频局部化特性,在信号消噪中得到广泛的研究并取得了非常好的应用效果,成为信号去噪的主要方法之一。为了有效提取振动信号中的故障特征,提出利用平稳小波变换进行降噪。先对信号进行平稳小波分解,再利用阈值计算方法确定阈值。试验结果表明,该方法较好地保留了振动信号的边缘特征,为故障特征提取创造了良好的条件。
1 平稳小波变换
在Mallat离散小波变换算法[5]中,信号经过低通和高通滤波器卷积后,进行隔二取一的下采样得到尺度系数和小波系数。但由于进行下采样得到的小波系数缺乏平移不变性。平稳小波变换(stationary wavelet transform,SWT)的引入在一定程度上解决了该问题。平稳小波变换与离散小波变换相同之处在于在每层上都运用高通和低通滤波器对输入信号进行处理,不同之处是平稳小波变换不对输出信号进行下采样,而是进行上采样。
假设s[n]的长度为N,其中N=2J,J为整数。h1[n] 和g1[n] 是由正交小波确定的高通滤波器和低通滤波器。在第1层,输入信号x[n]与h1[n]卷积得到近似小波系数a1[n],与g1[n]卷积得到细节小波系数d1[n]。

(1)
(2)
因为没有进行下采样,故a1[n]和d1[n]的长度都是N,而不同于离散小波变换中的长度N/2。在平稳小波变换的下一个分解层次a1[n]分解成如同前述的两部分,h2[n] 和g2[n]分别为h1[n]和g1[n]通过上采样得到。
aj+1[n]=hj+1[n]*aj[n]
(3)
dj+1[n]=gj+1[n]*aj[n]
(4)
2 根据峭度确定阈值
虽然文献[6]在理论上证明并找到了最优的通用阈值,但在实际应用中效果并不十分理想,而且也未考虑轴承振动信号本身的特点。为更好地提取滚动轴承故障信息,针对以上问题,提出了新阈值,如 (5) 式所示。新阈值是为冲击型的故障信号而提出,考虑到了信号和噪声的小波系数在不同尺度上的特性,对分析机械类振动信号更有针对性,去噪效果更有效。
式中:N表示待分析细节层的小波系数长度;σ为信号中的噪声方差,可以用小波系数估计,
(6)
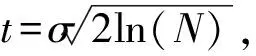
分母中Kurtosis(j)/3主要起到根据峭度[7]调节阈值的作用。Kurtosis(j)=3.0时,信号属于Gauss信号,表明该尺度上有效信号与噪声混杂,不易区分开来。
Kurtosis(j)<3.0时,信号属于亚Gauss信号,表明该尺度上有效信号不占主要成分,为了剔除噪声信号,阈值应增大。
Kurtosis(j)>3.0时,信号属于超Gauss信号,正是机械故障冲击信号的特性,表明该尺度上有效信号占主要成分。直观来看,为了保留冲击信号,阈值应随峭度的增大而减小。
3 试验验证
3.1 仿真验证
根据轴承外圈单个损伤点情况的理论模型,仿真外圈单点损伤故障振动信号。假设损伤引起的振动的固有频率为fn=3 kHz,外圈故障特征频率BPFO=120 Hz,采样频率fs=12 Hz,采样点个数1 024个。
在单纯仿真故障信号上分别再加上信噪比(单位为dB)不同的Gauss白噪声作为待分析的降噪前信号,如图1所示。
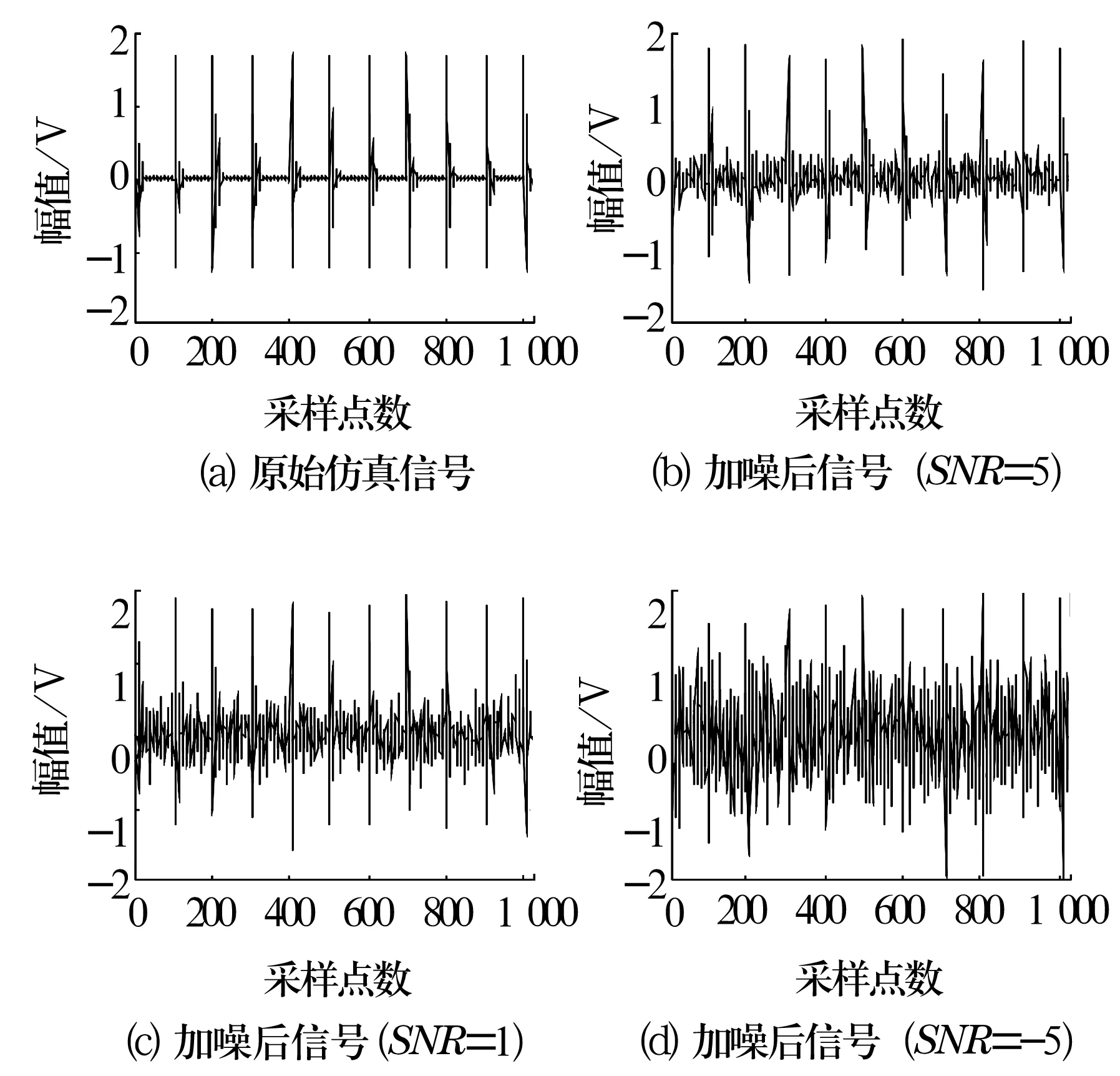
图1 仿真外圈故障信号及其叠加白噪声后的信号
运用改进降噪方法和通用阈值降噪方法对图1b~图1d的信号进行处理,信噪比见表1。可以看出,3种情况下改进方法获得的信号信噪比都较高。
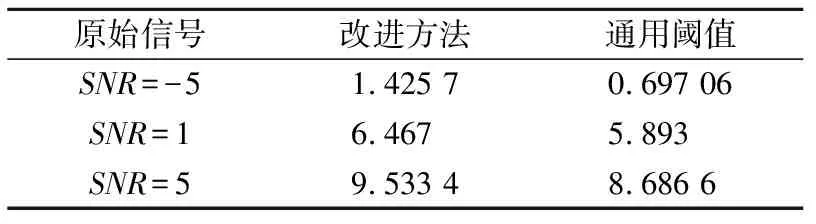
表1 降噪后信号信噪比
3.2 试验数据验证
试验使用SKF公司的深沟球轴承,型号为6205。轴承的内径为25 mm,外径为52 mm,宽度为15 mm。轴承转速1 750 r/min,带动轴承旋转的电动机功率为1.47 kW。该轴承的3个特征频率分别为:滚动体故障频率140 Hz、内圈故障频率160 Hz、外圈故障频率105 Hz。
从图2a可以看出,故障信号非常微弱,基本上被噪声所淹没,时域图无法区分故障模式,直接进行包络分析,诊断效果不是很好。
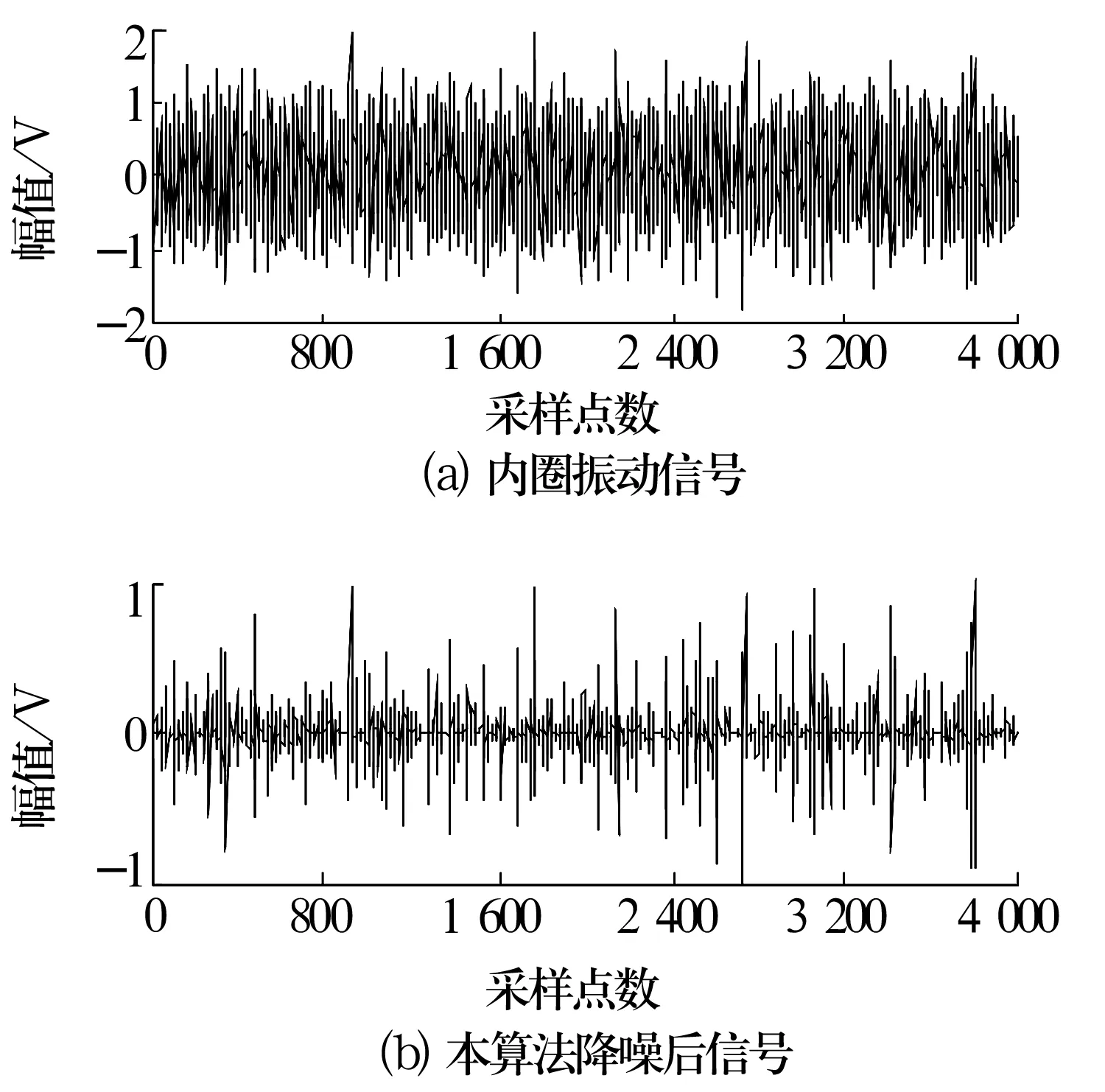
图2 信号降噪前、后对比
对图2a和图2b分别进行包络分析,如图3所示。从图3a无法得到故障信息、而图3b中清楚显示160 Hz和320 Hz处存在峰值,正好对应1倍和2倍的内圈故障特征频率,也就意味着内圈存在缺陷。
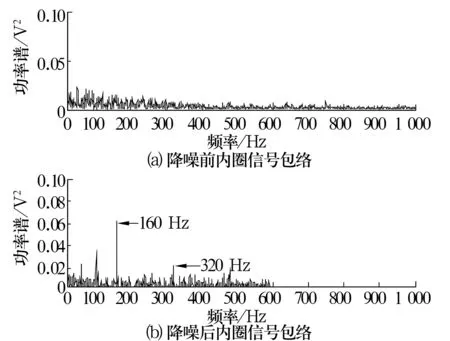
图3 降噪前、后信号包络分析
4 结束语
针对轴承振动信号的特点,提出了基于峭度的阈值消噪方法。该方法可以很好地提高信噪比,有效地提取信号中冲击成分,为正确识别故障特征提供了有力的保证。最后通过仿真试验和轴承振动信号消噪试验说明,文中提出的降噪技术是有效的。

