马氏链点值预测方法和时序分析预测方法的统计试验研究
沈永梅,王 琼,何哲飞
(常州大学 数理学院,江苏 常州 213164)
0 引言
马尔可夫链状态预测方法已经在水资源科学中得到了广泛的应用。张宸、林启太[1]研究了马尔可夫链理论在矿区降水灾害预测中的应用;郑文瑞等[2]研究了马尔可夫链理论在水污染状态风险评价中的应用;张文坚[3]用马氏链预测理论研究了城镇洪涝灾害的分析;宋印胜[4]和王渺林[5]研究了马尔可夫链理论在水位预测中的应用;冯耀龙,韩文秀[6]研究了马尔可夫链在河流丰枯状况预测中的应用。近年来,一些学者开始研究基于马氏链状态预测方法的点值预测方法[7]。本文拟提出一种简单的基于马氏链状态预测方法的点值预测方法,并将其与普遍接受的时间序列分析预测方法进行基于统计试验的比较分析。基于马氏链状态预测方法的点值预测方法的预测结果是通过MATLAB软件实现的,而时间序列分析预测方法的结果是通过DecisionTime软件实现的。
由于我国有关水文计算的规范规定,我国主要河流的径流量和降水量均可假定为服从P-III型分布或三参数对数正态分布。因此本文的主要目的是利用随机模拟技术,生成服从P-III型分布和三参数对数正态分布的相依伪随机数序列,然后再将基于马氏链状态预测方法的点值预测方法与时间序列分析预测方法进行比较分析。研究的主要问题如下:(1)马尔可夫链点值预测方法与时间序列分析预测方法的精度哪个高;(2)对于马尔可夫链的三种点值预测方法,哪种预测方法较优;(3)马尔可夫链点值预测方法对P-III型分布和三参数对数正态分布水文分布具有适应性;(4)序列的变差系数Cv和偏态系数Cs对预测精度的影响。
1 马尔可夫链点值预测方法的思想
马尔可夫链的状态预测方法可见文[6],这里主要说明如何根据区间预测结果来确定点预测值。根据经验可知,下一个时段的指标值与上一个时段的指标值有很大的关系,故本文提出了基于本时段 预测中值与上一时段预测中值的预测方法,这里的预测中值是指预测状态所对应的状态区间的中点。假设状态空间E={1,2,…,m},设各状态区间的中点值分别为M1,M2,…,Mm,通过马尔可夫链的区间预测方法得出本时段的预测状态为s(t),上一时段的状态为s(t-1),则本时段的点预测值为βMs(t-1)+(1-β)Ms(t),其中β为上一时段预测中值在整个点预测值中所占的权重。β的选取一般可采用如下方法:假设通过马氏链状态预测方法所得的上一时段的预测状态为s(t-1),而转移到该状态的概率为Ps(t-1);本时段的预测状态为s(t),转移到该状态的概率为Ps(t),则
基于绝对分布的马尔可夫链预测(ADMCP)方法对应的点值预测方法记为ADMCPP,叠加马尔可夫链预测(SPMCP)方法对应的点值预测方法记为SPMCPP,加权马尔可夫链预测(WMCP)方法对应的点值预测方法记为WMCPP。
2 最优时间序列分析预测方法的确定
时间序列分析预测方法比较多,其中ARIMA模型是其中较为常见也非常重要的一类数据处理和预测的方法。从已有数据序列选择一个好的ARIMA模型需要很多步骤,包括模型的初步识别、定阶、参数估计、模型的检验等,这些都给模型的选择带来了很大的困难。统计试验中所需处理的数据序列很多,不可能进行一一分析,所以需要有一种新的方法来解决这个问题。
本文选用了DecisionTime软件进行数据处理和预测分析,由于数据序列很多,所以选择了专家预测模式(Expert Modeler),DecisionTime软件会根据数据自身的特征选择最适合的模型来拟合和预测数据。所选择的模型除了前面所提到的模型还有如下7种:Simple exponential smoothing、Holt’s exponential smoothing、Brown’s exponential smoothing、Damped exponential smoothing、Seasonal exponential smoothing、Additive Winters’exponential smoothing、Multiplicative Winters’exponential smoothing。其实这些模型都是包含于ARIMA模型中的,也就是说它们都是ARIMA模型的特例,之所以用他们来拟合和预测数据就是在拟合效果差不多的情况下尽量的节省数据的运算和处理的时间,这些模型虽然对长期的预测效果不如ARIMA模型,但是他们对短期预测还是很有效的,而且它们对有线性趋势和季节性的序列能处理得更好。
这里需要说明的是,在专家预测模式下DecisionTime软件给出了最适合你的数据的模型。如果在预测向导中没有你选定的模型,专家预测模式会选择最好的指数平滑(修匀)模型和最好的单变量的ARIMA模型:首先,专家预测模式会选择用最小的标准BIC值确定最适合的指数平滑模型;然后,专家预测模式会判断这组数据是否需要进行变换或者是通过差分使其平稳化,再通过ACF和PACF图像来确定一个初始模型,这个模型是调整过的或者多次调整过的,通过t值和Ljung-Box统计量,以及残差ACF和残差PACF图像;最后专家预测模式会在指数平滑模型和ARIMA模型中选择标准BIC值更小的模型作为预测用模型。本文称通过这种方法得到的最优预测方法为时间序列预测方法,记其为“TSAP”法。
3 试验设计与试验结果的综合分析
3.1 试验设计
3.1.1 伪随机数序列的长度和分布参数的设计
由于天然河流的实测水文资料比较短,一般少于60年,因此只有在小样本下进行预测方法的比较才有意义。出于这种考虑,本文对于生成的序列,仅考虑长度为100的服从P-III型分布和三参数对数正态分布的相依伪随机数序列,分别用马尔可夫链点值预测方法和较优的时间序列预测方法对相同的数据进行预测,并比较两类预测方法的效果。我们分别对两种分布采用了5组总体参数(见表1)共生成了10组长度为80000的数据序列,数据的生成方法见文[8]。
经验表明,大多数实际径流量和降水量资料的参数都在表1的参数值的范围内,由于一般的水文序列均为弱相关序列,所以为了方便起见序列的一阶相关系数统ρx(1)一规定为0.2。
3.1.2 计算方案设计及预测偏差的衡量
按表1中给定的各组参数分别生成5组长度为80000的服从P-III型分布和对数正态分布的相依伪随机数序列,依次取100个数据(分别考虑取50次、200次和800次)。对于每取得的长度为100的相依伪随机数序列,我们可假定前C个数据为实测资料,利用这C年的资料序列,分别运用马尔可夫链点值预测方法和较优的时间序列预测方法预测后100-C年的数据值,并比较两种预测方法的优劣。比较的指标设定如下:可以用生成的数据值与预测值求得绝对预测误差向量,这是一个维数为100-C的向量。假如重复试验N(N=50、200、800)次,则马尔可夫链点值预测方法和较优时间序列分析预测方法都可以得到N个绝对预测误差向量,这些向量的维数均为100-C,如果把这些向量作为行向量排成矩阵,可构成一个N×(100-C)的绝对预测误差矩阵,记为ΕN×(100-C),如果对其列求平均值,则可以得到多次试验下的绝对预测误差的平均向量,它能反映预测方法的准确性,从而反映预测方法的优劣;若对其列求方差,则可以得到在多次试验情况下的绝对预测误差的方差向量,其能反映预测方法的稳健性。如果要对两类方法进行比较,还需找到了一个能反映向量大小的量,本文选用的这个量为向量的各个分量的平均值。
为了更清楚地说明上面一段文字,可用数学符号把相关量表示出来。假设重复试验的次数为N,其中第k(k=1,2,…,N)次所取的100个数据值为,假定前C个实测值记为,后100-C个数据值记为,用两类预测方法得到的预测结果统一记为,则绝对预测误差矩阵为ΕN×(100-C)=(eki),其中eki=|x(k,i)[-x[(k,p;i)|,i=1,2,…,100-C。
绝对预测误差均值向量mvape(mean vector of absolute predicting error)的第i个分量定义为:

用其平均值来衡量预测方法优劣,简记为mmvape(mean of mvape)
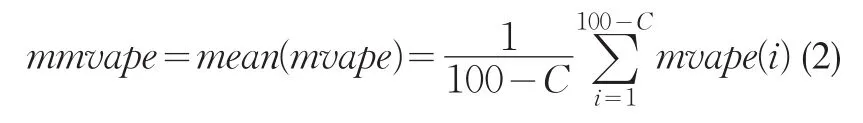
绝对预测误差方差向量vvape(variance vector of absolute predicting error)的第i个分量定义为:
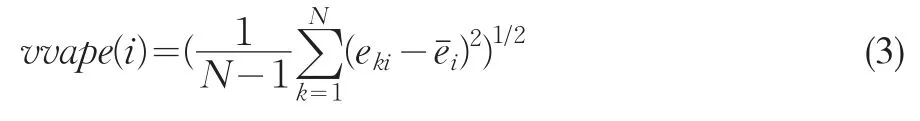
其中

用其均值来衡量预测方法的稳健性,简记为mvvape(mean of vvape)
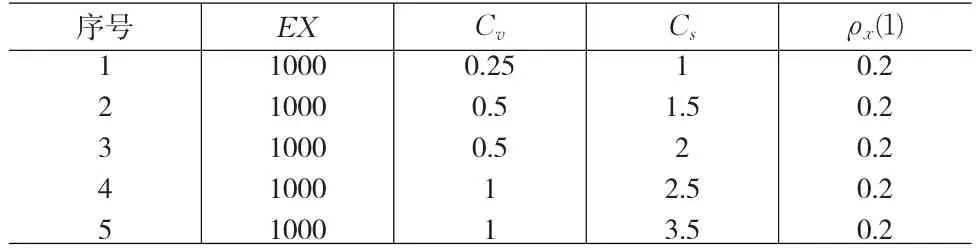
表1 总体参数值表

预测误差分析表中每一种预测方法下面有两列,分别记录了每组数据用该方法时的mmvape和mvvape。每张表格的倒数第二行是关于五组不同参数的数据的mmvape和mvvape平均值,最后一行是以较优的时间序列预测方法所得的预测值为基准,基于马尔可夫链状态预测方法的点值预测方法的相对误差下降率。
3.2 预测结果汇编
3.2.1 对数正态分布数据的两类预测方法的统计试验结果
选定实测资料数据长度C为60,利用这60年的资料序列,分别运用马氏链点值预测方法和较优的时间序列预测方法预测后40年的数据值。马尔可夫链预测方法中选取的状态分级参数α=(α1,α2,α3,α4)如表2。
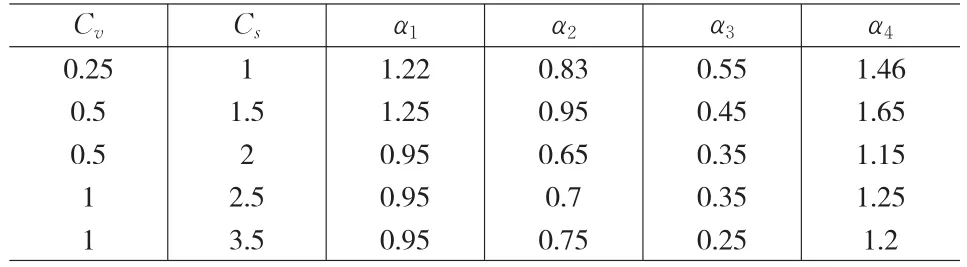
表2 不同参数值所对应的α表
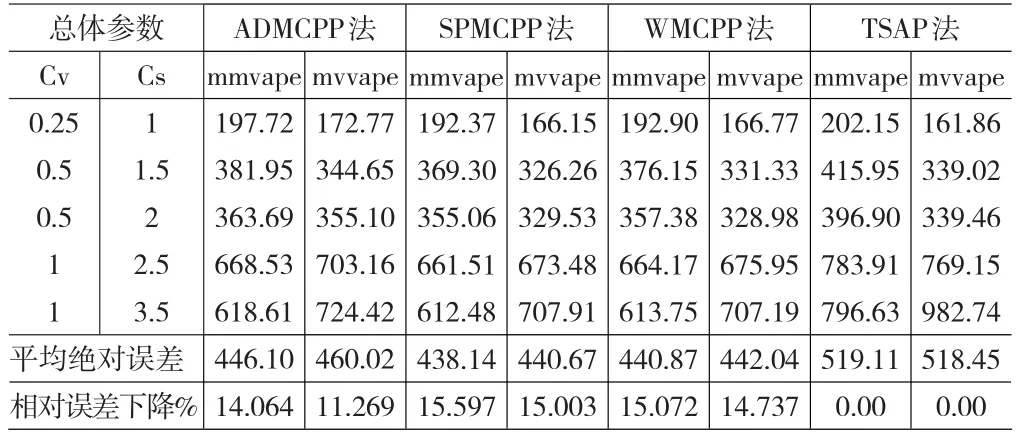
表3 对数正态分布数据的马氏链点值预测方法及较优时间序列预测方法的预测误差分析N=50

N=200

N=800
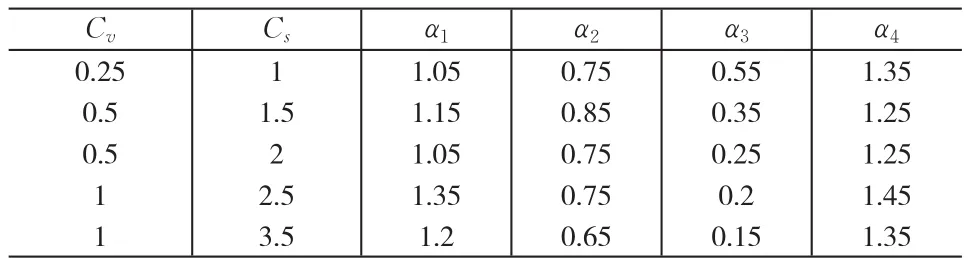
表4 不同参数值所对应的α表

表5 P-Ⅲ型分布数据的马氏链点值预测方法及较优时间序列预测方法的预测误差分析N=50
基于统计试验的预测结果如表3,表3中分别列出了试验次数N取50、200、800次的条件下的预测结果。
3.2.2 P-Ⅲ型分布数据的两类预测方法的统计试验结果
同样选定实测资料数据长度C为60,利用这60年的资料序列,分别运用马氏链点值预测方法和较优的时间序列预测方法预测后40年的数据值。马尔可夫链预测方法中选取的状态分级参数α=(α1,α2,α3,α4),如表4。
基于统计试验的预测结果如表5。表5中分别列出了试验次数N取50、200、800次的条件下的预测结果。
从服从三参数对数正态分布和P-III型分布的数据的预测误差分析表3和表5可以得出下面四个结论:(1)马尔可夫链点值预测方法的精度比时间序列分析预测方法要高;(2)马尔可夫链的三种点值预测方法中基于绝对分布的马尔可夫链点值预测方法的精度最低,其它两种点值预测方法预测精度相差不大;(3)马尔可夫链点值预测方法对不同的水文分布(三参数对数正态分布和P-III型分布)具有适应性;(4)序列的变差系数Cv和偏态系数Cs对两类预测方法的精度的影响显著。精度是随着Cv的增大而迅速下降,随着Cs的增大而有所提高。其他某些因素对预测精度的影响可参见文[9]。
4 结语
本文的结论仅限于服从P-III型分布或三参数对数正态分布的水文时间序列。文中所提出的基于马氏链状态预测的点值预测方法是一种比较简单的预测方法,本文的主旨在于基于统计试验的方法将其与时间序列分析预测方法进行比较,并未对点值预测做深入的研究。结论说明在水文时间序列预测中基于马氏链状态预测方法的点值预测方法更为有效,故可以更进一步地研究如何通过区间预测结果获得点预测值的方法,从而更有效地获得点预测值。
[1]张宸,林启太.模糊马尔可夫链状模型在矿区降水灾害预测中的应用[J].国外建材科技,2004,(1).
[2]郑文瑞,王新代,纪昆,王汉林.非确定数学方法在水污染状态风险评价中的应用[J].吉林大学学报,2003,(1).
[3]张文坚.90年代浙江城镇洪涝灾害分析及其展望[J].科技通报,1996,(1).
[4]宋印胜.马尔可夫链模型在地下水水位预测中的应用[J].山东地质,1998,(1).
[5]王渺林.灰色马尔可夫模型在寸滩站年最高水位预测中的应用[J].2004,(2).
[6]冯耀龙,韩文秀.加权马尔可夫链在河流丰枯状况预测中的应用[J].系统工程理论与实践,1999,(10).
[7]孙才志,林学钰.降水预测的模糊权马尔可夫模型及应用[J].系统工程学报,2003,(4).
[9]沈永梅.基于统计试验的马氏链点值预测方法和时间序列分析预测方法的比较分析[D].河海大学,2006.

