一种基于质量指导的InSAR相位解缠快速实现方法
李芳芳*①②④ 占 毅①②④ 胡东辉①② 丁赤飚①③
一种基于质量指导的InSAR相位解缠快速实现方法
李芳芳占 毅胡东辉丁赤飚
(中国科学院电子学研究所 北京 100190)(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)(微波成像技术国家重点实验室 北京 100190)(中国科学院研究生院 北京 100190)
相位解缠是干涉SAR数据处理中的关键步骤,解缠效果的好坏直接影响干涉测量的精度。该文针对质量指导的相位解缠方法需要进行大量排序操作,在干涉数据维度较大时解缠效率低下的问题,提出了一种基于堆排序的快速的质量指导相位解缠方法。首先通过干涉复数据对或干涉相位确定相位质量图。然后利用最大堆作为质量图排序的数据结构,通过对最大堆进行删除根结点、插入新结点操作的过程中始终保持最大堆的性质不变,从而实现了质量图的排序,完成了从高质量区域到低质量区域的相位解缠。与传统方法相比,基于堆排序的方法大大降低了计算的时间复杂度,对于干涉SAR大面积测绘应用具有十分重要的意义。最后,通过仿真和实测数据验证了算法的正确性和高效性。
干涉SAR;干涉相位;相位解缠;质量图;堆排序
1 引言
合成孔径雷达干涉测量技术(InSAR)是以SAR复数据提取的相位信息为信息源获取地表的3维信息和变化信息的一项技术。然而由于三角函数测量的限制,干涉相位被限制在之间,与真实的相位相差了的整数倍。因此必须进行相位解缠恢复模糊的相位周期从而获得目标的绝对干涉相位。相位解缠效果的好坏是影响InSAR测量精度的关键。
在过去的20多年里,InSAR相位解缠发展迅速,涌现出了大量的算法。但是由于InSAR干涉相位的复杂性,相位解缠仍是研究的难点和热点。目前的相位解缠算法,大致可以分为3类:路径跟踪法,最小范数法和基于网络规划的算法。路径跟踪法是一种局部算法,是基于逐像素的,通过不同的策略选择合适的积分路径,将误差限制在噪声区内,避免相位误差的传播。如枝切法通过识别残差点,设置正确的枝切线阻止积分路径穿过;质量指导法在相位质量图的引导下,从高相位质量数据开始积分,逐步向低相位质量的区域过渡,最大限度地避免误差的传递。与路径跟踪法不同,最小范数法是一种全局最优的算法,它将相位解缠问题转化为数学上求解最小范数的极值问题。使用最广泛的是最小二乘法,即在最小二乘意义下使展开相位梯度与缠绕相位梯度整体偏差最小。网络规划算法的主要思想是最小化解缠相位导数与缠绕相位导数之间的差异,并使其转化为比较成熟的网络优化问题,如何获取合适的权重矩阵是该算法的关键。
以上多种InSAR相位解缠算法,在实际的干涉处理中,路径跟踪法中的枝切法和质量指导法由于其算法简单易实现,且解缠结果比较准确,因而应用最为广泛。其中Goldstein提出的枝切法是经典的路径跟踪算法,该算法运算速度快,对内存需求小,它的不足之处在于没有利用其他的辅助信息,在残差点过于密集的情况下,枝切线难以正确设置,造成解缠误差。而质量指导法不是通过识别残差点的方法,而是使用辅助的相位质量信息控制相位解缠的路径,具有很高的解缠准确度。然而由于在相位解缠过程中需要对质量值进行排序以确定解缠的路径,因此大量的排序操作使得相位解缠的速度很慢。如何寻找一种快速有效的排序算法是提高相位解缠速度的关键。
针对上述关键问题,本文提出了一种基于堆排序的快速质量指导解缠方法,可以大幅缩短质量指导算法相位解缠的时间。本文的结构安排如下:第2节介绍了质量指导解缠算法的原理及质量图的确定;第3节介绍了利用最大堆进行质量图快速排序的方法;第4节通过仿真和实测数据处理结果验证了本文方法的有效性。
2 质量指导相位解缠
2.1 质量指导的路径跟踪策略
质量指导的路径跟踪法的关键步骤就是在相位质量图的指导下确定积分路径。其基本操作过程如下:
(1) 选择质量值最大的像素点作为种子点,同时将它标记为已解缠点,以它为基准对其4个相邻点分别进行相位解缠,解缠完成后标记为已解缠点,并将它们按质量值的高低存储到“邻接列”中。
(2) 从“邻接列”中移出质量值最高的像素点,以它为基准对4个相邻点中未被处理的点进行解缠并标记,并将它们按照质量值的高低加入到“邻接列”中。
(3) 重复步骤(2)直到“邻接列”为空,即所有像素点都已经解缠。
图1为质量指导的路径跟踪示意图。
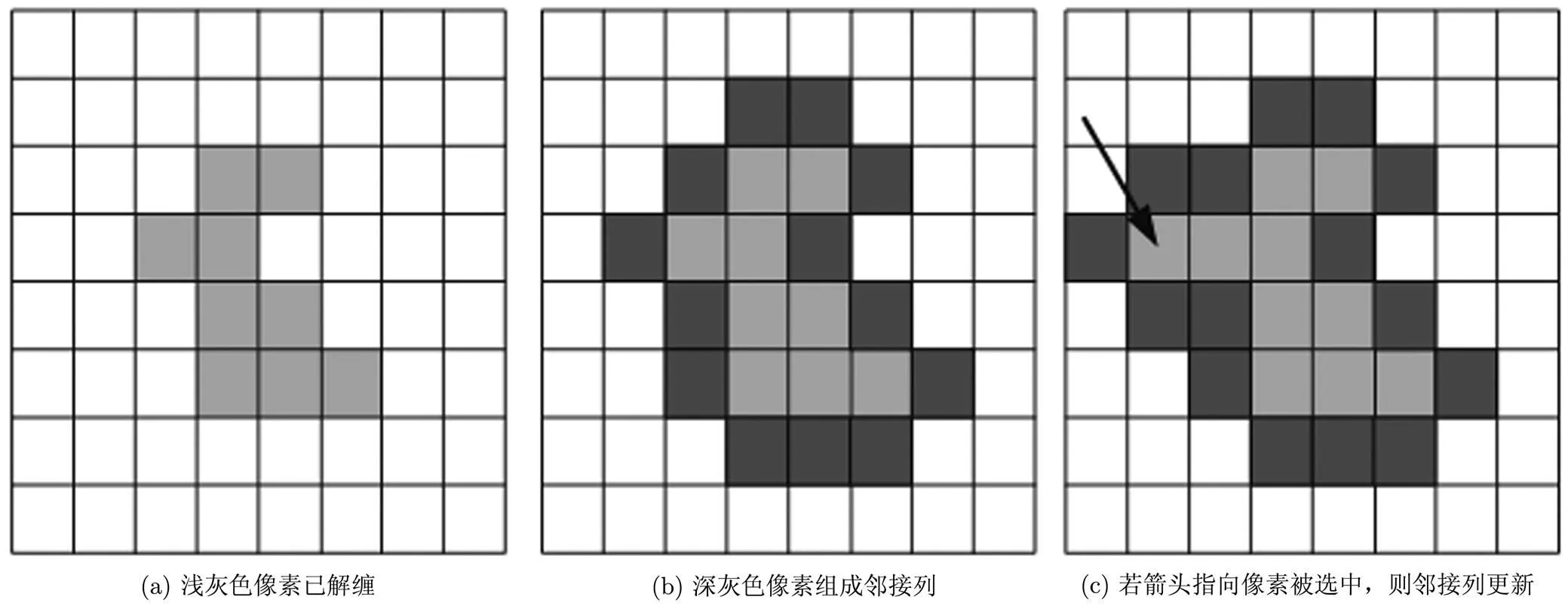
图1 质量指导的路径跟踪示意图
2.2 质量图的确定
对于InSAR相位,常见的相位质量图主要有4种:相干系数图、伪相干系数图、相位导数变化图、最大相位梯度图。其中,相干系数图的应用最广。相干系数值越高,表明图像对之间的相干性越好,即干涉相位的质量越好。对于InSAR复图像对和,其相干系数定义如下:

(2)
当无法获得SAR复图像对的强度值时,通常利用伪相干系数代替相干系数。伪相干系数计算如下:
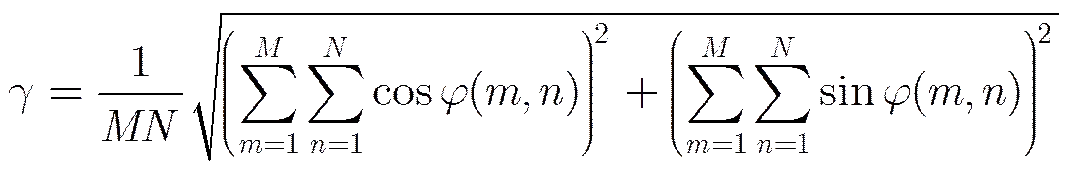
3 基于堆排序的快速算法
根据上节所述质量指导的路径跟踪策略可知,“邻接列”是一个有序的数组,按质量值的高低排序,每次取出质量最高的像素,解缠其相邻像素,并将它们按质量值高低插入“邻接列”,即路径跟踪的过程是不断从一个有序的数组中删除最大元素并插入新的元素,而且在插入后仍然保持其有序性不变的过程。常用的质量指导方法采用二分查找的方法插入新元素,其时间复杂度为,为“邻接列”的长度。在干涉相位数据维度较大时,插入查找过程会相当费时。文献[11]提出通过分块处理降低路径搜索的计算量,然而分块解缠后子数据块之间的相位合并是一难点,容易造成分块之间的相位不连续。为此,本文提出利用堆数据结构来实现在“邻接列”中快速插入新元素。
堆数据结构是一种数组对象,它可以被视为一棵完全二叉树。树中每个结点与数组中存放该结点值的那个元素对应。树的每一层都是填满的,最后一层可能除外。设数组为堆,它还满足如下的性质:

对最大堆进行操作的一个重要的子程序为保持堆的性质,其输入为数组和位置,假设以的左孩子和右孩子为根的两棵二叉树均为最大堆,但可能小于其子女,违反了最大堆性质。调整的过程是使在堆中不断下降直到满足最大堆的性质。在最坏的情况下,该操作作用于一个高度为的结点的时间复杂度为。在建立最大堆、删除根结点的过程中均要用到保持堆性质这一子程序。
根据2.1节中的质量指导路径跟踪的操作步骤可知,对于以最大堆为数据结构的“邻接列”来说,需要进行以下几种操作:
(1) 初建最大堆。对应2.1节中的步骤(1),即将种子点相邻像素的质量值作为关键字,建成最大堆。由于仅考虑上下左右4个方向的相邻像素,因此,初始堆最多只有4个元素。建堆的过程就是对数组中所有非叶子结点,按位置从大到小均执行一次保持堆性质的操作,就可形成最大堆。图2显示了初始建堆的过程。
(2) 删除最大堆的根结点,并将剩余元素调整为最大堆。对应2.1节的步骤(2)中取出“邻接列”中质量值最高的像素点。根结点为数组中第1个元素,通过交换第1个元素与最后一个元素,并将数组的长度减1实现删除,对新的根结点执行保持堆性质的操作,从而将剩余元素重新调整为最大堆。图3为删除根结点的过程。
(3) 插入新结点,并将新数组调整为最大堆。对应2.1节的步骤(2)中将当前处理像素的相邻像素按照质量值的高低加入到“邻接列”中。首先在数组的最后增加一个元素,以当前处理像素的一个相邻像素的质量值作为关键字,然后将该新增结点不断与其父结点相比,若该元素的关键字较大,则交换它们的关键字,继续向上移动直至元素的关键字小于其父结点,此时将新数组调整为最大堆。图4为插入一个新结点的过程。
下面具体分析上述3个步骤的时间复杂度,由于建立初始最大堆时最多只有4个元素,与其它过程相比,其运行时间可忽略。对于包含个元素的堆,其高度为,因此删除根结点并调整为最大堆的时间复杂度为。插入新结点时,新结点到根结点的路径长度即为高度,故插入新结点并调整为最大堆的时间复杂度也为。
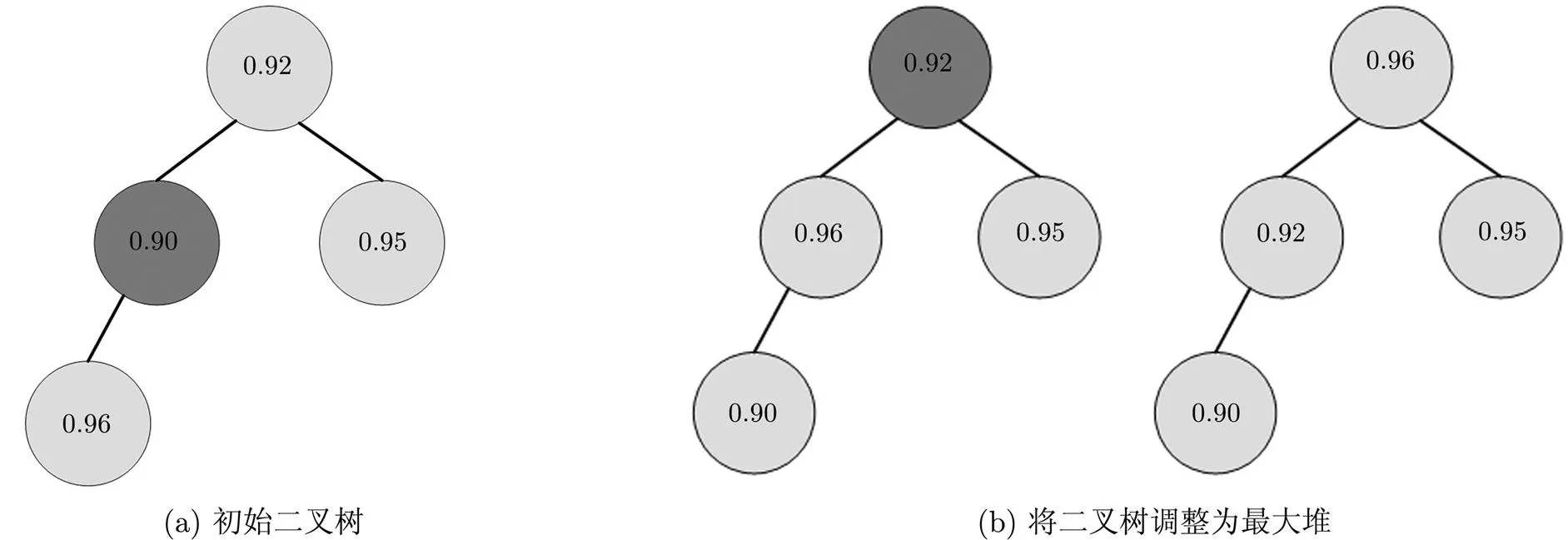
图2 建立初始最大堆示意图(其中深灰色结点表示待执行保持堆性质操作的结点)
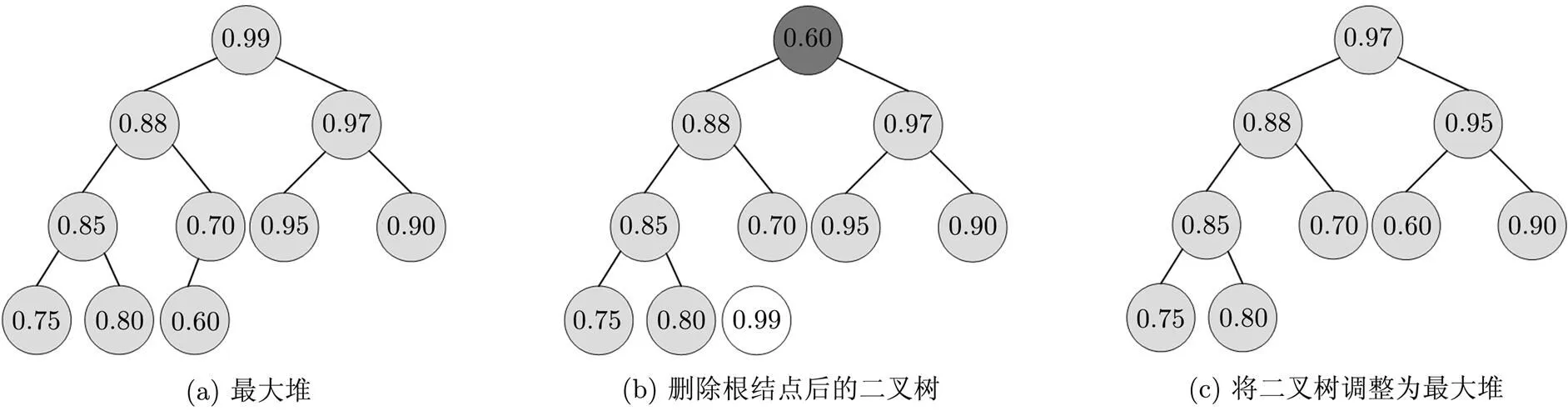
图3 最大堆删除根结点示意图(其中深灰色结点表示待执行保持堆性质操作的结点)
图4 最大堆插入新结点示意图(其中深灰色结点表示与新增结点相比较的父结点)
4 实验结果与分析
本节分别通过仿真实验和实测数据,分析比较了枝切法与质量指导法的精度,对比了本文方法与传统质量图解缠方法的计算效率,验证了本文方法的有效性。
4.1 仿真实验
根据Isolation Peak, Colorado区域的DEM仿真的干涉条纹如图5(a)所示,其真实相位如图5(b), 图5(c)为相干系数图,其中的低相干区域大多由于SAR图像中的叠掩现象引起。图5(d)-5(g)对比了利用枝切法和以相干系数图为质量图的质量指导法解缠的结果及误差图,其中图5(e)和图5(g)中的白色区域为存在解缠误差的区域,可以看出,枝切法解缠的误差区域更多,尤其是在图像的下方,出现了较大面积的解缠误差,这是由于在残差点密集区域容易造成枝切线设置不当,使得积分路径从低质量的区域穿过,导致了相位误差的传播。而质量指导方法则避免了积分路径不当引起的误差,图5(g)中的误差区域基本上限制在低相干区域。由此可见,质量指导法在获得可靠质量图的情况下比枝切法的解缠效果更好。
4.2 实测数据实验
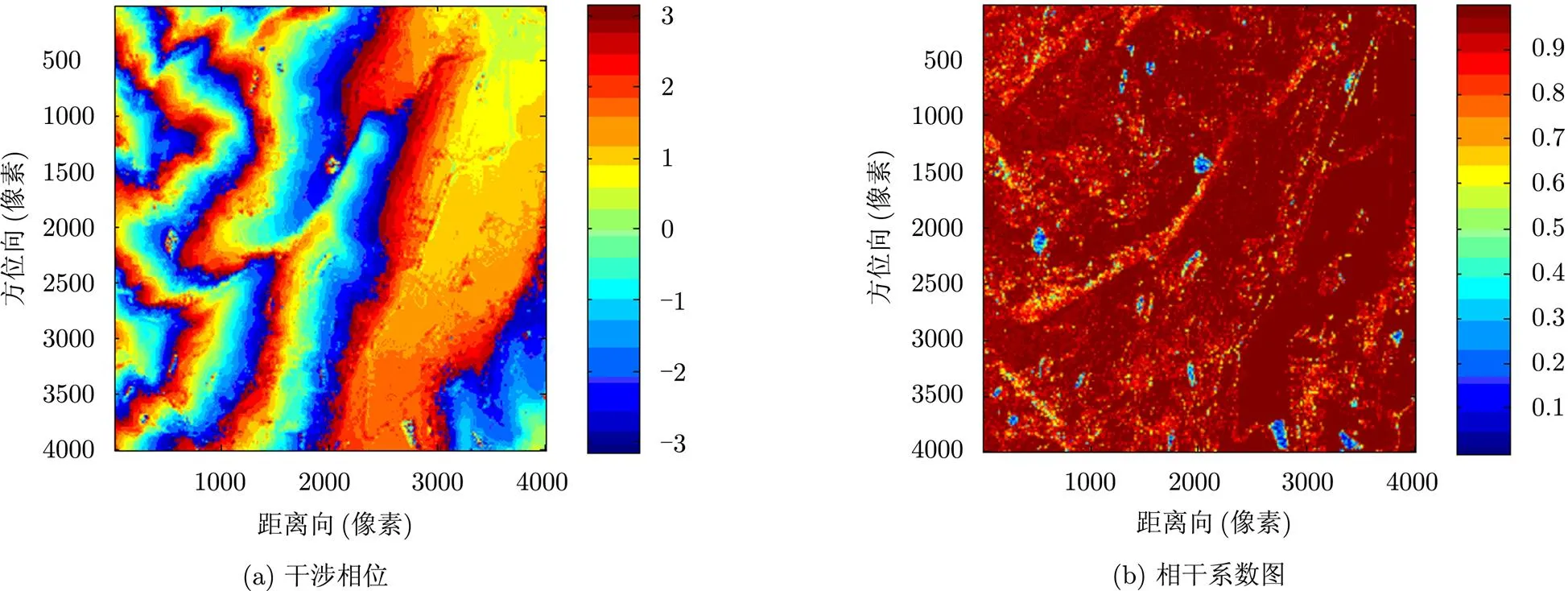
本节采用两块实测数据验证本文方法,实验所用数据为中国科学院电子学研究所的X波段机载双天线InSAR系统飞行实验数据,图6为2010年长治地区的实验数据,图7为2011年绵阳地区的实验数据。图6(a)和图7(a)均为经过去平地效应和相位滤波后的干涉相位,图6(b) 和图7(b)分别为各自的相干系数图,以此作为质量图进行质量指导相位解缠结果如图6(c)及图7(c),可以看出解缠后的相位不一致区域都限制在低相干区域。图6(d)和图7(d)为各自的解缠相位重新缠绕后的干涉相位图,与图6(a)及图7(a)相比基本一致,计算出二者之间的均方误差分别为0.005 rad, 0.006 rad,该误差很小,可以忽略,由此表明了解缠过程没有引起相位误差的传播,验证了质量指导算法的有效性。
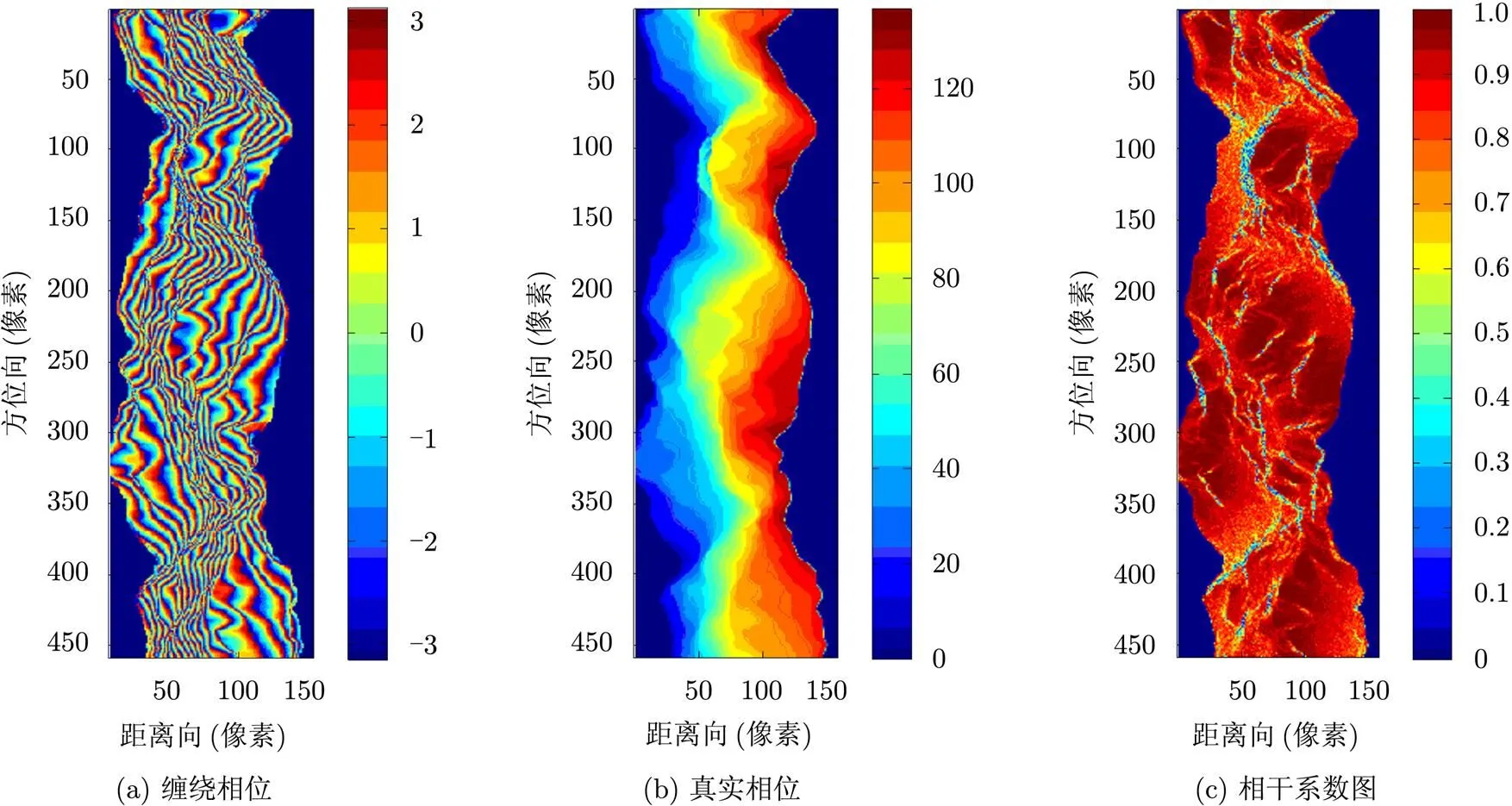
表1对比了用本文基于堆排序的质量指导路径跟踪方法和传统质量指导法解缠不同大小的实测干涉相位图的运行时间。两种方法在同一台计算机上运行(Core i5 3.10 G CPU, 2 G内存),利用Visio Studio 2010实现。通过对比可以看出,本文提出的方法在计算效率上明显优于传统方法,而且随着干涉相位数据的增大,加速比增大,这与上一节中对本文方法与传统方法时间复杂度的对比分析相一致。因此,本文方法可用于解决干涉SAR在大面积测绘时大块干涉相位图解缠的效率问题。
表1 本文算法与传统质量指导算法所用时间对比

图像尺寸本文方法运行时间(s)传统方法运行时间(s)加速比 1024×10243.1257.2502.32 2048×204812.12551.0154.21 4096×409651.125398.5157.80 8192×8192247.5533137.72012.68
5 结束语
本文提出了一种快速的基于质量图指导的InSAR相位解缠方法。质量指导法利用辅助的相位质量信息控制相位解缠的路径,具有很高的解缠准确度。然而在路径跟踪过程中需要对质量图进行大量排序操作,使得质量指导法的效率低下,针对这一问题本文提出了一种基于堆排序的快速质量指导相位解缠方法。该方法的时间复杂度正比于堆的高度,即,与传统二分查找方法的时间复杂度相比,本文方法大大提高了计算的速度,而且随着干涉相位数据维数的增大,加速比增大,解决了大块干涉相位图解缠效率低下的问题,对于干涉SAR大面积测绘应用具有十分重要的意义。另外,在实际干涉相位图中,由于地形的复杂变化,相干系数图并不能准确反映相位质量的好坏,从而导致解缠误差,因此,如何得到准确可靠的相位质量图是需要进一步研究的内容。

[1] Rosen Paul A, Hensley Scott, Joughin Ian R,.. Synthetic aperture radar interferometry[J]., 2000, 88(3): 333-382.
[2] 王超, 张红, 刘智. 星载合成孔径雷达干涉测量[M]. 北京: 科学出版社, 2002: 100-103.
Wang Chao, Zhang Hong, and Liu Zhi. Spaceborne Synthetic Aperture Radar Interferometry[M]. Beijing: Science Press, 2002: 100-103.
[3] Goldstein Richard M, Zebker Howard A, and Werner Charles L. Satellite radar interferometry: two-dimensional phase unwrapping [J]., 1988, 23(4): 713-720.
[4] Flynn Thomas J. Consistent 2-D phase unwrapping guided by a quality map[C]. Geoscience and Remote Sensing Symposium Proceedings, IGARSS’96, 1996: 2057-2059.
[5] 魏志强, 金亚秋. 密集残差点区域的解缠算法[J]. 遥感学报, 2009, 13(1): 54-59.
Wei Zhi-qiang and Jin Ya-qiu. Registration and phase unwrapping algorithms for InSAR images with dense residues[J].,2009, 13(1): 54-59.
[6] Zhao M, Huang L, Zhang Q,.. Quality-guided phase un- wrapping technique: comparison of quality maps and guiding strategies [J].,2011, 50(33): 6214-6224.
[7] Pritt Mark D and Shipman Jerome S. Least-squares two- dimensional phase unwrapping using FFT [J]., 1994, 32(3): 706-708.
[8] Zhang K, Ge L, Hu Z,. Phase unwrapping for very large interferometric data sets [J]., 2011, 49(10): 4048-4061.
[9] Chen Curtis W and Zebker Howard A. Phase uwrapping for large SAR interferogram: statistical segmentation and generalized network models[J]., 2002, 40(8): 1709-1719.
[10] Ghiglia Dennis C and Pritt Mark D. Two-dimensional Phase Unwrapping: Theory, Algorithms, and Software [M]. New York: John Wiley & Sons, 1998: 122-236.
[11] 黄柏圣, 许家栋. 一种基于新质量图引导的干涉相位快速解缠方法[J]. 系统仿真学报, 2010, 22(2): 528-531.
Huang Bai-sheng and Xu Jia-dong. Fast phase unwrapping method for interferometric phase based on new quality- guided[J]., 2010, 22(2): 528- 531.
[12] Cormen Thomas H, Leiserson Charles E, Rivest Ronald L,.. Introduction to Algorithms (Second Edition) [M]. London: The MIT Press, 2001: 73-82.
A Fast Method for InSAR Phase Unwrapping Based on Quality Guide
Li Fang-fangZhan YiHu Dong-huiDing Chi-biao
(Institute of Electronics Chinese Academy of Sciences, Beijing 100190, China)(Key Laboratory of Spatial Information Processing and Application System Technology, Chinese Academy of Sciences, Beijing 100190, China)(The National Key Laboratory of Microwave Imaging Technology, Beijing 100190, China)(Graduate University of Chinese Academy of Sciences, Beijing 100190, China)
Phase unwrapping is a key issue in InSAR research. As a critical step of InSAR processing, it affects the accuracy of interferometry measurement directly. The efficiency of the traditional quality-guided phase unwrapping method is low due to a great deal of sorting, espceically for large interferogram. This paper proposes a highly efficient quality-guided phase unwrapping method based on heap sort in order to solve the problem. First, the quality map is caculated according to the interferometric complex data or interferogram. Next, with the max-heap acting as the data structure of sorting, its property is maintained while deleting root node and inserting new node, and thus the sorting of quality map is accomplished and the phase can be unwrapped from high quality areas to low quality areas. The improved algorithm reduces the computational complexity greatly compared with traditional methods, which is significant in large area mapping of InSAR. At the end of the paper, the simulated and experimental results show the accuracy and the efficiency of the algorithm.
Interferometric SAR (InSAR); Interferometric phase; Phase unwrapping; Quality map; Heap sort
TP391
A
2095-283X(2012)02-0196-07
10.3724/SP.J.1300.2012.20023
2012-04-11收到,2012-06-15改回;2012-06-20网络优先出版
国家863计划(2007AA120302)资助课题
李芳芳 liff86@gmail.com
李芳芳(1986-),女,博士生,研究方向为干涉SAR信号处理。
E-mail: liff86@gmail.com
占毅(1986-),男,硕士生,研究方向为SAR信号干扰抑制。
E-mail: zhanyixiaolu@gmail.com
胡东辉(1970-),男,副研究员,研究方向为SAR/ISAR成像。
E-mail: dhhu@mail.ie.ac.cn
丁赤飚(1969-),男,研究员,博士生导师,现任中国科学院电子学研究所副所长。主要从事合成孔径雷达、遥感信息处理和应用系统等领域的研究工作。
E-mail: cbding@mail.ie.ac.cn

