基于Radon变换和Jeffrey散度的SAR图像变化检测方法
郑 瑾*①②③ 尤红建①②
基于Radon变换和Jeffrey散度的SAR图像变化检测方法
郑 瑾尤红建
(中国科学院电子学研究所 北京 100190)(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)(中国科学院研究生院 北京 100049)
针对多时相合成孔径雷达(Synthetic Aperture Radar, SAR)图像的变化检测,该文采用Radon变换将局部图像投射成投影,用Edgeworth展开来逼近投影的统计分布,比较投影之间的概率分布变化,并引入Jeffrey散度作为两种分布差异的衡量因子,从而计算两个时相SAR图像之间的变化差异图像。投影片断保留了一定量的图像结构信息,弥补了局部概率密度不变时的检测漏洞,而Jeffrey散度具有较好的数值稳定性和对噪声的鲁棒性。最后通过实际的星载SAR图像实验,验证了该文算法的有效性。
SAR (Synthetic Aperture Radar)图像;变化检测;Edgeworth展开;Radon 变换;Jeffrey散度
1 引言
Synthetic Aperture Radar (SAR)传感器具有全天候全天时获得数据的特性,能适应各种天气且不受白天黑夜的影响。因此SAR图像成为遥感应用领域的一个重要工具,其中一个重要的应用就是利用已配准的多时相SAR图像进行变化检测。近年来,SAR变化检测的应用扩展已经到了环境观测、灾害评估、国家安全和其它领域。
国内外研究人员对变化检测的算法进行了深入而广泛的研究,例如图像差值法、比值法、似然比法、主成分分析法等。然而,针对SAR图像的变化检测方法仍显不足,究其原因,是因为SAR有着比较独特的成像机理。SAR图像是地面多个散射单元合成的结果,使得SAR带有斑点噪声,而且获取数据的雷达参数也会影响SAR变化检测的最终效果,因此对于SAR图像的变化检测,多数采用基于局部统计特性比较的方法。最经典的方法是均值比法,能降低斑点噪声对变化检测的影响,但它只局限于一阶统计量的比较。事实上,高阶统计量包含了更多概率密度函数的信息,例如,3阶中心矩体现对称性而4阶中心矩可以衡量分布的形状的高瘦或矮宽。Inglada等人将Pearson模型引入了Kullback-Leibler(KL)散度,但Pearson模型只能描述8种分布类型。后来,他又提出了基于累量的交叉熵,采用Edgeworth展开来估计SAR图像的分布密度,但其前提是要求待估计的分布离高斯分布不远。
针对这些方法均需要事先假设分布模型的不足,本文提出了一种不依赖于模型假设的统计分布比较的方法。基本的思想是将待估计的随机样本变换成一个服从已知分布的随机变量。为此,我们采用Radon变换将原样本变换成服从近似高斯分布的投影变量。然后,采用Edgeworth展开方法自适应逼近投影变量的概率分布,并引入Jeffrey散度作为两个分布之间差异程度的变化因子,对星载SAR 图像进行变化检测试验。
本文的结构安排如下:第2节介绍了基于Edgeworth逼近的交叉熵变化检测方法,第3、第4节分别对该方法的分布估计和散度计算两个环节的不足提出了修改,第5节介绍了本文实验中用到的CFAR阈值分割方法,第6节为结束语。
2 基于Edgeworth逼近的交叉熵
SAR变化检测的最关键的问题是要根据两幅不同时间获取的SAR图像计算出它们之间的变化情况。SAR图像所具有的统计特性使单一的像素点并不具有实际意义,解译和处理图像都建立在一定数量像元的集合上,因此我们在应用各种变化检测算法时都会取一个样本窗口,以窗口包含的像素为整体运行算法,样本窗口遍历整个图像后得到最终的变化检测结果,具体算法流程如图1所示。
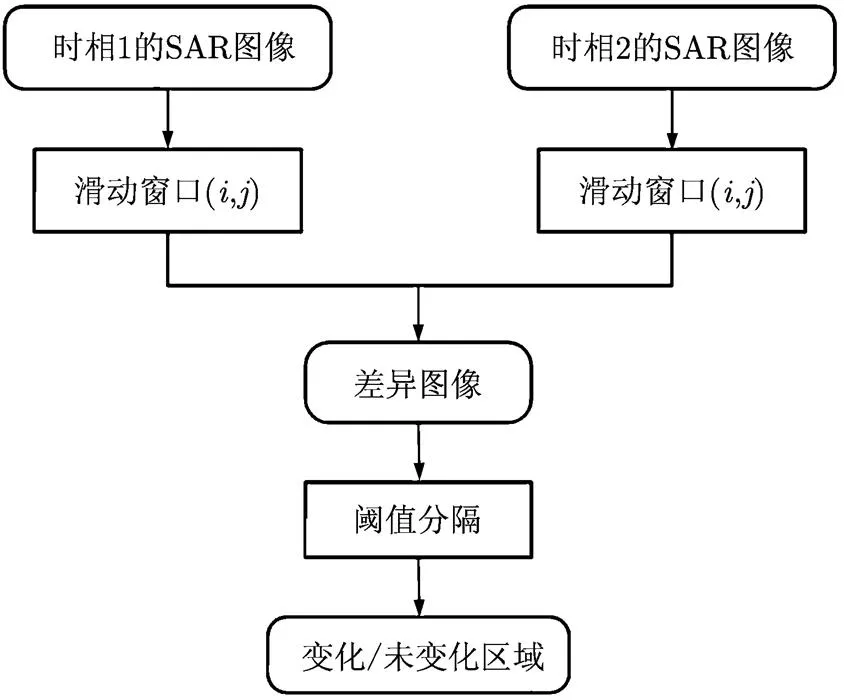
图1 SAR图像变化检测算法流程图

由式(1)可知,计算交叉熵数值必须首先获得图像的概率密度函数。我们知道,成像得到的SAR数据,其图像中的任何一个图像是地面目标的多个散射单元的合成效果,它是多个随机变量的叠加。研究发现,SAR回波数据在一个区域内的分布是比较均匀的,其统计上有一定的分布规律,一般可以采用一种分布模型进行描述,为此人们给出了很多个适合SAR图像的分布模型,比如K分布、Gamma分布等。而实际上,不同的地面场景,所得到的统计分布规律也有较大的差别。此外SAR图像的分布规律还会随着SAR的波段、图像的分辨率的不同而变化。为了准确描述各种场景、不同波段和不同分辨率的SAR图像的分布模型,我们采用Edgeworth级数展开逼近的方法自适应地描述SAR图像的分布模型。Edgeworth级数展开逼近的本质是利用与待估计分布相同均值和方差的高斯分布及多项式进行逼近。假设是与有相同均值和方差的高斯分布,截断到6阶的表达式为
(2)
将式(2)代入式(1),即得到基于统计累量的交叉熵(Cumulant-based KL Divergence, CKLD),文献[8]给出了详细推导过程,文献[7]中也给出了CKLD截断到4阶的表达式
(3)
其中,

为了解决不对称性,通常采用
(4)
然而,Edgeworth级数展开逼近的方法依赖于待估计分布离高斯分布模型不远的假设条件,因此,当假设不满足时,Edgeworth逼近便会失效。图2显示了一个非高斯分布的场景用Edgeworth逼近其分布的例子。图2(a)显示了拍摄于Ottawa区域的SAR图像中切取的一个150×150像素大小的感兴趣区域。图像为城市区域,有较多的人造地物和强散射目标,因此直方图呈现明显的长拖尾形状,特殊场景的分布(如城市区域)或严重的斑点噪声都能造成长拖尾的形成,在这种情况下Edgeworth估计就发生了错误(图2(b))。为了解决这一局限性,本文引入了Radon变换的思想,利用滑窗和Radon变换的累加性生成近似局部高斯变量,满足了CKLD的前提条件。
3 基于Radon变换的图像投影片断
如上文所述,局部分布中的长拖尾通常由严重的斑点噪声或特殊场景分布(如规则形状的建筑物、直线型的机场跑道等)造成。Radon变换具有增强线形目标的特性,对于具有机场跑道、港口码头等直线性目标的场景具有较好的应用效果。对于一个给定的像素,将其邻域的像素点沿着一个与坐标轴成角的方向求灰度平均值,得到一个“投影变量”,记为。投影过程用Radon变换的定义式来表达为下式

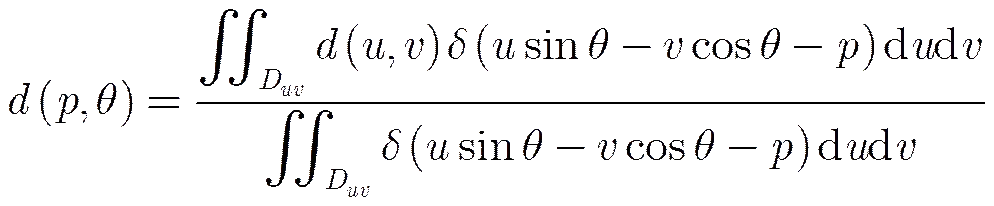
图3 Radon 变换的示意图

基于投影的变化检测的另一有益之处在于它能检测到一些不改变均值或图像概率分布的变化,如纹理的旋转等,这是因为投影包含了一定的空间结构信息。Radon变换可以理解为图像在-空间的投影,-空间的每一点对应图像空间一条直线。因此在-空间做像素级的变化检测,相当于在原始图像空间做直线型结构级别的变化检测。在某一方向将像素“堆积”,便得到这个方向的投影片断,利用足够多的不同方向的投影片断就可以重建原始图像。计算机断层扫描(CAT扫描)就是该理论在医学上的成功应用。因此基于投影的方法可以检测到更细微的变化。鉴于投影片断所包含的诸多优点,本文提出一种新的SAR图像变化检测方法,基于投影的CKLD方法(Projection-based CKLD, PCKLD),定义如下:

(3) 按式(7)计算分析窗内像元集合的PCKLD距离;
(4) 移动分析窗,重复(1) - (3),遍历整个图像,获得变化差异图。
为了更好地理解基于投影的变化检测算法的优势,我们做了一些仿真实验。仿真数据(图4(a)和图4(b))面积为100×100像素,变化区域为40×40像素,亮条纹灰度值为255,暗条纹灰度值为64,图4(b)中的变化是由图4(a)的相同区域经过旋转得到的。为了仿真SAR图像的斑点噪声,每个像素点都加上了20个从中均匀分布产生的随机相位,然后计算每个像素的模的平方,分别得到图4(c)和图4(d)。
为了评价变化检测结果的优劣,我们引入接受者操作特性(Receiving Operator Characteristics, ROC)曲线,它反映的是检测率对虚警率的敏感度。在同一虚警率水平下,曲线越高表示检测率越高,性能越好。我们用5×5和7×7的滑动窗口分别遍历图像,得到了图5所示的两组对比ROC曲线,体现了采用投影方法以后的检测纹理变化时的优势。CKLD的ROC曲线基本呈一条对角线,表明接近于随机猜测,即没有检测到纹理的变化,而PCKLD则效果好很多,尤其是当滑动窗尺寸变大时,PCKLD的检测正确率明显提高。

图4 仿真数据及加上随机相位后的仿真SAR数据

图5 CKLD与PCKLD分别在两种尺度下对纹理变化的检测结果ROC曲线对比
4 基于Jeffrey散度的差异值计算
在实际应用CKLD的过程中会遇到一些问题,例如图像局部若发生突变或者斑点噪声严重,会导致该区域的灰度值方差变大,而方差在CKLD方法中占有比较重要的地位,方差的不稳定会导致计算的距离值也不稳定。Jeffrey散度是KL散度的修正版本,具有数值稳定性和对噪声的鲁棒性,受方差不稳定影响较小,它的定义是


(10)
这样就得到了基于累量的Jeffrey散度的计算方法(Cumulant-based Jeffrey divergence),因Jeffrey散度本身就具有对称性,故可直接作为距离值使用,因此样本、之间的Jeffrey距离值为
为了分析比较KL散度和Jeffrey散度的数值稳定性,我们考虑一个简化的例子:。Jen-Jen Lin等人在文中提到,式(3)的第2项是主要项,其它都可推入误差项:
(12)
把式(12)分别代入式(4)和式(9),得到经过简化的CKLD和CJD的距离表达式
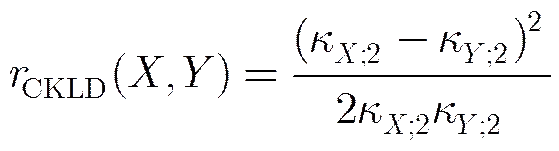
(14)
由上两式可看出,方差的不稳定性在式(13)中被放大了,而在式(14)中却被削弱了。图6显示了CJD在减弱SAR图像方差不稳定性上的优势,横轴为方差与的对数比,纵轴为由式(13)和式(14)定义的与之间的距离值。
5 基于CFAR检测的阈值分析
恒虚警率(Constant False Alarm Rate, CFAR)检测是雷达自动目标检测的一个重要组成部分,它的实质是针对不同背景来调整虚警概率到指定的等级。CFAR检测的关键技术是确定杂波分布模型和指定虚警率,然后计算出分割阈值。假设为雷达杂波分布模型的概率密度函数,其概率分布函数为
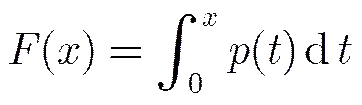
(16)

图6 距离与方差之间的关系曲线

图7 CFAR阈值分割示意图

6 星载SAR图像变化检测的试验
以上我们分析了投影变换和Jeffrey散度带来的优势,结合这两个改进,将该新方法叫做基于投影的CJD(Projection-based CJD, PCJD),我们用真实星载SAR图像进行了实验。图8(a)和图8(b)为已配准的两个时相的Radarsat-2 SAR图像,分别在2008年和2009年获取的,图像大小为500×500像素,地面分辨率为3 m。通过研究和试验,该数据的取样窗口在11×11时比较合适。为了检验变化检测的效果,我们采用人工的方法勾画出变化的白色区域,得到图8(c)。图9是用CKLD, PCKLD和PCJD 3种变化检测方法计算得的差异图和用CFAR检测方法自动提取的变化区域。进行CFAR阈值分割时,为简便起见,假设杂波分布模型为高斯分布,并设置恒虚警率为0.01,计算阈值后对变化差异图进行二值化。比较CKLD与PCKLD的变化区域,我们发现基于投影的方法检测到更多的变化区域,但是也增加了许多的虚警点,这是因为检测到了更多细微的变化;比较PCKLD与PCJD,可以发现PCJD减少了不少虚警点但保留了正确检测的变化点,究其原因,是因为Jeffrey散度的数值稳定性减少了许多因方差变化而增加的虚警点。图10显示了3种方法的ROC曲线,可以看出,PCJD的ROC曲线优于另外两种方法,在同一虚警率水平下保持了较高的检测率。图11显示了ROC曲线上各点到最优点()的距离与阈值的关系曲线,当曲线取到极小值时就表明相应的阈值为最优阈值。当3条曲线取到各自的最优阈值时,PCJD方法的极小值最小,并且曲线不尖锐,敏感度较低,检测结果在阈值有微小变化时差异并不大,最佳阈值大约在[40, 50]之间。

图8 数据和地面变化参考图

图9 变化检测结果图
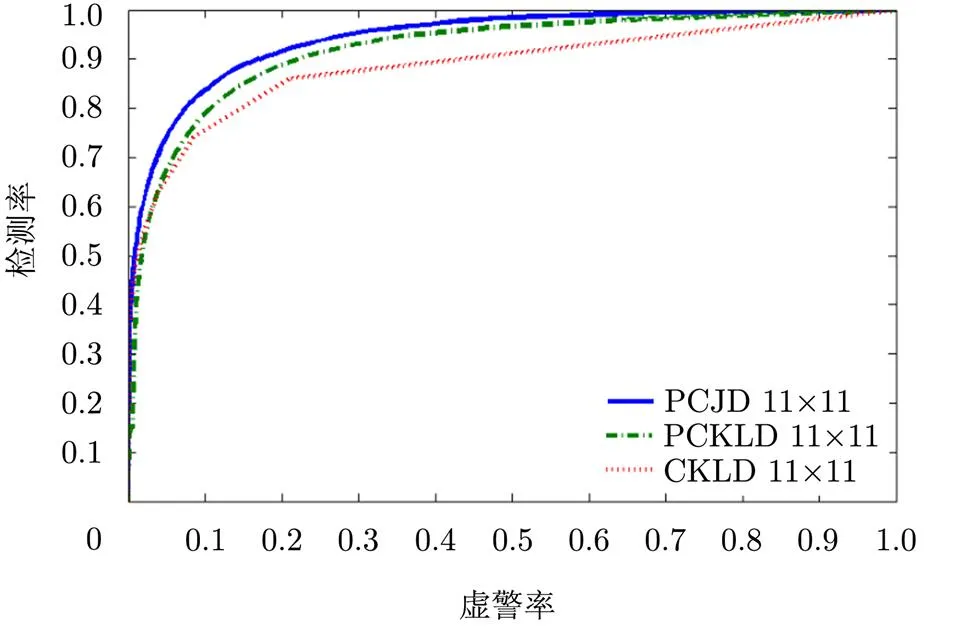
图10 检测结果的ROC曲线图
7 结束语
本文针对基于统计分布的变化检测存在的不足,提出了一种基于Radon变换和Jeffrey散度的变化检测方法。通过采用Radon变换将局部图像投射成两个投影,投影的直方图比较接近于高斯分布,使Edgeworth展开能更好地逼近其分布。在比较投影之间的分布变化时考虑了图像的空间结构信息,因此有更好的检测效果。Jeffrey散度的应用改善了KL散度在实际检测中的数值不稳定性,特别是SAR的斑点噪声导致的方差不稳定对KL散度影响很大。通过实际的SAR图像进行了实验,表明本文提出的变化检测方法具有较高的检测率。
[1] Karjalainen M, Hyyppa J, and Devillairs Y. Urban change detection in the Helsinki metropolitan region using Radarsat-1 fine beam SAR images[C]. Remote Sensing and Data Fusion over Urban Areas, 2003, 2nd Geoscience and Remote Sensing Society/International Society for Photogrammetry and Remote Sensing Joint Workshop on, Berlin, Germany, May 2003: 273-277.
[2] Ridd Merrill K and Liu Jiajun. A comparison of four algorithms for change detection in an urban environment[J]., 1998, 63(2): 95-100.
[3] Hame T, Heiler I, and Miguel-Ayanz J S. An unsupervised change detection and recognition system for forestry[J]., 1998, 19(6): 1079-1099.
[4] Goodenough D G, Chen Hao, and Dyk A. Evaluation of Convair-580 and simulated Radarsat-2 polarimetric SAR for forest change detection[C]. International Geoscience and Remote Sensing Symposium, IEEE International Conference, Denver, USA, 2006: 1788-1791.
[5] Ashbindu Singh. Review Article Digital change detection techniques using remotely-sensed data[J]., 1989, 10(6): 989-1003.
[6] Inglada J. Change detection on SAR images by using a parametric estimation of the Kullback-Leibler divergence[C]. International Geoscience and Remote Sensing Symposium, IEEE International Conference, Toulouse, France, 2003(6): 4104-4106.
[7] Inglada J and Mercier G. A new statistical similarity measure for change detection in multitemporal SAR images and its extension to multiscale change analysis[J].2007, 45(5): 1432-1445.
[8] Lin Jen-jen, Saito Naoki, and Levine Richard A. Edgeworth approximation of the Kullback-Leibler distance towards problems in image analysis[OL]. http://www.math.ucdavis. edu/~satio. 1999.
[9] Murphy Lesley M. Linear feature detection and enhancement in noisy images via the Radon transform[J]., 1986, 4(4): 279-284.
[10] Kerekes J. Receiver operating characteristic curve confidence intervals and regions[J].2008, 5(2): 251-255.
[11] Puzicha J, Hofmann T, and Buhmann J M. Non-parametric similarity measures for unsupervised texture segmentation and image retrieval[C]. IEEE Computer Society Conference, Computer Vision and Pattern Recognition, Washington, D.C., USA, 1997: 267-272.
Change Detection with SAR Images Based on Radon Transform and Jeffrey Divergence
Zheng JinYou Hong-jian
(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)(Key Laboratory of Technology in Geo-spatial Information Processing and Application System, Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)(Graduate University, Chinese Academy of Sciences, Beijing 100049, China)
Focusing on the change detection with multitemporal Synthetic Aperture Radar (SAR) images, this paper presents a new approach based on the comparison of the density of the projections produced by Radon transform. The projections include the structure information, which helps when the local statistical distribution does not change. Edgeworth approach is used to fit the statistical distribution model of the projections. Jeffrey divergence is proposed as a measurement of the difference between two densities for that it is numerically stable and robust with respect to noise. This approach is demonstrated feasible according to the processing test using real satellite SAR images.
Synthetic Aperture Radar (SAR) images; Change detection; Edgeworth approach; Radon transform; Jeffrey divergence
TN957.52
A
2095-283X(2012)02-0182-08
10.3724/SP.J.1300.2012.10068
2011-12-31收到,2012-04-09改回,2012-04-12网络优先出版
郑瑾 zhengjin09@mails.gucas.ac.cn
郑瑾(1987-),女,浙江绍兴人,2009年获北京航空航天大学学士学位,并进入中国科学院电子学研究所攻读硕士学位。研究方向为SAR图像处理及应用。
E-mail: zhengjin09@mails.gucas.ac.cn
尤红建(1969-),男,1992年获武汉测绘科技大学(现属武汉大学)学士学位,1995年获清华大学硕士学位,2001年获中国科学院遥感应用研究所博士学位。现工作于中国科学院电子学研究所,担任研究员,博士生导师。承担过863、国家自然科学基金等国家级项目,已经出版专著两部,以第一作者发表学术论文近五十篇。目前主要从事遥感图像处理和应用领域的研究。
E-mail: hjyou@mail.ie.ac.cn

