基于风险价值模型的干散货二手船交易风险测度
陈莉,王学锋,郑士源
(上海海事大学交通运输学院,上海 201306)
二手船交易市场是船舶所有人进入或退出航运市场、快速增减运力的重要途径,近年来日渐繁荣.据上海航运交易所统计,2010年全球二手船市场交易总额达275.52亿美元,但是受航运市场价格波动的影响,二手船交易价格显现出更加强烈的波动性,在一年内甚至出现20%以上的跌幅;由于船舶价格高昂,掌握二手船交易可能出现的损失及其概率并把握好二手船交易时机显得极为紧迫且重要.二手船是指经过一段时间的营运使用后,由原船舶所有人将其转手出售给新船舶所有人,继续投入营运使用的旧船.二手船交易的主要动机在于船队更新、投机和船队扩张,参与者可以利用市场的波动性获利.[1]由于船舶买卖多数都通过融资进行,二手船价格不仅受到船舶所有人的重视,也受到投资者、银行和造船厂的关注.
国内外对二手船价格的波动率研究较为成熟,在干散货船、油船等细分市场均有所涉及,如KAVUSSANOS[2],MANOLIS 等[3]分别使用自回归条件异方差(AutoRegressive Conditional Heteroskedasticity,ARCH)和广义自回归条件异方差(Generalized AutoRegressive Conditional Heteroskedasticity,GARCH)模型对二手船价格的波动性进行建模;蔡立明等[4]则对巴拿马型散货二手船价格建立适当的ARIMA模型;本文在上述文献的基础上采用基于广义误差分布的自回归条件异方差(Generalized AutoRegressive Conditional Heteroskedasticity based on General Error Distribution,GARCH-GED)模型能更好地考虑价格序列的厚尾性.
国内外在金融市场的风险测度中广泛应用风险价值(Value at Risk,VaR)模型,近几年在干散货运价及其衍生品FFA上的应用也不少.王辉[5]、马国强[6]使用VaR模型对干散货市场的运价进行风险定量分析,于圆[7]、刘萍等[8]、SYRIOPOULOS 等[11]使用VaR模型对干散货运价的衍生品FFA及航运企业股票投资组合进行风险测度;KAVUSSANOS等[12]首次采用风险测量 VaR模型结合 ETL(Expected Tail Loss,又称损失期望值(Expected Shortfall,ES))对油船运费市场进行风险测度.但是用VaR模型对二手船船价交易风险进行研究的却甚少,对二手船交易的风险测度研究主要集中在定性的分析和介绍上,如 AMIR 等[13]和李云光[14]介绍航运企业的风险定义、风险特征、风险主要成因和风险不同测度方法等,但上述文献均限于对风险的定性分析,没有进行定量分析.
结合上述国内外研究现状,本文以船舶所有人的立场在考虑干散货二手船价尖峰厚尾的基础上,用GARCH-GED模型计算5年期好望角船型(CAPESIZE)干散货二手船价的波动率,以更好地解释数据的波动集聚性.首次同时采用VaR的测度方法对干散货二手船交易在一定置信水平下的损失和损失发生概率进行定量分析.用VaR模型对二手船交易在一定概率水平下的潜在损失进行测度,用ES模型计算损失超过阈值时可能遭受的平均潜在损失的大小,首次对二手船交易数据的尾部特征进行分析.上述方法不仅能够体现二手船价格序列的厚尾性,更能全面测度单个二手船交易和船队投资组合的交易风险,有效服务于二手船交易市场参与者.
1 基本模型
1.1 GARCH 模型
很多实证研究发现,部分类型的时间序列波动随时间变化,幅度较大的波动会相对集中在某些时段里,幅度较小的波动则会集中在另一些时段里,具有波动群聚性特征.波动群聚现象与厚尾现象密切相关,波动群聚现象在收益率的分布上往往表现出尖峰厚尾的特征.航运市场中许多序列存在此特性,如干散货运价[8]、运价指数[9]、原油运价[10]、干散货二手船价序列等,其误差项存在自相关性和条件异方差问题,BOLLERSLEV 提出的GARCH 模型可以较好地描述具有尖峰厚尾特性的序列,GARCH( p,q) 的数学描述[15]为
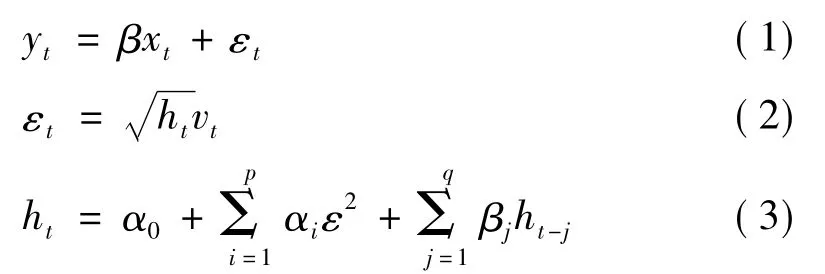
式中:前定解释变量xt可包括y的滞后值,β为参数;q≥0,p≥0,αi≥0,βi≥0.若则意味着GARCH过程是协方差平稳的.GARCH模型的条件方差不仅是滞后残差平方的线性函数,而且是滞后条件方差的线性函数,在计算量不大时,GARCH过程能方便描述高阶的ARCH过程,因而更具有适用性.
广义误差分布(GED)的最重要特征就是描述尾部的分布参数d,也即GED的自由度.通过对参数d的调整变化可以拟合不同的图形,处理不同程度的尖峰厚尾现象.本文引入GED刻画收益率序列的厚尾特征,其密度函数为
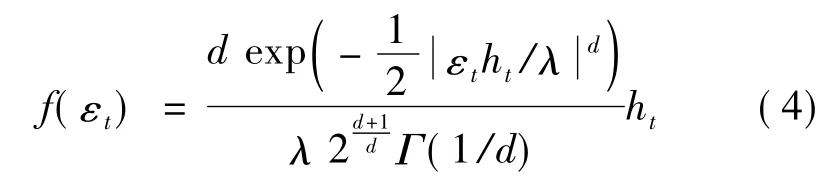
1.2 VaR 模型
VaR模型是指在一定概率水平(置信度)下,某一资产或资产组合的价值在未来特定一段时间内可能遭受的最大潜在损失.用公式[8]表示为
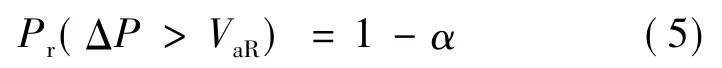
式中:Pr为资产价值损失额大于最大潜在损失的概率;ΔP为某资产在一定持有期Δt内的价值损失额;VaR为置信水平α下的风险价值(可能的损失上限),其中α为给定的概率(置信水平).
VaR实质上是一个统计估计量,故可以在不同的统计假设下运用不同的统计方法计算得到VaR值.考虑一项金融资产,设V0为其初始价值,r为收益率,μ为期望收益率,在给定置信水平α下,资产的最小价值为V*=V0(1+r*),其中r*表示最低收益率.此时VaR为资产的期望价值与最小价值之差[16],即VaR=E(V)-V*=-V0(r*-μ).若r服从均值和方差分别为μΔt和δ2Δt的正态分布,且假设连续时间区间内的收益率不相关,VaR的计算公式还可表述为
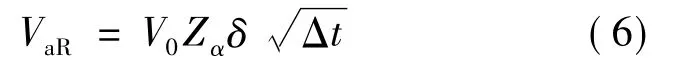
式中:Zα为相应置信水平下的标准正态分布的上分位数;δ表示收益率r的标准差;Δt为资产的持有期间.这种方法可以由正态分布推广到其他累积概率分布函数,所有的不确定性都体现在δ上.Zα的取值依赖于资产收益率的分布函数,不同分布下α对应的分位数也不同.
VaR的计算方法主要有3种,即方差—协方差法、历史模拟法和蒙特卡罗模拟法.针对市场的不稳定现象,方差—协方差法通过采用不同的分布形式,在一定程度上能解决VaR计算结果可能产生偏差的问题,本文采用这种方法分析二手船交易的价格风险,针对方差—协方差法在实际应用中普遍存在的如何描述金融数据序列的尖峰厚尾、群聚性、相关性和如何寻找金融数据序列的分布密度函数等问题,引入GARCH-GED波动性模型解决.
为了更好地应用VaR模型进行实际分析,本文还计算在不同置信度下VaR计算结果对实际损失的覆盖程度,选取样本期内所有交易日的VaR与第二月的实际二手船价变化值进行对比.计算溢出天数,若VaRt≥Pt- Pt+1;Et=1,若VaRt<Pt-Pt+1;e=E/T.其中,Pt表示时刻t的CAPESIZE二手船价,E表示VaR小于二手船价实际下降值的溢出天数,e为溢出率,T表示样本期的总天数.将e与显著性水平相比较,若e>1-α,表明在此置信水平下模型低估了风险;若e<1-α,则表明在此置信水平下模型预测结果已覆盖实际损失,随后选取预测结果好的置信度进行单月二手船价VaR的应用分析.
1.3 ES 模型
尽管VaR方法可以考虑在某个置信水平下的风险,但VaR本质上只是某个置信水平下的分位点,故又称为分位点VaR,因此它无法考察超过分位点的下方风险信息,即所谓的左尾风险,这就是VaR尾部损失测量的非充分性,它使人们忽略小概率发生时的巨额损失情形,而这些恰恰是金融风险所必须关注的.VaR尾部风险测量的非充分性是VaR固有的缺点,为了克服 VaR的不足,ROEKAFELLER和URYASEV提出条件风险价值CVaR,即ES的风险计量技术,被学术界认为是一种比VaR风险计量技术更为合理有效的现代风险管理方法,与VaR结合使用可以更加全面地量化风险.SE是指损失超过VaR的条件均值,也称为平均超额损失、预期尾部损失、平均短缺或尾部VaR,SE被定义为损失大于某个给定的VaR值条件下的期望损失,其数学表达式[17]为
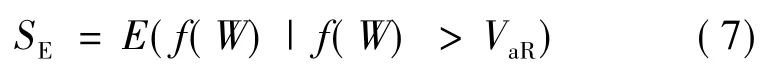
式中:f(W)表示损失(即负的收益);SE代表超额损失的平均水平,反映损失超过VaR阈值时可能遭受的平均潜在损失的大小,较之VaR更能体现潜在的风险价值.
评估VaR和SE的方法可以分为两大类:一类是线性规划方法;一类是根据参数法拟合出的收益率序列分布特征以及求出的VaR值,并求出相应分布和置信水平的条件分位数,然后求出SE值.本文采用后者,首先根据金融资产收益率序列的统计特性,在一定数学模型和分布假设下对序列整体进行拟合,再选取拟合效果好的模型计算得到波动率并求出VaR,然后计算出条件分位数,最后计算出SE.若用α表示对应于某一置信水平的分位数,用q表示大于α的分位数,根据广义误差分布的密度函数公式可推导出GED条件下的SE[17]为
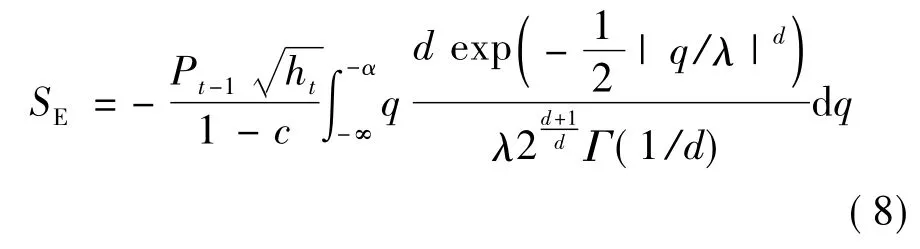
上述公式不容易求出其解析解,在具体应用时,本文采用Mathematics 5.0求出其数解.除此之外,还计算VaR损失值与SE的差别,采用下述检验统计量[17]对 SE进行返回检验,
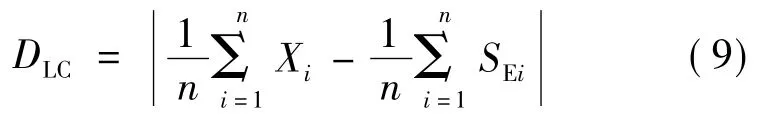
式中:DLC表示损失的期望值与SE之差的绝对值;X是超过VaR的实际损失;n是超过的个数.DLC越小,表示SE与实际损失的期望值越接近,SE估计得越好.
2 实证分析
2.1 样本选取及统计性描述
用CLARKSON中5年船龄的17万吨级的CAPESIZE二手船价格,数据范围从1986年5月至2011年3月.对二手船船价序列取自然对数ln C,可以压缩数量级使序列更加平稳,而且对数差分后对应的二手船价格可以被看成是价格变动率或二手船交易收益率.从图1可以看出,收益序列呈右偏性,峰度大于3,且JB统计量不服从正态分布,说明5年船龄的17万吨级的CAPESIZE二手船价格具有尖峰厚尾的特征.
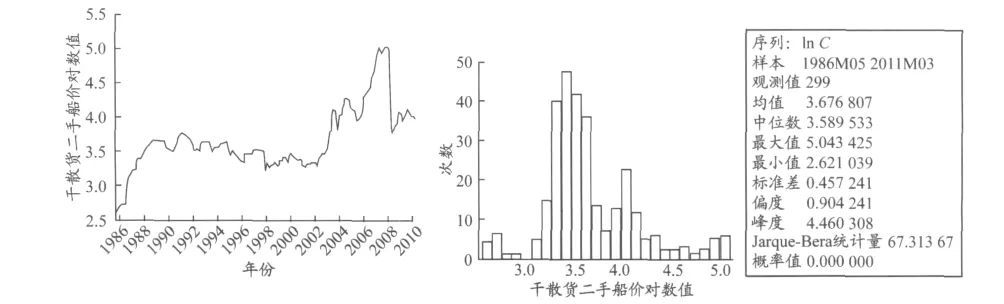
图1 描述性统计分布
2.2 模型建立
对序列ln C进行稳定性检验结果显示,该序列为一阶单整序列.通过事先假设ln C时间序列满足yt=yt-1+ εt(yt为该序列在 t时刻的取值),对模拟结果进行残差ARCH检验及模型修正,最后使用GARCH模型降阶.由于该时间序列具有厚尾性,为更好地描述其波动率,以更精确地进行后续的风险测量,最终建立GARCH-GED模型.表1所示模型的各项检验统计量良好,赤池信息准则、施瓦池信息准则和对数似然值的统计量和各系数检验统计量,前两个统计量较小,对数似然值的统计量较大,表示估计结果良好.

表1 GARCH-GED模型结果
对该模型残差独立性进行检验,Q统计量检验表明无法否定残差为白噪声序列,对该模型的残差进行ARCH效应检验,结果显示GARCH-GED模型残差序列不存在ARCH效应,模型可以描述如下:

2.3 VaR和ES模型计算及检验
2.3.1 CAPESIZE二手船交易VaR计算及应用分析
根据得到的GED的自由度v值为0.717 702,需要计算99%和95%置信度下的GED的分位数分别为2.972 8和 1.551 9.由于本文采用 GARCHGED模型的方差描述船价收益率序列的波动并计算VaR值,根据式(6)可将一般的计算单月VaR的模型变化为
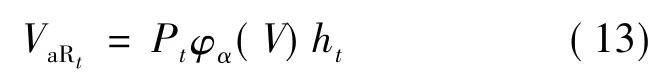
式中:Pt为第t月的船舶交易价;α为自由度v,置信水平α下GED的上分位数;ht为GARCH模型估计得到的ln C序列的第t月条件标准差.这样计算所得的VaR表示下一月船价可能下跌的最大值.为了保证精确性,还计算出样本期间每月的船价VaR.例如,2008年8月的CAPESIZE二手船价为153×106美元,在99%置信度下的VaR值为53.195 2×106美元,它表示下一月(9月)的船价有99%的可能性不会低于99.804 8(153-53.195 2) ×106美元.而实际上9月的CAPESIZE二手船船价为134×106美元.图2分别对比不同置信度下计算所得的单月船运价VaR值与实际船价变动的情况,此处的实际变动是指第二月船价与计算VaR当月的船价之差.

从图3可以看出:当置信度为99%时单日船价VaR大于95%置信度下的值,前者覆盖更多的实际船价变化值.进一步计算可得:当置信度为99%时,e=1/298=0.003 356,虽小于1-99% ,但是有些过小,模型略显保守;当置信度为95%时,e=20/298=0.067 114,大于1-95%,说明在此置信度下,模型会低估风险;相较两者,本文选取99%的置信度下对单月船价VaR进行应用分析,见图4.
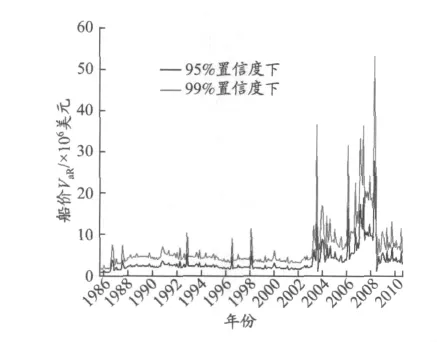
图3 95%和99%置信度下单月船价VaR比对
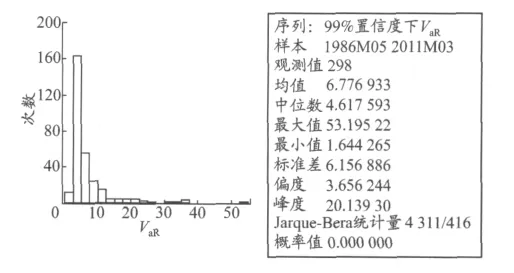
图4 99%置信度下单月船价VaR统计分析
由上图可知:CAPESIZE单月船价VaR的均值为6.776 693 3×106美元,最大值高达53.195 22 ×106美元,接近CAPESIZE 5年期二手船的平均价,凸显出二手船价的波动性和高风险性,最小值1.644 265×106美元;上述VaR值分析图呈非正态分布,说明船价风险的动态性及难预测性.
2.3.2 CAPESIZE二手船交易SE计算及后验测试
同样使用上文中计算得到的GED自由度v值为0.717 702,需要计算在99%和95%置信度下的GED的分位数分别为2.972 8和1.551 9.
使用SE计算公式所得在99%和95%置信度下的SE与上节中VaR对比见图5,SE的取值大于VaR,因此总体上说,SE是一种可以覆盖更大范围左尾风险的风险度量工具.

对SE的返回检验,还要关心VaR的违反值与SE的差别大小,因为SE在理论上表示超过VaR的均值.将文中计算出的SE和VaR代入计算,得出在99%置信度下 DLC=0.052,在 95%置信度下 DLC=0.069,在两种置信度下DLC的计算结果非常小,表示在两种置信度下SE估计结果均良好.
除此之外,还可以检验在VaR估计失效的交易日里,SE是否可以有效覆盖风险.表2列出在99%置信度下VaR估计失效的交易日里,实际损失、VaR及SE的均值,可以看出在VaR估计失效的交易日里,实际损失的平均值与SE的平均值很接近,说明当VaR估计失败时,SE对损失的估计比较准确,从而说明SE能够较准确地度量左尾风险.

表2 在VaR失效的交易日里实际损失与VaR和SE的比较
目前,在二手船交易市场,由于船舶价值远期合约(FoSVA)使用范围较小,基于二手船价格指数的衍生品尚未在实际中使用,在缺乏有效风险管理工具的背景下对二手船交易的风险进行量化显得更加重要;上述VaR和SE风险测度的实证分析说明其在二手船交易的风险量化的适用性,船舶所有人在进行船舶买卖决策时,可以通过VaR了解船价在极端市场下的跌幅(损失),还可以通过SE值得知在未来一段时间内跌幅扩大的的概率,船舶所有人可以结合自身的资金实力和风险喜好程度把握交易时机;部分实力雄厚的船舶所有人在船队管理过程中会对各种船型进行投资组合以分散风险(投资组合的风险应该小于或等于组合中各种资产分散计量的风险之和);基于上述实证结果,通过对船队投资组合中的各项资产风险进行方差和协方差的加权平均后,依然可以使用VaR和SE对投资组合进行风险量化.
3 结束语
通过构造建立GARCH-GED模型计算出好望角船型(CAPESIZE)干散货船价的波动率,并以此为基础采用VaR和ES两个模型对二手船交易的风险进行测度,实证结果显示上述测度方法有助于二手船交易的决策和风险测度,能有效描述单个或多个船舶组合资产的整体市场风险状况,且对其他船型的二手船交易风险测度具有示范作用.在上述研究的基础上,进一步的研究可以循着下述方向展开:引入分串法和极值指标处理二手船交易收益率序列的相关性和波动集聚性等研究二手船交易市场的流动性风险.
[1]李珩.船舶市场的规律性分析与发展研究[D].大连:大连海事大学,2007.
[2]KAVUSSANOS M G.The dynamics of time-varying volatilities in different size secondhand ship prices of the dry-cargo sector[J].Applied Econo,2001,29(4):433-443.
[3]MANOLIS G.KAVUSSANOS,AMIR H A.Efficient pricing of ships in the dry bulk sector of the shipping industry[J].Maritime Policy& Manage,1997,29(3):303-330.
[4]蔡立明,卢春霞.ARIMA模型在二手船价格预测中的应用[J].中国水运,2008,8(6):96-98.
[5]王辉.VaR方法在国际干散货航运市场风险测量中的应用研究[D].大连:大连海事大学,2007.
[6]马国强.基于VaR历史模拟法的干散货航运市场分析[D].上海:复旦大学,2010.
[7]于圆.VaR方法在海运行业金融衍生品交易中的应用研究[D].北京:北京邮电大学,2008.
[8]刘萍,赵一飞.基于风险价值模型的航运指数期货风险测度[J].上海海事大学学报,2010,31(2):80-83.
[9]翟海杰,李序颖.不同分布的GARCH族模型的波罗的海干散货运价指数波动率[J].上海海事大学学报,2009,30(3):59-64.
[10]王军,张丽娜.基于广义自回归条件异方差模型的世界原油运价风险分析[J].上海海事大学学报,2011,32(2):20-24.
[11]SYRIOPOULOS T,ROUMPIS E.Asset allocation and value at risk in shipping equity portfolios[J].Maritime Policy& Manage,2009,36(1):57-78.
[12]KAVUSSANOS M G,DIMITRIS N D.Market risk model selection and medium-term risk with limited data:application to ocean tanker freight markets[J].Int Rev of Financial Anal,2011,20(5):258-268.
[13]AMIR H A,NIKOS K N.Shipping derivatives and risk management[M].London:Faculty of Finance,Cass Business School,City Univ,2008:3-22.
[14]李云光.航运企业船舶投资风险研究[D].大连:大连海事大学,2009.
[15]易丹辉.数据分析与EViews应用[M].北京:中国统计出版社,2002:120-180.
[16]郑文通.金融风险管理的VaR方法及其应用[J].国际金融研究,1997(09):58-62.
[17]李坤.VaR与CVaR在金融风险测度中的应用[D].青岛:青岛大学,2006.

