集装箱班轮发船间隔时间动态博弈模型及其应用:以应对“天天马士基”为例
殷允健,赵刚
(上海海事大学交通运输学院,上海 201306)
0 引言
班轮发船间隔时间是指从一个班次的船舶驶离港口起,直至下一个班次的船舶再次驶离该港的时间间隔.传统集装箱班轮发船间隔时间的确定一般是先通过预测船公司在该航线的货运量,再结合自身的运力,经过一定的航次估算得来,这就存在如下两个问题:
(1)由于发船间隔时间的长短直接影响船公司的揽货数量,船公司在某条航线的货运量是受其发船间隔时间影响的.船公司先预测自身能够揽到的货运量,再确定发船间隔时间,显然不合理.
(2)在集装箱班轮运输这个竞争异常激烈的市场,处处隐藏着博弈与反博弈,因此船公司仅通过对航线货运量的预测以及自身运力的估计,却不考虑主要竞争对手的实力和战略,就确定发船间隔时间,显然难以达到利润最大化的目的.
目前,几乎没有对集装箱班轮发船间隔时间的研究,许多船公司都是凭着以往营运的经验排定班轮的班期,如何通过建立数学模型优化班轮的发船间隔时间,达到船公司利润最大化的目的就成为一个十分有意义的研究课题.
1 班轮发船间隔时间的基本概念
1.1 动态博弈的概念
博弈论可以分为合作博弈和非合作博弈.[1]非合作博弈强调的是个人理性、个人最优决策,其结果可能是有效率的,也可能是无效率的.
根据参与人决策的先后顺序,非合作博弈可以再分为静态博弈和动态博弈.[2]静态博弈指参与人在博弈中同时行动或虽非同时行动但后行动者并不知道先行动者采取的具体行动;动态博弈指的是参与人的行动有先后顺序,而且后行动者能够观察到先行动者所选择的行动.
本文中的班轮发船间隔时间优化模型建立在对手已作出战略决策之后(如已知对手发船间隔时间、航线配船数等信息)[3],通过调整自己的发船间隔时间,从而达到利益最大化的目的.因此,这种博弈方式属于动态博弈的范畴.
需要注明的是,采用动态博弈理论构建数学优化模型的目的并不在于打压竞争对手,而是在对手已作出决策的前提下通过调节自己的发船间隔时间实现自身利益最大化.本文采用对主要竞争对手(即一个竞争对手)的动态博弈建立模型,以求实现利益最大化这一目标.
1.2 有关班轮发船间隔时间的基本原理
班轮的发船间隔时间必须具有一定的规律性.计算所得的发船间隔时间须按规则要求加以调整.如果不规则,就会引起运行上的混乱,对货主和港口都有所不便,并影响船舶揽货和在港作业的效率,使船公司遭受不必要的经济损失.[4]
确定班轮的发船间隔时间,从而达到船公司的利益最大化,则需要考虑运费收入和运营成本两个因素.班轮发船间隔时间短一些,会揽到更多的货,从而得到更多的运费收入,这在运费较高的时期是可行的;而发船间隔时间长一些,揽到的货就会减少,但是相应的船舶运营成本也会下降,这通常是运费较低时期船公司可能采取的经营策略.
因此,根据竞争对手的发船间隔时间、一定时期内的平均运价,再结合运费收入和运营成本两个因素,通过建立数学模型求解得到的发船间隔时间将会给船公司带来最大的利益.
2 班轮发船间隔时间优化模型的建立
建立班轮发船间隔时间优化模型是为了让船公司在一定时期内通过调整发船间隔时间获得最大利益.本文以1 a为计数期,针对一个主要竞争对手通过动态博弈构建班轮发船间隔时间数学模型.主要竞争对手是指对船公司本身构成直接竞争的对手,如挂靠港和航线基本相同的船公司.为方便起见,设主要竞争对手为C1,自己的船公司为C2.
2.1 运费收入因素
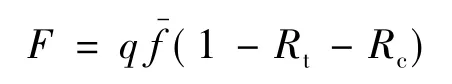
需要指出的是,船公司揽货的数量并不完全与发船间隔时间有关,这是因为一部分货主与船公司在年前已经签订运输合同、不同船公司服务质量不同、货主偏好某些船公司等.因此,有一部分货物q固是不受发船间隔时间影响的,设q固占总运量q的比重为ρ(0<ρ<1),受班轮发船间隔时间影响而浮动的货物为q动,则
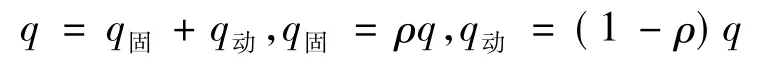
设某条航线上C1和C2的货运量总数为Q,也可以将Q划分为Q固和Q动,可以通过C1和C2所占航线的市场份额和运力比重适当估算得出Q.
设C1在某条航线的历年市场份额为e1,发船间隔时间为t间1;C2的历年市场份额为e2,发船间隔时间为 t间2.
由于业内没有关于发船间隔时间对浮动货物数量q动具体影响的函数和公式,假设q动与发船的频率成正比,则C2受发船间隔时间影响的货运量,化简可得
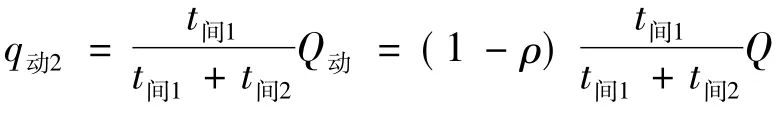
因此,C21 a的揽货数量
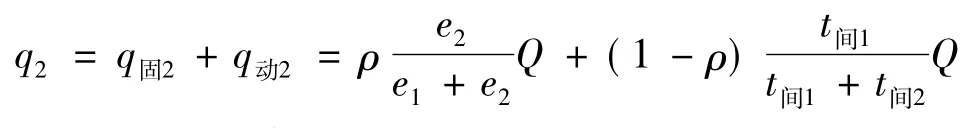
此时,C2在一条航线上1 a的运费收入
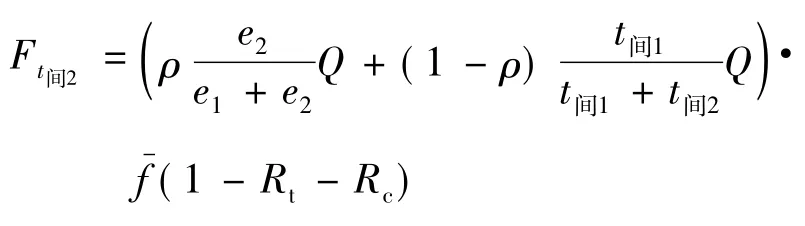
2.2 运营成本因素
影响集装箱班轮运营成本的主要因素有船员工资及福利,船舶保险费,船舶修理费,管理费,燃料费,润料、物料费,港口使费,船舶折旧费[5],装卸费[6]等.为方便计算,以上费用除了装卸费外,都按年均每艘船舶所需费用计算.
K1为年均每艘船舶配备船员的工资、福利;K2为年均每艘船舶保险费;K3为年均每艘船舶修理费;K4为年均每艘船舶管理费;K5为年均每艘船舶燃料费;K6为年均每艘船舶润料、物料费;K7为年均每艘船舶港口使费;K8为年均每艘船舶折旧费.
由于集装箱船装卸费用主要受货物数量的影响,因此装卸费
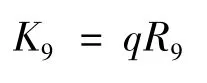
式中:q为年货运量,TEU;R9为平均每标准箱货物的装卸费率,USD/TEU.因此,要计算C21 a的运营成本费用,只需要知道航线所需船舶数和年货运量q2即可.
设往返航次时间为 t往返,则航线配船数 m=,而q2为,则C21 a的运营成本费用

由运费收入 Ft间2以及运营成本 Kt间2,可得出年收益,即
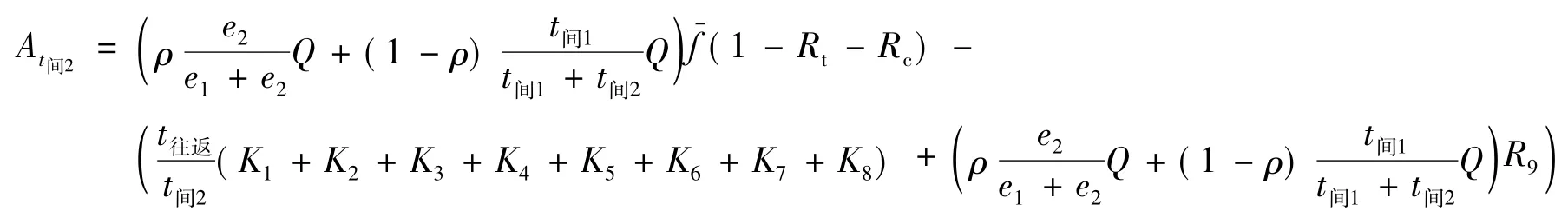
求得 max At间2就是 C2的目标.
2.3 模型的约束条件
班轮发船间隔时间优化模型主要需考虑以下3个约束条件.
(1)发船间隔时间,即 t间2的取值.首先,t间2必须是整数,且最好是 5 d,7 d 的整数倍.其次,t间2不宜过长,一般不超过1个月.
(2)船公司单方向的运力应满足最大单方向货运量需求.
因为要考虑运输方向不平衡系数,船公司所提供的运力(Y)至少为最大单方向货运量的2倍.不妨设最大单方向货运量为q大,则约束条件可表示为

(3)航线配船数应小于船公司的最大供给能力,即
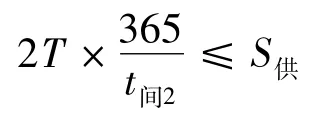
2.4 模型的求解
综上所述,可得目标函数:
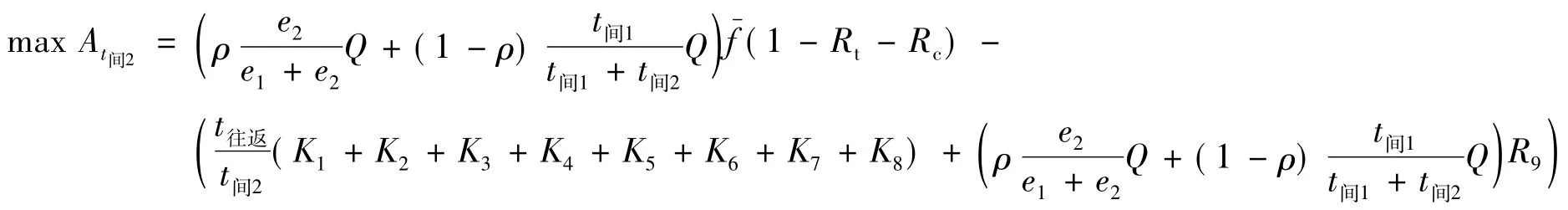
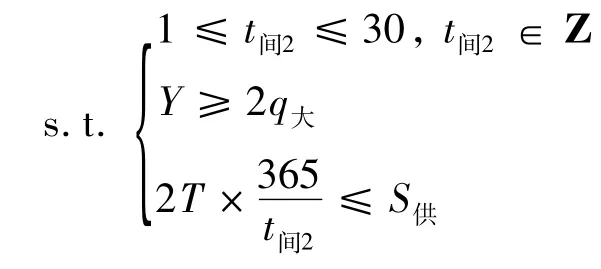
此模型建立在动态博弈的基础之上,因此对手C1的发船间隔时间t间1为已知,而其余相关参数(如年平均运价、燃油价格、船员工资、每标准箱装卸费等)均可凭借历年经营管理的经验估算得到,目标函数只有t间2未知,此时求解模型只要在满足约束条件的基础上,运用高等数学中的求导法求解.具体求解步骤如下:

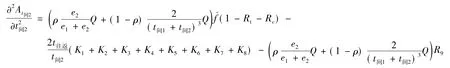
(3)最后,根据求得的 t′间2,代入原函数,解得最大值即可.此时 max A′t间2的含义为:在对手 C1的发船间隔为 t间1时,C2若选择 t′间2作为发船间隔时间,将可为自身带来最大利益(利润).
3 班轮发船间隔时间模型的应用
3.1 马士基航运与地中海—达飞联盟
为改革现有班轮运输船舶准班率及揽货模式,丹麦马士基航运日前在全行业率先公布一项崭新的服务项目与内容,将之命名为“日班—马士基”,即“天天马士基”.“天天马士基”计划在短期内于亚欧航线上推出每日一班由中国港口始发的航班,特点是只收正价、不设附加费,沿途只挂亚欧7个港口,每周7 d均设同一截关/截港时间.全航线准备投入70艘8 000~15 000 TEU集装箱船循环使用.[7]
在亚欧航线上,市场占有率前3位的依次为马士基、地中海、达飞,因此马士基的这一举动对地中海和达飞形成强有力的挑战和竞争.为了应对马士基航运咄咄逼人的态势,地中海航运和达飞航运于2011年12月正式结盟.
3.2 运费收入及运营成本指标的估算
现可将马士基航运与地中海—达飞联盟视为动态博弈的两个对手.不妨设C1为马士基航运,C2为地中海—达飞联盟.结合2012年C1和C2在亚欧航线投入的船型,设C1的班轮均为10 000 TEU型船,C2的班轮均为13 000 TEU型船.
在C1确定t间1=1 d,航线配船数为70艘的情况下(可得t往返=70 d),C2再估算运费收入及运营成本,并结合 C1确定的 t间1确定 t间2,并实现2012年的max At间2.以下是关于运价和运营成本的估算.
(1)运费收入相关参数的估算.由于2012年亚欧航线各班轮公司纷纷提价,导致运价有所上升,结合2012年上半年亚欧航线东西向运价实际情况及对未来趋势的预估,这里取=1 200美元/TEU,Rt=3%,Rc=1.5%.
(2)运营成本相关参数的估算.年均每艘船舶配备船员(30人)的 K1=30×10 000美元/月 =3.6×106美元/a;年均每艘 K2=1 ×106美元[8];年均每艘 K3=0.5×106美元;年均每艘 K4=0.5×106美元;年均每艘K5=365R5r,式中:r为航行天数占全年天数比重,这里取0.8;R5为日均船舶耗油成本,美元/d.R5主要受船型、航行速度及船用燃油价格影响,而在运价低迷的航运市场,目前各船公司普遍采用较低航速(约20 kn).根据新加坡港2012年第一、第二季度几种船用油的价格,这里估算燃油价格取值为850美元/t.据Germanischer Lloyd统计,在燃油价格为450美元/t时,13 000 TEU型船在航速20 kn下每天的燃料费约为48 700美元[9],根据换算求得美元/d,故K5=2.69×107美元;年均每艘K6=30×500美元/月=18×104美元/a;年均每艘K7=1.78×107美元(此数值根据船舶吨位和国际港口使费[10]征收标准估算求得);年均每艘美元 /a,式中:P为船舶资产的原值,L为船舶资产的残值,N为船舶资产的折旧年限;1 a的装卸费 K9=取 300 美元/TEU.
(3)航线货运量的估算.首先需要指出的是,这是对航线货运量的估算,而不是对C1和C2分别能揽到货物量的估算,因为C1和C2能具体揽到的货量还与它们的发船间隔时间有关,只能用航线货运量 Q,t间1和 t间2的数学表达式表示.据业内人士估计,2012年亚欧航线C1的市场份额e1约为26%,C2的市场份额e2约为22%.2011年亚欧航线东西向的集装箱货运量分别为4.17×106TEU和9.19×106TEU,预测2012年运量的增长率为8%,故2012年亚欧航线东西向的货运量分别为4.5×106TEU和9.93×106TEU.结合C1和C2的市场份额,得出C1和C2共有的东西向货运量分别为2.16×106TEU和4.76×106TEU,年货运总量 Q 约为6.92×106TEU.
3.3 模型求解
影响ρ的因素很多,包括合同的签订、船公司声誉、服务水平等,这里取ρ=0.25,即100箱货物中有25箱是不受发船间隔时间影响的.于是,将所有参数值代入
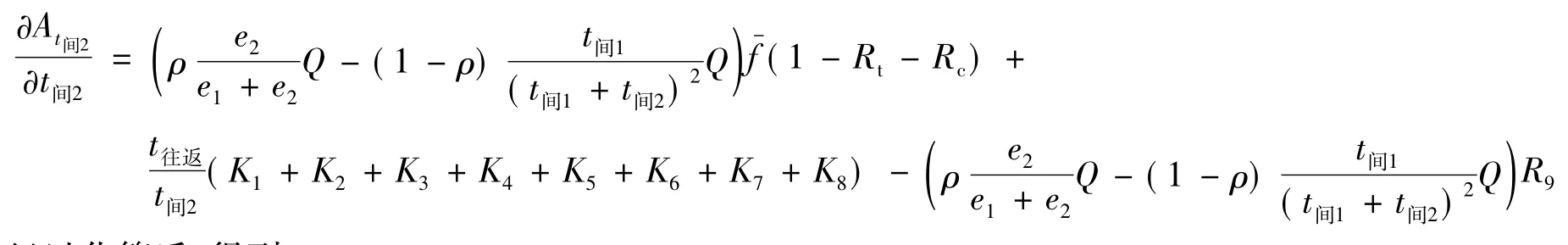
经过化简后,得到

因为t间2为[1,30]的正整数,所以恒大于0,则一阶导恒大于 0,故 C2的年利润 At间2随 t间2单调递增,但t间2还必须满足约束条件

当t间2取值为5d时,C21a能够提供的运力为1.9×106TEU,小于C2西行方向所揽到货运量的2倍(2.28×106TEU),运力不足,不满足约束条件;当t间2取值为4d时,C21 a能够提供的运力为2.39×106TEU,小于C2西行方向所揽到的货运量的2倍(2.52×106TEU),运力不足,不满足约束条件;当t间2取值为3d时,C21a能够提供的运力为3.17×106TEU,大于C2西行方向所揽到的货运量的2倍(2.88×106TEU),满足约束条件.因此,t间2=3 d,代入目标函数,可求得运费收入 F3d为23.96亿美元,运营成本 K3d为 19.25亿美元,则max A3d为 4.71 亿美元.
C1与C2运营对比见表1.
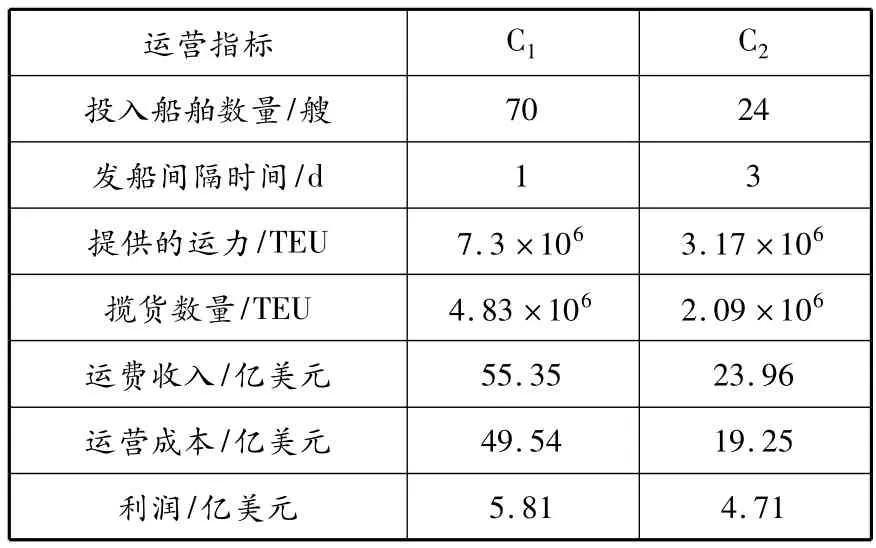
表1 C1与C2运营对比
由表1可得,当运价逐步回归合理水平时,“天天马士基”为赢利状态;而地中海—达飞联盟通过动态博弈,合理配置船队规模,确定最优发船间隔时间,在激烈的航运市场得到令人满意的结果.虽然地中海—达飞联盟在总赢利方面略逊于马士基航运,但在投入产出比方面,却远超马士基航运.但需要指出的是,航运市场瞬息万变,且马士基航运这种打压竞争对手的战略从某种角度看有其强大的“杀伤力”,而“天天马士基”效果到底如何,还有待市场的进一步检验.
4 结束语
通过对主要竞争对手发船间隔时间的动态博弈,结合运费和成本等因素,确定自身的最佳发船间隔时间,无疑将给船公司带来最大的经济利益.而这也改变了传统班轮确定发船间隔时间的理念,为班轮公司提供更多的选择.因此,通过动态博弈建立模型的方式确定发船间隔时间对船公司意义重大.
但是,关于发船间隔时间的研究极少,且班轮公司的一些运营成本数据也难以搜集,本文提出的关于集装箱班轮发船间隔时间动态博弈模型仅供参考.相关因素,如航线货运量、运输方向不平衡系数、多个竞争对手的博弈、不受班轮发船间隔时间影响的货物比重等,有待进一步研究和完善.
[1]GANJI A,KHALILI D,KARAMOUZ M,et al.A fuzzy stochastic dynamic Nash game analysis of policies for managing water allocation in a reservoir system[J].Water Resour Manage,2008,22(1):52-53.
[2]张艳奎.集装箱班轮运输战略联盟[D].上海:上海海事大学,2004:13-14.
[3]张颖菁,刘娟娟.基于博弈模型的绿色物流税收策略[J].上海海事大学学报,2010,31(1):53-54.
[4]赵刚,李玉如,顾伟红.国际航运管理[M].大连:大连海事大学出版社,2006:205-206.
[5]邵瑞庆.交通运输业固定资产会计的若干问题[J].上海海事大学学报,2006,27(1):63-65.
[6]赵刚,陈舜.面向市场随机需求的船舶生产计划与调度优化理论及应用研究[C]//第四届亚太可持续发展交通与环境技术大会论文集.西安:2005:676-678.
[7]杨川梅.“天天马士基”竖起航运业新坐标[N].中国经济导报,2011-09-29.
[8]李希平.船舶保险与船舶保赔保险若干问题之比较研究[D].上海:上海海运学院,2002:7-8.
[9]陈羽.高燃油成本对集装箱船耗油管理的影响[J].集装箱化,2008,19(12):18-21.
[10]沈解民.港口使费控制的策略研究[J].港口科技,2008(9):37-38.

