格基规约算法研究进展
周世祥,刘梁华
(1.山东理工大学理学院,山东淄博255091;2.山东淄博实验中学,山东淄博255091)
1 预备知识
格出现在19世纪的数论和密码研究中,很长一段时间,格在密码学中的应用主要是负面的,常被用来破解各种密码方案,可喜的是,过去10年中已出现过好几个积极的应用,人们已经设计了一些基于格困难问题的密码系统.基于格密码学的非凡特性是它们可证明安全(即平均上难于破解).格问题已被密码学界建议为新的计算困难问题的源泉,用于构造可证明安全密码函数.
设b1,…,bd是n维欧式空间Rn中线性无关的实向量,定义点集

为格,称b1,…,bd为格的一个基.因为b1,…bd是线性无关的,任何格矢量x可用基线性组合表示,且表达的方式也应该是唯一的(λ1,…,λd唯一);反之,如果x在格中且能用上述实线性组合形式表示,则系数λ1,…,λd一定为整数.
每一个格矢量都可以唯一地表示为基矢量的整线性组合.用基表示格是有意义的,格基自身就可以用一个实系数矩阵表示,这样一来人们可以很方便地利用计算机来表示某个格.
从代数的角度看,格是具有d个生成元的Abel群,被认为是Rn的子群.格矢量在“加”的意义下形成群,如果a∈L,则-a∈L,如果a,b∈L,则a±b∈L,所以格是最普通的n维空间上的离散加子群.格的任何子群也是格.
格计算研究的中心问题是Shortest Vector Problem(SVP):给定一个格基B,找到一个非零格矢量Bx≠0,长度达到最小值‖Bx‖=λ1,这里长度可被定义成关于任何范数,但欧几里得l2范数是最常用的.
另一个问题是Closest Vector Problem(CVP).给定一个目标矢量和格基,要求找到最靠近该矢量的格点.CVP问题比SVP问题稍难.精确的SVP是NP难的,实际中也不一定需要,所以有人提出了下面的近似SVP问题.
给定一个秩为d的格L基B,一个近似因子γ≥1,找到非零矢量u∈L,使得‖u‖这个问题称为近似SVP问题,简记作apprSVP.目前,已证明对于近似因子γ=的apprSVP问题是NP难的.
没有有效的算法找任意格中最短矢量,1981年van Emde Boas证明:确定一个给定的格元素是否是l∞最短的是NP完全问题.Ajtai证明在随机规约下,找欧几里得范数下最短矢量问题是NP难的,Micciancio证实在近似因子小于时SVP问题也是NP难的.
下面给出一些与格基规约相关的概念.
对任何矢量集S⊆Rn,span(S)表示由S张成的线性空间,或者为Rn包含S的最小子空间.
设b1,…,bd∈Rn为格L的一个格基,则其Gram行列式,表示为△(b1,…,bd)是d×n阶Gram矩阵
Gram行列式有一个非常重要的几何解释:当b1,…,bd线性无关时,由矢量b1,…,bd所张成的平行多面体表示为

设Bn(0,r)={x∈Rn:‖x‖<r}表示中心在原点,半径为r的n维开球,简记为B(0,r).
对于子空间E⊂Rn,它的正交补表示为E⊥={x∈Rn:〈x,y〉=0,∀y∈E}.用:Rn→Rn表示向量到E⊥上的投影,则有,当x∈E⊥时,πE(x)=x,当x∈E时(x)=0.
设L⊂Rn是一个格,则L的秩定义为span(L)的维数,如果n=d,则格称为满秩的.
与Rn的线性子空间一样,格的基也是不唯一的.但最大不同的是,并非所有最大线性无关矢量集就能形成一个基.
每一个格有无限多个格基.设b1,…,bd∈Rn为格L的一个格基,矩阵表示为B,任何d个格矢量c1,…,cd∈L,矩阵表示为C,若存在一个可逆矩阵U,使得,C=BU,且|U|=±1,则c1,…,cd也是格L的一个基.显然满足要求的矩阵U有无限多个.
设M⊂L是L的子格,如果存在线性子空间E⊆Rn,使得M=L∩E,则称M为L的本原子群.容易证明M为本原子格的充要条件是M的每一个基都可以扩展为L的一个基.
类似地,定义本原格矢量b1,…,bk∈Rn,k<d,要求这组矢量能扩充为L的一个基b1,…,bd.
当投影一个格到它的子空间上时,可以得到投影格.设L⊂Rn是一个秩为d的格,M⊂L是L的秩为r的本原子格,1≤r≤d,定义:=为到span(M)的正交补空间上的投影,则πM(L)⊂Rn是一个秩为d-r的格.
设b1,…,bd∈Rn为格L的一个格基,b1,…,bi-1,i≤d是本原的,对于1≤i≤d,定义映射πi:=πspan({b1,…,bi-1}),则(L)是秩为d-i+1的格,从而减少了格L的秩,在格基规约的许多迭代算法中就是反复运用这个变换技巧来降低格的规模.
对任何秩为d的格L来说逐次最小值λ1,…,λd也是它的基本不变量.
正如前面所讲的SVP问题,每一个格一定存在最短非零矢量(不是唯一的),Minkowski定义了最短非零矢量的长度为格L的第一最小值λ1.然而,定义第二短矢量没有意义,所以Minkowski在他的逐次最短矢量定义中限定为线性无关的格矢量.
定义1 [逐次最小值(The successive minima)] 格L(b1,…,bd)的第i个逐次最小值λi,1≤i≤d定义为中心在原点,包含i个线性无关格矢量的最小球半径λi(L)=inf{r:dim(span(L∩B(0,r)))≥i}.
格作为离散子群,总存在矢量达到逐次最小值,即有线性无关的矢量x1,…,xd∈L使‖xi‖=λi,(i=1,…,d).然而,一旦dim(L)≥4,这样的矢量不一定形成一个格基.容易证明,任何两个不同格点之间的最小距离也等于最短非零格矢量的长度,λ1=min{‖x-y‖,xy∈L}.
早在19世纪Korkine和Zolotarev研究二次型时发现当格秩d≥5时,格L没有基能同时到达所有逐次最小值.
我们可以证明格L最短矢量长度λ1与它的体积vol(L)之间是齐次关系,因为如果用tL代替L,则λ1(tL)=|t|λ1(L),vol(tL)=.Hermite在研究二次型理论时,得出λ1(L)2/vol(L)2/d上边界为Hermite常量γd,即λ1(L)≤.然而,找到精确的γd也不是容易的事情,目前人们仅仅知道1≤d≤8及d=24时精确的γd值.Hermite自己证明了对于d≥2,γd≤其中,γ2=利用鸽笼原理,Minkowski证明了定理1.
定理1 (Minkowski凸体定理)设L⊂Rn是一个n秩格,C⊂Rn是其可测凸集,关于原点对称,且测度严格大于2nvol(L),则C∩L至少包含一个非零矢量.
根据定理1我们做出下列推论.
推论1 设L⊂Rn是一个d秩格,vd=为相应的单位球体积,其中Gamma函数可以看做阶乘函数在实数情况下的扩展,则格L包含一个非零矢量x,使得λ1(L)≤‖x‖≤
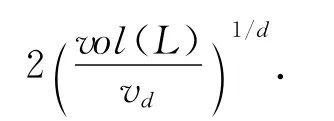
重写表达式为λ1(L)2/vol(L)2/d≤4/所以γd≤4/,我们得出γd的线性边界γd≤1.这个值可以帮助我们界定λ(L)的上边界.1
接下来考查λ2的范围,不幸的是对于λ2却无法界定.下面由一个实例可说明,设L是由矩阵生成的格,对于ε≤1,λ1(L)=ε,λ2(L)=1/ε,当ε→0时,λ2可以任意大.尽管如此,Minkowski从几何意义上整体界定了其他逐次最小值.
定理2 (Minkowski第二定理)设L⊂Rn是一个d秩格,则对1≤γ≤d,总有
对于基为b1,…,bd的格L总有Vol(L0)≤‖.当基矢量相互正交时,结果取等号.
定义2 (正交亏损orthogonality defect)基为b1,…,bd的格L正交亏损定义为‖/vol(L)≥1,等号成立条件是格基为正交基.
格基规约的目标是找到规约基,即由相当短或几乎正交的矢量组成的基.格基规约算法在计算机和数学的许多领域具有很高的价值[1].
2 规约基的定义和性质
1982年三位数学家伦斯特拉(A.k.Lenstra),伦斯特拉(H.W.Lenstra),洛伐兹(Jr.L.Lovász)发明了LLL算法.LLL算法被许多专家视为有关NP问题的一大突破,因为它简明性和广泛的应用,立即被认为是20世纪最重要的算法成果之一.
线性代数的基本理论表明任何有限维欧氏空间都有一个标准正交基,即一个基由两两正交的单位矢量组成,自然要问,格是否也有标准正交基,不幸的是,即使是对2维格,也可能没有正交基.格基规约的目标退而求其次,一个格总有一个基离正交不远,要精确定义何为离正交不远也是需要技巧的,迄今为止,仅仅可说这样一个基应当是由足够短的格矢量组成,意味着几何上这样的矢量离相互正交不远.下面给出规约基的一些精确定义.
2.1 规约基定义
从数学的观点看,规约的历史回溯到由lagrage,Gauss,Hermite等提出的二次型规约理论、由Minkowski开创的数的几何、以及1981年Lenstra的在整数线性规划上做出的令人赞美的工作.1982年Lovász受启发提出著名的LLL算法.这些算法在数学和计算机科学许多领域有着丰富的应用.
在规约理论中常用到克拉姆-施密特正交化GSO(Gram-Schmidt Orthogonalization).GSO广泛用于格基规约,关键在于它允许三角化基.设Rn是n维实矢量空间,有标准内积〈x,y〉=xty,一个矢量b∈Rn,有长度‖b‖=,一个线性无关的有序矢量集b1,…,bd∈Rn是维数dim(L)=d的格L⊂Rn的一个基,通常用矩阵B=[b1,…,bd] ∈Rn×d表示基,记L=L(B)=L(b1,…,bd),所有矢量为矩阵列向量形式.设qi表示bi正交于的b1,…,bi-1分量,q1=b1.基b1,…,bd的正交化矢量为q1,…,qd∈Rn,且Gram-Schmidt系数为,1≤i,j≤d,对j=1,…,d满足

设有格基b1,…,bd∈Zn,基长度上边界为M,不用快速整数算术,可以在O(d5log2M)时间内计算出GSO系数,即有理数μi,j,‖
基的几何标准型Geometric normal form(GNF).基B∈有唯一的分解B=QR,其中,Q∈Rn×d有两两正交的长度为1的列,且R=∈Rd×d是对角元为正的上三角矩阵,即i>j,=0,r1,1,…,rd,d>0,因此,
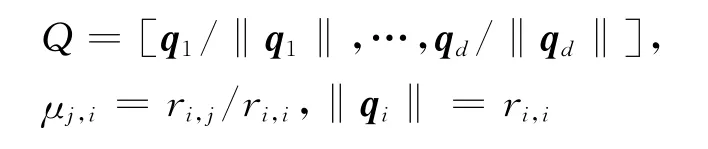
称R为基的几何标准型(GNF),记GNF(B)=R.通过二次型的研究,Hermite最早引进了弱规约的概念.
定义3 [Hermite大小规约] 格L的一个基b1,…,bd是大小规约的,如果它的GSO系数对所有的1≤j<i≤d,满足|μ,|≤.几何上,这意味着b
iji
在b1,…,bi-1线性张空间上投影bi-qi是在平行多面体P=|xj|≤1/2}内部,规约时我们总是试图减少bi在b1,…,bi-1线性张空间上的分量.定义也意味着对所有的1≤i≤d:‖≤
Lagrange在研究二次型时提出了下列规约概念.
定义4 [Lagrange规约] 设L⊂Rn是一个2秩格,基为b1,b2,如果‖b1‖≤‖b2‖,且〈b1,b2〉≤‖b1‖2/2,则基为Lagrange规约的.
定理3 设L⊂Rn是一个2秩格,基b1,b2是Lagrange规约的,则‖b1‖=λ1(L),‖b2‖=λ2(L).
LLL规约提出就是受到Lagrange规约的启发.
定义5 [Minkowski规约定义] 设格L的有序基B=[b1,…,bd] ,如果对所有的1≤i≤d,在所有的按序排列的第i个格矢量中bi有最小的范数,使得[b1,…,bi] 可以扩展成格L的一个基.
定义6 [Minkowski规约等价定义[2]] 设格L的有序基B=[b1,…,bd] ,如果对i∈[1,d] ,对任何整数x1,…,xd,使得xi,…,xd互素时,有‖x1b1+…+xdbd‖≥‖bi‖.
按上述定义,在低维时只需检验一些条件子集.一般地,要确定给定的基是Minkowski规约的需要验证无数个条件.这种规约主要用在数的几何理论上,因为不清楚是否有多项式时间算法计算这样的基,所以实际计算价值较小.
Korkine和Zolotarev进一步加强了Hermite的大小规约,即Hermite-Korkin-Zolotarev-reduction,简称HKZ-reduced:
定义7 [KZ(或HKZ)规约基递归定义[3]]
设格L的基B=[b1,…,bd] ,[q1,…,qd] 为其Gram-schmidt正交化矢量,L(d-1)表示L到Rb1=span(b1)的正交补上的投影,则KZ规约基满足下列三个条件:
1)b1是格的最短非零矢量.
2)Gram-schmidt系数|μ,|≤≤i≤d.
i1
3)b2,…,bd到的投影,b2-μ2,1b1,…,bd-μd,1b1是格L(d-1)的KZ基.
定义8 [KZ规约基非递归定义] 设格L的基B=[b1,…,bd] ,L(d-1)表示L到Rb1=span(b1)的正交补上的投影,则KZ规约基满足下列三个条件:
1)对于1≤i≤d来说,qi是格L(d-i+1)的最短非零矢量.
2)Gram-schmidt系数
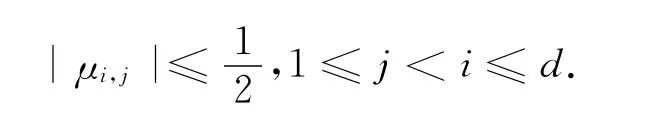
通过对任意二次型规约的研究,KZ及Minkowski考虑格基b1,…bd中b1是一个格最短非零矢量.Minkowski推广这个特性到所有的子基上,即bi是子格bi,…,bd的最短非零格矢量.KZ进一步推广,要求子基bi,…,bd在线性空间上的正交投影也有这个特性成立.
定义9 [分块k规约基] 如果对i=1,…,d-k+1,bi,…,bi+k-1在上的投影形成秩为k的KZ规约基,则称格基b1,…,bd为分块k规约的.
注意到qi∈πi(L)且qi0,自然要求‖qi‖=λ1(∏i(L)),特别地,条件‖qd‖=也是必然满足的.
这样的k规约基是局部KZ规约的.对k=2,概念上基本等价于LLL规约,对于d=k=2,与Gauss规约一致;对于d=k,就是KZ规约.
对i=0,…,m-2,如果对所有2k个分块bik+1,…,b(i+2)k的投影是KZ规约的,称格基b1,…,bmk是2k规约的.
每个分块2k规约基b1,…,bd包含一个近似因子为的最短格矢量.
为获得多项式时间算法,schnorr[4]放松规约概念,提出准k规约基和准分块2k规约基概念及算法.
2.2 KZ规约基和逐次最小值关系
设[b1,…,bn] 是格L的KZ规约基,λi(L),λi(L*)分别表示L和其对偶格L*的逐次最小值,Lagarias等1989年在文献[3]中证明对所有的1≤i≤n总有,[4/(i+3)] λi(L)2≤‖≤[(i+,且≤[(i+3)/4] [(n-i+4)/4,其中=min{γj:1≤j≤n},γj表示Hermite常量.
KZ规约基有两个有趣的特性.第一,KZ规约基是逐次最小值的很好近似.

第二,HKZ规约基有局部特性.从它的递归定义中就能看出这一点,如果(b1,…,bd)是KZ规约的,则对所有的1≤i≤j≤是HKZ规约的.这样通过研究低维KZ规约,可以递归得出任意维的特性.
3 规约算法目前的进展
第一个SVP算法是Lagrange的规约算法,在二次时间内解精确的二维SVP.对任意维格,有两类SVP算法.
3.1 精确算法
这些算法可证明找到一个最短矢量,但他们是开销很大,运行时间至少是维数的指数次.本质上,这些算法执行一个穷举搜索.精确算法可分成两类:
(1)多项式空间精确算法.这些算法基于列举法,下面我们简要阐述列举法的基本原理.列举法与基的GSO关系密切,设(b1,…,bd)为格L基,相应的GSO为(q1,…,qd),设u∈L是一个最短非零格矢量,M为一个设定的边界值,比如设为M=‖b1‖,此时有这样就把u表示为GramSchmidt-正交化矢量的和,u的投影也容易表示为由于正交性故有‖u‖2≤M2,这些不等式限制了λd,…,λ1搜索范围,可以找出所有长度小于M的非零格矢量.最好的确定性的列举算法是Kannan的算法[5],具有超指数的最坏复杂度多项式时间运算[6].

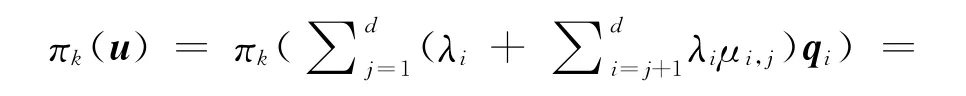

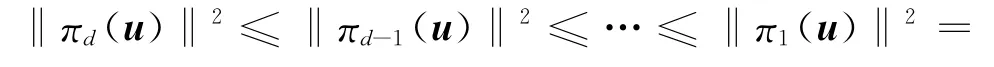
Schnorr引入的“剪枝”(Pruning)技巧[7],把列举法和分块规约结合起来,本质上是在分块KZ规约算法中利用列举算法作为一个子过程,算法获得一个很好的加速.
(2)指数空间精确算法.这些算法有更好的渐近运行时间,但它们都需要指数空间2Θ(n)存贮.这类算法的代表是Ajtai,Kumar,Sivakumar的随机筛法(简记AKS)[8],最坏情况下具有指数时间复杂度2O(n).最近Micciancio等提出一个确定性算法[9],能在多项式时间22n+O(n)内解CVP和SVP问题.有趣的是有好几个AKS的启发式变形[10-12],具有运行时间2O(n).
3.2 近似算法
这些算法比精确算法更快,但他们仅仅输出一个短格矢量,不一定是最短的.算法一般输出整个规约基,称之为格基规约算法,这类算法最著名的当属Lenstra,Lenstra and Lovász开发的LLL算法[13],算法可在多项式时间内解决近似因子为O((2/)的SVP问题,该算法可看作是Hermite不等式的算法版本.对LLL及其应用的全面总结见LLL的25周年会议文集[1],其中有两章描述了对LLL算法的改进.随着LLL出现,研究主要集中在两个方面:
(1)更快的LLL.获得质量类似于或弱一些的LLL规约基,但用更少的运行时间,技巧是通过分治策略,例如文献[14] .或通过浮点算法,当用浮点数算术可以加快格基规约速度,但同时也会带来浮点误差,这些误差会引起错误的结果,甚至使得程序不能终止,因此,研究格基规约上的浮点运算特性很有必要.第一个正确性得到证明的浮点LLL是由Schnorr于提出的[15],最近,一个更有效的浮点LLL改进由Nguyen和Stehlé提出的[7].目前,最流行的版本是启发式的浮点LLL.尽管常规方法有可证明的安全性,但有时启发式的方法更有效.一个重要的启发式方法是由Schnorr和Euchner于1994年提出的[7],直到今天这个算法仍然是许多浮点LLL快速算法的基础.有关浮点数的运算请参考[16].
(2)更强的LLL.用更多的运行时间获得比LLL更好的近似因子.分块规约方法(定义9)是在LLL规约和HKZ规约之间取一个折中方案,当分块长为d,参数δ=1,分块KZ规约等价于HKZ规约,当分块长为2时,分块KZ规约就是LLL规约.直觉地,LLL反复地用2维规约找到n维格的近似最短格矢量.用稍高维的精确规约子过程代替2维规约,分块规约算法[4]获得比LLL更好的近似因子.最好的多项式时间分块规约算法[17]目前达到一个亚指数近似因子.这个算法是Mordell不等式的算法版本.文献[7] 中也引进了“深插入(deep insertion)”的技巧,当Lovász条件不满足时,用深插入方法代替原LLL算法中交换步骤,即不交换bk-1和bk,而是把bk插入某个位置i,其中1≤i≤k-1,为寻找i,因为=qi长度相当,i从1开始,直到δqi>(bk)(δ为参数)为止,这时基b1,…,bk,…,bd重排为b1,…,bi-1,bk,bi,…,bk-1,bk+1,…,bd.对1d,等价于用下列条件代替Lovász条件这个改动似乎改进了规约基的质量,尽管理论上也没有得到可证明的最短矢量界,而且运行时间也可能是亚指数的,但这个方法在实际中运行良好.
Gama和Nguyen用NTL库[18]实现三个不同算法:LLL算法,深插入的LLL算法,分块KZ规约法,实验证实,后两种算法得到规约基质量比LLL要好,而且分块值k越大,得到的规约基的质量越高,但同时运行时间也在增加.
可以看出,这两大类算法是互补的,所有的精确算法首先都用一个近似算法(如LLL)做预处理,而所有的分块算法都要调用许多低维格的精确算法作为子过程.启发式的方法在实际中被大量采用,它们的运行时间提高很多,但理论上仍未得到证明.实际上,在高维时(n≥150),只有近似算法是实用的.
最后,人们以前普遍感觉格基规约算法的实际执行效率比它们可证明的理论界更好.在上世纪80年代末,格问题的计算复杂性吸引了人们的关注,主要因为Ajtai发现某种格近似问题在最坏情况复杂度和平均情况下的复杂度之间联系,吸引了理论密码学和计算机复杂性领域专家的兴趣.
众所周知,密码学需要平均意义上是困难的的问题.当一个密钥被随机选择时,相应的解密函数难于以很高概率被破解.格问题的复杂性打开了密码设计之门.格规约在密码分析上的成功使得人们相信存在象随机Oracle预言器(证明密码安全性的一种理想计算模型)一样强的格基规约算法,但随着Ajtai的最坏/平均情况复杂性格困难问题的证明[19],以及基于格的密码系统NTRU的开发[20],人们对基于格的密码的安全性有了更深的认识.
4 规约算法性能分析
著名的LLL[13]及其变形在多项式时间内计算一个近似因子为的格矢量.对于SVP问题,kannan确定性算法[5]有一个超指数复杂度,需要2O(dlogd)次运算(d指格的维数).Ajtai的随机算法[8]有一个指数复杂度2O(d).
最好的解近似SVP问题的多项式时间算法是分块算法,在每一个小分块上运行精确的SVP算法,比如k是分块大小,当k比较小时,开销仍然是格的维数d的多项式,例如,kannan算法[5],若选择k=log d/log log d,运行时间2O(klogk)仍然是d的多项式.
Gama-Nguyen提出了一个很好的分块算法[17],在多项式次调用一个维数小于等于k的子过程SVP-Oracle后能解近似因子((1+ε的近似SVP问题.
如果取分块大小k=log d,用AKS算法[8] 作为一个SVP子过程,获得一个随机多项式时间算法,解近似因子为,即亚指数因子的格问题.
继Lovász之后,kannan提出了一个求KZ规约基的算法,Kannan的算法[21]返回一个最短格矢量,但需要指数运行时间.
通过运用Kannan算法到长为2k的分块的格基中,Schnorr[15]改进了LLL的近似因子为(k/3)n/k,具有时间复杂度为O(n3kk+O(k)A)(其中A为O(n2)比特长的整数进行算术运算所需的比特运算的数量).
LLL算法是众多规约算法的基础,为了更好地洞察LLL算法的基本思想,我们着重从基B的几何标准型GNF:R=[ri,j] ∈Rn×n来描述标准的LLL规约:格基B=QR∈Rn×n是大小规约的,如果对所有的j>i,|ri,j|/+ε(常忽略ε).
对δ∈(η2,1] ,η=+ε,如果B是大小规约的,且满足条件:
定理4 对α=1/(δ-η2),格L的一个LLL规约基B∈Rn×n满足:
(1)‖b1‖2≤
格基B=QB是HKZ规约(或HKZ基)定义:如果B是大小约简的,且GNF标准型:R=[ri,j] ∈Rn×n的每个对角元系数ri,i在所有GLn(Z)(GLn(Z)={T∈Zn×n|det(T)=±1})变换下是最小的,该变换保持b1,…,bi-1不变.
设基b1,…,bn∈Zn,维数n=k·m,QR分解为[b1,…,bn] =QR,R∈Rn×n.分基矩阵为m个片段Bl=[bk(l-1)+1,…,bkl] ,l=1,…,m.两个相连的片段的局部规约用2k×2k子矩阵Rl:=[rkl+i,kl+j] ,-k<i,j<k∈R2k×2k来表示,其中R2k×2k是R子矩阵,对应于两个相继的片段Bl-1,Bl.局部规约用Bl的表达,通过计算系数ukl+i,kl+j和得到.我们在某个Rl的局部坐标上做LLL交换和大小规约.
在所有的局部LLL规约完成后做额外的全局变换.k-分片规约基目的是最小化这些全局开销.用D(l)=…‖表示分片Bl的局部Gramian行列式.我们有Dkl=D(1)…D(l).
定义10[14]称有序基b1,…,bn∈Zn,n=k·m为δ∈[1/4,1] 的k-分片规约基.如果是大小约简的且对α=1/(δ-1/4)满足:δ‖≤+‖,imod k;
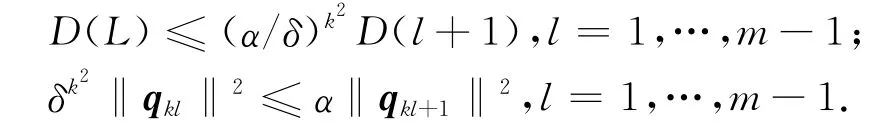
定理5 设b1,…,bn是一个有参数δ的k-分片规约基,则对i=1,…,n:
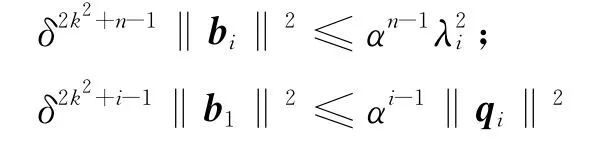
其中λ1≤…≤λn是格的逐次最小值.
k-分片规约算法通过在两个相邻的分片[Bl-1,Bl] =[bk(l-1)+1,…,bkl+k] 上迭代地做局部LLL子过程:Loc-LLL(l).Loc-LLL(l)子程序计算分片[Bl-1,Bl] 的正交化和大小约简.两个相连基矢量的LLL交换及局部大小规约仅仅需要O(k2)算术步,比起全局坐标上的LLL交换的开销O(n2)要少多了.
Koy[14]的原-对偶基(Primal-dual)方法减少运行时间到n3kk/2+O(k)A且仍能达到一个近似因子≤(k/6)k/n.Koy的primal-dual规约减少Dl=如下.最大化RlTl的GNF中的rkl,kl,最小化Rl+1Tl+1的GNF中的rkl+1,kl+1,其中Tl,Tl+1∈GLk(Z),如果能减少rkl,kl和Dl就交换bkl,bkl+1.该算法是分块2k算法变形,被广泛应用在实际中,虽然未被证明是多项式时间的.
Schnorr层次规约法(Hierarchy lattice basis reduction).1987年Schnorr提出了多项式时间的层次规约算法[4].扩展了LLL和KZ规约的技术,改进了Kannan的KZ规约算法.设任意秩为n的格基b1,…,bn∈Rm,该算法作用在O(nlog‖B‖)比特的整数上,能够在O(n2)(+n2)log‖B‖时间内找到一个非零格矢量b,且‖b‖2≤(6k2)k/nλ(L)2,其中k为相应的KZ规约法中基分组长,‖B‖为输入基的最大欧几里得范数.
2001年Ajtai等发现了一个随机算法AKS[8],该算法用了筛法的原理,比kannan的确定性算法具有更好的渐近复杂度.AKS算法以很高的概率在2O(n)时间内找到一个最短格矢量.
文献[22] 提出一种更快的LLL类算法:SLLL算法,用基的分片方式进行,通过迭代子分片进行LLL规约,子分片运行O(n3logn)算术步,最后得到的逐次最小值和原LLL几乎相同.
对维数为n的整格,给定基长度为2O(n),对δ>0,SLLL规约运行在O(n5+ε)比特的整数上,而原LLL运行在O(n7+ε)比特整数上,Schnorr在1988年改进的LLL和Storjohann在1996年实现的LLL需要运行在O(n6+ε)比特整数上.
文献[23] 利用Grover量子搜索算法QSR,能达到近似因子(k/6)n/2k,有预期的运行时间O(n3(k/6)k/8A+n4A),这大约是Schnorr随机抽样规约算法的平方根.量子计算的使用将不仅影响基于整数分解或离散对数问题的密码安全性,而且也影响基于格密码系统的密码安全性,如果目前量子计算机可利用,建议NTRU安全参数需要增加为503-1277.最后给出一个表格进行总结.

表1 几种规约算法的渐近资源界和近似因子
[1] Nguyen P,Vallée B.The LLL algorithm:survey and applications[M] .New York:Springer-Verlag Inc,2010.
[2] Nguyen P,StehléD.Low-dimensional lattice basis reduction revisited(Extended Abstract)[J] .Lecture Notes in Computer Science,2004,3076:338-357,.
[3] Lagarias J,Lenstra H,Schnorr C.Korkin-Zolotarev bases and successive minima of a lattice and its reciprocal lattice[J] .Combinatorica,Springer,1990,10:333-348.
[4] Schnorr C.A hierarchy of polynomial time lattice basis reduction algorithms[J] .Theoretical computer science,Elsevier,1987,53(2-3):201-224.
[5] Kannan R.Improved algorithms for integer programming and related lattice problems[C] //Proceedings of the fifteenth annual ACM symposium on Theory of computing,1983:193-206.
[6] Hanrot G,StehléD.Improved analysis of Kannan’s shortest lattice vector algorithm[C] //Advances in Cryptology-CRYPTO 2007,Springer,2007:170-186.
[7] Schnorr C,Euchner M.Lattice basis reduction:improved practical algorithms and solving subset sum problems[J] .Mathematical programming,Springer,1994,66(1):181-199.
[8] Ajtai M,Kumar R,Sivakumar D.A sieve algorithm for the shortest lattice vector problem[C] //Proceedings of the thirtythird annual ACM symposium on Theory of computing,2001:601-610.
[9] Micciancio D,Voulgaris P.A deterministic single exponential time algorithm for most lattice problems based on voronoi cell computations[C] //Proceedings of the 42nd ACM symposium on Theory of computing,2010:351-358.
[10] Nguyen P,Vidick T.Sieve algorithms for the shortest vector problem are practical[J] .J.of Mathematical Cryptology,Citeseer,2008,2(2):181-207.
[11] Micciancio D,Voulgaris P.Faster exponential time algorithms for the shortest vector problem[C] //Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms,2010:1 468-1 480.
[12] Wang X,Liu M.Improved Nguyen-Vidick heuristic sieve algorithm for shortest vector problem[C] //Proceedings of the 6th ACM Symposium on Information,Computer and Communications Security,2011:1-9.
[13] Lenstra A,Lenstra H,Lovász L.Factoring polynomials with rational coefficients[J] .Mathematische Annalen,Springer,1982,261(4):515-534.
[14] Koy H,Schnorr C.Segment LLL-reduction of lattice bases[M] .Cryptography and lattices,Springer,2001:67-80.
[15] Schnorr C.A more efficient algorithm for lattice basis reduction[J] .Journal of Algorithms,Elsevier,1988,9(1):47-62.
[16] StehléD.Floating-point LLL:theoretical and practical aspects[M] .The LLL Algorithm,Springer,2010:179-213.
[17] Gama N,Nguyen P.Finding short lattice vectors within mordell's inequality[C] .Proceedings of the 40th annual ACM symposium on Theory of computing,2008:207-216.
[18] Shoup V.Number Theory C++Library(NTL)version 5.4.1[CP/OL] .(2011-08-11)[2011-10-31] http://www.shoup.net/ntl/.
[19] Ajtai M.Generating hard instances of lattice problems(extended abstract)[C] //Proceedings of the twenty-eighth annual ACM symposium on Theory of computing,1996:99-108.
[20] Hoffstein J,Pipher J.NTRU:A ring-based public key cryptosystem[M] .Algorithmic number theory,Springer,1998:267.
[21] Kannan R.Minkowski's convex body theorem and integer programming[M] .Mathematics of operations research,JSTOR,1987:415-440.
[22] Schnorr C.Fast LLL-type lattice reduction[J] .Information and Computation,Elsevier,2006,204(1):1-25.
[23] Ludwig C.A faster lattice reduction method using quantum search[M] .Algorithms and Computation,Springer,2003:199-208.

