非均布压力下的减振器节流阀片应力解析计算

李红艳，周长城，高炳凯

（1．山东理工大学交通与车辆工程学院，山东淄博255091；2．淄博市交通监察支队，山东淄博255086）

车辆减振器中应用最多的筒式减振器［1－2]，能有效地衰减簧上和簧下质量的振动，提高车辆行驶平顺性和操纵稳定性［3－4]．减振器阻尼特性主要是由减振器阀系参数所决定的，其中节流阀片厚度对减振器特性起着关键性作用．目前，国内外对减振器阀系参数设计还没有准确、可靠的设计方法［5]，大都是利用经验首先确定一个阀片厚度，然后经过反复试验和修改，最后才确定出所设计参数，其主要原因是目前国内外缺乏可靠的减振器设计理论，对阀片在非均布载荷下变形和应力计算还没有可靠的解析计算式，大都是利用文献［6] 对阀片最大挠度和应力进行近似计算．尽管我国已有学者对此进行了大量研究，建立了均布压力下的变形和应力解析计算方法［7]，并对非均布线性压力下的减振器节流阀片变形进行了研究，给出了解析计算式［8]，然而，对于在非均布压力下的应力尚未给出解析计算式．因此，目前节流阀片应力的解析计算方法，不能满足减振器节流阀片厚度设计和应力强度分析的要求，还必须解决节流阀片在非均布压力下的应力解析计算问题．

本文以某减振器环形节流弹性阀片为例，建立减振器节流阀片非均布载荷力学模型，对应力解析计算进行研究，建立在非均布载荷下的节流阀片应力解析计算式，通过实例对节流阀片在非均布压力下的应力进行解析计算，并利用ANSYS软件进行数值仿真验证．

1 阀片非均布压力力学模型

如图1所示，减振器环形弹性节流阀片中间是固定约束，有效内圆半径为ra，外圆半径为rb，阀片厚度为h．考虑减振器节流阀口半径rk位置处的常通节流孔和环型节流缝隙，节流阀片所受的压力为非均布压力，即在［ra，rk] 范围内的压力为p0，而［rk，rb] 范围内为线性非均布递减压力．

图1 节流阀片力学模型

阀片所受非均布压力绕z轴对称，当阀口半径为rk时，阀片所受的非均布压力可表示为

因此，节流阀片所受力为非均布压力时，可看作在［ra，rb] 区间上均布压力p0与［rk，rb] 区间上的线性非均布压力的叠加，如图2所示．

图2 非均布压力叠加示意图

2 阀片在非均布压力下的变形

2．1 均布压力下的阀片变形

根据弯曲变形系数法［9]，在均布压力p0作用下，厚度为h的环型节流阀片在任意半径r处的变形frU可表示为

式中，GrU为环型节流阀片在均布压力p0作用下，在半径r位置处的变形系数（单位为m6·N－1），它与阀片结构、弹性模量、泊松比和半径r有关；frU为阀片在均布压力p0作用下，在半径r处的变形量．

2．2 线性非均布压力下的阀片变形

2．2．1 阀片变形曲面方程

由图2可知，节流阀片所受线性非均布压力可表示为

由于阀片结构和所受载荷都是关于z轴对称的，根据弹性力学可得在线性作用下，节流阀片线性非均布压力作用下的变形曲面微分方程为［10]

2．2．2 曲面方程的解

将（3）式代入（4）式，可得微分方程（4）的通解为

和C1，C2，C3，C4共8个常数，可由节流阀片在内圆和外圆处的边界条件，以及半径rk处的连续性条件所确定，即

①内圆处的变形等于零，即frN1＝0，根据阀片变形曲面的通解（3）可得

②内圆处的变形斜率等于零，即

可得

③外圆处的力矩等于零，即M｜r＝rb＝0，可得

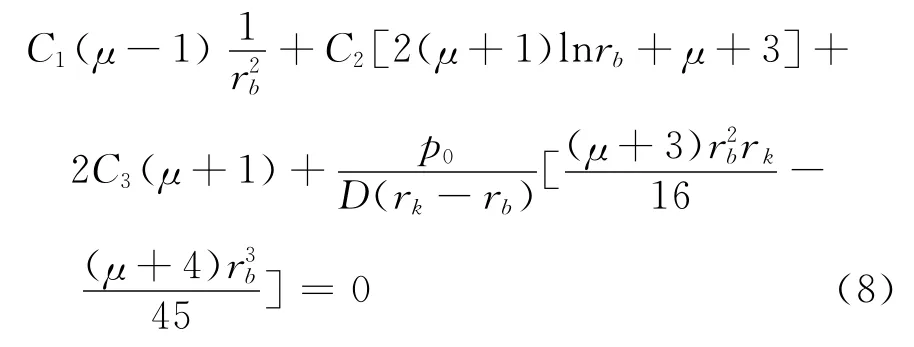
④外圆处的剪切力等于零，即Q｜r＝rb＝0，因此

可得

⑤阀片半径rk处的变形连续，即frN1＝frN2，可得

⑥阀片半径rk处的变形斜率相等，即

可得

⑦阀片半径rk处的弯矩相等，M1｜r＝rk＝M2，可得

⑧阀片半径rk处的剪切力相等，即Q1＝，可得

通过联立式（6）～（13），可求得环形节流阀片在线性非均布载荷作用下的弯曲变形微分方程通解的8个常数，即B1，B2，B3，B4和C1，C2，C3，C4，从而得到在线性非均布载荷下阀片弯曲变形通解表达式．

2．2．3 阀片变形解析计算式

根据上述边界条件和连续性条件，可得8个参数，将8个常数代入阀片变形曲面微分方程的通解（5），便可得到在线性非均布压力下，节流阀片在任意半径位置的变形解析式．分析可知，阀片变形解的各项都含有一个公因子p0／h3，对式（5）提取公因子p0／h3，将剩余项归结为一个常数GrN，即阀片在半径r位置处的变形系数，则阀片在半径r处的变形量可表达为

式中，GrN即为阀片在线性非均布压力作用下，在半径r处的变形系数，它不仅与阀片的结构、弹性模量、泊松比、半径位置有关，还与线性非均布载荷的加载位置有关．

2．3 阀片在非均布压力下的叠加变形

阀片在非均布压力下的变形，可看作是均布压力和线性非均布压力下变形的叠加．因此，由（2）式和（14）式得，节流阀片在非均布压力下的变形fr为

式中，Gr为节流阀片在非均布压力作用下，在半径r处的变形系数，等于均布变形系数与线性非均布变形系数的叠加．

因此，只要求得在非均布压力下半径位置处的变形系数Gr，便可求得节流阀片在对应半径r处的变形量fr．

3 非均布压力下的阀片应力

3．1 阀片内力

减振器环形节流阀片所受的内力主要是径向弯矩Mr和周向弯矩Mθ，根据弹性力学原理，节流阀片所受内力Mr和Mθ可分别表示为

将（16）式代入（17）式和（18）式，可得

3．2 阀片应力

根据弹性力学原理可知，阀片在半径r位置上、下表面（z＝±h／2，z为阀片轴向位置坐标）处的应力最大．由应力与内力之间的关系，可得阀片上、下表面上的径向应力和周向应力分别为

将（19）式和（20）式分别代入（21）式和（22）式，可得

Gσθ，则（23）式和（24）式可表示为

式中，Gσr和Gσθ分别为所定义阀片的径向应力系数和周向应力系数，其物理意义分别为阀口半径rk处的单位厚度阀片，在单位最大非均布压力作用下，阀片上、下表面在位置半径r处的径向和周向应力的大小，单位为m2或mm2．

根据第四强度理论，阀片所受的复合应力为

将（25）和（26）式代入（27）式，可得

如某环型节流阀片的内半径ra＝5．0mm，外半径rb＝8．5mm，阀口半径rk＝8．0mm，弹性模量E＝200GPa，泊松比μ＝0．3，在线性非均布载荷作用下，阀片应力系数随半径r的变化情况如图3所示．

图3 阀片应力系数随半径γ变化曲线

因此，只要求得阀片在任意半径r处的径向、周向和复合应力系数，便可分别利用（25）式、（26）式和（27）式，解析计算在非均布压力作用下的节流阀片在任意半径r位置处的径向应力σr、周向应力σθ和复合应力σcom．

4 阀片应力解析计算实例

4．1 阀片各向应力计算

对于上述环型节流阀片，阀片厚度h＝0．3mm在最大非均布压力p0＝3MPa作用下，利用（25）、（26）和（28）式，分别解析计算可得到阀片的径向应力、周向应力和复合应力，结果如图4所示．

图4 阀片在非均布压力下的应力

阀片在不同半径r处的径向应力、周向应力和复合应力的解析计算值见表1．

表1 阀片各向应力解析计算值

4．2 阀片在不同阀口半径下的应力

对于上述环形节流阀片，在最大非均布压力p0＝3MPa时，当阀口半径rk＝6．5mm，rk＝7．0mm，rk＝7．5mm和rk＝8．0mm情况下，利用利用（25），（26）和（27）式，可分别解析计算阀片在任意半径位置的径向应力、周向应力和复合应力．其中，在不同阀口半径下，阀片复合应力随半径变化情况如图5所示．

图5 不同阀口半径下阀片复合应力

不同阀口半径下，节流阀片在不同半径位置处的复合应力解析计算结果见表2．

表2 不同阀口半径下阀片复合应力σcom解析计算值 MPa

4．3 阀片在不同最大非均布压力作用下的应力

在阀口半径相同情况下，阀片应力将随最大非均布压力的不同而变化．对于上述环形节流阀片，减振器阀口半径rk＝8．0mm时，在最大非均布压力分别为3．0MPa、2．0MPa和1．0MPa情况下的阀片复合应力如图6所示．

图6 阀片在不同非均布压力下的复合应力

阀片在不同最大非均布压力下的复合应力解析计算结果见表3．

表3 不同非均布压力下阀片复合应力σcom解析计算值 MPa

5 数值仿真验证

对于上述节流阀片，利用ANSYS有限元分析软件建立模型，其边界约束条件与图1的力学模型一致，以0．1mm为单位对模型划分网格，施加非均布载荷如图1所示，其中，在［5．0，8．0] mm区间内施加均布压力3．0MPa，而在半径［8．0，8．5] mm区间内施加线性递减压力，然后进行静力学应力仿真分析，仿真结果如图7所示．

由图7可知，利用ANSYS有限元仿真分析软件，对阀片进行应力仿真分析所得到的最大应力为1 186MPa，与表3中解析计算得到的最大应力1202．7MPa基本吻合，相对偏差仅为1．41%．仿真验证结果表明，节流阀片在非均布压力作用下的应力叠加解析计算方法是正确的．

图7 阀片应力仿真云图

6 结论

通过对减振器节流阀片在非均布载荷作用下的应力解析计算与仿真验证可知：

（1）节流阀片在非均布压力下的变形，可看作是在均布压力和线性非均布压力作用下的阀片变形的叠加．

（2）节流阀片在线性非均布压力下的弯曲变形通解中的8个常数，可利用阀片的边界约束条件和变形连续性条件加以确定．

（3）利用阀片变形、内力和应力之间的关系，可得到在非均布压力下，阀片在任意半径r处的径向、周向和复合应力解析计算式．

（4）利用阀片应力系数法，可解析计算在非均布压力作用下，阀片在任意位置半径r处的径向、周向和复合应力．

（5）解析计算得到的节流阀片应力与利用有限元仿真分析软件所得到的仿真值吻合，说明所建立的在非均布压力作用下的节流阀片应力解析计算方法是正确、可靠的．

［1] 李世民，吕振华．汽车筒式液阻减振器技术的发展［J] ．汽车技术，2001，32（8）：10－16．

［2] 陈勇，何辉，白金福．夏利轿车液力油气弹簧簧片的变形分析［J] ．汽车技术，2000，31（1）：19－21．

［3] 陈龙，汪若尘，江浩斌．基于大系统理论半主动悬架系统［J] ．机械工程学报，2008，44（8）：97－101．

［4] 周长城，顾亮．筒式减振器叠加节流阀片开度与特性试验［J] ．机械工程学报，2007，43（6）：210－215．

［5] 姚嘉伶，蔡伟义，陈宁．汽车半主动悬架系统发展状况［J] ．汽车工程，2006，28（3）：276－280．

［6] 成大先．机械设计手册［M] ．北京：化学工业出版社，1996．

［7] 周长城，石佩林．油气弹簧节流阀片应力分析［J] ．汽车工程，2008，30（4）：349－353．

［8] 蔡艳辉，周长城．线性非均布压力下减振器环形阀片变形解析计算［J] ，农业装备与车辆工程，2009（10）：24－27．

［9] 周长城，顾亮，王丽．节流阀片弯曲变形与变形系数［J] ．北京理工大学学报：自然科学版，2006，26（7）：581－584．

［10] 徐芝纶．弹性力学［M] ．北京：高等教育出版社，1990．